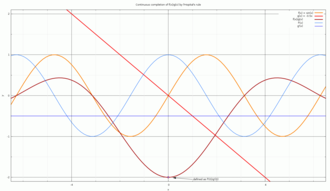
ตัวอย่างการประยุกต์ใช้ของกฎของโลปีตาล เมื่อ
f
(
x
)
=
sin
(
x
)
{\displaystyle {\color {orange}f(x)}=\color {orange}\sin(x)}
g
(
x
)
=
−
0.5
x
{\displaystyle {\color {red}g(x)}=\color {red}-0.5x}
h
(
x
)
=
f
(
x
)
/
g
(
x
)
{\displaystyle {\color {brown}h(x)}={\color {orange}f(x)}/{\color {red}g(x)}}
x = 0
R
{\displaystyle \mathbb {R} }
h
(
0
)
=
f
′
(
0
)
/
g
′
(
0
)
=
−
2
{\displaystyle {\color {brown}h(0)}={\color {teal}f'(0)}/{\color {blue}g'(0)}=-2}
ในแคลคูลัส กฎของโลปีตาล (อังกฤษ : L'Hôpital's rule) หรือ กฎของแบร์นูลลี (อังกฤษ : ฺBernoulli's rule) เป็นทฤษฎีบทคณิตศาสตร์ที่ว่าด้วยการหาค่าลิมิต ที่อยู่ในรูปแบบยังไม่กำหนด (อังกฤษ : indeterminate forms) ด้วยการใช้อนุพันธ์ กฎนี้มักนำมาใช้ในการเปลี่ยนรูปแบบยังไม่กำหนด เป็นรูปแบบกำหนด เพื่อให้ง่ายต่อการคำนวณลิมิตโดยการแทนค่าเข้าไปตรง ๆ กฎนี้ถูกตั้งชื่อตามนักคณิตศาสตร์ ชาวฝรั่งเศส กีโยม เดอ โลปีตาล ถึงแม้กฎนี้มักถูกพิจารณาว่าถูกเขียนโดยเดอ โลปีตาล แต่ทฤษฎีบทนี้แบร์นูลลีเป็นคนเสนอให้กับเขา
กีโยม เดอ โลปีตาล เผยแพร่กฎนี้ในปีพ.ศ.2239 (ค.ศ.1696) ในหนังสือชื่อ Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes แคลคูลัสเชิงอนุพันธ์ [ 1] โยฮันน์ แบร์นูลลี [ 2]
รูปทั่วไปของกฎของโลปีตาลครอบคลุมหลากหลายกรณี ให้
c
{\displaystyle c}
L
{\displaystyle L}
จำนวนจริงส่วนขยาย (ต.ย. จำนวนจริง อนันต์บวก อนันต์ลบ) ให้
I
{\displaystyle I}
ช่วงเปิด ที่มี
c
{\displaystyle c}
c
{\displaystyle c}
ลิมิตข้างเดียว หรือลิมิตที่อนันต์ ถ้า
c
{\displaystyle c}
f
{\displaystyle f}
g
{\displaystyle g}
หาอนุพันธ์ได้ บน
I
{\displaystyle I}
c
{\displaystyle c}
g
′
(
x
)
≠
0
{\displaystyle g'(x)\neq 0}
I
{\displaystyle I}
c
{\displaystyle c}
lim
x
→
c
f
′
(
x
)
g
′
(
x
)
=
L
{\textstyle \lim \limits _{x\to c}{\frac {f'(x)}{g'(x)}}=L}
x
{\displaystyle x}
c
{\displaystyle c}
ถ้า
lim
x
→
c
f
(
x
)
=
lim
x
→
c
g
(
x
)
=
0
{\displaystyle \lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0}
หรือ
lim
x
→
c
|
f
(
x
)
|
=
lim
x
→
c
|
g
(
x
)
|
=
∞
{\displaystyle \lim _{x\to c}|f(x)|=\lim _{x\to c}|g(x)|=\infty }
อย่างใดอย่างหนึ่งแล้ว
lim
x
→
c
f
(
x
)
g
(
x
)
=
L
{\displaystyle \lim _{x\to c}{f(x) \over g(x)}=L}
ถึงแม้ว่าเราจะเขียนในรูป
x
→
c
{\displaystyle x\to c}
x
→
c
+
{\displaystyle x\to c^{+}}
x
→
c
−
{\displaystyle x\to c^{-}}
c
{\displaystyle c}
I
{\displaystyle I}
ในกรณีที่สองนั้น สมมุติฐานให้
f
{\displaystyle f}
ลู่ออก ไปอนันต์จะไม่ได้ถูกใช้ในบทพิสูจน์ (ดูหมายเหตุตรงท้ายหัวเรื่องบทพิสูจน์ ) ดั้งนั้นโดยปกติเงื่อนไขของกฎจะกล่าวไว้ตามข้างบน เงื่อนไขที่เพียงพอที่สองที่จะทำให้กระบวนการของกฎนี้ถูกต้องสามารถกล่าวได้อย่างสั้น ๆ ว่า
lim
x
→
c
|
g
(
x
)
|
=
∞
{\textstyle \lim _{x\to c}|g(x)|=\infty }
สมมุติฐานที่ว่า
g
′
(
x
)
≠
0
{\displaystyle g'(x)\neq 0}
[ 3]
I
{\displaystyle I}
c
{\displaystyle c}
[ 4]
f
{\displaystyle f}
g
{\displaystyle g}
c
{\displaystyle c}
ตัวอย่างพื้นฐานที่มีฟังก์ชันเลขชี้กำลัง ในรูปแบบยังไม่กำหนด
0
0
{\displaystyle {\frac {0}{0}}}
x
=
0
{\displaystyle x=0}
lim
x
→
0
e
x
−
1
x
2
+
x
=
lim
x
→
0
d
d
x
(
e
x
−
1
)
d
d
x
(
x
2
+
x
)
=
lim
x
→
0
e
x
2
x
+
1
=
1
{\displaystyle {\begin{aligned}\lim _{x\to 0}{\frac {e^{x}-1}{x^{2}+x}}&=\lim _{x\to 0}{\frac {{\frac {d}{dx}}(e^{x}-1)}{{\frac {d}{dx}}(x^{2}+x)}}\\[4pt]&=\lim _{x\to 0}{\frac {e^{x}}{2x+1}}\\[4pt]&=1\end{aligned}}}
ตัวอย่างที่ซับซ้อนขึ้นที่เป็น
0
0
{\textstyle {\frac {0}{0}}}
lim
x
→
0
2
sin
(
x
)
−
sin
(
2
x
)
x
−
sin
(
x
)
=
lim
x
→
0
2
cos
(
x
)
−
2
cos
(
2
x
)
1
−
cos
(
x
)
=
lim
x
→
0
−
2
sin
(
x
)
+
4
sin
(
2
x
)
sin
(
x
)
=
lim
x
→
0
−
2
cos
(
x
)
+
8
cos
(
2
x
)
cos
(
x
)
=
−
2
+
8
1
=
6
{\displaystyle {\begin{aligned}\lim _{x\to 0}{\frac {2\sin(x)-\sin(2x)}{x-\sin(x)}}&=\lim _{x\to 0}{\frac {2\cos(x)-2\cos(2x)}{1-\cos(x)}}\\[4pt]&=\lim _{x\to 0}{\frac {-2\sin(x)+4\sin(2x)}{\sin(x)}}\\[4pt]&=\lim _{x\to 0}{\frac {-2\cos(x)+8\cos(2x)}{\cos(x)}}\\[4pt]&={\frac {-2+8}{1}}\\[4pt]&=6\end{aligned}}}
ตัวอย่างที่เป็น
∞
∞
{\textstyle {\frac {\infty }{\infty }}}
lim
x
→
∞
x
n
e
x
=
lim
x
→
∞
n
x
n
−
1
e
x
=
n
⋅
lim
x
→
∞
x
n
−
1
e
x
{\displaystyle \lim _{x\to \infty }{\frac {x^{n}}{e^{x}}}=\lim _{x\to \infty }{\frac {nx^{n-1}}{e^{x}}}=n\cdot \lim _{x\to \infty }{\frac {x^{n-1}}{e^{x}}}}
n
{\displaystyle n}
n
{\displaystyle n}
ตัวอย่างที่เป็นรูปแบบยังไม่กำหนด
0
⋅
∞
{\displaystyle 0\cdot \infty }
∞
∞
{\displaystyle {\frac {\infty }{\infty }}}
lim
x
→
0
+
x
ln
x
=
lim
x
→
0
+
ln
x
1
x
=
lim
x
→
0
+
1
x
−
1
x
2
=
lim
x
→
0
+
−
x
=
0.
{\displaystyle \lim _{x\to 0^{+}}x\ln x=\lim _{x\to 0^{+}}{\frac {\ln x}{\frac {1}{x}}}=\lim _{x\to 0^{+}}{\frac {\frac {1}{x}}{-{\frac {1}{x^{2}}}}}=\lim _{x\to 0^{+}}-x=0.}
สามารถใช้กฎของโลปีตาลในการพิสูจน์ทฤษฎีบทที่ว่า ถ้า
f
{\displaystyle f}
x
{\displaystyle x}
lim
h
→
0
f
(
x
+
h
)
+
f
(
x
−
h
)
−
2
f
(
x
)
h
2
=
lim
h
→
0
f
′
(
x
+
h
)
−
f
′
(
x
−
h
)
2
h
=
lim
h
→
0
f
″
(
x
+
h
)
+
f
″
(
x
−
h
)
2
=
f
″
(
x
)
{\displaystyle {\begin{aligned}\lim _{h\to 0}{\frac {f(x+h)+f(x-h)-2f(x)}{h^{2}}}&=\lim _{h\to 0}{\frac {f'(x+h)-f'(x-h)}{2h}}\\[4pt]&=\lim _{h\to 0}{\frac {f''(x+h)+f''(x-h)}{2}}\\[4pt]&=f''(x)\end{aligned}}}
บางครั้งมีวิธีพลิกแพลงที่ใช้กฎของโลปีตาล เช่นสมมติให้
f
(
x
)
+
f
′
(
x
)
{\displaystyle f(x)+f'(x)}
x
→
∞
{\displaystyle x\to \infty }
e
x
⋅
f
(
x
)
{\displaystyle e^{x}\cdot f(x)}
lim
x
→
∞
f
(
x
)
=
lim
x
→
∞
e
x
⋅
f
(
x
)
e
x
=
lim
x
→
∞
e
x
(
f
(
x
)
+
f
′
(
x
)
)
e
x
=
lim
x
→
∞
(
f
(
x
)
+
f
′
(
x
)
)
{\displaystyle \lim _{x\to \infty }f(x)=\lim _{x\to \infty }{\frac {e^{x}\cdot f(x)}{e^{x}}}=\lim _{x\to \infty }{\frac {e^{x}{\bigl (}f(x)+f'(x){\bigr )}}{e^{x}}}=\lim _{x\to \infty }{\bigl (}f(x)+f'(x){\bigr )}}
lim
x
→
∞
f
(
x
)
{\textstyle \lim _{x\to \infty }f(x)}
lim
x
→
∞
f
′
(
x
)
=
0
{\textstyle \lim _{x\to \infty }f'(x)=0}
[ แก้ ] รูปแบบยังไม่กำหนดอื่น ๆ เช่น
1
∞
{\displaystyle 1^{\infty }}
0
0
{\displaystyle 0^{0}}
∞
0
{\displaystyle \infty ^{0}}
0
⋅
∞
{\displaystyle 0\cdot \infty }
∞
−
∞
{\displaystyle \infty -\infty }
∞
−
∞
{\displaystyle \infty -\infty }
lim
x
→
1
(
x
x
−
1
−
1
ln
x
)
=
lim
x
→
1
x
⋅
ln
x
−
x
+
1
(
x
−
1
)
⋅
ln
x
(
1
)
=
lim
x
→
1
ln
x
x
−
1
x
+
ln
x
(
2
)
=
lim
x
→
1
x
⋅
ln
x
x
−
1
+
x
⋅
ln
x
(
3
)
=
lim
x
→
1
1
+
ln
x
1
+
1
+
ln
x
(
4
)
=
lim
x
→
1
1
+
ln
x
2
+
ln
x
=
1
2
{\displaystyle {\begin{aligned}\lim _{x\to 1}\left({\frac {x}{x-1}}-{\frac {1}{\ln x}}\right)&=\lim _{x\to 1}{\frac {x\cdot \ln x-x+1}{(x-1)\cdot \ln x}}&\quad (1)\\[6pt]&=\lim _{x\to 1}{\frac {\ln x}{{\frac {x-1}{x}}+\ln x}}&\quad (2)\\[6pt]&=\lim _{x\to 1}{\frac {x\cdot \ln x}{x-1+x\cdot \ln x}}&\quad (3)\\[6pt]&=\lim _{x\to 1}{\frac {1+\ln x}{1+1+\ln x}}&\quad (4)\\[6pt]&=\lim _{x\to 1}{\frac {1+\ln x}{2+\ln x}}\\[6pt]&={\frac {1}{2}}\\\end{aligned}}}
กฎของโลปีตาลถูกใช้ในขั้นตอนจาก (1) ไป (2) และอีกครั้งในขั้นตอน (3) ไป (4)
กฎของโลปีตาลใช้ได้กับรูปแบบยังไม่กำหนดที่มีเลขยกกำลัง โดยใช้ลอการิทึม ช่วย"ตบเลขยกกำลังลงมา" ตัวอย่างเช่น
lim
x
→
0
+
x
x
=
lim
x
→
0
+
e
ln
(
x
x
)
=
lim
x
→
0
+
e
x
⋅
ln
x
=
e
lim
x
→
0
+
(
x
⋅
ln
x
)
{\displaystyle \lim _{x\to 0^{+}}x^{x}=\lim _{x\to 0^{+}}e^{\ln(x^{x})}=\lim _{x\to 0^{+}}e^{x\cdot \ln x}=e^{\lim \limits _{x\to 0^{+}}(x\cdot \ln x)}}
ย้ายลิมิตเข้าไปในฟังก์ชันเลขชี้กำลัง ได้เพราะฟังก์ชันเลขชี้กำลังเป็นฟังก์ชันต่อเนื่อง และการที่เลขชี้กำลัง
x
{\displaystyle x}
lim
x
→
0
+
x
⋅
ln
x
{\displaystyle \lim _{x\to 0^{+}}x\cdot \ln x}
0
⋅
∞
{\displaystyle 0\cdot \infty }
lim
x
→
0
+
x
⋅
ln
x
=
0
{\displaystyle \lim _{x\to 0^{+}}x\cdot \ln x=0}
lim
x
→
0
+
x
x
=
e
0
=
1
{\displaystyle \lim _{x\to 0^{+}}x^{x}=e^{0}=1}
ตารางต่อไปนี้คือรายการรูปแบบยังไม่กำหนดที่พบบ่อย กับการแปลงโดยใช้กฎโลปีตาล
รูปแบบยังไม่กำหนด
เงื่อนไข
การแปลงเป็น
0
/
0
{\displaystyle 0/0}
0
0
{\displaystyle {\frac {0}{0}}}
lim
x
→
c
f
(
x
)
=
0
,
lim
x
→
c
g
(
x
)
=
0
{\displaystyle \lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=0\!}
—
∞
∞
{\displaystyle {\frac {\infty }{\infty }}}
lim
x
→
c
f
(
x
)
=
∞
,
lim
x
→
c
g
(
x
)
=
∞
{\displaystyle \lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!}
lim
x
→
c
f
(
x
)
g
(
x
)
=
lim
x
→
c
1
/
g
(
x
)
1
/
f
(
x
)
{\displaystyle \lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {1/g(x)}{1/f(x)}}\!}
0
⋅
∞
{\displaystyle 0\cdot \infty }
lim
x
→
c
f
(
x
)
=
0
,
lim
x
→
c
g
(
x
)
=
∞
{\displaystyle \lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=\infty \!}
lim
x
→
c
f
(
x
)
g
(
x
)
=
lim
x
→
c
f
(
x
)
1
/
g
(
x
)
{\displaystyle \lim _{x\to c}f(x)g(x)=\lim _{x\to c}{\frac {f(x)}{1/g(x)}}\!}
∞
−
∞
{\displaystyle \infty -\infty }
lim
x
→
c
f
(
x
)
=
∞
,
lim
x
→
c
g
(
x
)
=
∞
{\displaystyle \lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!}
lim
x
→
c
(
f
(
x
)
−
g
(
x
)
)
=
lim
x
→
c
1
/
g
(
x
)
−
1
/
f
(
x
)
1
/
(
f
(
x
)
g
(
x
)
)
{\displaystyle \lim _{x\to c}(f(x)-g(x))=\lim _{x\to c}{\frac {1/g(x)-1/f(x)}{1/(f(x)g(x))}}\!}
0
0
{\displaystyle 0^{0}}
lim
x
→
c
f
(
x
)
=
0
+
,
lim
x
→
c
g
(
x
)
=
0
{\displaystyle \lim _{x\to c}f(x)=0^{+},\lim _{x\to c}g(x)=0\!}
lim
x
→
c
f
(
x
)
g
(
x
)
=
exp
lim
x
→
c
g
(
x
)
1
/
ln
f
(
x
)
{\displaystyle \lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!}
1
∞
{\displaystyle 1^{\infty }}
lim
x
→
c
f
(
x
)
=
1
,
lim
x
→
c
g
(
x
)
=
∞
{\displaystyle \lim _{x\to c}f(x)=1,\ \lim _{x\to c}g(x)=\infty \!}
lim
x
→
c
f
(
x
)
g
(
x
)
=
exp
lim
x
→
c
ln
f
(
x
)
1
/
g
(
x
)
{\displaystyle \lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!}
∞
0
{\displaystyle \infty ^{0}}
lim
x
→
c
f
(
x
)
=
∞
,
lim
x
→
c
g
(
x
)
=
0
{\displaystyle \lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=0\!}
lim
x
→
c
f
(
x
)
g
(
x
)
=
exp
lim
x
→
c
g
(
x
)
1
/
ln
f
(
x
)
{\displaystyle \lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!}
การพิสูจน์กฎโลปีตาลนั้นง่ายในกรณีที่
f
{\displaystyle f}
g
{\displaystyle g}
c
{\displaystyle c}
c
{\displaystyle c}
พหุนาม ไซน์ และโคไซน์ ฟังก์ชันเลขชี้กำลัง ) จึงเป็นกรณีที่สมควรแก่การสนใจ
ให้
f
{\displaystyle f}
g
{\displaystyle g}
c
{\displaystyle c}
f
(
c
)
=
g
(
c
)
=
0
{\displaystyle f(c)=g(c)=0}
g
′
(
c
)
≠
0
{\displaystyle g'(c)\neq 0}
lim
x
→
c
f
(
x
)
g
(
x
)
=
lim
x
→
c
f
(
x
)
−
0
g
(
x
)
−
0
=
lim
x
→
c
f
(
x
)
−
f
(
c
)
g
(
x
)
−
g
(
c
)
=
lim
x
→
c
(
f
(
x
)
−
f
(
c
)
x
−
c
)
(
g
(
x
)
−
g
(
c
)
x
−
c
)
=
lim
x
→
c
(
f
(
x
)
−
f
(
c
)
x
−
c
)
lim
x
→
c
(
g
(
x
)
−
g
(
c
)
x
−
c
)
=
f
′
(
c
)
g
′
(
c
)
=
lim
x
→
c
f
′
(
x
)
g
′
(
x
)
{\displaystyle {\begin{aligned}&\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f(x)-0}{g(x)-0}}=\lim _{x\to c}{\frac {f(x)-f(c)}{g(x)-g(c)}}\\[6pt]={}&\lim _{x\to c}{\frac {\left({\frac {f(x)-f(c)}{x-c}}\right)}{\left({\frac {g(x)-g(c)}{x-c}}\right)}}={\frac {\lim \limits _{x\to c}\left({\frac {f(x)-f(c)}{x-c}}\right)}{\lim \limits _{x\to c}\left({\frac {g(x)-g(c)}{x-c}}\right)}}={\frac {f'(c)}{g'(c)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}\end{aligned}}}
c
{\displaystyle c}
g
′
(
c
)
≠
0
{\displaystyle g'(c)\neq 0}
บทพิสูจน์ทั่วไปของกฎโลปีตาลได้รับการอธีบายไว้ข้างล่างนี้
บทพิสูจน์ต่อไปนี้เป็นของเทย์เลอร์ (1952) harvtxt error: no target: CITEREFเทย์เลอร์1952 (help ) ซึ่งพิสูจน์รูปแบบยังไม่กำหนดทั้ง
0
0
{\textstyle {\frac {0}{0}}}
±
∞
±
∞
{\textstyle {\frac {\pm \infty }{\pm \infty }}}
เลตเทินมาเยอร์ (1936) harvtxt error: no target: CITEREFเลตเทินมาเยอร์1936 (help ) และวาเซวสกี (1949) harvtxt error: no target: CITEREFวาเซวสกี1949 (help )
ให้
f
{\displaystyle f}
g
{\displaystyle g}
รูปทั่วไป ให้
I
{\displaystyle {\mathcal {I}}}
c
{\displaystyle c}
g
′
(
x
)
≠
0
{\displaystyle g'(x)\neq 0}
g
{\displaystyle g}
I
{\displaystyle {\mathcal {I}}}
g
{\displaystyle g}
I
{\displaystyle {\mathcal {I}}}
สำหรับทุก
x
{\displaystyle x}
m
(
x
)
=
inf
f
′
(
ξ
)
g
′
(
ξ
)
{\displaystyle m(x)=\inf {\frac {f'(\xi )}{g'(\xi )}}}
M
(
x
)
=
sup
f
′
(
ξ
)
g
′
(
ξ
)
{\displaystyle M(x)=\sup {\frac {f'(\xi )}{g'(\xi )}}}
ξ
{\displaystyle \xi }
x
{\displaystyle x}
c
{\displaystyle c}
inf
{\textstyle \inf }
sup
{\textstyle \sup }
อินฟิมัม กับซูพรีมัม ตามลำดับ)
จากการหาอนุพันธ์ได้ของ
f
{\displaystyle f}
g
{\displaystyle g}
I
{\displaystyle {\mathcal {I}}}
ทฤษฎีบทค่าเฉลี่ยของโคชี ยืนยันได้ว่าสำหรับจุดสองจุดใด ๆ
x
{\displaystyle x}
y
{\displaystyle y}
I
{\displaystyle {\mathcal {I}}}
ξ
{\displaystyle \xi }
x
{\displaystyle x}
y
{\displaystyle y}
f
(
x
)
−
f
(
y
)
g
(
x
)
−
g
(
y
)
=
f
′
(
ξ
)
g
′
(
ξ
)
{\displaystyle {\frac {f(x)-f(y)}{g(x)-g(y)}}={\frac {f'(\xi )}{g'(\xi )}}}
m
(
x
)
≤
f
(
x
)
−
f
(
y
)
g
(
x
)
−
g
(
y
)
≤
M
(
x
)
{\displaystyle m(x)\leq {\frac {f(x)-f(y)}{g(x)-g(y)}}\leq M(x)}
x
{\displaystyle x}
y
{\displaystyle y}
ค่า
g
(
x
)
−
g
(
y
)
{\displaystyle g(x)-g(y)}
x
{\displaystyle x}
y
{\displaystyle y}
ทฤษฎีบทค่าเฉลี่ย จะนิรนัยได้ว่ามี
p
{\displaystyle p}
x
{\displaystyle x}
y
{\displaystyle y}
g
′
(
p
)
=
0
{\displaystyle g'(p)=0}
จากนิยามของ
m
(
x
)
{\displaystyle m(x)}
M
(
x
)
{\displaystyle M(x)}
±
∞
{\textstyle \pm \infty }
m
(
x
)
{\displaystyle m(x)}
M
(
x
)
{\displaystyle M(x)}
f
g
{\textstyle {\frac {f}{g}}}
กรณีที่ 1
lim
x
→
c
f
(
x
)
=
lim
x
→
c
g
(
x
)
=
0
{\displaystyle \lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0}
สำหรับทุก
x
{\displaystyle x}
I
{\displaystyle {\mathcal {I}}}
y
{\displaystyle y}
x
{\displaystyle x}
c
{\displaystyle c}
m
(
x
)
≤
f
(
x
)
−
f
(
y
)
g
(
x
)
−
g
(
y
)
=
f
(
x
)
g
(
x
)
−
f
(
y
)
g
(
x
)
1
−
g
(
y
)
g
(
x
)
≤
M
(
x
)
{\displaystyle m(x)\leq {\frac {f(x)-f(y)}{g(x)-g(y)}}={\frac {{\frac {f(x)}{g(x)}}-{\frac {f(y)}{g(x)}}}{1-{\frac {g(y)}{g(x)}}}}\leq M(x)}
และเมื่อ
y
{\displaystyle y}
c
{\displaystyle c}
f
(
y
)
g
(
x
)
{\displaystyle {\frac {f(y)}{g(x)}}}
g
(
y
)
g
(
x
)
{\displaystyle {\frac {g(y)}{g(x)}}}
m
(
x
)
≤
f
(
x
)
g
(
x
)
≤
M
(
x
)
{\textstyle m(x)\leq {\frac {f(x)}{g(x)}}\leq M(x)}
กรณีที่ 2
lim
x
→
c
|
g
(
x
)
|
=
∞
{\displaystyle \lim _{x\to c}|g(x)|=\infty }
สำหรับทุก
x
{\displaystyle x}
I
{\displaystyle {\mathcal {I}}}
S
x
=
{
y
∣
y
{\displaystyle S_{x}=\{y\mid y}
x
{\displaystyle x}
c
}
{\displaystyle c\}}
y
{\displaystyle y}
x
{\displaystyle x}
c
{\displaystyle c}
m
(
x
)
≤
f
(
y
)
−
f
(
x
)
g
(
y
)
−
g
(
x
)
=
f
(
y
)
g
(
y
)
−
f
(
x
)
g
(
y
)
1
−
g
(
x
)
g
(
y
)
≤
M
(
x
)
{\displaystyle m(x)\leq {\frac {f(y)-f(x)}{g(y)-g(x)}}={\frac {{\frac {f(y)}{g(y)}}-{\frac {f(x)}{g(y)}}}{1-{\frac {g(x)}{g(y)}}}}\leq M(x)}
โดยที่เมือ
y
{\displaystyle y}
c
{\displaystyle c}
f
(
x
)
g
(
y
)
{\displaystyle {\frac {f(x)}{g(y)}}}
g
(
x
)
g
(
y
)
{\displaystyle {\frac {g(x)}{g(y)}}}
m
(
x
)
≤
lim inf
y
∈
S
x
f
(
y
)
g
(
y
)
≤
lim sup
y
∈
S
x
f
(
y
)
g
(
y
)
≤
M
(
x
)
.
{\displaystyle m(x)\leq \liminf _{y\in S_{x}}{\frac {f(y)}{g(y)}}\leq \limsup _{y\in S_{x}}{\frac {f(y)}{g(y)}}\leq M(x).}
ลิมิตอินฟิเรียร์ และลิมิตซูพีเรียร์ นั้นจำเป็นเนื่องจากการมีอยู่ของลิมิต
f
g
{\textstyle {\frac {f}{g}}}
แบ่งได้เป็นสองกรณีได้แก่
lim
x
→
c
m
(
x
)
=
lim
x
→
c
M
(
x
)
=
lim
x
→
c
f
′
(
x
)
g
′
(
x
)
=
L
{\displaystyle \lim _{x\to c}m(x)=\lim _{x\to c}M(x)=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}=L}
และ
lim
x
→
c
(
lim inf
y
∈
S
x
f
(
y
)
g
(
y
)
)
=
lim inf
x
→
c
f
(
x
)
g
(
x
)
{\displaystyle \lim _{x\to c}\left(\liminf _{y\in S_{x}}{\frac {f(y)}{g(y)}}\right)=\liminf _{x\to c}{\frac {f(x)}{g(x)}}}
lim
x
→
c
(
lim sup
y
∈
S
x
f
(
y
)
g
(
y
)
)
=
lim sup
x
→
c
f
(
x
)
g
(
x
)
{\displaystyle \lim _{x\to c}\left(\limsup _{y\in S_{x}}{\frac {f(y)}{g(y)}}\right)=\limsup _{x\to c}{\frac {f(x)}{g(x)}}}
ในกรณีแรก ทฤษฎีบทการบีบ บอกได้ว่า
lim
x
→
c
f
(
x
)
g
(
x
)
{\displaystyle \lim _{x\to c}{\frac {f(x)}{g(x)}}}
L
{\displaystyle L}
ทฤษฎีบทการบีบ ยังบอกได้ว่า
lim inf
x
→
c
f
(
x
)
g
(
x
)
=
lim sup
x
→
c
f
(
x
)
g
(
x
)
=
L
{\displaystyle \liminf _{x\to c}{\frac {f(x)}{g(x)}}=\limsup _{x\to c}{\frac {f(x)}{g(x)}}=L}
lim
x
→
c
f
(
x
)
g
(
x
)
{\displaystyle \lim _{x\to c}{\frac {f(x)}{g(x)}}}
L
{\displaystyle L}
ในกรณีที่สอง สมมติฐานที่ว่า
f
(
x
)
{\displaystyle f(x)}
|
g
(
x
)
|
{\displaystyle |g(x)|}
x
{\displaystyle x}
c
{\displaystyle c}
f
{\displaystyle f}
g
{\displaystyle g}
f
(
x
)
{\displaystyle f(x)}
f
(
x
)
{\displaystyle f(x)}
[ 5]
↑ O'Connor, John J.; Robertson, Edmund F. "De L'Hopital biography" . The MacTutor History of Mathematics archive . Scotland: School of Mathematics and Statistics, University of St Andrews. สืบค้นเมื่อ 21 December 2008 . {{cite web }}: CS1 maint: url-status (ลิงก์ )↑ Boyer, Carl B.; Merzbach, Uta C. (2011-01-25). A History of Mathematics ISBN 978-0-470-63056-3 ↑ (Chatterjee 2005 , p. 291)
↑ (Krantz 2004 , p.79)
↑ "L'Hopital's Theorem" . IMOmath . International Mathematical Olympiad . คลังข้อมูลเก่าเก็บจากแหล่งเดิม เมื่อ 2021-05-06. สืบค้นเมื่อ 2024-03-11 .
Chatterjee, Dipak (2005), Real Analysis , PHI Learning Pvt. Ltd, ISBN 81-203-2678-4 Krantz, Steven G. (2004), A handbook of real variables. With applications to differential equations and Fourier analysis , Boston, MA: Birkhäuser Boston Inc., pp. xiv+201, doi :10.1007/978-0-8176-8128-9 , ISBN 0-8176-4329-X MR 2015447 Taylor, A. E. (1952), "L'Hospital's rule", Amer. Math. Monthly , 59 (1): 20–24, doi :10.2307/2307183 , ISSN 0002-9890 , JSTOR 2307183 , MR 0044602 Wazewski, T. (1949), "Quelques démonstrations uniformes pour tous les cas du théorème de l'Hôpital. Généralisations", Prace Mat.-Fiz. (ภาษาฝรั่งเศส), 47 : 117–128, MR 0034430 Lettenmeyer, F. (1936), "Über die sogenannte Hospitalsche Regel", Journal für die reine und angewandte Mathematik , 1936 (174): 246–247, doi :10.1515/crll.1936.174.246 , S2CID 199546754





























![{\displaystyle {\begin{aligned}\lim _{x\to 0}{\frac {e^{x}-1}{x^{2}+x}}&=\lim _{x\to 0}{\frac {{\frac {d}{dx}}(e^{x}-1)}{{\frac {d}{dx}}(x^{2}+x)}}\\[4pt]&=\lim _{x\to 0}{\frac {e^{x}}{2x+1}}\\[4pt]&=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61dc9bd7af6ec9ab9e48ff29b32da5114f95a666)

![{\displaystyle {\begin{aligned}\lim _{x\to 0}{\frac {2\sin(x)-\sin(2x)}{x-\sin(x)}}&=\lim _{x\to 0}{\frac {2\cos(x)-2\cos(2x)}{1-\cos(x)}}\\[4pt]&=\lim _{x\to 0}{\frac {-2\sin(x)+4\sin(2x)}{\sin(x)}}\\[4pt]&=\lim _{x\to 0}{\frac {-2\cos(x)+8\cos(2x)}{\cos(x)}}\\[4pt]&={\frac {-2+8}{1}}\\[4pt]&=6\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1a3d962ee862222679e01afff611a616cd38e64)






![{\displaystyle {\begin{aligned}\lim _{h\to 0}{\frac {f(x+h)+f(x-h)-2f(x)}{h^{2}}}&=\lim _{h\to 0}{\frac {f'(x+h)-f'(x-h)}{2h}}\\[4pt]&=\lim _{h\to 0}{\frac {f''(x+h)+f''(x-h)}{2}}\\[4pt]&=f''(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/244526aca354ac72456ea81b77682fd54a544ede)










![{\displaystyle {\begin{aligned}\lim _{x\to 1}\left({\frac {x}{x-1}}-{\frac {1}{\ln x}}\right)&=\lim _{x\to 1}{\frac {x\cdot \ln x-x+1}{(x-1)\cdot \ln x}}&\quad (1)\\[6pt]&=\lim _{x\to 1}{\frac {\ln x}{{\frac {x-1}{x}}+\ln x}}&\quad (2)\\[6pt]&=\lim _{x\to 1}{\frac {x\cdot \ln x}{x-1+x\cdot \ln x}}&\quad (3)\\[6pt]&=\lim _{x\to 1}{\frac {1+\ln x}{1+1+\ln x}}&\quad (4)\\[6pt]&=\lim _{x\to 1}{\frac {1+\ln x}{2+\ln x}}\\[6pt]&={\frac {1}{2}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d20b9715e349d99ea36894fe15b36cb47a400eda)


















![{\displaystyle {\begin{aligned}&\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f(x)-0}{g(x)-0}}=\lim _{x\to c}{\frac {f(x)-f(c)}{g(x)-g(c)}}\\[6pt]={}&\lim _{x\to c}{\frac {\left({\frac {f(x)-f(c)}{x-c}}\right)}{\left({\frac {g(x)-g(c)}{x-c}}\right)}}={\frac {\lim \limits _{x\to c}\left({\frac {f(x)-f(c)}{x-c}}\right)}{\lim \limits _{x\to c}\left({\frac {g(x)-g(c)}{x-c}}\right)}}={\frac {f'(c)}{g'(c)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78611fcf2c588d4360239c51a0d8a6f3402051d1)


































