การหาปริพันธ์ทีละส่วน

ในแคลคูลัส และในคณิตวิเคราะห์ การหาปริพันธ์ทีละส่วน (อังกฤษ: Integration by parts หรือ Partial Integration) เป็นทฤษฎีบทที่เชื่อมโยงระหว่างปริพันธ์ของผลคูณฟังก์ชันคู่หนึ่ง กับปริพันธ์ของอนุพันธ์และปฏิยานุพันธ์ของฟังก์ชันคู่นั้น มีการหาปริพันธ์วิธีนี้อย่างบ่อยครั้ง โดยการแปลงรูปฟังก์ชันที่หาปฏิยานุพันธ์ยาก แล้วหาปฏิยานุพันธ์ของฟังก์ชันที่หาได้ง่ายกว่า กฎนี้สามารถแปลงให้อยู่ในรูปอย่างง่ายในหนึ่งบรรทัดโดยการหาปริพันธ์ของกฎผลคูณอนุพันธ์

กำหนดให้ u = u(x) และ du = u′(x) dx และกำหนดให้ v = v(x) และ dv = v′(x) dx สำหรับการหาปริพันธ์ทีละส่วน จะได้ว่า

$\int u(x)v'(x)\,dx=u(x)v(x)-\int v(x)\,u'(x)dx$

หรือในรูปที่กระทัดรัดกว่า

$\int u\,dv=uv-\int v\,du\!$

ทฤษฎีบท

ผลคูณของสองฟังก์ชัน

ทฤษฎีบทนี้แสดงได้ดังสมการข้างล่างนี้ สมมติว่า u(x) และ v(x) เป็นฟังก์ชันที่หาอนุพันธ์ได้ จากกฎผลคูณ (ในสัญกรณ์ของไลบ์นิซ):

${\frac {d}{dx}}{\Big (}u(x)v(x){\Big )}=v(x){\frac {d}{dx}}\left(u(x)\right)+u(x){\frac {d}{dx}}\left(v(x)\right)\!$

หาปริพันธ์ทั้งสองข้างเทียบกับ x

$\int {\frac {d}{dx}}\left(u(x)v(x)\right)\,dx=\int u'(x)v(x)\,dx+\int u(x)v'(x)\,dx$

จากนั้นใช้นิยามของปริพันธ์ไม่จำกัดเขต

$u(x)v(x)=\int u'(x)v(x)\,dx+\int u(x)v'(x)\,dx$

$\int u(x)v'(x)\,dx=u(x)v(x)-\int u'(x)v(x)\,dx$

จะได้สูตรสำหรับการหาปริพันธ์ทีละส่วน

เมื่อ du และ dv เป็นผลต่างอนุพัทธ์ของฟังก์ชันของตัวแปร x

$du=u'(x)dx\quad dv=v'(x)dx$

$\int u(x)\,dv=u(x)v(x)-\int v(x)\,du$

ปริพันธ์ทางซ้ายของสมการ ∫uv′ dx ประกอบด้วย v′ (อนุพันธ์ของ v) เพื่อที่จะใช้ทฤษฎีบทนี้ได้นั้น ต้องหาค่า v (ปฏิยานุพันธ์ของ v′) ก่อน แล้วจึงหาปริพันธ์ทางขวา ∫vu′ dx

การตีความโดยใช้กราฟ

การตีความทฤษฎีบทนี้โดยใช้กราฟ เส้นโค้งในภาพขึ้นอยู่กับตัวแปร t

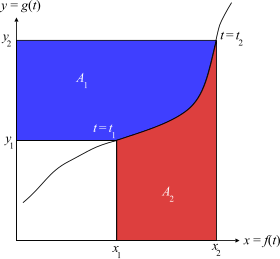
กำหนดเส้นโค้งพาราเมตริก (x, y) = (f(t), g(t)) สมมติว่าเส้นโค้งนี้เป็นฟังก์ชันหนึ่งต่อหนึ่ง เราจะสามารถกำหนดได้ว่า

$x(y)=f(g^{-1}(y))$

$y(x)=g(f^{-1}(x))$

พื้นที่ของบริเวณสีน้ำเงินคือ

$A_{1}=\int _{y_{1}}^{y_{2}}x(y)dy$

ในทำนองเดียวกัน พื้นที่ของบริเวณสีแดง คือ

$A_{2}=\int _{x_{1}}^{x_{2}}y(x)dx$

พื้นที่รวม A₁ + A₂ มีค่าเท่ากับพื้นที่ของรูปสี่เหลี่ยมใหญ่ x₂y₂ ลบด้วยพื้นที่ของรูปเล็ก x₁y₁:

$\overbrace {\int _{y_{1}}^{y_{2}}x(y)dy} ^{A_{1}}+\overbrace {\int _{x_{1}}^{x_{2}}y(x)dx} ^{A_{2}}={\biggl .}x.y(x){\biggl |}_{x1}^{x2}={\biggl .}y.x(y){\biggl |}_{y1}^{y2}$

สมมติว่าเส้นโค้งนี้เรียบในบริเวณใกล้เคียง ทำให้กล่าวถึงปริพันธ์ไม่จำกัดเขต:

$\int xdy+\int ydx=xy$

จัดรูปใหม่:

$\int xdy=xy-\int ydx$

เพราะฉะนั้น การหาปริพันธ์ทีละส่วนสามารถพิจารณาได้ว่าพื้นที่สีน้ำเงินมาจากพื้นที่รวมลบด้วยพื้นที่สีแดง

การตีความให้เห็นภาพนี้ยังอธิบายได้ว่าทำไมการหาปริพันธ์ทีละส่วนสามารถหาปริพันธ์ของฟังก์ชันผกผัน f⁻¹(x) ได้ เมื่อทราบปริพันธ์ของฟังก์ชัน f(xv) อันที่จริงแล้ว ฟังก์ชัน x(y) และ y(x) เป็นส่วนกลับกัน และปริพันธ์ ∫x dy สามารถคำนวณได้ดังข้างบน เมื่อทราบปริพันธ์ ∫y dx

อ้างอิง

• Evans, Lawrence C. (1998). Partial Differential Equations. Providence, Rhode Island: American Mathematical Society. ISBN 0-8218-0772-2.
• Arbogast, Todd; Bona, Jerry (2005). Methods of Applied Mathematics (PDF).
• Horowitz, David (September 1990). "Tabular Integration by Parts". The College Mathematics Journal. 21 (4): 307–311. doi:10.2307/2686368. JSTOR 2686368.

แหล่งข้อมูลอื่น

• Hazewinkel, Michiel, บ.ก. (2001), "Integration by parts", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
• Integration by parts—from MathWorld