เรขาคณิตเชิงพีชคณิต

| เรขาคณิต |
|---|
 |
| นักเรขาคณิต |
เรขาคณิตเชิงพีชคณิต (อังกฤษ: Algebraic geometry) เป็นสาขาหนึ่งของคณิตศาสตร์ที่เริ่มแรกศึกษารากของพหุนามหลายตัวแปร โดยอาศัยวิธีการทางพีชคณิตนามธรรม โดยเฉพาะอย่างยิ่งเครื่องมือจากพีชคณิตสลับที่เพื่อใช้การแก้ปัญหาทางเรขาคณิตเกี่ยวกับเซตของรากของพหุนามดังกล่าว
วัตถุพื้นฐานของการศึกษาในเรขาคณิตเชิงพีชคณิตคือวาไรตีเชิงพีชคณิต (Algebraic variety) ซึ่งเป็นผลเฉลยของระบบสมการพหุนามเมื่อมองว่าเป็นวัตถุเรขาคณิต ตัวอย่างวาไรตีเชิงพีชคณิตที่ได้รับการศึกษามากที่สุด เช่น เส้นโค้งเชิงพีชคณิตระนาบ ซึ่งรวมถึง เส้นตรง วงกลม พาราโบลา วงรี ไฮเพอร์โบลา, เส้นโค้งคิวบิก เช่น เส้นโค้งเชิงวงรี และเส้นโค้งควอร์ติกเช่น เลมนิสเคต และ วงรีแคสสินี เส้นโค้งข้างต้นมีจุดบนเส้นโค้งบางจุดที่มีความสำคัญและมีทฤษฎีที่เกี่ยวข้อง อาทิเช่น จุดเอกฐาน จุดเปลี่ยนเว้า และจุดที่ตำแหน่งอนันต์ ส่วนทฤษฎีขั้นสูงของเรขาคณิตเชิงพีชคณิตสนใจทอพอโลยีของเส้นโค้งต่าง ๆ และความสัมพันธ์ระหว่างเส้นโค้งแต่ละเส้น
เรขาคณิตเชิงพีชคณิตเป็นหัวใจสำคัญของคณิตศาสตร์สมัยใหม่ และมีความเชื่อมโยงไปยังสาขาต่าง ๆ จำนวนมาก เช่น การวิเคราะห์เชิงซ้อน ทอพอโลยี และ ทฤษฎีจำนวน ตลอดจนมีบทประยุกต์ในการออกแบบการทดลองในสถิติเชิงคณิตศาสตร์[1]
แนวคิดพื้นฐาน
[แก้]รากของระบบพหุนาม
[แก้]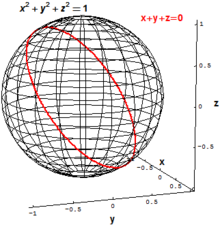
ในเรขาคณิตเชิงพีชคณิต นักคณิตศาสตร์ศึกษารากของระบบสมการพหุนาม ซึ่งสามารถมองได้ว่าเป็นเซตของจุดในปริภูมิมิติต่าง ๆ ตัวอย่างเช่น ทรงกลมที่มีรัศมีเท่ากับ 1 ในปริภูมิแบบยุคลิดสามมิติ R3 เป็นเซตของจุด (x,y,z) ∈ R3 ทั้งหมดที่ทำให้
อีกตัวอย่างหนึ่ง วงกลมเอียง ใน R3 ซึ่งเกิดจากเซตของจุด (x,y,z) ทั้งหมดที่สอดคล้องกับระบบสมการพหุนามสองสมการ
วาไรตีเชิงพีชคณิต
[แก้]วาไรตีเชิงพีชคณิต (Algebraic variety) เป็นวัตถุพื้นฐานที่ศึกษาในเรขาคณิตเชิงพีชคณิต ในที่นี้เราสนใจวาไรตีในเรขาคณิตเชิงพีชคณิตคลาสสิค ซึ่งมีนิยามดังนี้
วาไรตี V เหนือ Rn (หรือ Cn) เป็นเซตของจุด (x1,...,xn) ที่สอดคล้องกับระบบสมการพหนุม fi (x1,...,xn) สำหรับแต่ละ i = 1, 2, ...
เส้นโค้งเชิงพีชคณิตคือวาไรตีเชิงพีชคณิตที่มี n = 2 วาไรตีเชิงพีชคณิตที่พื้นฐานที่สุด ได้แก่ วาไรตีสัมพรรค (Affine variety) และวาไรตีเชิงภาพฉาย หรือวาไรตีโพรเจคทีฟ (Projective variety)
ฟังก์ชันพหุนามและเซตเชิงพีชคณิต
[แก้]ให้ เป็นฟิลด์ ในเรขาคณิตเชิงพีชคณิตคลาสสิกนิยมใช้ฟิลด์จำนวนเชิงซ้อน C แต่เราสามารถเปลี่ยน C เป็นฟีลด์ที่มีสมบัติปิดเชิงพีชคณิตใด ๆ ได้ (นั่นคือทุกพหุนามดีกรีมากกว่า 1 ในฟิลด์ มีรากเสมอ) โดยที่ทฤษฎีทั่วไปยังคงเป็นจริง
เราสนใจปริภูมิสัมพรรค (Affine space) มิติ n เหนือฟิลด์ k ซึ่งเขียนแทนด้วย (บางครั้งเขียน เมื่อ ชัดเจนจากบริบท) สังเกตว่า หากเรากำหนดระบบพิกัดฉากให้ แล้ว จะกลายเป็นปริภูมิเวกเตอร์ เหตุผลที่เราไม่พิจารณา โดยตรงก็เพื่อ "ลืม" ว่า มีโครงสร้างเป็นปริภูมิเวกเตอร์
ฟังก์ชัน จะเป็น ฟังก์ชันพหุนาม (หรือ ฟังก์ชันปกติ) หากสามารถเขียนเป็นพหุนามได้ นั่นคือถ้ามีพหุนาม ที่ทำให้ สำหรับทุกจุด ที่มีพิกัด ใน ในกรณีที่ฟีลด์ของเราเป็นฟิลด์ปิดเชิงพีชคณิต (หรือโดยทั่วไปกว่าเมื่อฟิลด์เป็นฟิลด์อนันต์) จะมีความสัมพันธ์ 1-1 ทั่วถึงระหว่างฟังก์ชันพหุนามและพหุนามใน ซึ่งทำให้เซตของฟังก์ชันพหุนามทั้งหมดเป็นริง เรียกว่า ริงของฟังก์ชันพหุนาม และเขียนแทนด้วย [2]
ให้ เป็นเซตของพหุนามใน เซตศูนย์ หรือ เซตแวนิชชิง (Zero set หรือ Vanishing set) ของ S คือเซต ของจุดทั้งหมดใน ที่ทำให้พหุนามทุกตัวใน เป็นศูนย์ที่จุดนั้น ตามนิยามด้านล่าง
จะเรียกสับเซต ใด ๆ ของ ว่าเป็น เซตเชิงพีชคณิต (Algebraic set) ถ้าหาก สามารถเขียนได้ในรูป สำหรับบางเซต
ความสมมูลระหว่างเรขาคณิต-พีชคณิต
[แก้]เราสนใจปัญหาที่ว่า หากระบุสับเซต ใด ๆ ของ มา สามารถหาเซตของพหุนาม ที่ก่อกำเนิด (หรือก็คือ ) ได้หรือไม่
นิยามเซต แทนเซตของพหุนามทั้งหมดที่เซตศูนย์ของมันมี เป็นสับเซต สัญลักษณ์ มาจากสมบัติที่ว่าเซตดังกล่าวเป็นไอดีลของ
จากนิยามข้างต้น ทำให้เกิดคำถามต่อไปนี้
- กำหนดเซต ใด ๆ เมื่อไรที่
- กำหนดเซตของพหุนาม เมื่อไรที่
คำตอบของคำถามแรกได้จากการกำหนดทอพอโลยีบน เรียกว่า ทอพอโลยีซาริสกี (Zariski topology) ซึ่งเซตปิดบนทอพอโลยีดังกล่าว ได้แก่เซตเชิงพีชคณิตทั้งหมด และทอพอโลยีนี้สะท้อนโครงสร้างพีชคณิตของ แล้วจะได้ว่า ก็ต่อเมื่อ เป็นเซตเชิงพีชคณิต หรือเซตปิดในทอพอโลยีซาริสกี ส่วนคำถามที่สองนั้นเป็นผลจากทฤษฎีบทที่เรียกว่า ฮิลแบร์ทนูลสเต็ลเลินซาต์ส หรือ ทฤษฎีบทโลคัส-ศูนย์ของฮิลแบร์ท (Hilbert's Nullstellensatz) ซึ่งกล่าวว่า เป็นราดิคัลของไอดีลที่ก่อกำเนิดโดย ผลลัพธ์จากทฤษฎีทั้งสองระบุว่า ไอดีลใน และเซตเชิงพีชคณิตใน เป็นอย่างเดียวกัน
วาไรตีสัมพรรค
[แก้]เซตเชิงพีชคณิตจะเป็น เซตลดรูปไม่ได้ (Irreducible set) หากมันไม่เป็นยูเนียนของเซตเชิงพีชคณิตที่เล็กกว่าสองเซตได้ เราพบว่า เซตเชิงพีชคณิตใด ๆ อยู่ในรูปยูเนียนจำกัดของเซตเชิงพีชคณิตที่ลดรูปไม่ได้ และการแยกส่วนแบบดังกล่าวมีได้แบบเดียว ดังนั้นส่วนประกอบหรือเซตเชิงพีชคณิตที่ลดรูปไม่ได้ดังกล่าวจึงถูกเรียกว่า ส่วนประกอบที่ไม่สามารถลดรูปได้ (Irreducible components) ของเซตพีชคณิต เซตเชิงพีชคณิตที่ลดรูปไม่ได้เรียกอีกอย่างว่า วาไรตี หรือ วาไรตีสัมพรรค เพื่อระบุเจาะจงว่าเราทำงานอยู่ในปริภูมิสัมพรรค
มีทฤษฎีบทว่า เซตเชิงพีชคณิตจะเป็นวาไรตีก็ต่อเมื่อ มีไอดีลเฉพาะ ของ ที่ทำให้เซตเชิงพีชคณิตนั้นเป็นเซตศูนย์ของไอดีล
ประวัติ
[แก้]ส่วนนี้รอเพิ่มเติมข้อมูล คุณสามารถช่วยเพิ่มข้อมูลส่วนนี้ได้ |
คริสต์ศตวรรษที่ 20
[แก้]วาน เดอร์ วาร์เดน, ออสการ์ ซาริสกี และ อองเดร์ แวย์ พัฒนารากฐานสำหรับเรขาคณิตเชิงพีชคณิตโดยอาศัยพีชคณิตสลับที่ รวมถึง ทฤษฎีแวลิวเอชัน (Valuation theory) และทฤษฎีของไอดีล เป้าหมายประการหนึ่งเพื่อสร้างกรอบโครงร่างที่รัดกุมเพื่อใช้พิสูจน์ผลงานของนักคณิตศาสตร์ด้านเรขาคณิตเชิงพีชคณิตสกุลอิตาลี ทั้งนี้เพราะว่า นักคณิตศาสตร์ในสกุลนี้ใช้แนวคิดเรื่อง จุดทั่วไป (Generic points) ในงานคณิตศาสตร์โดยไม่มีคำจำกัดความที่ชัดเจน นิยามจุดทั่วไปกำหนดเป็นครั้งแรกโดยนักคณิตศาสตร์ข้างต้นในช่วงทศวรรษ 1930
ในช่วงทศวรรษที่ 1950 และ 1960 ฌ็อง-ปิแยร์ แซร์ และ อเล็กซองดร์ โกรเธนดีก สร้างรากฐานใหม่โดยใช้ ทฤษฎีชีฟ (Sheaf theory) ในภายหลังโกรเธนดีกได้ริเริ่มเสนอแนวคิดเกี่ยวกับ สกีม (Scheme) ร่วมกับวิธีการทางฮอมอโลยี
วาไรตีที่สำคัญรูปแบบหนึ่งคือ วาไรตีอาบีเลียน ซึ่งเป็นวาไรตีเชิงภาพฉายที่มีจุดบนวาไรตีนี้เป็นกรุปอาบีเลียน ตัวอย่างต้นแบบของวาไรตีอาบีเลียนคือ เส้นโค้งเชิงวงรี ซึ่งมีทฤษฎีที่เกี่ยวข้องมากมาย เส้นโค้งเชิงวงรีเป็นเครื่องมือในการพิสูจน์ทฤษฎีบทสุดท้ายของแฟร์มาต์ และยังใช้ใน การเข้ารหัสเส้นโค้งเชิงวงรีอีกด้วย
อ้างอิง
[แก้]- ↑ Drton, Mathias (2009). Lectures on algebraic statistics. Bernd Sturmfels, Seth Sullivant. Basel: Birkhäuser. ISBN 978-3-7643-8905-5. OCLC 405547762.
- ↑ Cutkosky, Steven Dale (2018). Introduction to algebraic geometry. Providence, Rhode Island. ISBN 978-1-4704-4670-3. OCLC 1039613757.
ดูเพิ่ม
[แก้]- Hartshorne, Robin (1977). Algebraic geometry. New York: Springer. ISBN 0-387-90244-9. OCLC 2798099.
- Cutkosky, Steven Dale (2018). Introduction to Algebraic Geometry. Providence, Rhode Island: American Mathematical Society. ISBN 9781470435189.
- Reid, Miles (1988). Undergraduate Algebraic Geometry (PDF). Cambridge University Press: Cambridge University Press. ISBN 9781139163699.
- The Rising Sea: Foundations of Algebraic Geometry โดย Ravi Vakil
- The Stacks Project หนังสือโอเพินซอร์สสำหรับอ้างอิงเกี่ยวกับเรขาคณิตเชิงพีชคณิต








![{\displaystyle p\in k[x_{1},\dotsc ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48cb0df4d9ae39e52d1f4780e2f17f4a5a19db04)



![{\displaystyle k[x_{1},\dotsc ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b80378540514094e936c0c11d0f40aba0d3056b)
![{\displaystyle k[\mathbf {A} ^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b78e62afd3865937142f43d535b1bef37150a03)




![{\displaystyle S\subseteq k[\mathbf {A} ^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/915c37992ff17f85b2a9704d1df90ffc80c068cc)






