 วงรีซึ่งมาจากการตัดของทรงกรวยกับระนาบ
วงรีซึ่งมาจากการตัดของทรงกรวยกับระนาบ
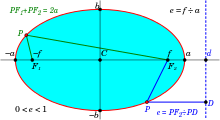 นิยามสองแบบของวงรีซึ่งเทียบเท่ากัน: ใช้โฟกัสสองจุด(เขียว) และใช้โฟกัสกับไดเรกทริกซ์(น้ำเงิน)
นิยามสองแบบของวงรีซึ่งเทียบเท่ากัน: ใช้โฟกัสสองจุด(เขียว) และใช้โฟกัสกับไดเรกทริกซ์(น้ำเงิน)
วงรี (อังกฤษ: ellipse) เป็นเส้นโค้งทางคณิตศาสตร์ซึ่งล้อมรอบจุดโฟกัสสองจุดและทำให้ผลรวมของระยะทางจากจุดบนเส้นโค้งไปหาจุดโฟกัสแต่ละจุดเป็นค่าคงที่ จากนิยามนี้ วงรีถือเป็นนัยทั่วไปของวงกลม นั่นคือ วงกลมเป็นกรณีพิเศษของวงรีที่มีจุดโฟกัสซ้อนกันเป็นจุดเดียว ความยืดของวงรีแสดงด้วยค่าความเยื้องศูนย์กลาง ซึ่งสำหรับวงรีอาจมีค่าได้ตั้งแต่ 0 (กรณีพิเศษของวงกลม) และมากเข้าใกล้ 1 เท่าใดก็ได้ แต่ไม่ถึง 1 (ซึ่งจะกลายเป็นพาราโบลา) วงรียังสามารถนิยามเป็นเซตของจุด ที่สำหรับแต่ละจุดในเซต อัตราส่วนของระยะทางไปหาจุดที่กำหนด(ซึ่งจะเป็นหนึ่งในจุดโฟกัส)ต่อระยะทางไปหาเส้นที่กำหนด(เรียกว่าเส้นไดเรกทริกซ์) เป็นค่าคงที่ ซึ่งค่าคงที่นี้จะเท่ากับความเยื้องศูนย์กลางข้างต้น
วงรีเป็นภาคตัดกรวย นั่นคือ เกิดจากการตัดกันของทรงกรวยกับระนาบ (ดูภาพขวา) และยังเป็นภาคตัดของทรงกระบอก ยกเว้นเฉพาะกรณีที่ระนาบตัดขนานกับแกนทรงกระบอก
วงรีมักนิยามเป็นโลกัสของจุดในระนาบสองมิติ โดยจากจุดโฟกัส  กับ
กับ  และระยะทาง
และระยะทาง  จะนิยามวงรีเป็นเซตของจุด
จะนิยามวงรีเป็นเซตของจุด  ทั้งหมดที่ทำให้ผลบวกของระยะทาง
ทั้งหมดที่ทำให้ผลบวกของระยะทาง  กับ
กับ  เป็น
เป็น  หรือเขียนเป็นสัญกรณ์ว่า
หรือเขียนเป็นสัญกรณ์ว่า  (กรณีที่
(กรณีที่  จะลดรูปเป็นเส้นตรง ดังนั้นเพื่อให้เป็นวงรีจะต้องบังคับ
จะลดรูปเป็นเส้นตรง ดังนั้นเพื่อให้เป็นวงรีจะต้องบังคับ  )
)
จุดกึ่งกลางของส่วนของเส้นตรงเชื่อมจุดโฟกัสทั้งสอง เรียกว่าจุดศูนย์กลางของวงรี เส้นตรงที่ผ่านจุดโฟกัสทั้งสองเรียกว่าแกนเอก และเส้นที่ผ่านจุดศูนย์กลางและตั้งฉากกับแกนเอกเรียกว่าแกนโท แกนเอกตัดกับวงกลมที่จุดยอด ซึ่งห่างจากจุดศูนย์กลาง  หน่วย ระยะทางจากจุดโฟกัสไปจุดศูนย์กลางเรียกว่าระยะโฟกัส
หน่วย ระยะทางจากจุดโฟกัสไปจุดศูนย์กลางเรียกว่าระยะโฟกัส  อัตราส่วน
อัตราส่วน  คือความเยื้องศูนย์กลาง
คือความเยื้องศูนย์กลาง
ในระบบพิกัดคาร์ทีเซียน วงรีที่มีจุดศูนย์กลางที่  แกนเอกขนานแกน x ยาว
แกนเอกขนานแกน x ยาว  แกนโทขนานแกน y ยาว
แกนโทขนานแกน y ยาว  เขียนสมการได้เป็น:
เขียนสมการได้เป็น:

ความเยื้องศูนย์กลางของวงรีเป็นไปตามสูตร

หากใช้ระบบสมการอิงตัวแปรเสริม จะสามารถเขียนวงรีในรูปของฟังก์ชันตรีโกณมิติเป็น

หากแทน  จะได้สมการตัวแปรเสริมอีกรูปคือ
จะได้สมการตัวแปรเสริมอีกรูปคือ

ในพิกัดเชิงขั้ว หากใช้จุดศูนย์กลางของวงรีเป็นจุดกำเนิด และวัดมุมเทียบกับแกนเอก จะได้เป็นสมการ

แต่หากใช่จุดโฟกัสเป็นจุดกำเนิด จะได้สมการที่ง่ายกว่า คือ

วงรีมีพื้นที่  เห็นได้จากการมองวงรีเป็นวงกลมรัศมี
เห็นได้จากการมองวงรีเป็นวงกลมรัศมี  ที่ถูกยืดออก
ที่ถูกยืดออก  เท่า จึงได้พื้นที่เป็น
เท่า จึงได้พื้นที่เป็น  หรืออาจพิสูจน์จากการอินทิเกรต โดยจัดรูปสมการวงรี
หรืออาจพิสูจน์จากการอินทิเกรต โดยจัดรูปสมการวงรี  เป็น
เป็น  อินทิเกรตจาก
อินทิเกรตจาก  ถึง
ถึง  จะได้พื้นที่ครึ่งบน ดังนั้นได้เป็น
จะได้พื้นที่ครึ่งบน ดังนั้นได้เป็น

ความยาวรอบรูปของวงรีไม่สามารถเขียนเป็นสูตรอย่างง่ายได้ โดยมีค่าเท่ากับอินทิกรัล

เมื่อ  เป็นปริพันธ์วงรีสมบูรณ์ชนิดที่สอง (Complete elliptic integral of the second kind)
เป็นปริพันธ์วงรีสมบูรณ์ชนิดที่สอง (Complete elliptic integral of the second kind)

สูตรความยาวรอบรูปสามารถเขียนในรูปอนุกรมอนันต์ได้เป็น
![{\displaystyle {\begin{aligned}C&=2\pi a\left[{1-\left({\frac {1}{2}}\right)^{2}e^{2}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {e^{4}}{3}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}{\frac {e^{6}}{5}}-\cdots }\right]\\&=2\pi a\left[1-\sum _{n=1}^{\infty }\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {e^{2n}}{2n-1}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c454c111fb8b731882a2e7e441cf3881cee99396)
รามานุจันได้ให้สูตรประมาณค่าความยาวรอบรูปว่า
![{\displaystyle C\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\right]=\pi \left[3(a+b)-{\sqrt {10ab+3(a^{2}+b^{2})}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38b3f790cb11678c0ed8bcba9d0ba2660ca42339)



































![{\displaystyle {\begin{aligned}C&=2\pi a\left[{1-\left({\frac {1}{2}}\right)^{2}e^{2}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {e^{4}}{3}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}{\frac {e^{6}}{5}}-\cdots }\right]\\&=2\pi a\left[1-\sum _{n=1}^{\infty }\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {e^{2n}}{2n-1}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c454c111fb8b731882a2e7e441cf3881cee99396)
![{\displaystyle C\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\right]=\pi \left[3(a+b)-{\sqrt {10ab+3(a^{2}+b^{2})}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38b3f790cb11678c0ed8bcba9d0ba2660ca42339)