การเข้ารหัสทางประสาท

การเข้ารหัสทางประสาท (อังกฤษ: Neural coding) เป็นการศึกษาทางประสาทวิทยาศาสตร์ เพื่อกำหนดความสัมพันธ์ระหว่างสิ่งเร้ากับการตอบสนองของเซลล์ประสาทเดี่ยว ๆ หรือของกลุ่มเซลล์ประสาท และความสัมพันธ์ระหว่างการทำงานทางไฟฟ้าของเซลล์ประสาทในกลุ่ม[1][2] โดยอาศัยทฤษฎีว่า การทำงานของเครือข่ายเซลล์ประสาทในสมองจะเป็นตัวแทนข้อมูลทางประสาทสัมผัสและข้อมูลอื่น ๆ นักวิชาการจึงเชื่อว่า เซลล์ประสาทสามารถเข้ารหัสข้อมูลเป็นทั้งแบบดิจิตัลและแบบแอนะล็อก[3]
มุมมองกว้าง ๆ[แก้]
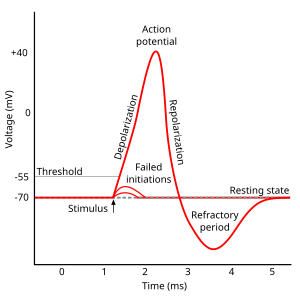
เซลล์ประสาทค่อนข้างจะน่าทึ่งในบรรดาเซลล์ต่าง ๆ ในร่างกาย เพราะสามารถส่งสัญญาณไปอย่างรวดเร็วได้ระยะไกล ๆ ซึ่งดำเนินการโดยอาศัยอิมพัลส์ไฟฟ้าที่เรียกว่า ศักยะงาน ซึ่งส่งไปตามใยประสาท เซลล์ประสาทรับความรู้สึกจะส่งขบวนศักยะงานเป็นจังหวะตามกาลเวลาที่ต่าง ๆ กัน เพื่อตอบสนองต่อสิ่งเร้าภายนอกเช่น แสง เสียง รส กลิ่น และสัมผัส ข้อมูลเกี่ยวกับสิ่งเร้าจะเข้ารหัสเป็นขบวนศักยะงานเช่นนี้ แล้วส่งไปยังทั้งสมองและรอบ ๆ สมอง
แม้ศักยะงานอาจจะต่างกันบ้างเช่นระยะห่างของแต่ละอิมพัลส์ แอมพลิจูด และรูปร่าง แต่งานศึกษารหัสทางประสาทจะปฏิบัติต่อพวกมันเหมือนกับเป็นเหตุการณ์ที่มีรูปแบบตายตัวและเหมือนกัน ถ้าไม่สนใจระยะการดำรงอยู่ของศักยะงาน (ประมาณ 1 มิลลิวินาที) ขบวนหรือลำดับศักยะงาน จะมีลักษณะเป็นลำดับข้อมูลแบบมีหรือไม่มี (all-or-none) คล้าย ๆ สัญญาณดิจิทัล[4] ช่องว่างระหว่างอิมพัลส์ศักยะงานบ่อยครั้งจะต่างกัน โดยดูเหมือนจะเป็นไปโดยสุ่ม[5] การศึกษารหัสทางประสาทจะอาศัยการวัดและกำหนดว่า ลักษณะต่าง ๆ ของสิ่งเร้า เช่นความสว่างของแสง ความดังของเสียง การทำงานของกล้ามเนื้อเช่นทิศทางการเคลื่อนไหวของแขน จะสามารถกำหนดโดยขบวนศักยะงานในเซลล์ประสาทได้อย่างไร เพื่อกำหนดและวิเคราะห์การยิงศักยะงานของเซลล์ประสาท นักวิทยาศาสตร์มักนิยมใช้วิธีการทางสถิติศาสตร์ ทางทฤษฎีความน่าจะเป็น และ stochastic point process
เมื่อมีพัฒนาการของเทคโนโลยีเพื่อบันทึกและถอดรหัสสัญญาณประสาทดีขึ้น ๆ นักวิทยาศาสตรจึงเริ่มเข้าใจสัญญาณทางประสาทได้มากขึ้น ทำให้เริ่มเห็นแสงรำไร ๆ เกี่ยวกับรหัสประสาทตามเวลาจริงเมื่อมีการสร้างและการระลึกถึงความจำในฮิปโปแคมปัส ซึ่งเป็นศูนย์สมองเกี่ยวกับการสร้างความจำ[6][7] และนักประสาทวิทยาศาสตร์ก็ได้ริเริ่มโครงการถอดรหัสสัญญาณสมองขนาดใหญ่หลายโครงการ[8][9]
การเข้าและการถอดรหัส[แก้]
ความสัมพันธ์ระหว่างสิ่งเร้ากับการตอบสนองของระบบประสาทสามารถศึกษาได้จากมุมตรงกันข้าม 2 ด้าน
- การเข้ารหัสทางประสาท (Neural encoding) ก็คือการแปลสิ่งเร้าเป็นการตอบสนองของเซลล์ประสาท ประเด็นการศึกษาหลักก็เพื่อเข้าใจว่า นิวรอนจะตอบสนองอย่างไรต่อสิ่งเร้าต่าง ๆ แล้วสร้างแบบจำลองเพื่อใช้พยากรณ์การตอบสนองต่อสิ่งเร้าอื่น ๆ
- การถอดรหัสทางประสาท (Neural decoding) ก็จะกลับกัน คือเป็นการแปลการตอบสนองทางประสาทเป็นสิ่งเร้า โดยเป้าหมายก็คือการระบุสิ่งเร้า หรือลักษณะบางอย่างของสิ่งเร้านั้น จากขบวนศักยะงานที่เซลล์ประสาทสร้างเพื่อตอบสนอง
สมมติฐานการเข้ารหัสต่าง ๆ[แก้]
ขบวนหรือลำดับศักยะงานอาจมีข้อมูลที่เข้ารหัสโดยแผนการต่าง ๆ กัน เช่น ในเซลล์ประสาทสั่งการ (motor neuron) กล้ามเนื้อที่เชื่อมกับเซลล์ประสาทจะออกแรงโดยขึ้นอยู่กับอัตราการยิงศักยะงานเท่านั้น ซึ่งก็คือจำนวนศักยะงานต่อช่วงเวลาหนึ่ง ๆ โดยเฉลี่ย นี่เป็นการเข้ารหัสโดยอัตรา (rate coding) ในนัยตรงกันข้าม รหัสโดยเวลา (temporal code) ที่ซับซ้อนจะขึ้นอยู่กับการยิงสัญญาณในช่วงเวลาแต่ละระยะ ๆ อย่างแม่นยำ ซึ่งอาจเกิดเพราะจับคู่กับสิ่งเร้าภายนอก ดังที่พบในระบบการเห็น[10] และระบบการได้ยิน หรืออาจเกิดในวงจรประสาทเองโดยธรรมชาติ[11]
ประเด็นว่า นิวรอนจะใช้รหัสโดยอัตรา หรือรหัสโดยเวลา เป็นเรื่องที่ได้ความสนใจอย่างมากภายในชุมชนนักประสาทวิทยาศาสตร์ แม้จะยังไม่มีนิยามที่แน่นอนว่า คำเหล่านี้หมายความว่าอะไร ในทฤษฎีหนึ่งที่เรียกว่า neuroelectrodynamics (พลวัตทางประสาทไฟฟ้า) การเข้ารหัสที่จะกล่าวต่อไปเหล่านี้ล้วนพิจารณาว่าเป็นอนุปรากฏการณ์ (epiphenomena)[A] ซึ่งมีเหตุจากการเปลี่ยนแปลงในระดับโมเลกุลที่สะท้อนการกระจายตามพื้นที่ของสนามไฟฟ้าภายในนิวรอน โดยเป็นผลของสเปกตรัมแม่เหล็กไฟฟ้าที่มีพิสัยกว้างของศักยะงาน และข้อมูลจะปรากฏเป็น spike directivity[12][13][14][15][16]
การเข้ารหัสโดยอัตรา (Rate coding)[แก้]
แบบจำลองการเข้ารหัสโดยอัตราเพื่อสื่อข้อมูลเสนอว่า เมื่อระดับของสิ่งเร้า (เช่นความสว่างของแสง) เพิ่มขึ้น อัตราของศักยะงานที่เซลล์ส่งก็จะเพิ่มขึ้นด้วย การเข้ารหัสโดยอัตรา (Rate coding) บางครั้งก็เรียกว่า การเข้ารหัสโดยความถี่ (frequency coding) ด้วยเหมือนกัน
รหัสนี้เป็นแบบดั้งเดิม โดยสมมุติว่า ข้อมูลเกี่ยวกับสิ่งเร้าเกือบทั้งหมดหรือทั้งหมดจะเข้ารหัสเป็นอัตราของศักยะงาน แต่เพราะลำดับการส่งศักยะงานตอบสนองต่อสิ่งเร้าหนึ่ง ๆ จะเปลี่ยนไปเมื่อทดลองแต่ละครั้ง ๆ การตอบสนองของเซลล์จึงต้องดำเนินการโดยวิธีการทางสถิติหรือตามความน่าจะเป็น และกำหนดข้อมูลเป็นอัตราการยิงสัญญาณ ไม่ใช่ลำดับการยิงสัญญาณโดยเฉพาะ ๆ ในระบบรับความรู้สึกส่วนมาก โดยทั่วไปอัตราการยิงสัญญาณจะเพิ่มขึ้นแบบไม่ใช่เชิงเส้นตามระดับของสิ่งเร้า[17]
แบบจำลองนี้จะไม่ให้ความสำคัญแก่ข้อมูลที่ระบบประสาทอาจเข้ารหัสเป็นระยะเวลาในระหว่างขบวนศักยะงาน ดังนั้น รหัสโดยอัตราจึงมีประสิทธิภาพที่ไม่ดี แต่ก็ทนทานต่อเสียงรบกวนได้ดีมาก[5] (เหมือนสัญญาณดิจิทัล) เมื่อเข้ารหัสโดยอัตรา การคำนวณอัตราศักยะงานอย่างแม่นยำจะเป็นเรื่องสำคัญมาก และจริง ๆ แล้ว คำว่า อัตราการยิงสัญญาณ (firing rate) ก็มีหลายความหมายหลายนิยาม โดยต่างกันตามวิธีหาค่าเฉลี่ย เช่น ค่าเฉลี่ยตามเวลา หรือค่าเฉลี่ยที่ได้จากการทดลองที่ทำซ้ำ ๆ
เมื่อเข้ารหัสโดยกระบวนการนี้ การเรียนรู้จะเกิดผ่านการเปลี่ยนความสำคัญของสัญญาณที่ส่งผ่านไซแนปส์โดยขึ้นอยู่กับการทำงาน (activity-dependent synaptic weight modifications)
นักสรีรวิทยาไฟฟ้าชาวอังกฤษ ดร. เอ็ดการ์ เอเดรียน และนักสรีวิทยาประสาทชาวสวีเด็น Yngve Zotterman ได้แสดงการเข้ารหัสของประสาทโดยอัตราเป็นครั้งแรกในปี พ.ศ. 2469[18] การทดลองดั้งเดิมนี้ได้แขวนน้ำหนักขนาดต่าง ๆ จากกล้ามเนื้อ เมื่อน้ำหนักเพิ่มขึ้น อัตราการส่งศักยะงานจากเส้นประสาทรับความรู้สึกที่อยู่ในกล้ามเนื้อก็เพิ่มขึ้นด้วย จากงานทดลองดั้งเดิมนี้ นักวิทยาศาสตร์ทั้งสองจึงสรุปว่า ศักยะงานเป็นเหตุการณ์เดี่ยว ๆ และความถี่ของการเกิดเหตุการณ์ ไม่ใช่ขนาดของเหตุการณ์แต่ละเหตุการณ์ ๆ เป็นมูลฐานการสื่อสารระหว่างนิวรอน
ในทศวรรษต่อ ๆ มา การวัดอัตราการส่งสัญญาณกลายเป็นมาตรฐานเพื่อระบุคุณสมบัติต่าง ๆ ของเซลล์ประสาทรับความรู้สึกและเซลล์ประสาทในเปลือกสมองส่วนต่าง ๆ โดยส่วนหนึ่งก็เพราะมันวัดได้ง่ายเทียบกับวิธีอื่น ๆ แต่วิธีนี้ก็ไม่สนใจข้อมูลอื่น ๆ ที่อาจจะมาจากระยะการส่งสัญญาณอย่างแม่นยำของนิวรอน งานศึกษาปี 2548 ได้อ้างหลักฐานทางการทดลองต่าง ๆ เพื่อเสนอว่า อัตราการยิงสัญญาณที่เฉลี่ยจำนวนศักยะงานตามกาลเวลาธรรมดา ๆ อาจจะไม่สมบูรณ์พอเพื่ออธิบายการทำงานของสมอง[5]
อัตรานับศักยะงาน (Spike-count rate)[แก้]
spike-count rate (อัตรานับศักยะงาน) หรือเรียกอีกอย่างว่า temporal average (ค่าเฉลี่ยตามเวลา) วัดได้โดยนับจำนวนศักยะงานที่ปรากฏในช่วงการทดลองเดียวแล้วหารด้วยระยะเวลา ผู้ทำการทดลองจะกำหนด T ซึ่งเป็นระยะเวลา โดยขึ้นกับประเภทนิวรอนที่กำลังบันทึกค่า แต่โดยปกติแล้ว เพื่อให้สมเหตุสมผล ก็จะต้องมีศักยะงานมากกว่าหนึ่งพัลส์ที่เกิดภายในช่วง ดังนั้น ค่า T ปกติจะอยู่ที่ 100 มิลลิวินาที หรือ 500 มิลลิวินาที แต่ก็อาจจะสั้นยาวกว่านั้น[19]
อัตรานับศักยะงานจะกำหนดได้ด้วยการทดลองเพียงแค่ครั้งเดียว แต่ก็แลกกับการไม่ได้รายละเอียดทางเวลาของการตอบสนองที่ต่าง ๆ กันตามธรรมชาติในระยะที่ทำการทดลอง รหัสเช่นนี้จึงดีในกรณีที่สิ่งเร้ามีระดับสม่ำเสมอหรือเปลี่ยนอย่างช้า ๆ โดยสัตว์ไม่จำเป็นต้องตอบสนองอย่างรวดเร็ว ซึ่งเป็นสถานการณ์ที่มักใช้ในเกณฑ์วิธีการทดลองอยู่แล้ว แต่สิ่งเร้าในโลกจริง ๆ แล้วจะไม่ค่อยอยู่นิ่ง ๆ และบ่อยครั้งจะเปลี่ยนอย่างรวดเร็วมาก ยกตัวอย่างเช่น แม้เมื่อดูภาพนิ่ง มนุษย์มักขยับตาแบบ saccade ซึ่งก็คือการเปลี่ยนจุดที่มองอย่างรวดเร็ว ภาพซึ่งตกลงที่เซลล์รับแสงของจอตา ปกติจึงจะเปลี่ยนทุก ๆ ไม่กี่ร้อยมิลลิวินาที[19]
ถึงแม้จะมีข้อบกพร่องเช่นนี้ การเข้ารหัสแบบอัตรานับศักยะงาน ก็ไม่ได้ใช้เพียงแค่ในการทดลองเท่านั้น แต่ยังใช้ในแบบจำลองของโครงข่ายประสาทเทียมอีกด้วย เป็นวิธีที่ทำให้เข้าใจว่า เซลล์ประสาทจะเปลี่ยนข้อมูลเกี่ยวกับตัวแปรขาเข้าอย่างหนึ่ง (คือระดับสิ่งเร้า) ไปเป็นตัวแปรขาออกที่ต่อเนื่องอีกอย่างหนึ่ง (คืออัตราการยิงสัญญาณ)
แต่ก็มีหลักฐานที่เพิ่มขึ้นเรื่อย ๆ ว่า อย่างน้อยที่สุด เซลล์เพอร์คินจีในสมองน้อย ก็ไม่ได้เข้ารหัสข้อมูลด้วยอัตราการยิงสัญญาณเท่านั้น แต่ด้วยเมื่อไร (timing) และระยะ (duration) ที่ไม่ยิงสัญญาณคืออยู่เฉย ๆ ด้วย[20][21]
อัตราการยิงสัญญาณขึ้นอยู่กับเวลา (time-dependent firing rate)[แก้]
ส่วนนี้ไม่มีการอ้างอิงจากเอกสารอ้างอิงหรือแหล่งข้อมูล โปรดช่วยพัฒนาส่วนนี้โดยเพิ่มแหล่งข้อมูลน่าเชื่อถือ เนื้อหาที่ไม่มีการอ้างอิงอาจถูกคัดค้านหรือนำออก |
อัตราการยิงสัญญาณขึ้นอยู่กับเวลา (time-dependent firing rate) นิยามเป็น จำนวนการยิงศักยะงานโดยเฉลี่ย (เฉลี่ยตามการทดลองซ้ำ ๆ) ที่ปรากฏในช่วงเวลาสั้น ๆ ระหว่าง t และ t+Δt แล้วหารโดยช่วงระยะเวลา เป็นการวัดที่ใช้ได้ทั้งสิ่งเร้านิ่ง ๆ และสิ่งเร้าที่เปลี่ยนไปตามเวลา
เมื่อจะวัดค่าอัตราการยิงสัญญาณขึ้นอยู่กับเวลาในการทดลอง ผู้ทำการทดลองจะบันทึกค่าจากนิวรอนเมื่อเร้าด้วยสิ่งเร้าที่ทำเป็นชุด ๆ การเร้าเป็นชุดนี้จะทำซ้ำหลายครั้ง และการตอบสนองของนิวรอนจะบันทึกเป็น Peristimulus time histogram (PSTH) จุดเวลา t จะวัดจากเมื่อเริ่มเร้าด้วยชุดสิ่งเร้า ค่า Δt จะต้องใหญ่พอ (ปกติเริ่มจาก 1 มิลลิวินาทีขึ้น) เพื่อให้มีจำนวนศักยะงานพอประเมินค่าเฉลี่ยอย่างเชื่อถือได้ เมื่อหารด้วยระยะเวลา Δt ก็จะได้ค่า อัตราการยิงสัญญาณขึ้นอยู่กับเวลา r(t) ของนิวรอน ซึ่งเท่ากับความหนาแน่นของศักยะงาน (spike density) ใน PSTH
ถ้า Δt น้อยพอดี r(t) Δt ก็จะเป็นจำนวนศักยะงานโดยเฉลี่ยที่เกิดระหว่าง t จนถึง t+Δt ในการทดลองหลาย ๆ ครั้ง ถ้า Δt มีค่าน้อย ก็จะไม่มีศักยะงานเกินกว่า 1 ในระหว่าง t จนถึง t+Δt ในการทดลองทุกครั้ง ซึ่งก็หมายความว่า r(t) Δt ก็จะมีค่าเป็นเศษส่วนในการทดลองต่าง ๆ ที่บางการทดลองมีศักยะงานหนึ่งพัลส์ในช่วงเวลานั้น หรือโดยเสมอภาคกัน r(t) Δt ก็จะเป็นค่าความน่าจะเป็นที่ศักยะงานหนึ่ง ๆ จะเกิดในช่วงระยะเวลานี้
โดยเป็นวิธีดำเนินการทดลอง อัตราการยิงสัญญาณขึ้นอยู่กับเวลาจะมีประโยชน์เพื่อตรวจการทำงานของเซลล์ประสาท โดยเฉพาะในกรณีที่มีสิ่งเร้าซึ่งขึ้นอยู่กับเวลา ปัญหาโต้ง ๆ ของวิธีนี้ก็คือ มันไม่ใช่วิธีการเข้ารหัสของเซลล์ประสาทในสมอง เพราะมันไม่สามารถรอให้สิ่งเร้าแสดงตัวซ้ำ ๆ ในแบบที่ว่านี้ก่อนจะตอบสนอง
อย่างไรก็ดี ค่านี้จะมีเหตุผล ถ้ามีนิวรอนที่เป็นอิสระต่อกันและกันเป็นกลุ่มใหญ่ ๆ ที่ได้รับสิ่งเร้าเดียวกัน ดังนั้น แทนการบันทึกการตอบสนองจากกลุ่มเซลล์จำนวน N เซลล์ในการทดลองครั้งหนึ่ง การบันทึกการตอบสนองจากเซลล์เดียวแล้วหาค่าเฉลี่ยจากการทดลอง N ครั้ง ก็จะง่ายกว่า ดังนั้น ค่านี้จะมีข้อสมมุติโดยปริยายว่า จะเป็นนิวรอนเป็นกลุ่ม ๆ ที่ตอบสนอง
การเข้ารหัสโดยเวลา (Temporal coding)[แก้]
เมื่อเวลาที่ส่งศักยะงานหรือความผันผวนของการยิงสัญญาณที่อัตราสูงพบว่ามีข้อมูล รหัสทางประสาทนี้บ่อยครั้งจะกำหนดว่าการเข้ารหัสโดยเวลา (Temporal coding)[22] งานศึกษาจำนวนหนึ่งได้พบว่า รายละเอียดทางเวลาของรหัสอยู่ในระดับมิลลิวินาที ซึ่งแสดงว่า เวลาการส่งศักยะงานที่แม่นยำเป็นส่วนประกอบสำคัญของรหัสทางประสาท[3][23] การเข้ารหัสข้อมูลเช่นนี้ ซึ่งสื่อผ่านเวลาระหว่างพัลส์ศักยะงานจะเรียกว่า interpulse interval code และมีงานศึกษาจำนวนหนึ่งที่สนับสนุนให้หลักฐาน[24]
ความผันผวนเมื่อยิงสัญญาณที่อัตราสูงของนิวรอน อาจจะเป็นเสียงรบกวนหรืออาจจะเป็นข้อมูลก็ได้ แบบจำลองการเข้ารหัสโดยอัตราเสนอว่า ความไม่สม่ำเสมอเช่นนี้เป็นเสียงรบกวน ส่วนแบบจำลองการเข้ารหัสโดยเวลาเสนอว่า มันเป็นข้อมูล ถ้าระบบประสาทใช้แค่รหัสโดยอัตราเพื่อสื่อข้อมูล อัตราการยิงสัญญาณที่สม่ำเสมอปกติยิ่งกว่านี้ก็ควรจะเป็นข้อได้เปรียบทางวิวัฒนาการ และนิวรอนก็ควรใช้วิธีการนี้และหลีกเลี่ยงวิธีการอื่นที่ไม่ทนเสียงรบกวนเท่า[25]
รหัสโดยเวลาให้คำอธิบายอีกอย่างเกี่ยวกับ "เสียงรบกวน" ว่าเป็นการเข้ารหัสข้อมูลและมีผลต่อการประมวลข้อมูล เพื่อจะจำลองไอเดียนี้ เลขฐานสองสามารถใช้กำหนดช่วงศักยะงาน โดย 1 หมายถึงมีศักยะงาน และ 0 หมายถึงไม่มี รหัสโดยเวลาจะอนุญาตให้ลำดับ 000111000111 มีความหมายต่างจากลำดับ 001100110011 แม้อัตราการยิงสัญญาณของลำดับสองชุดนี้จะเท่ากัน คือ 6 ศักยะงานต่อ/10 มิลลิวินาที[26]
จนกระทั่งเร็ว ๆ นี้ นักวิทยาศาสตร์ปกติจะใช้รหัสโดยอัตราเพื่ออธิบายรูปแบบกระแสประสาทที่เห็นหลังไซแนปส์ (post-synaptic) แต่การทำงานของสมองดูจะต้องแม่นยำตามกาลเวลา เกินกว่าที่รหัสโดยอัตราเพียงอย่างเดียวจะสามารถรองรับได้[ต้องการอ้างอิง] กล่าวอีกอย่างก็คือ ข้อมูลสำคัญอาจสูญไปได้เพราะรหัสโดยอัตราไม่สามารถเก็บข้อมูลที่มีทั้งหมดจากขบวนศักยะงาน นอกจากนั้น การตอบสนองจะต่างกันพอสมควรระหว่างสิ่งเร้าที่คล้าย (แต่ไม่เหมือนกัน) ซึ่งแสดงว่า รูปแบบที่ไม่เหมือนกันต่าง ๆ ของขบวนศักยะงานจะมีข้อมูลมากกว่าที่เป็นไปได้ถ้าเป็นรหัสโดยอัตรา[27]
รหัสโดยเวลาจะรวมลักษณะต่าง ๆ ของศักยะงานที่การเข้ารหัสโดยอัตราไม่ได้รวม ยกตัวอย่างเช่น เวลาก่อนเกิดศักยะงานแรกหลังจากที่ได้สิ่งเร้า, ลักษณะต่าง ๆ ที่ขึ้นกับโมเมนต์ทางสถิติที่สองหรือยิ่งกว่านั้นของการแจกแจงความน่าจะเป็นของช่วงระหว่างสิ่งเร้า (Interstimulus interval), ความสุ่มของศักยะงาน, หรือกลุ่มศักยะงานที่ยิงในเวลาที่แม่นยำ (เป็นรูปแบบทางกาลเวลา) ล้วนแต่เป็นข้อมูลที่สามารถใช้เข้ารหัสโดยเวลา[28]
เนื่องจากไม่มีแหล่งอ้างอิงเวลาแบบสัมบูรณ์ภายในระบบประสาท ข้อมูลก็จะต้องเกี่ยวข้องกับเวลาการเกิดศักยะงานโดยเปรียบเทียบภายในกลุ่มนิวรอน หรือกับการแกว่งกวัดของคลื่นสมอง[3][5] วิธีถอดรหัสโดยเวลาอย่างหนึ่งเมื่อมีการแกว่งกวัดของคลื่นสมอง ก็คือศักยะงานที่ยิงในคาบโดยเฉพาะ ๆ ของวงจรการกวัดแว่ง จะทำให้นิวรอนหลังไซแนปส์ลดขั้วอย่างมีประสิทธิภาพกว่า[29]
โครงสร้างทางเวลาของขบวนศักยะงาน หรืออัตราการยิงสัญญาณ จะกำหนดโดยทั้งการเปลี่ยนแปลงของสิ่งเร้าและกระบวนการเข้ารหัสของนิวรอนเอง สิ่งเร้าที่เปลี่ยนแปลงอย่างรวดเร็วมักจะสร้างขบวนศักยะงานที่มีลักษณะทางเวลาที่แม่นยำและอัตราการยิงสัญญาณที่เปลี่ยนอย่างรวดเร็ว ไม่ว่าระบบจะใช้รหัสอะไรก็ตาม รหัสโดยเวลาจะส่องรายละเอียดทางเวลาในการตอบสนองที่ไม่ได้เกิดจากความเปลี่ยนแปลงของสิ่งเร้าเท่านั้น แต่จะสัมพันธ์กับลักษณะต่าง ๆ ของสิ่งเร้าด้วย ปฏิสัมพันธ์ระหว่างสิ่งเร้าและพลวัตของการเข้ารหัส ทำให้ระบุรหัสโดยเวลาได้ยาก
เนื่องกับรหัสทางเวลา การเรียนรู้จะเกิดผ่านการปรับความช้าเร็วของการสื่อผ่านไซแนปส์โดยขึ้นอยู่กับการทำงาน (activity-dependent synaptic delay modifications)[30] การปรับเปลี่ยนเองก็จะต้องขึ้นกับไม่ใช่เพียงแค่อัตราการยิงสัญญาณ (คือรหัสโดยอัตรา) แต่จะขึ้นกับรูปแบบทางกาลเวลาของศักยะงานด้วย (คือรหัสโดยเวลา) คือ นี่อาจเป็นกรณีพิเศษของกระบวนการ spike-timing-dependent plasticity[31]
ปัญหาของการเข้ารหัสโดยเวลา จะต่างอย่างเป็นอิสระจากปัญหาการเข้ารหัสศักยะงานแต่ละพัลส์ ๆ ที่เป็นอิสระจากกันและกัน ถ้าศักยะงานแต่ละพัลส์เป็นอิสระจากพัลส์อื่น ๆ ในขบวน คุณสมบัติทางเวลาของรหัสประสาทจะกำหนดได้โดยอัตราการยิงสัญญาณที่ขึ้นอยู่กับเวลา r(t) และถ้า r(t) เปลี่ยนช้า ๆ ไปตามเวลา นี่ก็เท่ากับการเข้ารหัสโดยอัตรา แต่ถ้าเปลี่ยนไปอย่างรวดเร็ว นี่เป็นการเข้ารหัสโดยเวลา
การเข้ารหัสโดยเวลาในระบบรับความรู้สึก[แก้]
สำหรับสิ่งเร้าสั้น ๆ อัตราการยิงศักยะงานสูงสุดของเซลล์ประสาทอาจไม่เร็วพอจะสร้างศักยะงานมากกว่าพัลส์เดียว เนื่องจากมีข้อมูลมากเกี่ยวกับสิ่งเร้าสั้น ๆ ภายในศักยะงานเดียวนี้ จึงดูเหมือนว่าเวลาการยิงศักยะงานเองจะต้องสื่อข้อมูลมากกว่าเพียงเป็นความถี่เฉลี่ยของจำนวนศักยะงานตามระยะเวลา
แบบจำลองนี้สำคัญมากในเรื่องการกำหนดตำแหน่งต้นเสียง (sound localization) ซึ่งเกิดในสมองภายในมิลลิวินาที ๆ คือสมองจะต้องดึงข้อมูลมหาศาลจากการตอบสนองค่อนข้างสั้น ๆ ของเซลล์ประสาท นอกจากนั้น ถ้าการยิงสัญญาณในอัตราที่ต่ำเพียงเป็นสิบ ๆ พัลส์ต่อวินาที จะต้องจำแนกจากอัตราที่ใกล้ ๆ กันสำหรับสิ่งเร้าที่ต่างกัน เซลล์ประสาทที่ต้องจำแนกสิ่งเร้าที่ต่างสองอย่างนี้ ก็จะต้องรอหนึ่งวินาทีหรือมากกว่านั้นเพื่อรวบรวมข้อมูลจนเพียงพอ ซึ่งไม่สอดคล้องกับสิ่งมีชีวิตเป็นจำนวนมากที่สามารถจำแนกสิ่งเร้าสองอย่างที่ว่าได้โดยใช้เวลาแค่เป็นมิลลิวินาที ๆ นี่แสดงว่าระบบประสาทไม่ได้ใช้การเข้ารหัสโดยอัตราเพียงอย่างเดียว[26]
เพื่ออธิบายการเข้ารหัสสิ่งเร้าทางตาได้อย่างรวดเร็ว จึงมีการเสนอว่า เซลล์ประสาทในจอตาจะเข้ารหัสข้อมูลเป็นระยะเวลาแฝงระหว่างการเริ่มมีสิ่งเร้ากับการเกิดศักยะงานแรก ซึ่งเรียกว่า latency to first spike[32] โดยรหัสเช่นนี้ก็พบด้วยในระบบการได้ยินและระบบรับความรู้สึกทางกาย ข้อเสียหลักของรหัสนี้ก็คือจะอ่อนไหวต่อความผันผวนของเซลล์ประสาทที่มีอยู่ตามธรรมชาติ[33]
ในคอร์เทกซ์การมองเห็นปฐมภูมิของลิงมาคาก เวลาระหว่างศักยะงานแรกกับการเริ่มมีสิ่งเร้าพบว่า ให้ข้อมูลมากกว่าระยะเวลาระหว่างศักยะงานเอง แต่เวลาระหว่างศักยะงานก็ยังสามารถใช้เข้ารหัสข้อมูลอื่น ๆ และสำคัญเป็นพิเศษเมื่ออัตราการส่งสัญญาณถึงจุดยอด เช่นเมื่อสิ่งที่เห็นมีความเปรียบต่างสูง ด้วยเหตุนี้ รหัสโดยเวลาอาจมีบทบาทในการเข้ารหัสส่วนขอบของสิ่งที่เห็น (ที่มีความเปรียบต่างสูง) และไม่มีเมื่อสิ่งเร้าเปลี่ยนอย่างอย่างช้า ๆ หรือน้อย[34]
ระบบรู้รสของสัตว์เลี้ยงลูกด้วยนมช่วยในการศึกษารหัสโดยเวลา เพราะสิ่งเร้าค่อนข้างต่าง ๆ กัน และสัตว์ก็ตอบสนองต่าง ๆ กันพอสังเกตได้[35] ข้อมูลที่เข้ารหัสโดยเวลาอาจช่วยสิ่งมีชีวิตให้จำแนกรสชาติต่าง ๆ ที่อยู่ในหมวดเดียวกัน (เช่น หวาน ขม เปรี้ยว เค็ม อุมะมิ) แม้อัตราศักยะงานจะเหมือนกัน ข้อมูลทางเวลาของรูปแบบการตอบสนองต่อรสชาติแต่ละอย่าง อาจใช้ระบุว่ามันคืออะไร (เช่น ความแตกต่างระหว่างรสขมสองอย่าง เช่นยาควินินและ Denatonium ที่ขมมาก) ดังนั้น ทั้งการเข้ารหัสโดยอัตราและโดยเวลาอาจจะใช้ในระบบรู้รส คือโดยอัตราสำหรับหมวดหมู่พื้นฐานของรสชาติ และโดยเวลาสำหรับรายละเอียดโดยเฉพาะอื่น ๆ[36]
งานวิจัยในระบบรู้รสของสัตว์เลี้ยงลูกด้วยนมได้แสดงว่า มีข้อมูลจำนวนมากในรูปแบบตามกาลเวลาที่ใช้ในกลุ่มเซลล์ประสาทต่าง ๆ และเป็นข้อมูลที่ต่างจากที่เข้ารหัสโดยอัตรา กลุ่มเซลล์ประสาทอาจประสานส่งกระแสประสาทพร้อม ๆ กันเมื่อตอบสนองต่อสิ่งเร้าหนึ่ง ๆ
ในการศึกษาสมองกลีบหน้าของไพรเมต รูปแบบทางเวลาที่ละเอียดแม่นยำเป็นระยะเวลาสั้น ๆ เพียงไม่กี่มิลลิวินาทีจะพบทั่วกลุ่มเซลล์ประสาท ซึ่งมีสหสัมพันธ์กับพฤติกรรมเกี่ยวกับการแปลข้อมูลบางอย่าง แม้นักวิทยาศาสตร์ยังกำหนดรายละเอียดไม่ค่อยได้ แต่ก็อาจอธิบายได้ว่า เป็นผลพลอยได้ในระบบต่าง ๆ ของเปลือกสมองที่ใช้ข้อมูลขาเข้าร่วมกัน หรืออาจเพื่อเพิ่มความเร็วในการแปลผลของเปลือกสมองโดยไม่ได้ข้อมูลอะไรเพิ่ม[37]
เหมือนกับระบบการเห็น ใน mitral cell ของป่องรับกลิ่นในหนูหริ่ง ระยะเวลาของศักยะงานแรกจากการดมกลิ่น (คือระยะแฝง) ดูเหมือนจะเข้ารหัสข้อมูลจำนวนมากเกี่ยวกับกลิ่น กลยุทธ์การใช้ระยะแฝงทำให้สามารถระบุกลิ่นและมีพฤติกรรมตอบสนองต่อกลิ่นนั้นได้เร็ว นอกจากนั้น mitral cell ยังมีรูปแบบการส่งสัญญาณโดยเฉพาะ ๆ ต่อกลิ่นต่าง ๆ ข้อมูลเช่นนี้อาจช่วยระบุกลิ่นบางชนิด แต่อาจไม่จำเป็นต้องมี เพราะอัตราของศักยะงานในช่วงที่สัตว์ดมกลิ่นก็สามารถทำให้ระบุกลิ่นได้แล้ว[38]
ในแนวเดียวกัน งานทดลองในระบบรู้กลิ่นของกระต่ายแสดงการส่งสัญญาณในรูปแบบต่าง ๆ ที่มีสหสัมพันธ์กับกลิ่นต่าง ๆ และก็พบผลเช่นเดียวกันในงานทดลองกับตั๊กแตน[26]
การประยุกต์ใช้[แก้]
ความจำเพาะเจาะจงของรหัสโดยเวลา ทำให้ต้องใช้เทคโนโลยีที่ละเอียดมากในการวัดหาข้อมูลทางการทดลองที่ทั้งให้ความรู้และเชื่อถือได้ ความก้าวหน้าทางเทคนิค optogenetics ช่วยให้นักประสาทวิทยาศาสตร์สามารถควบคุมศักยะงานภายในนิวรอนหนึ่ง ๆ ได้โดยเฉพาะ ทำให้ควบคุมรูปแบบไฟฟ้าของศักยะงานและระยะเวลาระหว่างศักยะงานในระดับเซลล์เดี่ยว ๆ ได้ ยกตัวอย่างเช่น แสงสีน้ำเงินจะทำให้ช่องไอออนเปิดปิดด้วยแสง คือ channelrhodopsin เปิด ทำให้เซลล์ลดขั้วแล้วสร้างศักยะงาน เมื่อเซลล์ตรวจไม่พบแสงสีน้ำเงินอีก ช่องก็จะปิด แล้วเซลล์ก็จะหยุดส่งศักยะงาน รูปแบบของศักยะงานจะจับคู่กับรูปแบบของสิ่งเร้าคือแสงสีน้ำเงิน การใส่ลำดับยีนของ channelrhodopsin เข้าในดีเอ็นเอของหนูหริ่ง จึงทำให้นักวิจัยสามารถควบคุมศักยะงานและควบคุมพฤติกรรมบางอย่างของหนู (เช่น ทำให้หนูหันไปทางซ้าย) ได้[39] ผ่านเทคนิค optogenetics นักวิจัยจึงมีอุปกรณ์ที่สร้างผลต่อการเข้ารหัสโดยเวลาต่าง ๆ ในนิวรอน ในขณะที่ยังดำรงอัตราเฉลี่ยการยิงสัญญาณเท่า ๆ กัน และดังนั้น จึงสามารถทดสอบได้ว่า มีวงจรประสาทหนึ่ง ๆ ที่เข้ารหัสโดยเวลาหรือไม่[40]
เทคโนโลยี Optogenetic มีโอกาสช่วยแก้ปัญหาการส่งศักยะงานที่เป็นมูลฐานของโรคทางประสาทและจิตหลายอย่าง[40] ถ้าจริง ๆ นิวรอนเข้ารหัสข้อมูลในรูปแบบตามเวลาของศักยะงาน ข้อมูลสำคัญอาจจะมองข้ามไปเมื่อพยายามถอดรหัสจากแค่อัตราการยิงสัญญาณ[26] การเข้าใจรหัสประสาทในรูปแบบตามเวลาและการทำซ้ำรูปแบบเหล่านี้ได้ในนิวรอน อาจจะทำให้ควบคุมและรักษาโรคในระบบประสาท เช่น โรคซึมเศร้า โรคจิตเภท และโรคพาร์คินสัน ได้ดีขึ้น เพราะการควบคุมระยะการส่งศักยะงานในเซลล์เดี่ยว ๆ จะทำให้ควบคุมการทำงานของสมองได้แม่นยำยิ่งกว่าการใช้ยา[39]
การเข้ารหัสโดยเฟสที่ยิงสัญญาณ (Phase-of-firing code)[แก้]
รหัสโดยเฟสที่ยิงสัญญาณ (Phase-of-firing code) เป็นรหัสทางประสาทที่รวมการเข้ารหัสโดยอัตรา กับจุดอ้างอิงทางเวลาซึ่งอาศัยการแกว่งกวัดของคลื่นสมอง (Neural oscillation) รหัสประเภทนี้มีป้าย/ข้อมูลเวลาสำหรับแต่ละศักยะงานโดยอ้างอิงเวลาตามเฟสการแกว่งกวัดของคลื่นประสาทเฉพาะที่ ๆ ไม่ว่าจะแบบความถี่ต่ำ[41] หรือความถี่สูง[42] ลักษณะอย่างหนึ่งของการเข้ารหัสนี้ก็คือ นิวรอนจะมีลำดับการยิงสัญญาณโดยเฉพาะ ๆ[43]
มีงานศึกษาที่แสดงว่า นิวรอนในเปลือกสมองรับความรู้สึกบางส่วน เข้ารหัสสิ่งเร้าที่ซับซ้อนตามธรรมชาติโดยเวลาของศักยะงานที่เป็นไปตามเฟสของคลื่นสมองในพื้นที่ ไม่ใช่เป็นไปตามจำนวนศักยะงานเท่านั้น[41][44] โดยคลื่นสมองจะสะท้อนศักย์สนามไฟฟ้าเฉพาะที่ (local field potential) นี่บ่อยครั้งจัดเป็นรหัสโดยเวลาแม้ป้ายเวลาที่ใช้กับศักยะงานจะค่อนข้างหยาบ
นั่นก็คือ ค่าวิยุต 4 ค่าสำหรับเฟสต่าง ๆ ก็พอใช้เป็นตัวแทนข้อมูลที่อยู่ในรหัสเช่นนี้ โดยหมายเอาเฟสของการกวัดแกว่งที่ความถี่ต่ำ รหัสโดยเฟสที่ยิงสัญญาณได้ไอเดียคร่าว ๆ จากปรากฏการณ์ Phase precession ใน place cell (เซลล์สถานที่) ที่ฮิปโปแคมปัส ซึ่งเป็นเซลล์ที่ทำงานเมื่อสัตว์ไปถึงสถานที่โดยเฉพาะ ๆ ภายในสิ่งแวดล้อม
การเข้ารหัสตามเฟสยังพบในเปลือกสมองส่วนการเห็นที่มีการกวัดแกว่งความถี่สูงด้วย[43] ภายในรอบของการกวัดแกว่งพิสัยแกมมา (30-70&npbs;เฮิรตซ์) เซลล์ประสาทแต่ละตัวจะมีช่วงที่มักจะยิงสัญญาณ เพราะเหตุนี้ กลุ่มนิวรอนทั้งหมดจึงสร้างขบวนศักยะงานที่มีระยะยาวถึงประมาณ 15 มิลลิวินาที[43]
การเข้ารหัสโดยกลุ่ม (Population coding)[แก้]
การเข้ารหัสโดยกลุ่ม (Population coding) เป็นวิธีเข้ารหัสสิ่งเร้าโดยการทำงานร่วมกันของนิวรอนจำนวณหนึ่ง ในวิธีนี้ นิวรอนแต่ละเซลล์จะตอบสนองต่อสิ่งเร้าบางเซตแบบกระจายตัว และการตอบสนองของนิวรอนจำนวนหนึ่งรวมกันก็จะสามารถกำหนดค่าบางอย่างเกี่ยวกับสิ่งเร้า
จากมุมมองทางทฤษฎี การเข้ารหัสโดยกลุ่มเป็นเรื่องที่เข้าสูตรทางคณิตได้ค่อนข้างดีในบรรดาปัญหาทางประสาทวิทยาศาสตร์ทั้งหลาย มันรวมส่วนสำคัญต่าง ๆ ของการเข้ารหัสทางประสาท แต่ก็ยังวิเคราะห์ทางทฤษฎีได้ง่ายพอ[45] งานศึกษาแบบทดลองได้แสดงว่า การเข้ารหัสแบบนี้ใช้อย่างกว้างขวางภายในเขตสมองส่วนรับความรู้สึก (sensory) และส่วนสั่งการ (motor)
ยกตัวอย่างเช่น ในเขตการเห็นของสมองกลีบขมับส่วนใน (Medial temporal lobe, MT) นิวรอนจะประมวลผลกำหนดโดยทิศทางที่สิ่งเร้าเคลื่อนที่โดยเฉพาะ ๆ.[46] ในการตอบสนองต่อวัตถุที่กำลังเคลื่อนที่ไปยังทิศทางหนึ่งโดยเฉพาะ ๆ นิวรอนจำนวนมากใน MT จะยิงสัญญาณแบบมีเสียงรบกวน โดยมีรูปแบบเป็นระฆังคว่ำตลอดทั้งกลุ่ม แต่ทิศทางของวัตถุก็ยังสามารถกำหนดได้จากการทำงานของนิวรอนทั้งกลุ่ม ซึ่งทนต่อความผันผวนของสัญญาณจากนิวรอนเดี่ยว ๆ
ในตัวอย่างคลาสสิกตัวอย่างหนึ่งใน primary motor cortex นักวิจัยได้ฝึกลิงให้ขยับก้านควบคุมไปยังเป้าหมาย[47][48] แล้วพบว่า นิวรอนหนึ่ง ๆ จะยิงสัญญาณตอบสนองต่อทิศทางการเคลื่อนที่ของเป้าหมายหลายทิศทาง แต่มันจะยิงสัญญาณที่อัตราสูงสุดในทิศทางเดียว และที่อัตราลดลงขึ้นอยู่กับว่า ทิศทางของเป้าหมายนั้นใกล้กับทิศทางซึ่งมันถนัดที่สุดมากเท่าไร
นักวิชาการคนหนึ่ง (Kenneth Johnson) ได้สรุปว่า ถ้านิวรอนแต่ละตัวเป็นตัวแทนการเคลื่อนไหวของสิ่งเร้าในทิศทางที่ตนถนัด การคำนวณรวมเวกเตอร์ของนิวรอนทั้งหมด โดยนิวรอนแต่ละตัวมีอัตราการยิงสัญญาณและทิศทางที่ตนถนัดโดยเฉพาะ ๆ ก็จะแสดงทิศทางการเคลื่อนที่ของสิ่งเร้า ดังนั้น การทำงานของกลุ่มนิวรอนจึงเข้ารหัสทิศทางการเคลื่อนที่ของสิ่งเร้า การเข้ารหัสเช่นนี้มีชื่อเฉพาะว่า population vector coding[ต้องการอ้างอิง]
นักวิชาการอีกลุ่มหนึ่งได้พัฒนารหัสโดยกลุ่มตามสถานที่-เวลา ซึ่งเรียกว่า Averaged-Localized-Synchronized-Response (ALSR) code โดยเป็นการเข้ารหัสสิ่งเร้าทางหูคือเสียง และใช้ข้อมูลเกี่ยวกับนิวรอนที่ตอบสนองต่อจุดที่เป็นแหล่งเสียงโดยเฉพาะ ๆ ในโสตประสาท (auditory nerve) กับการยิงสัญญาณจับคู่กับเฟสภายในโสตประสาท การเข้ารหัสดั้งเดิมใช้ได้กับเสียงสระแบบไม่เปลี่ยนเสียง[49] ต่อมาจึงใช้ได้กับพยางค์ที่ประกอบด้วยพยัญชนะ-สระ โดยรวมความสูงต่ำของเสียง (pitch) และความถี่สั่นพ้อง (formant) ที่ซับซ้อนและอาจเปลี่ยนเสียงในระหว่าง (non steady state)[50][51]
การเข้ารหัสโดยกลุ่มยังมีข้อดีอื่น ๆ อีกด้วย รวมทั้งการลดความไม่แน่นอนเนื่องจากความผันแปรได้ทางสถิติ และสมรรถภาพในการเป็นตัวแทนลักษณะสิ่งเร้าต่าง ๆ พร้อม ๆ กัน วิธีนี้ยังเร็วกว่าการเข้ารหัสโดยอัตรา และสามารถสะท้อนความเปลี่ยนแปลงของสิ่งเร้าได้แทบทันที[52] นิวรอนแต่ละตัวในกลุ่มมักจะตอบสนองสิ่งเร้าที่ต่าง ๆ แต่คาบเกี่ยวกัน ดังนั้น นิวรอนจำนวนหนึ่งแต่ไม่ทั้งหมดก็จะตอบสิ่งเร้าหนึ่ง ๆ
โดยปกติแล้ว ฟังก์ชันการเข้ารหัสจะมีค่าสูงสุด เมื่อการทำงานของนิวรอนนั้น ๆ อยู่ในระดับสูงสุด และก็จะลดลงตามลำดับค่าที่ไม่ใช่เป็นจุดยอด[ต้องการอ้างอิง] ดังนั้น ระดับการรับรู้สิ่งเร้าจึงสามารถคำนวณได้จากรูปแบบการทำงานทั่วไปของกลุ่มนิวรอน
population vector coding ที่กล่าวถึงมาก่อนเป็นตัวอย่างของการหาค่าเฉลี่ยธรรมดา ๆ เทคนิคทางคณิตศาสตร์ที่ซับซ้อนกว่ารวมวิธีค่าควรจะเป็นสูงสุด (maximum likelihood) อาศัยการแจกแจงหลายตัวแปร (multivariate distribution) ของการตอบสนองของนิวรอน แบบจำลองเหล่านี้อาจสมมุติความเป็นอิสระ หรือสหสัมพันธ์แบบทุติยภูมิ[53] หรือแม้แต่ภาวะพึ่งพิงที่ซับซ้อนอย่างเช่น higher order maximum entropy probability distribution[54] หรือ Copula[55]
การเข้ารหัสโดยสหสัมพันธ์ (Correlation coding)[แก้]
แบบจำลองการเข้ารหัสโดยสหสัมพันธ์เสนอว่า มีสหสัมพันธ์ระหว่างศักยะงานภายในขบวน ซึ่งอาจเป็นข้อมูลนอกเหนือไปจากระยะเวลาธรรมดาระหว่างศักยะงานต่าง ๆ งานวิจัยปี 2523 แสดงว่า สหสัมพันธ์ระหว่างขบวนศักยะงานจะสามารถลด แต่ไม่สามารถเพิ่มข้อมูลที่พึ่งพาอาศัยกัน (mutual information) ที่มีในขบวนศักยะงาน 2 ขบวน โดยเกี่ยวกับลักษณะหนึ่งของสิ่งเร้า[56] แต่งานปี 2542 แสดงว่าไอเดียนี้ไม่ถูกต้อง โครงสร้างโดยสหสัมพันธ์จะสามารถเพิ่มข้อมูลที่มี ถ้าค่าสหสัมพันธ์ของเสียงรบกวนและของสัญญาณ/ข้อมูลมีเครื่องหมายตรงกันข้ามกัน[57]
ค่าสหสัมพันธ์สามารถให้ข้อมูลที่ไม่ได้อยู่ในอัตราการยิงสัญญาณโดยเฉลี่ยของนิวรอนสองคู่ ตัวอย่างหนึ่งก็คือ เปลือกสมองส่วนการได้ยินของมาโมเสทที่ได้ยาชาแล้ว ซึ่งเสียงโทนเดียวจะทำให้เกิดศักยะงานที่มีสหสัมพันธ์กันจำนวนมากขึ้น แต่ก็ไม่ได้เพิ่มอัตราการยิงสัญญาณโดยเฉลี่ยระหว่างนิวรอนเป็นคู่ ๆ[58]
การเข้ารหัสโดยศักยะงานอิสระ (Independent-spike coding)[แก้]
แบบจำลองการเข้ารหัสโดยศักยะงานอิสระเสนอว่า ศักยะงานแต่ละพัลส์เป็นอิสระจากกันและกันภายในขบวนศักยะงาน[59][60]
การเข้ารหัสโดยตำแหน่ง (Position coding)[แก้]


การเข้ารหัสโดยกลุ่มปกติจะเกี่ยวกับกลุ่มเซลล์ประสาทที่ตอบสนองโดยมี tuning curve เป็นฟังก์ชัน Gaussian ที่มีค่าคาดหมายหรือค่าเฉลี่ยซึ่งแปรผันแบบเชิงเส้นตามระดับสิ่งเร้า ซึ่งหมายความว่า เซลล์จะตอบสนองด้วยศักยะงานในอัตราสูงสุดต่อสิ่งเร้าที่มีระดับใกล้กับค่าคาดหมาย ดังนั้น ระดับของสิ่งเร้าจึงสามารถหาได้จากค่าคาดหมายของเซลล์ประสาทที่ตอบสนองในระดับสูงสุด แต่เพราะเสียงรบกวนที่มีโดยธรรมชาติในการตอบสนอง การประมาณค่าควรจะเป็นสูงสุด (maximum likelihood estimation) จะเป็นวิธีที่แม่นยำกว่า
การเข้ารหัสเช่นนี้จะใช้สำหรับตัวแปรแบบต่อเนื่องเช่น ตำแหน่งข้อต่อ ตำแหน่งตา สี หรือความถี่เสียง แม้นิวรอนเดี่ยว ๆ จะสร้างเสียงรบกวนมากเกินกว่าจะสามารถเข้ารหัสตัวแปรโดยอัตรา แต่กลุ่มนิวรอนรวมกันก็สามารถให้ข้อมูลที่เชื่อถือได้และแม่นยำกว่า สำหรับกลุ่มนิวรอนที่มี tuning curve แบบมียอดเดียว ความแม่นยำปกติจะดีขึ้นในเชิงเส้นตามจำนวนของเซลล์ประสาท ดังนั้น สำหรับความแม่นยำครึ่งหนึ่ง ก็จะใช้นิวรอนจำนวนครึ่งเดียว เทียบกับ tuning curve แบบมีหลายยอด ดังที่พบใน grid cell ในสมองของสัตว์หลายสปีชีส์ เป็นเซลล์ซึ่งเข้ารหัสข้อมูลเกี่ยวกับปริภูมิรอบ ๆ ตัวสัตว์ ความแม่นยำที่ได้จากกลุ่มนิวรอนเช่นนี้ จะเพิ่มขึ้นแบบยกกำลังตามจำนวนเซลล์ประสาท ซึ่งลดจำนวนนิวรอนได้อย่างมหาศาลเพื่อให้ได้ความแม่นยำเท่ากัน[61]
การเข้ารหัสแบบน้อยเซลล์ (Sparse coding)[แก้]
การเข้ารหัสแบบน้อยเซลล์ก็คือลักษณะสิ่งเร้าแต่ละอย่างจะเข้ารหัสโดยการทำงานอย่างเต็มที่ของนิวรอนเป็นจำนวนน้อย คือ จะมีกลุ่มนิวรอนย่อย ๆ ที่ทำงานตอบสนองต่อลักษณะสิ่งเร้าที่ต่างกัน
ถึงกระนั้น "ความน้อย" ก็อาจจะเป็นทางเวลา คือ "จะทำงานเป็นช่วงเวลาค่อนข้างน้อย" หรืออาจจะหมายถึงจำนวนนิวรอนที่ทำงานตอบสนองภายในกลุ่ม ในกรณีหลัง จึงอาจนิยามได้ว่าเป็นจำนวนนิวรอนที่ทำงานเปรียบเทียบกับจำนวนนิวรอนทั้งหมดภายในกลุ่มในช่วงระยะเวลาหนึ่ง นี่ดูเหมือนจะเป็นเอกลักษณ์ของการแปลผลทางประสาทเมื่อเปรียบเทียบกับคอมพิวเตอร์ดั้งเดิม เพราะข้อมูลจะกระจายตัวไปอย่างกว้างขวางไปทั่วกลุ่มนิวรอน งานวิจัยปี 2539 แสดงว่า[62] การเข้ารหัสแบบน้อยเซลล์ของรูปภาพต่าง ๆ ตามธรรมชาติ จะสร้างฟิลเตอร์คล้ายกับ wavelet ซึ่งก็คล้ายกับลานรับสัญญาณของเซลล์ธรรมดา ๆ ในเปลือกสมองส่วนการเห็น ความจุของการเข้ารหัสเช่นนี้อาจเพิ่มโดยใช้การเข้ารหัสโดยเวลาพร้อม ๆ กัน ดังที่พบในระบบรู้กลิ่นของตั๊กแตน[63]
เพราะสิ่งเร้ามีรูปแบบต่าง ๆ มากมาย ขั้นตอนวิธีการเข้ารหัสแบบน้อยเซลล์จะพยายามสืบหารูปแบบจำนวนน้อยที่เป็นตัวแทน (representative patterns) อย่างอัตโนมัติ ซึ่งเมื่อรวมรูปแบบในสัดส่วนที่ถูกต้อง ก็จะสามารถเป็นตัวแทนของสิ่งเร้าที่ปรากฏ ดังนั้น รหัสโดยน้อยเซลล์ของสิ่งเร้าก็คือรูปแบบที่เป็นตัวแทนเหล่านี้ ยกตัวอย่างเช่น ประโยคมากมายในภาษาไทยสามารถเข้ารหัสเป็นเครื่องหมายต่าง ๆ ซึ่งมีจำนวนน้อย (เช่น อักษร วรรณยุกต์ ตัวเลข และวรรค) โดยรวมกันเป็นลำดับอย่างเฉพาะเจาะจงเพื่อเป็นตัวแทนประโยคหนึ่ง ๆ ในนัยเดียวกัน การเข้ารหัสแบบน้อยเซลล์ก็จะเป็นเหมือนกับเครื่องหมายเหล่านี้
Linear generative model[แก้]
แบบจำลองของการเข้ารหัสแบบน้อยเซลล์มักจะเป็นแบบ linear generative model (แบบจำลองเพิ่มพูนเชิงเส้น)[64] ในแบบจำลองนี้ เครื่องหมายจะรวมกันแบบผลรวมเชิงเส้นเพื่อประมาณข้อมูลขาเข้า
โดยรูปนัยก็คือ สำหรับเซตเวกเตอร์จำนวนจริงที่เป็นข้อมูลเข้าและมีมิติ k (k-dimensional set of real-numbered input vectors) คือ
เป้าหมายของการเข้ารหัสโดยน้อยเซลล์ก็คือเพื่อกำหนดเวกเตอร์ฐานหลักที่มีมิติ k และมีจำนวน n (n k-dimensional basis vectors) คือ พร้อมกับเวก์เตอร์มากเลขศูนย์ที่มีมิติ n (sparse n-dimensional vector) เวกเตอร์หนึ่ง ที่เป็นน้ำหนักหรือสัมประสิทธิ์สำหรับแต่ละเวกเตอร์ขาเข้า เพื่อให้ผลรวมเชิงเส้นของเวกเตอร์ฐานหลักในสัดส่วนที่กำหนดโดยสัมประสิทธิ์ มีผลเป็นค่าใกล้ ๆ กับเวกเตอร์ขาเข้า คือ [65]
รหัสที่สร้างโดยขั้นตอนวิธีที่ดำเนินการด้วย linear generative model อาจจัดเป็นสองอย่างคือแบบ soft sparseness (น้อยผ่อน ๆ) และ hard sparseness (น้อยจริง ๆ)[64] โดยแบบ 2 อย่างจะมุ่งหมายการกระจายตัวของสัมประสิทธิ์ของเวกเตอร์ฐานหลักสำหรับข้อมูลเข้าทั่วไป
- รหัสแบบน้อยผ่อน ๆ จะมีการกระจายตัวคล้าย Gaussian เรียบ ๆ แม้จะแหลมกว่าเส้นโค้ง Gaussian โดยมีค่า 0 มาก, มีค่าสัมบูรณ์ต่ำ ๆ บ้าง, มีค่าสัมบูรณ์สูง ๆ น้อยกว่า, และมีความสัมบูรณ์สูงมากน้อยมาก ดังนั้น เวกเตอร์ฐานหลักจำนวนมากจึงไม่ใช่ศูนย์คือยังให้ผลอยู่
- เทียบกับรหัสแบบน้อยจริง ๆ ซึ่งมีค่า 0 มาก, ไม่มีหรือเกือบไม่มีค่าสมบูรณ์ต่ำ, มีค่าสัมบูรณ์ที่มากขึ้นน้อยกว่า, และมีค่าสัมบูรณ์สูงมากน้อยมาก ดังนั้น เวกเตอร์ฐานหลักจำนวนน้อยมากก็จะมีค่ามากกว่า 0 ซึ่งได้เปรียบจากมุมมองของเมแทบอลิซึม เพราะการทำงานของนิวรอนที่มีจำนวนน้อยกว่าก็จะใช้พลังงานน้อยกว่า[64]
รหัสนี้อาจแบ่งได้โดยอีกวิธีหนึ่งเป็น 2 แบบ ก็คือแบบ critically complete (สมบูรณ์อย่างวิกฤติ) หรือ overcomplete (สมบูรณ์เกิน)
- ถ้าจำนวนเวกเตอร์ฐานหลักคือ n เท่ากับ k ซึ่งเป็นมิติของเซตข้อมูลเข้า การเข้ารหัสนี้เรียกว่า สมบูรณ์อย่างวิกฤติ ในกรณีนี้ การเปลี่ยนแปลงเล็ก ๆ น้อย ๆ ของเวกเตอร์ข้อมูลเข้า จะทำให้สัมประสิทธิ์เปลี่ยนโดยฉับพลัน ดังนั้น รหัสจึงไม่สามารถรองรับการการเปลี่ยนสเกล การเลื่อนที่ หรือเสียงรบกวนเล็ก ๆ น้อย ๆ ในข้อมูลขาเข้า
- แต่ถ้าเวกเตอร์ฐานหลักมีจำนวนมากกว่ามิติของเซตข้อมูลเข้า รหัสก็จะจัดว่า สมบูรณ์เกิน และรหัสที่สมบูรณ์เกินจะเปลี่ยนค่าได้อย่างเรียบ ๆ สำหรับเวกเตอร์ข้อมูลเข้าที่มีค่าในระหว่าง ๆ และทนทานต่อเสียงรบกวนได้ดี[66]
เปลือกสมองส่วนการเห็นปฐมภูมิของมนุษย์ประเมินว่า สมบูรณ์เกินโดยแฟกเตอร์ 500 ดังนั้น ข้อมูลขาเข้าที่ 14x14 (196-dimensional space) จะเข้ารหัสโดยนิวรอนประมาณ 100,000 ตัว[64]
หลักฐานทางชีววิทยา[แก้]
การเข้ารหัสโดยน้อยเซลล์ อาจเป็นกลยุทธ์ทั่วไปของระบบประสาทเพื่อเพิ่มความจุของความจำ คือ เพื่อปรับตัวให้เข้ากับสิ่งแวดล้อม สัตว์จะต้องเรียนรู้ว่า สิ่งเร้าเช่นไรสัมพันธ์กับรางวัลหรือการลงโทษ แล้วจำแนกสิ่งเร้าที่เสริมแรงเช่นนี้จากสิ่งเร้าที่คล้ายกันแต่ไม่เกี่ยวกัน ปฏิบัติการเช่นนี้จะต้องมีหน่วยความจำสาระ (associative memory) ที่เฉพาะเจาะจงต่อสิ่งเร้า ที่นิวรอนไม่กี่ตัวจากทั้งกลุ่มจะตอบสนองต่อสิ่งเร้าหนึ่ง ๆ และนิวรอนแต่ละตัว ๆ จะตอบสนองต่อสิ่งเร้าไม่กี่อย่างจากสิ่งเร้าที่เป็นไปได้ทั้งหมด
งานทฤษฎีเรื่อง Sparse distributed memory (ความจำแบบกระจายและมากไปด้วยศูนย์)[67] ได้เสนอว่า การเข้ารหัสโดยน้อยเซลล์จะเพิ่มความจุของความจำสาระ โดยลดความคาบเกี่ยวกันระหว่างการทำงานของนิวรอนที่เป็นตัวแทนลักษณะสิ่งเร้า ส่วนในงานทดลอง การเข้ารหัสโดยน้อยเซลล์ของข้อมูลความรู้สึก ได้พบในระบบรับความรู้สึกหลายอย่างรวมทั้งระบบการเห็น[68] ระบบการได้ยิน[69] ระบบรู้สัมผัส[70] และระบบรู้กลิ่น[71]
อย่างไรก็ดี แม้จะมีหลักฐานเพิ่มขึ้นเรื่อย ๆ เกี่ยวกับการใช้รหัสเช่นนี้อย่างกว้างขวางในระบบประสาท รวมทั้งข้อสนับสนุนทางทฤษฎีเกี่ยวกับความสำคัญของมัน งานที่แสดงว่า รหัสโดยน้อยเซลล์จะเพิ่มความเฉพาะเจาะจงต่อสิ่งเร้าของระบบความจำสาระก็ไม่ค่อยมีจนกระทั่งเร็ว ๆ นี้
ในปี 2557 นักกายวิภาคชาวสวีเดน-อังกฤษ (Gero Miesenböck) ที่มหาวิทยาลัยออกซฟอร์ดได้ทำงานวิเคราะห์กับระบบรู้กลิ่นของแมลงวันทอง[72] ในแมลงวันทอง การเข้ารหัสกลิ่นโดยน้อยเซลล์ของ Kenyon cell ใน Mushroom bodies เชื่อว่า จะเป็นตัวกำหนดตำแหน่งแบบเข้าเลขอย่างแม่นยำจำนวนมากเพื่อบรรจุความจำเกี่ยวกับกลิ่นโดยเฉพาะ ๆ
งานวิจัยอีกงานปี 2557[73] แสดงว่า ความมากน้อยของนิวรอนที่ทำงาน (sparseness) จะควบคุมโดยวงจรป้อนกลับเชิงผกผันระหว่าง Kenyon cells และ GABAergic anterior paired lateral (APL) neuron การจงใจกระตุ้นและหยุดการทำงานอย่างเป็นระบบของส่วนแต่ละส่วนในวงจรนี้แสดงว่า Kenyon cells จะกระตุ้นให้ APL ทำงาน และในทางกลับกัน APL ก็จะยับยั้ง Kenyon cells ไม่ให้ทำงาน การระงับวงจรป้อนกลับ Kenyon cell-APL จะกวนการเข้ารหัสแบบน้อยเซลล์ที่ตอบสนองต่อกลิ่นของ Kenyon cell, เพิ่มสหสัมพันธ์ในระหว่างกลิ่นต่าง ๆ, และกันแมลงวันไม่ให้เรียนรู้แยกแยะกลิ่นที่คล้ายกัน แต่ไม่กันสำหรับกลิ่นที่ต่างกัน ผลเช่นนี้แสดงว่า การยับยั้งแบบป้อนกลับที่ระงับการทำงานของ Kenyon cell ทำให้สามารถดำรงการเข้ารหัสกลิ่นอย่างน้อยเซลล์ แยกแยะไม่ให้ปนกลิ่น และดังนั้น ดำรงความเฉพาะเจาะจงต่อกลิ่นในระบบความจำ
ดูเพิ่ม[แก้]
เชิงอรรถ[แก้]
- ↑ คือปรากฏการณ์ทุติยภูมิที่เป็นผลของปรากฏการณ์ที่เป็นเหตุจริง ๆ
อ้างอิง[แก้]
- ↑ Brown EN, Kass RE, Mitra PP (May 2004). "Multiple neural spike train data analysis: state-of-the-art and future challenges". Nat. Neurosci. 7 (5): 456–61. doi:10.1038/nn1228. PMID 15114358. S2CID 562815.
- ↑ Johnson, K. O. (June 2000). "Neural coding". Neuron. 26 (3): 563–566. doi:10.1016/S0896-6273(00)81193-9. ISSN 0896-6273. PMID 10896153.
- ↑ 3.0 3.1 3.2 Thorpe, S.J. (1990). "Spike arrival times: A highly efficient coding scheme for neural networks". ใน Eckmiller, R.; Hartmann, G.; Hauske, G. (บ.ก.). Parallel processing in neural systems and computers (PDF). North-Holland. pp. 91–94. ISBN 978-0-444-88390-2.
- ↑ Gerstner, Wulfram; Kistler, Werner M. (2002). Spiking Neuron Models: Single Neurons, Populations, Plasticity. Cambridge University Press. ISBN 978-0-521-89079-3.
- ↑ 5.0 5.1 5.2 5.3 Stein RB, Gossen ER, Jones KE (May 2005). "Neuronal variability: noise or part of the signal?". Nat. Rev. Neurosci. 6 (5): 389–97. doi:10.1038/nrn1668. PMID 15861181. S2CID 205500218.
- ↑ Chen, G; Wang, LP; Tsien, JZ (2009). "Neural population-level memory traces in the mouse hippocampus". PLOS ONE. 4 (12): e8256. Bibcode:2009PLoSO...4.8256C. doi:10.1371/journal.pone.0008256. PMC 2788416. PMID 20016843.
- ↑ Zhang, H; Chen, G; Kuang, H; Tsien, JZ (Nov 2013). "Mapping and deciphering neural codes of NMDA receptor-dependent fear memory engrams in the hippocampus". PLOS ONE. 8 (11): e79454. Bibcode:2013PLoSO...879454Z. doi:10.1371/journal.pone.0079454. PMC 3841182. PMID 24302990.
- ↑ "Brain Decoding Project". เก็บจากแหล่งเดิมเมื่อ 2017-10-14. สืบค้นเมื่อ 2018-01-07.
- ↑ "The Simons Collaboration on the Global Brain". Simons Foundation.
- ↑ Burcas, G.T; Albright T.D. (1999). "Gauging sensory representations in the brain" (PDF). Salk Institute for Biological Studies.
{{cite web}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ Gerstner W, Kreiter AK, Markram H, Herz AV (November 1997). "Neural codes: firing rates and beyond". Proc. Natl. Acad. Sci. U.S.A. 94 (24): 12740–1. Bibcode:1997PNAS...9412740G. doi:10.1073/pnas.94.24.12740. PMC 34168. PMID 9398065.
- ↑
Aur, D; Jog, MS (2010). Neuroelectrodynamics: Understanding the brain language. IOS Press. doi:10.3233/978-1-60750-473-3-i.
{{cite book}}: CS1 maint: uses authors parameter (ลิงก์) - ↑
Aur, D; Connolly, CI; Jog, MS (2005). "Computing spike directivity with tetrodes". Journal of Neuroscience Methods. 149 (1): 57–63. doi:10.1016/j.jneumeth.2005.05.006. PMID 15978667.
{{cite journal}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ Aur, D.; Jog, M.S. (2007). "Reading the Neural Code: What do Spikes Mean for Behavior?". Nature Precedings. doi:10.1038/npre.2007.61.1.
- ↑ Fraser, A.; Frey, A. H. (1968). "Electromagnetic emission at micron wavelengths from active nerves". Biophysical Journal. 8 (6): 731–734. doi:10.1016/s0006-3495(68)86517-8. PMC 1367349. PMID 5699805.
- ↑ Aur, D (2012). "A comparative analysis of integrating visual information in local neuronal ensembles". Journal of neuroscience methods. 207 (1): 23–30. doi:10.1016/j.jneumeth.2012.03.008. PMC 3636996. PMID 22480985.
- ↑ Kandel, E.; Schwartz, J.; Jessel, T.M. (1991). Principles of Neural Science (3rd ed.). Elsevier. ISBN 0444015620.
- ↑ Adrian, ED; Zotterman, Y (1926). "The impulses produced by sensory nerve endings: Part II: The response of a single end organ". J Physiol. 61: 151–171. doi:10.1113/jphysiol.1926.sp002281.
{{cite journal}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ 19.0 19.1 Gerstner and Kistler (2002). "1.5 Rate Codes". Spiking Neuron Models. Single Neurons, Populations, Plasticity. Cambridge University Press. เก็บจากแหล่งเดิมเมื่อ 2017-07-06. สืบค้นเมื่อ 2018-01-26.
{{cite web}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ Forrest MD (2014). "Intracellular Calcium Dynamics Permit a Purkinje Neuron Model to Perform Toggle and Gain Computations Upon its Inputs". Frontiers in Computational Neuroscience. 8: 86. doi:10.3389/fncom.2014.00086. PMC 4138505. PMID 25191262.
- ↑ Forrest MD (December 2014). "The sodium-potassium pump is an information processing element in brain computation". Frontiers in Physiology. 5 (472): 472. doi:10.3389/fphys.2014.00472. PMC 4274886. PMID 25566080.
- ↑ Dayan, Peter; Abbott, L. F. (2001). Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Massachusetts Institute of Technology Press. ISBN 978-0-262-04199-7.
- ↑ Butts DA, Weng C, Jin J, และคณะ (September 2007). "Temporal precision in the neural code and the timescales of natural vision". Nature. 449 (7158): 92–5. Bibcode:2007Natur.449...92B. doi:10.1038/nature06105. PMID 17805296. S2CID 4402057.
- ↑ Singh & Levy (2017). "A consensus layer V pyramidal neuron can sustain interpulse-interval coding". PLoS ONE.
{{cite web}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ van Hemmen, J Leo; Sejnowski, TJ (2006). 23 Problems in Systems Neuroscience. Oxford Univ. Press. pp. 143–158.
{{cite book}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ 26.0 26.1 26.2 26.3 Theunissen, F; Miller, JP (1995). "Temporal Encoding in Nervous Systems: A Rigorous Definition". Journal of Computational Neuroscience. 2: 149–162. doi:10.1007/bf00961885.
- ↑ Zador, Stevens, Charles, Anthony. "The enigma of the brain". © Current Biology 1995, Vol 5 No 12. สืบค้นเมื่อ August 4, 2012.
- ↑ Kostal L, Lansky P, Rospars JP (November 2007). "Neuronal coding and spiking randomness". Eur. J. Neurosci. 26 (10): 2693–701. doi:10.1111/j.1460-9568.2007.05880.x. PMID 18001270. S2CID 15367988.
- ↑ Gupta, Nitin; Singh, Swikriti Saran; Stopfer, Mark (2016-12-15). "Oscillatory integration windows in neurons". Nature Communications (ภาษาอังกฤษ). 7: 13808. doi:10.1038/ncomms13808. ISSN 2041-1723. PMID 27976720.
- ↑ Geoffrois, E.; Edeline, J.M.; Vibert, J.F. (1994). "Learning by Delay Modifications". ใน Eeckman, Frank H. (บ.ก.). Computation in Neurons and Neural Systems. Springer. pp. 133–8. ISBN 978-0-7923-9465-5.
- ↑ Sjöström, Jesper; Gerstner, Wulfram. "Spike-timing dependent plasticity". scholarpedia. สืบค้นเมื่อ 2018-01-26.
{{cite web}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ Gollisch, T.; Meister, M. (2008-02-22). "Rapid Neural Coding in the Retina with Relative Spike Latencies". Science. 319 (5866): 1108–1111. doi:10.1126/science.1149639. PMID 18292344.
- ↑ Wainrib, Gilles; Michèle, Thieullen; Khashayar, Pakdaman (2010-04-07). "Intrinsic variability of latency to first-spike". Biological Cybernetics. 103 (1): 43–56. doi:10.1007/s00422-010-0384-8.
- ↑ Victor, Johnathan D (2005). "Spike train metrics". Current Opinion in Neurobiology. 15 (5): 585–592. doi:10.1016/j.conb.2005.08.002.
- ↑ Hallock, Robert M.; Di Lorenzo, Patricia M. (2006). "Temporal coding in the gustatory system". Neuroscience & Biobehavioral Reviews. 30 (8): 1145–1160. doi:10.1016/j.neubiorev.2006.07.005.
- ↑ Carleton, Alan; Accolla, Riccardo; Simon, Sidney A. (2010). "Coding in the mammalian gustatory system". Trends in Neurosciences. 33 (7): 326–334. doi:10.1016/j.tins.2010.04.002.
- ↑ Stevens & Zador 1995, pp. 1371 "There is thus ample evidence that, at least under some circumstances, the timing of spikes cannot be accounted for by a simple frequency code, and that there is potentially useful 'extra' information contained in spike trains. It is much harder to show that this extra information is actually used in the neural code. There are other interpretations for the experimental deviations from the instantaneous frequency hypothesis. They might arise, for example, as by-products of cortical architecture, the results of shared inputs. Alternatively, they might improve the performance of cortical processing, without actually providing an additional information channel."
- ↑ Wilson, Rachel I (2008). "Neural and behavioral mechanisms of olfactory perception". Current Opinion in Neurobiology. 18 (4): 408–412. doi:10.1016/j.conb.2008.08.015.
- ↑ 39.0 39.1 Diesseroth, Karl (2008-11-21). Personal Growth Series: Karl Diesseroth on Cracking the Neural Code (การบรรยาย). Google Tech Talks.
{{cite AV media}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ 40.0 40.1 Han, X; Qian, X; Stern, P; Chuong, AS; Boyden, ES (2009). Informational lesions: optical perturbations of spike timing and neural synchrony via microbial opsin gene fusions. Cambridge, MA: MIT Media Lab.
{{cite book}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ 41.0 41.1 Montemurro, Marcelo A.; Rasch, Malte J.; Murayama, Yusuke; Logothetis, Nikos K.; Panzeri, Stefano (2008). "Phase-of-Firing Coding of Natural Visual Stimuli in Primary Visual Cortex". Current Biology. 18 (5): 375–380. doi:10.1016/j.cub.2008.02.023. PMID 18328702.
- ↑ Fries P, Nikolić D, Singer W (July 2007). "The gamma cycle". Trends Neurosci. 30 (7): 309–16. doi:10.1016/j.tins.2007.05.005. PMID 17555828. S2CID 3070167.
- ↑ 43.0 43.1 43.2 Havenith MN, Yu S, Biederlack J, Chen NH, Singer W, Nikolić D (June 2011). "Synchrony makes neurons fire in sequence, and stimulus properties determine who is ahead". J. Neurosci. 31 (23): 8570–84. doi:10.1523/JNEUROSCI.2817-10.2011. PMC 6623348. PMID 21653861.
- ↑ Thorpe, SJ (1990). "Spike arrival times: A highly efficient coding scheme for neural networks" (PDF). Parallel processing in neural systems. คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2012-02-15. สืบค้นเมื่อ 2018-01-26.
{{cite web}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ Wu S, Amari S, Nakahara H (May 2002). "Population coding and decoding in a neural field: a computational study". Neural Comput. 14 (5): 999–1026. doi:10.1162/089976602753633367. PMID 11972905. S2CID 1122223.
- ↑ Maunsell JH, Van Essen DC (May 1983). "Functional properties of neurons in middle temporal visual area of the macaque monkey. I. Selectivity for stimulus direction, speed, and orientation". J. Neurophysiol. 49 (5): 1127–47. doi:10.1152/jn.1983.49.5.1127. PMID 6864242. S2CID 8708245.
- ↑
Krakauer, John; Ghez, Claude. "Voluntary Movement" (PDF). Principles of Neural Science. p. 766. คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2012-05-11.
{{cite web}}: CS1 maint: uses authors parameter (ลิงก์) - ↑
PMID 3749885 (PMID 3749885)
Citation will be completed automatically in a few minutes. Jump the queue or expand by hand - ↑ Sachs, Murray B.; Young, Eric D. (November 1979). "Representation of steady-state vowels in the temporal aspects of the discharge patterns of populations of auditory-nerve fibers". The Journal of the Acoustical Society of America. 66 (5): 1381–1403. Bibcode:1979ASAJ...66.1381Y. doi:10.1121/1.383532. PMID 500976.
- ↑ Miller, M.I.; Sachs, M.B. (June 1984). "Representation of voice pitch in discharge patterns of auditory-nerve fibers". Hearing Research. 14 (3): 257–279. doi:10.1016/0378-5955(84)90054-6. PMID 6480513. S2CID 4704044.
- ↑ Miller, M.I.; Sachs, M.B. (1983). "Representation of stop consonants in the discharge patterns of auditory-nerve fibrers". The Journal of the Acoustical Society of America. 74 (2): 502–517. Bibcode:1983ASAJ...74..502M. doi:10.1121/1.389816. PMID 6619427.
- ↑ Hubel DH, Wiesel TN (October 1959). "Receptive fields of single neurones in the cat's striate cortex". J. Physiol. 148 (3): 574–91. doi:10.1113/jphysiol.1959.sp006308. PMC 1363130. PMID 14403679.
- ↑ Schneidman, E; Berry, MJ; Segev, R; Bialek, W (2006), "Weak Pairwise Correlations Imply Strongly Correlated Network States in a Neural Population", Nature, Nature 440, 1007-1012, 440: 1007–1012, doi:10.1038/nature04701, PMC 1785327, PMID 16625187
- ↑ Amari, SL (2001), Information Geometry on Hierarchy of Probability Distributions, IEEE Transactions on Information Theory 47, 1701-1711
- ↑ Onken, A; Grünewälder, S; Munk, MHJ; Obermayer, K (2009), "Analyzing Short-Term Noise Dependencies of Spike-Counts in Macaque Prefrontal Cortex Using Copulas and the Flashlight Transformation", PLoS Comput Biol, 5 (11): e1000577, doi:10.1371/journal.pcbi.1000577, PMC 2776173, PMID 19956759
- ↑ Johnson, KO (Jun 1980). "Sensory discrimination: neural processes preceding discrimination decision". J Neurophysiol. 43 (6): 1793–815. doi:10.1152/jn.1980.43.6.1793. PMID 7411183.
- ↑ Panzeri; Schultz; Treves; Rolls (1999). "Correlations and the encoding of information in the nervous system". Proc Biol Sci. 266 (1423): 1001–12. doi:10.1098/rspb.1999.0736. PMC 1689940. PMID 10610508.
- ↑ Merzenich, MM (Jun 1996). "Primary cortical representation of sounds by the coordination of action-potential timing". Nature. 381 (6583): 610–3. Bibcode:1996Natur.381..610D. doi:10.1038/381610a0. PMID 8637597. S2CID 4258853.
- ↑
Dayan, P ; Abbott, LF (2001). Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Cambridge, Massachusetts: The MIT Press.
{{cite book}}: CS1 maint: uses authors parameter (ลิงก์) - ↑
Rieke, F; Warland, D; de Ruyter van Steveninck, R; Bialek, W (1999). Spikes: Exploring the Neural Code. Cambridge, Massachusetts: The MIT Press.
{{cite book}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ Mathis A, Herz AV, Stemmler MB (July 2012). "Resolution of nested neuronal representations can be exponential in the number of neurons". Phys. Rev. Lett. 109 (1): 018103. Bibcode:2012PhRvL.109a8103M. doi:10.1103/PhysRevLett.109.018103. PMID 23031134.
- ↑ Olshausen, Bruno A; Field, David J (1996). "Emergence of simple-cell receptive field properties by learning a sparse code for natural images" (PDF). Nature. 381 (6583): 607–609. doi:10.1038/381607a0. PMID 8637596. คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2015-11-23. สืบค้นเมื่อ 2018-01-26.
- ↑ Gupta, N; Stopfer, M (2014-10-06). "A temporal channel for information in sparse sensory coding". Current Biology. 24 (19): 2247–56. doi:10.1016/j.cub.2014.08.021. PMC 4189991. PMID 25264257.
- ↑ 64.0 64.1 64.2 64.3 Rehn, Martin; Sommer, Friedrich T. (2007). "A network that uses few active neurones to code visual input predicts the diverse shapes of cortical receptive fields" (PDF). Journal of Computational Neuroscience. 22: 135–146. doi:10.1007/s10827-006-0003-9.
- ↑ Lee, Honglak; Battle, Alexis; Raina, Rajat; Ng, Andrew Y. (2006). "Efficient sparse coding algorithms" (PDF). Advances in Neural Information Processing Systems.
- ↑ Olshausen, Bruno A.; Field, David J. (1997). "Sparse Coding with an Overcomplete Basis Set: A Strategy Employed by V1?" (PDF). Vision Research. 37 (23): 3311–3325. doi:10.1016/s0042-6989(97)00169-7. คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2018-02-19. สืบค้นเมื่อ 2018-01-26.
- ↑ Kanerva, Pentti (1988). Sparse distributed memory. MIT press.
{{cite book}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ Vinje, WE; Gallant, JL (2000). "Sparse coding and decorrelation in primary visual cortex during natural vision". Science. 287: 1273–1276. doi:10.1126/science.287.5456.1273. PMID 10678835.
- ↑ Hromádka, T; Deweese, MR; Zador, AM (2008). "Sparse representation of sounds in the unanesthetized auditory cortex". PLoS Biol. 6: e16. doi:10.1371/journal.pbio.0060016. PMC 2214813. PMID 18232737.
- ↑ Crochet, S; Poulet, JFA; Kremer, Y; Petersen, CCH (2011). "Synaptic mechanisms underlying sparse coding of active touch". Neuron. 69: 1160–1175. doi:10.1016/j.neuron.2011.02.022. PMID 21435560.
- ↑ Ito, I; Ong, RCY; Raman, B; Stopfer, M (2008). "Sparse odor representation and olfactory learning". Nat Neurosci. 11: 1177–1184. doi:10.1038/nn.2192. PMC 3124899. PMID 18794840.
- ↑ "A sparse memory is a precise memory". Oxford Science blog. 2014-02-28.
- ↑ Lin, Andrew C.; และคณะ (2014). "Sparse, decorrelated odor coding in the mushroom body enhances learned odor discrimination". Nature Neuroscience. 17 (4): 559–568.
แหล่งข้อมูลอื่น[แก้]
- Foldiak P, Endres D, Sparse coding, Scholarpedia, 3 (1) :2984, 2008.
- Dayan P & Abbott LF. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Cambridge, Massachusetts: The MIT Press; 2001. ISBN 0-262-04199-5
- Rieke F, Warland D, de Ruyter van Steveninck R, Bialek W. Spikes: Exploring the Neural Code. Cambridge, Massachusetts: The MIT Press; 1999. ISBN 0-262-68108-0
- Tsien, JZ.; และคณะ (2014). "On initial Brain Activity Mapping of episodic and semantic memory code in the hippocampus". Neurobiology of Learning and Memory. 105: 200–210. doi:10.1016/j.nlm.2013.06.019.[ลิงก์เสีย]




