อุณหพลศาสตร์
ลิงก์ข้ามภาษาในบทความนี้ มีไว้ให้ผู้อ่านและผู้ร่วมแก้ไขบทความศึกษาเพิ่มเติมโดยสะดวก เนื่องจากวิกิพีเดียภาษาไทยยังไม่มีบทความดังกล่าว กระนั้น ควรรีบสร้างเป็นบทความโดยเร็วที่สุด |

| อุณหพลศาสตร์ |
|---|
 |
อุณหพลศาสตร์ (/อุน-หะ-พะ-ละ-สาด/ หรือ /อุน-หะ-พน-ละ-สาด/) หรือ เทอร์โมไดนามิกส์ (อังกฤษ: thermodynamics; มาจากภาษากรีก thermos = ความร้อน และ dynamis = กำลัง) เป็นสาขาของฟิสิกส์ ที่ศึกษาความสัมพันธ์เกี่ยวกับ ความร้อน อุณหภูมิ งาน และพลังงาน ในช่วงแรกการศึกษาอุณหพลศาสตร์เกิดจากการศึกษาเรื่องเครื่องจักรความร้อน ต่อมาในภายหลัง นักวิทยาศาสตร์ได้ตระหนักว่า อุณหพลศาสตร์ครอบคลุมถึงกระบวนการการเปลี่ยนแปลงมหาศาล ทั้งสิ่งมีชีวิตและสิ่งไม่มีชีวิต ทั้งในโลกตลอดจนทั้งจักรวาล เช่น การทำนายถึงจุดกำเนิดและดับสูญของจักรวาลด้วยกฎข้อที่ 2 ของอุณหพลศาสตร์ และการบ่งบอกทิศทางของเวลา (direction of time) ด้วยการเพิ่มขึ้นของเอนโทรปี อุณหพลศาสตร์เป็นสาขาหลักทางฟิสิกส์นับแต่ช่วงคริสต์ศตวรรษที่ 19 เป็นต้นมา
ประวัติ[แก้]
ของไหลที่เรียกว่าความร้อน ทฤษฎีแคลอริก[แก้]
ความร้อนเป็นความลี้ลับที่นักฟิสิกส์เฝ้าหาคำอธิบายมานานแสนนาน ทฤษฎีที่ใช้อธิบายความร้อนที่นิยมในสมัยก่อนก็คือ ทฤษฎีแคลอริก ที่กล่าวว่าความร้อนเป็นของไหลชนิดหนึ่ง โดยมีส่วนประกอบเป็นสสารที่เรียกว่าแคลอริก ทฤษฎีนี้ถูกเสนอโดย โจเซฟ แบล็ก นักฟิสิกส์ชาวสกอตแลนด์ และอองตวน ลาวัวซิเยร์ นักเคมี ในคริสต์ศตวรรษที่ 18 แบล็กได้นิยามหน่วยความร้อนดังนี้: ความร้อน 1 แคลอรี คือ ความร้อนที่ใช้ในการเพิ่มอุณหภูมิของน้ำ 1 ปอนด์ ขึ้นมา 1 องศาฟาเรนไฮต์ (ในปัจจุบันเราก็ยังใช้หน่วย แคลอรีบ้างเกี่ยวกับเรื่องของโภชนาการ อยู่ เพียงแต่เปลี่ยนนิยามเป็น ความร้อนที่ใช้ในการเพิ่มอุณหภูมิของน้ำ 1 กรัม ขึ้นมา 1 องศาเซลเซียส) งานของเขาได้ถูกนำไปศึกษาต่อในเรื่อง ความร้อนจำเพาะ (specific heat) ของสสารอย่างจริงจังในเวลาต่อมา นอกจากนั้นแบล็กยังได้นิยาม ความร้อนแฝง (latent heat) หรือความร้อนที่ต้องใส่ในระบบเพื่อทำให้วัตถุเปลี่ยนสถานะ เช่น จากของแข็งเป็นของเหลว หรือจากของเหลวเป็นก๊าซ เป็นต้น แบล็กได้สังเกตว่าความร้อนชนิดนี้ไม่ได้ทำให้อุณหภูมิของระบบเพิ่มขึ้นเลย จึงได้ตั้งชื่อว่า ความร้อนแฝง

เครื่องจักรความร้อนและผลงานของการ์โน[แก้]
ในยุคปฏิวัติอุตสาหกรรม เมื่อเราเข้าใจธรรมชาติของความร้อนดีขึ้นจึงมีการประดิษฐ์คิดค้น เครื่องจักรความร้อน มาใช้งานกันอย่างแพร่หลาย ซึ่งนับว่าเครื่องจักรความร้อนเป็นสิ่งที่สำคัญยิ่งในการพัฒนาความรู้ด้านอุณหพลศาสตร์ และต่อมาในปี ค.ศ. 1824 ซาดี การ์โน วิศวกรชาวฝรั่งเศสได้ตีพิมพ์ผลงาน Reflections on the Motive Power of Fire [1] ซึ่งแสดงให้เห็นว่า เมื่อกำหนดแหล่งกำเนิดอุณหภูมิสูงและต่ำคู่ใด ๆ แล้ว เครื่องจักรความร้อนการ์โนเป็นเครื่องจักรที่ให้งานทางกลศาสตร์มากที่สุดเท่าที่เป็นไปได้ (ต่อมาเราทราบว่าเครื่องจักรแบบผันกลับได้ทุกชนิดมีประสิทธิภาพสูงสุดเท่าเครื่องจักรการ์โน) งานของเครื่องจักรการ์โนทำให้เราตระหนักถึงขอบเขตที่ดีที่สุดของเครื่องจักรความร้อนเท่าที่เราทำได้ และยังเป็นผลงานซึ่งทำให้ต่อมาลอร์ด เคลวินและรูด็อล์ฟ เคลาซีอุสค้นพบกฎข้อที่สองของอุณหพลศาสตร์ นักฟิสิกส์หลายท่านถือว่าการ์โนเป็นหนึ่งในผู้ค้นพบกฎข้อที่สองของอุณหพลศาสตร์ อนึ่ง ในสมัยนั้นการ์โนยังเข้าใจผิดว่าความร้อนคือของไหลอยู่ เขาจึงคิดว่าความร้อนทั้งหมดจะไหลจากแหล่งอุณหภูมิสูงไปยังแหล่งอุณหภูมิต่ำทั้งหมด เฉกเช่นน้ำทั้งหมดไหลจากที่สูงไปยังที่ต่ำ ซึ่งเป็นการเข้าใจผิดเนื่องจากต้องมีความร้อนบางส่วนถูกแปรรูปไปเป็นงานที่ผลิตได้จากเครื่องจักรความร้อน (ตามกฎข้อที่ 1 ของอุณหพลศาสตร์) ต่อมา เบอนัว ปอล เอมีล กลาแปรง ได้พยายามเผยแพร่งานของการ์โนโดยสร้างสมการคณิตศาสตร์และไดอะแกรมของเครื่องจักรความร้อนการ์โน ทำให้งานของการ์โนแพร่หลายไปทั่ว
ความร้อนคือการเคลื่อนไหว[แก้]
ในช่วงสงครามประกาศอิสรภาพของอเมริกา ปี ค.ศ. 1798 เบนจามิน ทอมป์สัน (ต่อมาได้รับแต่งตั้งเป็น เคานท์รัมฟอร์ด) สนใจธรรมชาติของความร้อนมาก และรู้สึกไม่พอใจกับทฤษฎีแคลอริกที่ผู้คนยอมรับกันในขณะนั้น ช่วงที่รัมฟอร์ดได้ถูกแต่งตั้งให้ควบคุมหน่วยปืนใหญ่ของกองทัพ เขาได้สังเกตเห็นถึงความร้อนที่เพิ่มขึ้นในปริมาณมหาศาลมากของปืนใหญ่ เขาตั้งข้อสงสัยว่าถ้ามี สสาร ที่ชื่อว่าความร้อนจริง ปืนใหญ่ย่อมสูญเสียสสารเช่นนั้นไปเป็นจำนวนมาก แต่ผลจากการทดลองอย่างระมัดระวังของเขา กลับพบว่าปืนใหญ่มีน้ำหนักเท่าเดิม (หรือสูญเสียไปน้อยมากจนไม่สามารถตรวจสอบได้) รัมฟอร์ดไม่เชื่อว่าจะมีสสารใด ๆ ที่มีมวลน้อยขนาดนั้น เขาจึงได้ตีพิมพ์ในผลงานของเขาใน London Philosophical Transactions ว่า จากการทดลองและการตรวจสอบ อย่างละเอียดถี่ถ้วนของผม ความร้อนไม่สามารถเป็นอื่นใด นอกจากการเคลื่อนที่ (หมายถึงว่า ความร้อนคือพลังงานจลน์นั่นเอง)

กำเนิดกฎข้อที่หนึ่งของอุณหพลศาสตร์[แก้]
ยูลีอุส ฟ็อน ไมเออร์ และเจมส์ จูล เป็นนักวิทยาศาสตร์สองท่านที่นำแนวคิดของรัมฟอร์ดไปศึกษาต่ออย่างจริงจัง โดยในปี ค.ศ. 1840 ฟ็อน ไมเออร์ ผู้เป็นแพทย์และนักวิทยาศาสตร์สมัครเล่น ได้สังเกตถึงความสัมพันธ์ระหว่างความร้อนและงานทางกลศาสตร์ ระหว่างตรวจคนไข้ในเรือ ทำให้ ฟ็อน ไมเออร์ ได้พยายามตีพิมพ์ผลงานเรื่องกฎการอนุรักษ์พลังงาน. อย่างไรก็ตามเนื่องจากความที่ว่าพื้นฐานทางวิทยาศาสตร์ของฟ็อน ไมเออร์ มีน้อย ทำให้ผลงานของเขามีข้อผิดพลาด และถูกปฏิเสธการตีพิมพ์ ในปีถัดมา ฟ็อน ไมเออร์ พยายามส่งผลงานเข้าตีพิมพ์อีกครั้ง โดยถึงแม้จะสำเร็จ แต่ผลงานของเขาถูกมองข้าม เนื่องจากเขาไม่มีชื่อเสียงในฐานะนักฟิสิกส์ ฟ็อน ไมเออร์ ต้องรออีกราว ๆ 20 ปี กว่าจะได้ชื่อเสียงที่เขาสมควรจะได้รับ เมื่อเคลาซีอุสได้พยายามยกย่องเขาแก่สาธารณชนในฐานะผู้คิดค้นกฎข้อที่ 1
กฎการอนุรักษ์พลังงานได้ถูกค้นพบเช่นกันที่อังกฤษ โดยจูลในปี ค.ศ. 1843 จูลเป็นลูกศิษย์ของจอห์น ดอลตัน จึงมีพื้นฐานทางด้านวิทยาศาสตร์อย่างดีเยี่ยม แตกต่างจากฟ็อน ไมเออร์ จูลได้ทดลองเพื่อพิสูจน์ถึงความสัมพันธ์ระหว่างความร้อนและงานทางกลศาสตร์อย่างรัดกุมมาก ทำให้ผลงานของเขาได้รับการยอมรับไปทั่วยุโรป ในปี ค.ศ. 1847 เฮอร์มันน์ ฟอน เฮล์มโฮลทซ์ ได้ตีพิมพ์ผลงานที่นิยามกฎข้อที่ 1 อย่างเป็นทางการใน Über die Erhaltung der Kraft (On the Conservation of Force)
กำเนิดกฎข้อที่สองของอุณหพลศาสตร์[แก้]
ชื่อเทอร์โมไดนามิกส์ ถือกำเนิดขึ้นเป็นครั้งแรกในปี 1849 โดยวิลเลียม ทอมป์สัน หรือลอร์ด เคลวิน นั่นเอง เคลวินประทับใจในงานของจูลเป็นอย่างมาก เคลวินจึงได้คุยและถกกับจูลหลายต่อหลายครั้ง ความสัมพันธ์ของทั้งคู่ดำเนินไปดังนี้ จูลถามปัญหาทอมป์สัน ทอมป์สันวิเคราะห์คำตอบทางทฤษฎี จูลนำบทวิเคราะห์ของทอมป์สันมาทดลอง กลับไปกลับมาเป็นเวลา 4 ปี ในช่วง ปี ค.ศ. 1852 ถึง ค.ศ. 1856 ทำให้ทั้งสองมีผลงานค้นพบร่วมกัน เช่น การแพร่กระจายแบบจูล-ทอมป์สัน (Joule-Thompson expansion) นอกจากนี้จากการศึกษางานของการ์โนอย่างจริงจัง ทำให้เคลวินเริ่มมีแนวคิดเกี่ยวกับกฎข้อที่ 2
ในช่วงเวลาเดียวกันที่ประเทศเยอรมนี (ค.ศ. 1850-ค.ศ. 1860) รูด็อล์ฟ เคลาซีอุส ก็ได้ตีพิมพ์ผลงานที่เกี่ยวข้องกับกฎข้อที่ 2 และทฤษฎีจลน์ของก๊าซมากมาย เช่น ระยะทางอิสระเฉลี่ย (mean free path) หรือ ระยะทางเฉลี่ยที่โมเลกุลจะเคลื่อนที่ได้โดยไม่ชนกับโมเลกุลอื่น ๆ ในปี ค.ศ. 1865 เคลาซีอุสก็ได้นิยาม การเปลี่ยนแปลงของเอนโทรปี (ในมุมมองมหภาค) อย่างเป็นทางการ
ในช่วงเดียวกันนั้น ปีค.ศ. 1854 ฟอน เฮล์มโฮลทซ์ ที่ได้รับแรงบันดาลใจจากงานของจูล เคลวิน และ เคลาซีอุสได้เริ่มตั้งข้อสันนิษฐานเกี่ยวกับจุดดับของจักรวาลว่าจะมีแต่พลังงานเสียในรูปของความร้อนเท่านั้น ไม่มีพลังงานอย่างอื่นอีก เรียกปรากฏการณ์นี้ว่า heat death เนื่องจากข้อสรุปนี้ขัดแย้งกับคำสอนของศาสนาคริสต์และตรงกับความเห็นของเคลวินเป็นอย่างยิ่ง ด้วยความที่เคลวินเป็นผู้เคร่งครัดในคำสอนของศาสนา ทำให้เคลวินรู้สึกกลัดกลุ้มใจในข้อสรุปนี้เป็นอย่างยิ่ง
หลังจากนั้น เคลวินได้นิยามกฎข้อที่ 2 อย่างเป็นทางการในปี ค.ศ. 1874 (ดูนิยามกฎข้อที่ 2 ของเคลวินในหัวข้อถัดไป)
อะตอม ทฤษฎีจลน์ของก๊าซและกลศาสตร์สถิติ[แก้]
ในขณะที่สมมุติฐานเรื่องอะตอมยังไม่เป็นที่ยอมรับกันในสมัยนั้น ด้วยความประทับใจในงานของเคลาซีอุส เจมส์ เคลิร์ก แมกซ์เวลล์ได้พยายามนำสมมุติฐานดังกล่าวมาใช้ และได้สร้างสาขาใหม่ของอุณหพลศาสตร์ขึ้น เรียกว่าทฤษฎีจลน์ของก๊าซ โดยแมกซ์เวลล์ได้อาศัยความรู้เรื่องกลศาสตร์ดั้งเดิมมาคิดกับทุก ๆ อะตอมในระบบ และอาศัยความรู้เรื่องทฤษฎีความน่าจะเป็น ทำให้สามารถสร้างฟังก์ชันความน่าจะเป็นสำหรับความเร็วของแต่ละอะตอมได้สำเร็จ ฟังก์ชันนี้ปัจจุบันเรียกว่า การกระจายตัวแบบแมกซ์เวลล์ ผลการทดลองหลาย ๆ อย่างสนับสนุนทฤษฎีของแมกซ์เวลล์
ที่ออสเตรีย ลูทวิช บ็อลทซ์มัน ประทับใจงานของแมกซ์เวลล์เป็นอย่างมาก และได้นำแนวคิดเรื่องอะตอมและทฤษฎีความน่าจะเป็นไปพัฒนาต่อจนสามารถสร้างนิยามใหม่ของเอนโทรปีในระดับจุลภาคได้ ดังนี้
โดย S แทนเอนโทรปี และ [W] เป็นจำนวนสถานะที่เป็นไปได้ทั้งหมดของอะตอมในระบบ และ k คือ ค่าคงที่บ็อลทซ์มัน ความหมายของสมการของบ็อลทซ์มันก็คือ เอนโทรปีคือค่าที่วัดการกระจายตัวของพลังงานในระบบ ยิ่งพลังงานกระจายตัวกันมาก ทำให้พลังงานไม่มีระเบียบ ไม่เป็นกลุ่มก้อน เราอาจเรียกพลังงานชนิดนี้ว่าพลังงานเสีย โดยพลังงานเสียนี้ไม่สามารถสร้างงานได้ด้วยตนเอง และจะเพิ่มขึ้นเรื่อย ๆ ตามกฎข้อที่ 2 เช่นเดียวกับแมกซ์เวลล์ บ็อลทซ์มันสร้างฟังก์ชัน การกระจายตัวแบบบ็อลทซ์มัน เพื่ออธิบายถึงความน่าจะเป็นของแต่ละสถานะในระบบ อย่างไรก็ตามการค้นพบของบ็อลทซ์มันไม่ได้รับการยอมรับเท่าที่ควร ด้วยความเสียใจ ทำให้บ็อลทซ์มันตัดสินใจจบชีวิตของเขาด้วยมือตัวเองในที่สุด ผลงานของบ็อลทซ์มันในเวลาต่อมาสร้างสาขาใหม่ให้กับฟิสิกส์ นั่นคือ กลศาสตร์สถิติ และ ฟิสิกส์สถิติ
ในปี ค.ศ. 1876 ถึง ค.ศ. 1878 ที่สหรัฐอเมริกา โจซิอาห์ วิลลาร์ด กิ๊บส์ก็ได้ศึกษาเรื่องกลศาสตร์สถิติอย่างจริงจัง และได้ตีพิมพ์ผลงานออกมามากมาย และรวมไว้ในชื่อ On the Equilibrium of Heterogeneous Substances (ว่าด้วยเรื่องดุลยภาพของสสารต่างชนิด) ในผลงานชิ้นนั้นกิ๊บส์ได้นิยาม พลังงานเสรีของกิ๊บส์ ซึ่งเป็นฟังก์ชันที่มีประโยชน์มหาศาลและเป็นที่มาของสาขาใหม่ในเคมีและฟิสิกส์นั่นคือ เคมีฟิสิกส์ (Physical chemistry) และเคมีความร้อน (Thermochemistry) เคยมีเรื่องเล่าว่า ที่อเมริกาไม่มีผู้ใดตระหนักถึงความสามารถของกิ๊บส์ และเมื่ออเมริกาต้องการทำงานวิจัยเรื่องนี้อย่างจริงจัง ทางอเมริกาต้องส่งตัวแทนไปเชิญแมกซ์เวลล์ถึงที่สหราชอาณาจักร โดยแมกซ์เวลล์ได้กล่าวว่า ประเทศคุณนั้นมีเพชรอย่าง วิลลาร์ด กิ๊บส์อยู่แล้ว ไยต้องลำบากมาหาคนอื่นถึงดินแดนห่างไกลอย่างที่นี่อีกเล่า!
ระบบอุณหพลศาสตร์[แก้]
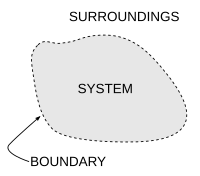
ระบบอุณหพลศาสตร์ (Thermodynamics system) คือส่วนหนึ่งของจักรวาลที่เรากำลังพิจารณาอยู่ โดยเราจะต้องกำหนดขอบเขตของระบบ (ไม่ว่าจะเป็นขอบเขตจริงหรือขอบเขตในจินตนาการ) ให้ชัดเจน ส่วนอื่น ๆ ของจักรวาลที่ไม่อยู่ในระบบเรียกว่า สิ่งแวดล้อม ระบบอุณหพลศาสตร์ที่สำคัญมี 3 ประเภท คือ
- ระบบอิสระ (isolated systems) คือ ระบบที่ปิดกั้นตัวเองจากสิ่งแวดล้อมโดยสมบูรณ์ มวลหรือพลังงานภายนอกไม่สามารถเข้ามาในระบบได้
- ระบบปิด (closed systems) คือ ระบบที่อนุญาตให้พลังงานถ่ายเทผ่านเข้าหรือออกระบบได้ แต่ไม่อนุญาตให้มวลเข้ามาในระบบ (มวลโดยรวมของระบบคงที่ตลอดเวลา) ในการวิเคราะห์กระบวนการทางอุณหพลศาสตร์ เรานิยามพลังงานที่เข้าออกจากระบบให้มีสองประเภทคือ พลังงานความร้อน (พลังงานที่เกิดจากความแตกต่างระหว่างอุณหภูมิของระบบกับอุณหภูมิของสิ่งแวดล้อม) และ พลังงานอื่น (เช่น พลังงานที่เกิดจากงานทางกลศาสตร์)
- ระบบเปิด (open systems) คือ ระบบที่อนุญาตให้ทั้งมวลและพลังงานเข้าออกจากระบบได้ หนังสือบางเล่มกำหนดว่าระบบเปิดจะต้องนิยามให้ปริมาตรคงที่ (fixed volume)
อนึ่ง กฎต่าง ๆ ในอุณหพลศาสตร์จะมีความหมายก็ต่อเมื่อผู้ใช้นิยามระบบอุณหพลศาสตร์อย่างชัดเจนแล้วเท่านั้น เมื่อระบบอยู่ในสภาวะสมดุลในทุก ๆ ด้าน (สมดุลทางกลศาสตร์, สมดุลทางอุณหภูมิ, สมดุลทางเคมี, ฯลฯ) เราจะกล่าวว่า ระบบอยู่ในสถานะที่แน่นอน การวิเคราะห์กระบวนการทางอุณหพลศาสตร์จะวิเคราะห์ได้ก็ต่อเมื่อทุก ๆ ขั้นตอนในกระบวนการสามารถประมาณได้ว่าอยู่ในสภาวะสมดุลเท่านั้น โดยเรียกสภาวะที่พอจะอนุโลมว่าสมดุลได้ว่าสภาวะกึ่งสมดุล (quasi-equilibrium) คุณสมบัติต่าง ๆ ของระบบสามารถอธิบายได้ด้วยสมการของระบบซึ่งระบุถึงความสัมพันธ์ของตัวแปรในระบบ ตัวแปรในระบบอุณหพลศาสตร์ที่สำคัญ คือ ความดัน ปริมาตร อุณหภูมิ พลังงานภายใน เอนโทรปี เอนธาลปี พลังงานเสรีของกิ๊บส์ และพลังงานเสรีของเฮมโฮลทซ์ เป็นต้น
กฎของอุณหพลศาสตร์[แก้]

มีกฎทั้งหมด 4 ข้อในอุณหพลศาสตร์ โดยกฎข้อที่หนึ่งและข้อที่สองนั้น นักวิทยาศาสตร์ทั่วไป ถือว่าเป็นสองทฤษฎีในบรรดาหลักการที่สำคัญที่สุดของฟิสิกส์เลยทีเดียว. อย่างไรก็ตาม กฎบางข้อ เช่น ข้อที่สอง จะเป็นจริงเมื่อเรามองธรรมชาติแบบมหภาคเท่านั้น เมื่อเรามองในระดับจุลภาคหรือระดับอะตอม มีความน่าจะเป็นที่กฎข้อที่สองจะถูกฝ่าฝืน เพียงแต่ความน่าจะเป็นนั้นมีค่าน้อยมาก จนเราไม่สามารถสังเกตเห็นได้ในระดับมหภาคเท่านั้น
ข้อที่ศูนย์[แก้]
กล่าวถึงภาวะสมดุลทางอุณหพลศาสตร์ โดยอธิบายได้ดังนี้
ถ้าระบบ A และ B อยู่ในภาวะสมดุลทางอุณหพลศาสตร์ และระบบ B และ C อยู่ในสภาวะสมดุลทางอุณหพลศาสตร์แล้ว ระบบ A และ C จะอยู่ในภาวะสมดุลทางอุณหพลศาสตร์ด้วยเช่นกัน
นั่นคือภาวะสมดุลทางอุณหพลศาสตร์มีคุณสมบัติถ่ายทอด (transitive) ได้นั่นเอง
ข้อที่หนึ่ง[แก้]
กล่าวถึงกฎทรงพลังงาน โดยอธิบายได้ดังนี้
พลังงานของระบบที่เปลี่ยนแปลงในกระบวนการอะเดียแบติก (กระบวนการที่ไม่มีการถ่ายเทความร้อน) จะไม่ขึ้นกับวิถีทางหรือทิศทางของงานที่กระทำต่อระบบในกระบวนการนั้น ๆ การเปลี่ยนแปลงจะขึ้นอยู่กับสถานะเริ่มต้นและสถานะสุดท้ายเท่านั้น
นั่นคือการเปลี่ยนแปลงพลังงานของระบบมีคุณสมบัติความไม่แปรผัน (invariance) ต่อทิศทางของกระบวนการในกระบวนการอะเดียแบติก. เราสามารถแสดงได้ว่ากฎข้อนี้เขียนแทนได้ด้วยสัญลักษณ์ทางคณิตศาสตร์ โดย E หมายถึงพลังงานของระบบ, Q หมายถึงพลังงานความร้อนที่เข้าสู่ระบบ, และ W หมายถึงงานที่กระทำต่อระบบ.
ข้อที่สอง[แก้]
กล่าวถึงการเพิ่มขึ้นของเอนโทรปีหรือพลังงานเสียในระบบอิสระ โดยอธิบายได้หลายแบบดังนี้
ไม่มีเครื่องจักรความร้อนใด ๆ ที่จะให้ประสิทธิภาพ 100 % (เคลวิน-พลังค์)
ความร้อนจากแหล่งที่มีอุณหภูมิต่ำ ไม่สามารถถ่ายเทไปยังแหล่งที่มีอุณหภูมิสูงกว่าได้ โดยธรรมชาติ (เคลาซีอุส)
เอนโทรปีของระบบอิสระไม่มีทางที่จะลดลงในกระบวนการใดๆ (ทั่วไป)
นั่นคือการเปลี่ยนแปลงเอนโทรปีของระบบมีคุณสมบัติเป็นฟังก์ชันเพิ่มทางเดียว (monotonically increasing) โดยเราพิจารณาเอนโทรปีเป็นฟังก์ชันของเวลา. จากคุณสมบัตินี้ทำให้นักวิทยาศาสตร์เชื่อว่าเราสามารถพิจารณาเอนโทรปีในการระบุทิศทางของเวลาได้
ข้อที่สาม[แก้]
กล่าวถึงอุณหภูมิศูนย์องศาสัมบูรณ์ โดยอธิบายได้ดังนี้
เมื่ออุณหภูมิสัมบูรณ์ลู่เข้าศูนย์ เอนโทรปีของระบบจะลู่เข้าค่าคงที่
สรุปพลังงานในอุณหพลศาสตร์[แก้]
เมื่อพิจารณาจากสมการสมดุลพลังงานในระบบอุณหพลศาสตร์ จะได้ระดับของพลังงานจำนวนหนึ่งที่เรียกชื่อว่า Thermodynamic potential ซึ่งสามารถวัดได้จากระบบ พลังงานที่สำคัญ 5 ตัวได้แก่
| 1. พลังงานภายใน | |
| 2. พลังงานเสรีของเฮล์มโฮลทซ์ | |
| 3. เอนทาลปี | |
| 4. พลังงานเสรีของกิ๊บส์ | |
| 5. Grand potential |
สำหรับพลังงานอื่นๆ ในระบบอุณหพลศาสตร์สามารถหาได้จากการคำนวณโดยใช้สมการของเลอช็องดร์ เพื่อใช้ตรวจสอบการเปลี่ยนแปลงพลังงานภายในระบบนับจากสภาวะเริ่มต้นถึงสภาวะสิ้นสุด พลังงานที่ใช้ไปขึ้นอยู่กับค่าคงที่ของระบบ เช่นค่าของอุณหภูมิหรือความดัน พลังงานภายในหมายถึงพลังงานภายในระบบ เอนทาลปีคือพลังงานภายในระบบบวกกับพลังงานจากงานของแรงดัน-ปริมาตร ส่วนพลังงานของเฮล์มโอลทซ์และพลังงานของกิ๊บส์คือพลังงานที่มีเพียงพอในระบบสำหรับสร้างงาน เมื่ออุณหภูมิกับปริมาตร หรือความดันกับอุณหภูมิมีค่าเท่าเดิมตามลำดับ
อุณหพลศาสตร์สาขาต่างๆ[แก้]
อุณหพลศาสตร์ดั้งเดิม[แก้]
อุณหพลศาสตร์ดั้งเดิม (อังกฤษ: Classical Thermodynamics) คือทฤษฏีแรกๆ ในช่วงต้นคริสต์ศตวรรษ 1800 ที่ให้ความสนใจกับสถานะทางอุณหพลศาสตร์ และคุณสมบัติของพลังงานรูปแบบต่างๆ เช่น พลังงาน งาน และความร้อน ทว่าตามกฎของอุณหพลศาสตร์แล้ว ทฤษฏีทั้งหมดยังไม่สามารถอธิบายในระดับอะตอมได้ อุณหพลศาสตร์ดั้งเดิมพัฒนาขึ้นจากทฤษฏีของ โรเบิร์ต บอยล์ นักเคมี ที่ว่า ความดัน P ของก๊าซปริมาณหนึ่งจะแปรผกผันกับปริมาตร V ของก๊าซนั้นๆ เมื่ออุณหภูมิคงที่ กล่าวอีกนัยหนึ่งคือสมการ PV = k (ค่าคงที่) นั่นเอง จากจุดนี้ทำให้วิทยาศาสตร์ด้านอุณหภูมิเริ่มพัฒนาขึ้นโดยสามารถสร้างเครื่องจักรไอน้ำขึ้นได้เป็นครั้งแรกในอังกฤษโดยโทมัส ซาเวอรี ในปี ค.ศ. 1697 และโทมัส นิวโคเมน ในปี ค.ศ. 1712 กฎข้อที่หนึ่งและสองของอุณหพลศาสตร์ตั้งขึ้นในเวลาต่อมาตามลำดับราวคริสต์ทศวรรษ 1850 โดยอาศัยข้อมูลจากการศึกษาของวิลเลียม แรนคิน, รูด็อล์ฟ เคลาซีอุส และ วิลเลียม ทอมป์สัน (ลอร์ดเคลวิน)
อุณหพลศาสตร์สถิติ[แก้]
อุณหพลศาสตร์แบบดั้งเดิมมีข้อจำกัด ไม่สามารถอธิบายปรากฏการณ์หลายประเภทได้ จำเป็นต้องใช้กลศาสตร์สถิติ หรือ อุณหพลศาสตร์สถิติ (อังกฤษ: Statistical Thermodynamics) มาช่วยอฺธิบาย ตัวอย่างเช่น กฎของอุณหพลศาสตร์อาจใช้อธิบายได้ว่าปฏิกิริยาหนึ่ง ๆ จะเกิดขึ้นได้เอง แต่ไม่ได้อธิบายเกี่ยวกับเวลาที่ใช้ในการทำปฏิกิริยาเอาไว้ ทำให้บางครั้งผลการทดลองได้ผลไม่ตรงตามกฎของอุณหพลศาสตร์ ยกตัวอย่างเช่น ปฏิกิริยารวมตัวระหว่างไฮโดรเจนและออกซิเจนเป็นน้ำ
จากการพิจารณาพลังงานเสรีของน้ำพบว่ามีค่าน้อยกว่าของไฮโดรเจนและออกซิเจน ดังนั้นปฏิกิริยานี้ควรจะเกิดขึ้นได้ แต่จากการทดลองที่อุณหภูมิปกติพบว่าไม่เกิดปฏิกิริยา ในความเป็นจริงปฏิกิริยาดังกล่าวเกิดช้ามาก จนสังเกตไม่ได้ ถ้าเราใส่ตัวเร่งปฏิกิริยาลงไปก็จะได้น้ำตามสมการ
ข้อจำกัดอีกประการหนึ่งก็คือ อุณหพลศาสตร์ไม่สามารถบอกได้ว่า งาน ที่เกิดขึ้นจริงในระบบจะมีค่าเท่าใด บอกได้แต่เพียงว่างานที่เกิดขึ้นได้มากที่สุดจะมีค่าเท่าใด ทั้งนี้เนื่องจากงานที่เกิดขึ้นได้มากสุดเกิดจากกระบวนการผันกลับได้ ในขณะที่กระบวนการที่เกิดขึ้นจริงเป็นกระบวนการผันกลับไม่ได้
อย่างไรก็ตามอุณหพลศาสตร์ดั้งเดิมมีข้อดีตรงที่ ทฤษฎีนี้เป็นอิสระต่อทฤษฎีอะตอม ไม่ว่าทฤษฎีอะตอมจะเปลี่ยนแปลงไปอย่างไรก็ตาม เรายังสามารถใช้อุณหพลศาสตร์ในการอธิบายปรากฏการณ์ธรรมชาติในระดับมหภาคได้เสมอ

อุณหพลศาสตร์เคมี[แก้]
อุณหพลศาสตร์เคมี (อังกฤษ: Chemical Thermodynamics) เป็นการศึกษาความเกี่ยวพันของความร้อนที่เกิดจากปฏิกิริยาทางเคมีหรือจากการเปลี่ยนแปลงสถานะทางฟิสิกส์ภายในขอบเขตของกฎอุณหพลศาสตร์ ในช่วงปี 1873-76 นักคณิตศาสตร์และนักฟิสิกส์ชาวอเมริกันชื่อ โจซิอาห์ วิลลาร์ด กิ๊บส์ ได้เผยแพร่งานวิจัยสามฉบับ ฉบับที่โด่งดังที่สุดคือ On the Equilibrium of Heterogeneous Substances ซึ่งเขาได้แสดงให้เห็นว่ากระบวนการทางอุณหพลศาสตร์สามารถนำมาวิเคราะห์ให้เห็นเป็นภาพได้ จากการศึกษาพลังงาน เอนโทรปี ปริมาตร อุณหภูมิ และความดันของระบบอุณหพลศาสตร์นั้น ทำให้สามารถอธิบายลำดับการเกิดของกระบวนการได้[2] ตลอดช่วงต้นคริสต์ศตวรรษที่ 20 นักเคมีหลายคนเช่น กิลเบิร์ต เอ็น. ลิวอิส, เมิร์ล รันดัล และ อี. เอ. กุกเกินเฮม เริ่มนำสมการคณิตศาสตร์ของกิ๊บส์ไปใช้ในการวิเคราะห์กระบวนการทางเคมีในงานของพวกเขา[3]
ดูเพิ่ม[แก้]
อ้างอิง[แก้]
- ↑ "Reflections on the Motive Power of Fire" (PDF). คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2005-10-02. สืบค้นเมื่อ 2005-09-28.
- ↑ วิลลาร์ด กิ๊บส์ (1993). The Scientific Papers of J. Willard Gibbs, Volume One: Thermodynamics. สำนักพิมพ์ออกซ์โบว. ISBN 0-918024-77-3. OCLC 27974820.
- ↑ กิลเบิร์ต เอ็น. ลิวอิส; เมิร์ล รันดัล (1923). Thermodynamics and the Free Energy of Chemical Substances. McGraw-Hill Book Co. Inc.
- Malcolm Longair. Theoretical Concepts in Physics : An Alternative View of Theoretical Reasoning in Physics, 2nd edition. Cambridge University Press, 2003. (รายละเอียดของกฎทั้ง 4 ข้อ และ เรื่องของการ์โน และจูล)
- Ronald Lane Reese. University Physics. Brooks Cole, 1999. (รายละเอียดของกฎทั้ง 4 ข้อ)
- George Gamow. Biography of Physics. Harper & brothers, 1961. (see also Dover edition, 1988) (เรื่องของ แบล็ก รัมฟอร์ด และการ์โน)
- Alan Lightman. Great Ideas in Physics. McGraw-Hill, 1992. (เรื่องของฟ็อน ไมเออร์ และ การ์โน )
- Thomas Crump. A Brief History of Science: As Seen Through the Development of Scientific Instruments. Carroll & Graf Publishers, 2002. (เรื่องของเคลวิน)
- Charles Ruhla. The Physics of Chance: from Blaise Pascal to Niels Bohr. Oxford University Press, 1992. (เรื่องของแมกซ์เวลล์ บ็อลทซ์มัน)
- Cathy Cobb, Harold Goldwhite. Creations of Fire: Chemistry's Lively History from Alchemy to the Atomic Age. Plenum Pr, 1995. (เรื่องราวของกิ๊บส์)
- รศ. เทพจำนงค์ แสงสุนทร. เอกสารประกอบการสอน: กฎข้อที่หนึ่งของอุณหพลศาสตร์. 2005. (อุณหพลศาสตร์ vs. กลศาสตร์สถิติ)
แหล่งข้อมูลอื่น[แก้]
- เว็บไซต์สำหรับศึกษาเกี่ยวกับอุณหพลศาสตร์ เก็บถาวร 2015-06-14 ที่ เวย์แบ็กแมชชีน
- "อุณหพลศาสตร์" ที่ ScienceWorld.com
- ประวัติศาสตร์ของอุณหพลศาสตร์





![{\displaystyle S=k*log[W]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76cb18b6755944dc9a7387c3d02defc648a20c2a)






