คลื่น
ลิงก์ข้ามภาษาในบทความนี้ มีไว้ให้ผู้อ่านและผู้ร่วมแก้ไขบทความศึกษาเพิ่มเติมโดยสะดวก เนื่องจากวิกิพีเดียภาษาไทยยังไม่มีบทความดังกล่าว กระนั้น ควรรีบสร้างเป็นบทความโดยเร็วที่สุด |
บทความนี้อาจขยายความได้โดยการแปลบทความที่ตรงกันในภาษาอังกฤษ คลิกที่ [ขยาย] เพื่อศึกษาแนวทางการแปล
|


คลื่น หมายถึง ลักษณะของการถูกรบกวน ที่มีการแผ่กระจาย เคลื่อนที่ออกไป ในลักษณะของการกวัดแกว่ง หรือกระเพื่อม และมักจะมีการส่งถ่ายพลังงานไปด้วย คลื่นเชิงกลซึ่งเกิดขึ้นในตัวกลาง (ซึ่งเมื่อมีการปรับเปลี่ยนรูป จะมีความแรงยืดหยุ่นในการดีดตัวกลับ) จะเดินทางและส่งผ่านพลังงานจากจุดหนึ่งไปยังอีกจุดหนึ่งในตัวกลาง โดยไม่ทำให้เกิดการเคลื่อนตำแหน่งอย่างถาวรของอนุภาคตัวกลาง คือไม่มีการส่งถ่ายอนุภาคนั่นเอง แต่จะมีการแกว่งกวัด (oscillation) ไปกลับของอนุภาค อย่างไรก็ตามสำหรับ การแผ่รังสีคลื่นแม่เหล็กไฟฟ้า และ การแผ่รังสีแรงดึงดูด นั้นสามารถเดินทางในสุญญากาศได้ โดยไม่ต้องมีตัวกลาง ลักษณะของคลื่นนั้น จะระบุจาก สันคลื่น หรือ ยอดคลื่น (ส่วนที่มีค่าสูงขึ้น) และ ท้องคลื่น (ส่วนที่มีค่าต่ำลง) ในลักษณะ ตั้งฉากกับทิศทางเดินคลื่น เรียก "คลื่นตามขวาง" (transverse wave) หรือ ขนานกับทิศทางเดินคลื่น เรียก "คลื่นตามยาว" (longitudinal wave)
ชนิดของคลื่น[แก้]
1.1 การจำแนกคลื่นตามลักษณะของตัวกลาง แบ่งออกเป็น 2 ประเภท ดังนี้
1) คลื่นกล (mechanical wave) คือ คลื่นที่ต้องอาศัยตัวกลางในการเคลื่อนที่สามารถถ่ายทอดและโมเมนตัมโดยอาศัยความยืดหยุ่นของตัวกลาง เช่น คลื่นเสียง คลื่นน้ำ คลื่นในเส้นเชือก
2) คลื่นแม่เหล็กไฟฟ้า (electromagnetic wave) คือ คลื่นที่ไม่ต้องอาศัยตัวกลางในการเคลื่อนที่ เช่น แสง คลื่นวิทยุ คลื่นโทรทัศน์
1.2 การจำแนกคลื่นตามลักษณะการกำเนิดคลื่น แบ่งเป็น 2 ประเภท ดังนี้
1) คลื่นดล (pulse wave) คือ คลื่นที่เกิดจากแหล่งกำเนิดสั่นเพียงครั้งเดียว ทำให้เกิดคลื่นเพียงหนึ่งลูก อาจมีลักษณะกระจายออกจากแหล่งกำเนิดที่ทำให้เกิดคลื่น เช่น การโยนหินลงไปในน้ำ
2) คลื่นต่อเนื่อง (continuous wave) คือ คลื่นที่เกิดจากการสั่นของแหล่งกำเนิดหลายครั้งติดต่อกัน ทำให้เกิด คลื่นหลายลูกติดต่อกัน โดยความถี่ของคลื่นที่เกิดขึ้นเท่ากับความถี่ของการรบกวนของแหล่งกำเนิดคลื่น เช่น คลื่นน้ำที่ เกิดจากการใช้มอเตอร์
1.3 การจำแนกคลื่นตามลักษณะการเคลื่อนที่แบ่งออกเป็น 2 ประเภท คือ
1) คลื่นตามขวาง (transverse wave) เป็นคลื่นที่ส่งผ่านไปในตัวกลางแล้วทำให้อนุภาค ในตัวกลางเคลื่อนที่ตั้งฉากกับทิศทาง การเคลื่อนที่ของคลื่น เช่น คลื่นตามขวางในเส้นเชือก คลื่นแสง
2) คลื่นตามยาว (longitudinal wave) เป็นคลื่นที่ส่งผ่านไปในตัวกลางแล้วทำให้อนุภาคในตัวกลางเคลื่อนที่ตามแนวขนานกับ ทิศการเคลื่อนที่ของคลื่น เช่น คลื่นเสียง คลื่นสปริง
ส่วนประกอบของคลื่น[แก้]
- สันคลื่น คือ ตำแหน่งที่สูงที่สุดของทุก ๆ คลื่น
- ท้องคลื่น คือ ตำแหน่งต่ำสุดของคลื่น
- แอมพลิจูด คือ ระยะขจัดสูงสุดของคลื่นวัดจากตำแหน่งสมดุล
- คาบ (period) คือ ช่วงเวลาในการสั่น 1 รอบของอนุภาค มีหน่วยเป็นวินาที แทนด้วย T
- ความถี่ (frequency) คือ จำนวนรอบที่อนุภาคสั่นใน 1 วินาที มีหน่วยเป็นรอบต่อวินาที หรือ เฮิร์ท (Hertz) โดยที่คาบและความถี่ มีความสัมพันธ์
- ความยาวคลื่น (wavelength) คือ ระยะทางที่คลื่นไปได้ในช่วงเวลาของ 1 คาบ แทนด้วย บางทีความยาวคลื่น คือ ระยะจากระหว่างจุด 2 จุดที่อยู่ถัดกัน ซึ่งมีลักษณะเหมือนกัน
- ความกว้างคลื่น (bandwidth) คือ ขนาดทางที่คลื่นไปได้ในช่วงเวลาของ 1 วง แทนด้วย บางทีความกว้างคลื่น คือ ขนาดจากระหว่างวง 2 วงที่อยู่ถัดกัน ซึ่งมีลักษณะเหมือนกัน
- อัตราเร็วคลื่นหรืออัตราเร็วเฟสคือ ระยะทางที่คลื่นเคลื่อนที่ได้ 1 ความยาวคลื่น ในเวลา 1 คาบ มีหน่วยเป็นเมตรต่อวินาที (m/s) โดยสำหรับในตัวกลางชนิดเดียวกัน อัตราเร็วคลื่นจะมีค่าคงที่ โดยความยาวคลื่นจะผกผันกับความถี่ นั้นคือ ถ้าความถี่สูง ความยาวคลื่นจะสั้น ส่วนคลื่นที่มีความถี่ต่ำ ความยาวคลื่นจะยาวขึ้น
ตัวกลางของคลื่น[แก้]
ตัวกลางที่คลื่นใช้ในการแผ่กระจายออก แบ่งออกเป็นประเภทได้ตามคุณลักษณะต่อไปนี้:
- ตัวกลางเชิงเส้น มีคุณสมบัติที่ขนาดของผลรวมคลื่น ที่จุดใด ๆ ในตัวกลางมีขนาดเท่ากับผลบวกของขนาดของคลื่นต่างขบวนกัน
- ตัวกลางจำกัด คือ ตัวกลางที่มีขนาดจำกัด
- ตัวกลางเนื้อเดียว คือ ตัวกลางที่มีคุณสมบัติเหมือนๆ กันในทุกตำแหน่ง
- ตัวกลางไอโซทรอปิก คือ ตัวกลางที่มีคุณสมบัติ ไม่ขึ้นกับทิศทาง
สมบัติของคลื่น[แก้]
คลื่นทุกประเภทจะมีพฤติกรรมร่วมที่เหมือนกันภายใต้สภาวะปกติ โดยมีสมบัติดังต่อไปนี้ คือ
- การสะท้อน (en:reflection) คลื่นเปลี่ยนทิศทางโดยการสะท้อนเมื่อตกกระทบพื้นผิว
- การหักเห (en:refraction) คลื่นเปลี่ยนทิศทางเมื่อเคลื่อนที่จากตัวกลางหนึ่งไปยังอีกตัวกลางหนึ่ง
- การเลี้ยวเบน (en:diffraction) คลื่นเคลื่อนที่ขยายวงออกเรื่อยๆ เช่น ลำคลื่นที่วิ่งผ่านออกจากช่องแคบๆ จะมีลักษณะขยายขนาดลำออก
- การแทรกสอด (en:interference) เกิดจากการซ้อนทับกันของคลื่น เมื่อวิ่งมาตัดกัน
- การกระจาย (en:dispersion) องค์ประกอบที่ความถี่ต่างกันของคลื่น จะมีการแยกตัวออกห่างจากกัน
- การแผ่เชิงเส้นตรง (en:rectilinear propagation) การเคลื่อนที่ของคลื่นเป็นเส้นตรง
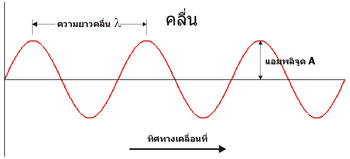
ลักษณะทางกายภาพของคลื่น[แก้]
|

|
ค่าที่ใช้ในการระบุรูปร่างของคลื่น คือ ความถี่ ความยาวคลื่น แอมพลิจูด คาบ
แอมพลิจูด นั้นวัดจากขนาด ของการรบกวนตัวกลาง ที่มากที่สุด ในช่วงหนึ่งคาบ โดยมีหน่วยของการวัดขึ้นกับประเภทของคลื่น เช่น คลื่นในเส้นเชือกมีหน่วยการวัดเป็นระยะทาง (เช่น เมตร) ส่วนคลื่นเสียงมีหน่วยการวัดเป็นความดัน (เช่น ปาสกาล) และ คลื่นเม่เหล็กไฟฟ้า มีหน่วยการวัดเป็น ค่าตามขนาดสนามไฟฟ้า (โวลต์/เมตร) ค่าแอมพลิจูดนั้นอาจมีค่าเป็นคงที่ (เรียกคลื่นประเภทนี้ว่า คลื่นต่อเนื่อง (continuous wave) ย่อ c.w. หรือ อาจมีค่าเปลี่ยนแปลงตามเวลา และ ตำแหน่ง (หากคลื่นเคลื่อนที่ไปในทิศทาง ) การเปลี่ยนแปลงของแอมพลิจูด เรียกว่า ซอง (envelope) ของคลื่น
คาบ เป็นช่วงเวลาที่คลื่นใช้ในการวนครบรอบในการกวัดแกว่ง ความถี่ คือ จำนวนรอบที่คลื่นกวัดแกว่งครบรอบ ในหนึ่งหน่วยเวลา (เช่น ใน 1 วินาที) และมีหน่วยของการวัดเป็น เฮิรตซ์ โดยมีความสัมพันธ์
บางครั้งสมการทางคณิตศาสตร์ของคลื่นอาจอยู่ในรูปของ ความถี่เชิงมุม (en:angular frequency) นิยมใช้สัญลักษณ์ และมีหน่วนเป็น เรเดียนต่อวินาที และมีความสัมพันธ์กับ ดังต่อไปนี้
การเคลื่อนที่ของคลื่น[แก้]

คลื่นที่ไม่เคลื่อนที่เรียก คลื่นนิ่ง (standing wave) เช่น การสั่นของสายไวโอลิน ส่วนคลื่นที่มีการเคลื่อนย้ายตำแหน่งเรียก คลื่นเคลื่อนที่ (travelling wave) การรบกวนในตัวกลางนั้นจะมีการเปลี่ยนแปลงตามเวลา และ ระยะทาง (กรณีทิศทางการเคลื่อนที่ของคลื่น คือ ) อยู่ในรูปทางคณิตศาสตร์ คือ
โดย คือ ซองแอมพลิจูดของคลื่น คือ เลขคลื่น (wave number) คือ เฟส และ คือ ความเร็วของคลื่น
โดย คือ ความยาวคลื่น
สมการคลื่น[แก้]
สมการคลื่นเป็นสมการเชิงอนุพันธ์ย่อย ใช้จำลองพฤติกรรมของคลื่นฮาร์มอนิกเคลื่อนที่ในตัวกลาง สมการคลื่นมีหลายรูปแบบขึ้นกับลักษณะการส่งผ่านของคลื่น และ คุณสมบัติของตัวกลาง ตัวคลื่นก็มีรูปร่างหลากหลาย ไม่จำเป็นจะต้องเป็นคลื่นรูปไซน์เสมอไป
สมการคลื่นในรูปทั่วไป คือ
- และ ใน 1 มิติตามแนวแกน x คือ
และ คำตอบในรูปทั่วไป (กรณี 1 มิติ ในแนวแกน x) ซึ่งค้นพบโดยดาเลมแบร์ คือ
ใช้หมายถึงรูปร่างของคลื่น 2 ลูก โดยที่ เคลื่อนที่ไปในทิศทาง +x และ เคลื่อนที่ไปในทิศทาง -x
นอกจากสมการคลื่น ดังกล่าวข้างต้นแล้ว ยังมีสมการคลื่นชนิดอื่นๆ รวมถึงสมการไม่เป็นเชิงเส้น ซึ่งอาจทำให้เกิดการเคลื่อนมวลสารได้ด้วย เช่น สมการเชรอดิงเงอร์ (en:Schrödinger equation) ซึ่งใช้ในการจำลองพฤติกรรมเชิงคลื่นของอนุภาคในกลศาสตร์ควอนตัม โดยมีคำตอบของสมการเป็นฟังก์ชันคลื่น ที่บ่งบอกถึงความน่าจะเป็นของอนุภาค
ตัวอย่างของคลื่น[แก้]

- คลื่นเชิงกล
- คลื่นทะเล (en:ocean surface wave) หรือ คลื่นผิวทะเล
- เสียง
- คลื่นบนสายเครื่องดนตรี (en:vibrating string)
- คลื่นแม่เหล็กไฟฟ้า
- แสงที่สามารถมองเห็นได้ด้วยตาเปล่า
- คลื่นวิทยุ
- รังสีเอกซ์
- รังสีแกมมา
- รังสีอัลตราไวโอเลต หรือรังสีเหนือม่วง
- รังสีอินฟราเรด หรือรังสีใต้แดง
- คลื่นสนามแรงโน้มถ่วง (en:gravitational wave) (ต่างจากคลื่นจากแรงโน้มถ่วง (en:gravity wave) ซึ่งเป็นคลื่นในของไหล)
อ้างอิง[แก้]
- คลื่น เก็บถาวร 2008-12-05 ที่ เวย์แบ็กแมชชีน คณะวิทยาศาสตร์ มหาวิทยาลัยราชมงคล
- ปรากฏการณ์คลื่น เก็บถาวร 2008-10-25 ที่ เวย์แบ็กแมชชีน
- www.rsu.ac.th/science/physics/pom/physics_2/wave/wave_1.htm
- หนังสือเรียนสาระการเรียนรู้พื้นฐานกลุ่มสาระวิทยาศาสตร์ : ฟิสิกส์ ม.4-6 ช่วงชั้นที่ 4 กรุงเทพ ฯ : อักษรเจริญทัศน์ 2549 หน้าที่ 154-156






















