ทฤษฎีสัมพัทธภาพพิเศษ
บทความนี้ไม่มีการอ้างอิงจากแหล่งที่มาใด |
ทฤษฎีสัมพัทธภาพพิเศษ (อังกฤษ: special relativity) ถูกเสนอขึ้นในปี ค.ศ. 1905 โดยอัลเบิร์ต ไอน์สไตน์ ในบทความของเขา "เกี่ยวกับพลศาสตร์ไฟฟ้าของวัตถุซึ่งเคลื่อนที่ (On the Electrodynamics of Moving Bodies)" สามศตวรรษก่อนหน้านั้น หลักสัมพัทธภาพของกาลิเลโอกล่าวไว้ว่า การเคลื่อนที่ด้วยความเร็วคงที่ทั้งหมดเป็นการสัมพัทธ์ และไม่มีสถานะของการหยุดนิ่งสัมบูรณ์และนิยามได้ คนที่อยู่บนดาดฟ้าเรือคิดว่าตนอยู่นิ่ง แต่คนที่สังเกตบนชายฝั่งกลับบอกว่า ชายบนเรือกำลังเคลื่อนที่ ทฤษฎีของไอน์สไตน์รวมหลักสัมพัทธภาพของกาลิเลโอเข้ากับสมมติฐานที่ว่า ผู้สังเกตทุกคนจะวัดอัตราเร็วของแสงได้เท่ากันเสมอ ไม่ว่าสภาวะการเคลื่อนที่เชิงเส้นด้วยความเร็วคงที่ของพวกเขาจะเป็นอย่างไร
ทฤษฎีนี้มีข้อสรุปอันน่าประหลาดใจหลายอย่างซึ่งขัดกับสามัญสำนึก แต่สามารถพิสูจน์ได้ด้วยการทดลอง ทฤษฎีสัมพัทธภาพพิเศษล้มล้างแนวคิดของปริภูมิสัมบูรณ์และเวลาสัมบูรณ์ของนิวตันโดยการยืนยันว่า ระยะทางและเวลาขึ้นอยู่กับผู้สังเกต และรับรู้เวลากับปริภูมิต่างกันขึ้นอยู่กับผู้สังเกต มันนำมาซึ่งหลักการสมมูลของสสารและพลังงาน ซึ่งสามารถแสดงเป็นสมการชื่อดัง E=mc2 เมื่อ c คืออัตราเร็วของแสง ทฤษฎีสัมพัทธภาพพิเศษสอดคล้องกับกลศาสตร์นิวตันในสำนึกทั่วไปและในการทดลองเมื่อความเร็วของสิ่งต่าง ๆ น้อยมากเมื่อเทียบกับอัตราเร็วแสง
ทฤษฎีนี้เรียกว่า "พิเศษ" เนื่องจากมันประยุกต์หลักสัมพัทธภาพกับกรอบอ้างอิงเฉื่อยเท่านั้น ไอน์สไตน์พัฒนาทฤษฎีสัมพัทธภาพทั่วไปโดยประยุกต์หลักสัมพัทธภาพให้ใช้ทั่วไป กล่าวคือ ใช้ได้กับทุกกรอบอ้างอิง และทฤษฎีดังกล่าวยังรวมผลของความโน้มถ่วง ทฤษฎีสัมพัทธภาพพิเศษไม่ได้รวมผลของความโน้มถ่วง แต่มันสามารถจัดการกับความเร่งได้
ถึงแม้ว่าทฤษฎีสัมพัทธภาพจะทำให้เกิดการสัมพัทธ์กันของปริมาณบางอย่าง เช่น เวลาซึ่งเรามักคิดว่าเป็นปริมาณสัมบูรณ์เนื่องจากประสบการณ์ในชีวิตประจำวัน ถึงกระนั้นมันก็มีปริมาณบางอย่างที่เป็นปริมาณสัมบูรณ์ทั้ง ๆ ที่เราคิดว่ามันน่าจะเป็นปริมาณสัมพัทธ์ กล่าวให้ชัดคือว่า อัตราเร็วของแสงจะเท่ากันสำหรับทุกผู้สังเกต แม้ว่าพวกเขาจะเคลื่อนที่สัมพัทธ์กันก็ตาม ทฤษฎีสัมพัทธภาพแสดงให้เห็นว่า c ไม่ใช่แค่ความเร็วของปรากฏการณ์ที่เรียกว่า แสง เท่านั้น แต่ยังเป็นค่าพื้นฐานที่เชื่อมปริภูมิกับเวลาเข้าด้วยกัน กล่าวโดยเจาะจงคือว่า ทฤษฎีสัมพัทธภาพยืนยันว่าไม่มีวัตถุใดเคลื่อนที่เร็วเท่ากับแสงได้
สมมติฐาน[แก้]
บทความหลัก: สมมติฐานของทฤษฎีสัมพัทธภาพพิเศษ (Einstein Postulate)
- สมมติฐานข้อแรก - หลักสัมพัทธภาพอย่างพิเศษ - กฎทางฟิสิกส์ย่อมเหมือนกันในทุกกรอบอ้างอิงเฉื่อย กล่าวอีกนัยหนึ่งคือ ไม่มีกรอบอ้างอิงพิเศษใด ๆ
- สมมติฐานข้อที่สอง - ความไม่แปรเปลี่ยนของ c - อัตราเร็วของแสงในสุญญากาศเป็นค่าคงที่สากล (c) ซึ่งไม่ขึ้นอยู่กับการเคลื่อนที่ของแหล่งกำเนิดแสงนั้น
พลังของทฤษฎีไอน์สไตน์เกิดขึ้นจากวิธีที่เขาได้มาซึ่งผลลัพธ์อันน่าตื่นตระหนกและดูจะไม่น่าถูกต้องจากข้อสมมุติง่าย ๆ สองอย่างซึ่งค้นพบจากการสังเกต ผู้สังเกตพยายามวัดอัตราเร็วของแสงที่แผ่ออกมา พบว่าได้คำตอบเท่าเดิมไม่ว่าผู้สังเกตหรือองค์ประกอบของระบบวัดจะเคลื่อนที่อย่างไร
ความบกพร่องของกรอบอ้างอิงสัมบูรณ์[แก้]
หลักสัมพัทธภาพ ซึ่งกล่าวว่าไม่มีกรอบอ้างอิงที่อยู่กับที่ นั้นสืบเนื่องมาจากกาลิเลโอ และถูกรวมเข้ากับฟิสิกส์ของนิวตัน อย่างไรก็ตาม ในช่วงปลายศตวรรษที่ 19 การมีอยู่ของคลื่นแม่เหล็กไฟฟ้าทำให้นักฟิสิกส์เสนอแนวคิดว่า เอกภพเต็มไปด้วยสารที่รู้จักในนาม "อีเทอร์" ซึ่งทำตัวเป็นตัวกลางยามที่การสั่นของคลื่นเคลื่อนไป อีเทอร์ถูกตั้งขึ้นเพื่อการมีกรอบอ้างอิงสัมบูรณ์ต้านกับหลักที่ว่าอัตราเร็วของกรอบอ้างอิงใด ๆ สามารถวัดได้ กล่าวอีกอย่างคือ อีเทอร์เป็นสิ่งเดียวที่ถูกตรึงหรือไม่เคลื่อนที่ในเอกภพ อีเทอร์ถูกสมมุติให้มีคุณสมบัติอันอัศจรรย์: มันยืดหยุ่นพอที่จะรองรับคลื่นแม่เหล็กไฟฟ้า และคลื่นนั้นต้องสามารถมีการกระทำกับสสาร ในขณะที่ตัวอีเทอร์เองต้องไม่มีความต้านทานในการเคลื่อนที่สำหรับวัตถุที่ทะลุผ่านมันไป ผลการทดลองต่าง ๆ รวมทั้งการทดลองของไมเคิลสันและเมอร์เลย์ ชี้ให้เห็นว่าโลก 'อยู่กับที่' -- ซึ่งเป็นอะไรที่ยากจะอธิบายได้ เพราะโลกอยู่ในวงโคจรรอบดวงอาทิตย์ ผลลัพธ์อันสละสลวยของไอน์สไตน์ล้มล้างแนวคิดเรื่องอีเทอร์และการอยู่นิ่งสัมบูรณ์ ทฤษฎีสัมพัทธภาพพิเศษถูกเขียนขึ้นไม่ใช่แค่ถือว่ากรอบอ้างอิงเฉพาะใด ๆ นั้นพิเศษ แต่ว่าในสัมพัทธภาพ กรอบหนึ่ง ๆ ต้องสังเกตพบกฎทางฟิสิกส์แบบเดียวกันโดยไม่ขึ้นอยู่กับความเร็วของผู้สังเกต กล่าวให้ชัดคือ อัตราเร็วของแสงในสุญญากาศต้องวัดได้ c เสมอ แม้ว่าจะวัดโดยระบบต่าง ๆ ซึ่งเคลื่อนที่ด้วยความเร็วต่าง ๆ (แต่คงที่)
ผลสรุป[แก้]
บทความหลัก: ผลสรุปของทฤษฎีสัมพัทธภาพพิเศษ
ไอน์สไตน์ได้กล่าวไว้ว่าผลที่ตามมาของทฤษฎีสัมพัทธภาพพิเศษสามารถหาได้จากการพิจารณาการแปลงแบบลอเรนซ์ การแปลงเหล่านี้ รวมทั้งทฤษฎีสัมพัทธภาพพิเศษ นำไปสู่การทำนายลักษณะกายภาพที่ต่างไปจากกลศาสตร์นิวตันเมื่อความเร็วสัมพัทธ์มีค่าเทียบเคียงอัตราเร็วแสง อัตราเร็วแสงนั้นมากกว่าทุกสิ่งที่มนุษย์เคยประสบ จนทำให้ผลบางอย่างซึ่งทำนายจากหลักการสัมพัทธ์นั้นจะขัดกับสัญชาตญาณตั้งแต่แรก:
- การยืดออกของเวลา - เวลาที่ล่วงไประหว่างเหตุการณ์สองอย่างนั้นไม่แปรเปลี่ยนจากผู้สังเกตหนึ่งไปยังผู้สังเกตหนึ่ง แต่มันขึ้นอยู่กับความเร็วสัมพัทธ์ของกรอบอ้างอิงของผู้สังเกต (ตัวอย่างเช่น ปัญหา twin paradox ซึ่งพูดถึงฝาแฝดซึ่งคนหนึ่งบินไปกับยานอวกาศซึ่งเคลื่อนที่ไปด้วยความเร็วใกล้แสง แล้วกลับมาพบว่าแฝดของเขาที่อยู่บนโลกมีอายุมากกว่า)
- สัมพัทธภาพของความพร้อมกัน - เหตุการณ์สองอย่างเกิดขึ้นในที่ที่ต่างกันสองแห่งอย่างพร้อมกันสำหรับผู้สังเกตหนึ่ง อาจไม่พร้อมกันสำหรับผู้สังเกตคนอื่น (ความบกพร่องของความพร้อมกันสัมบูรณ์)
- การหดสั้นเชิงลอเรนซ์ - มิติ (เช่น ความยาว) ของวัตถุเมื่อวัดโดยผู้สังเกตคนหนึ่งอาจเล็กลงกว่าผลการวัดของผู้สังเกตอีกคนหนึ่ง (ตัวอย่างเช่น ladder paradox เกี่ยวข้องกับบันไดยาวซึ่งเคลื่อนที่ด้วยอัตราเร็วใกล้แสงและเข้าเก็บในห้องซึ่งเล็กกว่า)
- การรวมความเร็ว - ความเร็ว (และอัตราเร็ว) ไม่ได้ 'รวม' กันง่าย ๆ ยกตัวอย่างเช่นถ้าจรวดลำหนึ่งกำลังเคลื่อนที่ด้วยอัตราเร็ว ⅔ ของอัตราเร็วแสงสัมพัทธ์กับผู้สังเกตคนหนึ่ง แล้วจรวดก็ปล่อยมิสไซล์ที่มีอัตราเร็วเท่ากับ ⅔ ของอัตราเร็วแสงสัมพัทธ์กับจรวด มิสไซล์ไม่ได้มีอัตราเร็วมากกว่าอัตราเร็วแสงสัมพัทธ์กับผู้สังเกต (ในตัวอย่างนี้ ผู้สังเกตจะเห็นมิสไซล์วิ่งไปด้วยอัตราเร็ว 12/13 ของอัตราเร็วแสง)
- ความเฉื่อยกับโมเมนตัม - เมื่อความเร็วของวัตถุเข้าใกล้อัตราเร็วแสง วัตถุจะเร่งได้ยากขึ้นและยากขึ้นเรื่อย ๆ
- การสมมูลของมวลและพลังงาน, E=mc2 - มวลและพลังงานสามารถแปลงกลับกันไปมา และมีบทบาทเทียบเท่ากัน (ตัวอย่างเช่น แรงโน้มถ่วงของแอปเปิลที่กำลังหล่น ส่วนหนึ่งเกิดจากพลังงานจลน์ของอนุภาคย่อยซึ่งประกอบเป็นแอปเปิลขึ้นมา)
กรอบอ้างอิง ระบบพิกัด และการแปลงแบบลอเรนซ์[แก้]

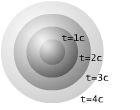
ในภาพเคลื่อนไหว แกนในแนวดิ่งหมายถึง เวลา ส่วนแกนแนวนอนหมายถึง ระยะทาง เส้นประคือวิถีของกาลอวกาศ ("world line") ของผู้สังเกต ภาพส่วนล่างของไดอะแกรมแสดงเหตุการณ์ที่ผู้สังเกตมองเห็น ภาพส่วนบนแสดง light cone หรือสิ่งที่ผู้สังเกตจะมองเห็น จุดเล็ก ๆ ในรูปคือเหตุการณ์แบบสุ่มที่อาจเกิดขึ้นได้ในกาลอวกาศ
เส้นลาดของ world line (ที่เบี่ยงเบนไปจากแนวดิ่ง) แสดงถึงความเร็วสัมพัทธ์กับผู้สังเกต พึงพิจารณามุมมองของกาลอวกาศที่เปลี่ยนแปลงไปเมื่อผู้สังเกตเร่งความเร็วขึ้น
ทฤษฎีสัมพัทธภาพขึ้นอยู่กับ "กรอบอ้างอิง" กรอบอ้างอิงคือจุดในปริภูมิที่อยู่นิ่ง หรือเคลื่อนที่ด้วยความเร็วคงที่ จากตำแหน่งซึ่งสามารถวัดได้ตามแกน 3 แกน นอกจากนี้ กรอบอ้างอิงยังมีนาฬิกาซึ่งกำลังเคลื่อนที่ไปกับกรอบอ้างอิงซึ่งใช้ในการวัดเวลาของเหตุการณ์
เหตุการณ์ คือสิ่งที่เกิดขึ้นโดยสามารถระบุเป็นเวลาและตำแหน่งเดี่ยว ๆ ในปริภูมิสัมพัทธ์กับกรอบอ้างอิง: นั่นคือ "จุด" ในปริภูมิ-เวลา เนื่องจากอัตราเร็วแสงมีค่าคงที่ในแต่ละกรอบอ้างอิงและทุก ๆ กรอบ พัลส์ของแสงจึงสามารถใช้วัดระยะทางได้อย่างแม่นยำและกลับมาเมื่อครั้งที่เหตุการณ์เกิดขึ้นไปยังนาฬิกา ถึงแม้ว่าแสงจะใช้เวลากลับมาหานาฬิกาหลังจากที่เหตุการณ์ได้เกิดขึ้นแล้วก็ตาม
ยกตัวอย่างเช่น การระเบิดของประทัดสามารถเป็น "เหตุการณ์" ได้ เราสามารถระบุเหตุการณ์ได้อย่างสมบูรณ์ด้วยใช้พิกัด ปริภูมิ-เวลา 4 มิติ: เวลาที่เหตุการณ์เกิดขึ้น และตำแหน่ง 3 มิติจากตำแหน่งอ้างอิง เรียกกรอบอ้างอิงนี้ว่า S
ในทฤษฎีสัมพัทธภาพ เรามักต้องการคำนวณตำแหน่งของจุดจากตำแหน่งอ้างอิงอีกอันหนึ่ง
สมมุติเรามีกรอบอ้างอิงที่สอง คือ S' ซึ่งมีแกนพิกัดและนาฬิกาวางตัวทับกันกับระบบของ S ที่เวลาเป็นศูนย์ แต่กรอบอ้างอิงที่สองกำลังเคลื่อนที่ด้วยความเร็วคงที่ เทียบกับกรอบอ้างอิง S ไปตามแกน
เนื่องจากไม่มีกรอบอ้างอิงสัมบูรณ์ในทฤษฎีสัมพัทธภาพ แนวคิดเรื่อง 'การเคลื่อนที่' จึงไม่ได้มีอยู่อย่างชัดเจน จากที่ทุกสิ่งย่อมเคลื่อนที่เทียบกับกรอบอ้างอิงอื่นเสมอ แทนที่โดย กรอบสองกรอบใด ๆ ที่เคลื่อนที่ด้วยอัตราเร็วเท่ากัน ในทิศทางเดียวกันจะเรียกว่า การเคลื่อนที่ร่วม ดังนั้น S และ S' จึงไม่ได้เป็นการเคลื่อนที่ร่วมกัน
กำหนดให้ เหตุการณ์ เกิดขึ้นในพิกัดปริภูมิ-เวลา ในระบบ S และในพิกัด ในระบบ S' จากนั้นการแปลงแบบลอเรนซ์ระบุว่าพิกัดทั้งสองสัมพันธ์กันดังนี้:
เมื่อ เรียกว่า Lorentz factor และ คือ อัตราเร็วแสง ในสุญญากาศ
พิกัด และ ไม่ได้รับผล แต่แกน และ นั้นผสานกันในสูตรการแปลง โดยการแปลงนี้สามารถเข้าใจได้ด้วย การหมุนแบบไฮเพอร์โบลิก
ปริมาณซึ่งไม่แปรเปลี่ยนภายใต้การแปลงแบบลอเรนซ์รู้จักกันในนาม Lorentz scalar
ความพร้อมกัน[แก้]
จากสมการที่หนึ่งของการแปลงแบบลอเรนซ์ในเทอมผลต่างของพิกัด จะได้
เห็นได้ชัดว่าเหตุการณ์สองอย่างที่พร้อมกันในกรอบอ้างอิง S (คือ ) นั้นไม่จำเป็นต้องเกิดขึ้นพร้อมกันในอีกกรอบอ้างอิงหนึ่งซึ่งในที่นี้ก็คือ กรอบอ้างอิง S' (คือ ). เหตุการณ์ทั้งสองนั้นจะเกิดขึ้นพร้อมกันในกรอบอ้างอิง S'ด้วยก็ต่อเมื่อเหตุการณ์เหล่านั้นเกิดขึ้น ณ ตำแหน่งเดียวกันในกรอบอ้างอิง S (คือ )
การยืดออกของเวลา และการหดสั้นของความยาว[แก้]
จากการเขียนการแปลงแบบลอเรนซ์และอินเวอร์สในเทอมผลต่างของพิกัด เราจะได้
และ
สมมุติว่าเรามีนาฬิกาซึ่งอยู่นิ่งในกรอบอ้างอิง S เสียงติ๊กสองติ๊กของนาฬิกาวัดโดยที่ ถ้าเราต้องการรู้ความสัมพัทธ์ระหว่างเวลากับเสียงติ๊ก ซึ่งวัดโดยระบบอ้างอิงทั้งสอง เราสามารถใช้สมการแรกและพบว่า
นี่แสดงให้เห็นว่า ช่วงเวลา ระหว่างเสียงนาฬิกาสองติ๊กที่วัดในกรอบอ้างอิงซึ่ง 'เคลื่อนที่' S' นั้นโตกว่าช่วงเวลา ระหว่างเสียงนาฬิกาสองติ๊กที่วัดในกรอบอ้างอิงในกรอบที่หยุดนิ่งเทียบกับนาฬิกานั้น ปรากฏการณ์ดังกล่าวเรียกว่า การยืดออกของเวลา (ข้อสังเกต: การวัดเวลาระหว่างสองเหตุการณ์ใด ๆ จะต้องวัดที่ตำแหน่งในปริภูมิเดิมเสมอเทียบกับกรอบอ้างอิงนั้น ๆ คือ ในกรอบอ้างอิง S หรือ ในกรอบอ้างอิง S' :ผู้แปล)
เช่นเดียวกัน สมมุติเรามีไม้วัดวางนิ่งอยู่ในกรอบอ้างอิง S ในระบบนี้ ความยาวของไม้สามารถเขียนเป็น ถ้าเราต้องการหาความยาวของไม้นี้โดยวัดในกรอบอ้างอิงซึ่ง 'เคลื่อนที่' S' เราต้องมั่นใจว่าวัดระยะ ที่ตำแหน่งปลายไม้อย่างพร้อมกันในกรอบอ้างอิง S' หรือพูดอีกอย่างก็คือ การวัดต้องให้ ซึ่งเราสามารถรวมหลักการนี้เข้ากับสมการที่สี่เพื่อหาความสัมพันธ์ระหว่างความยาว กับ ได้เป็น:
นี่แสดงว่าความยาว ของไม้ซึ่งวัดในกรอบอ้างอิงซึ่ง 'เคลื่อนที่' S' สั้นกว่าความยาว ในกรอบที่อยู่นิ่งเทียบกับตัวไม้เอง ปรากฏการณ์นี้เรียกว่า การหดสั้นของความยาว หรือ การหดสั้นแบบลอเรนซ์ (ข้อสังเกต: การวัดความยาวระหว่างสองตำแหน่งในปริภูมิจะต้องวัดที่เวลาเดียวกันเสมอเทียบกับกรอบอ้างอิงนั้น ๆ คือ ในกรอบอ้างอิง S หรือ ในกรอบอ้างอิง S' :ผู้แปล)
ผลการยืดหดเหล่านี้ไม่ใช่เพียงภาพปรากฏเท่านั้น แต่มันสัมพันธ์อย่างชัดเจนกับวิธีในการวัดช่วงเวลาระหว่างเหตุการณ์ 'ร่วมตำแหน่ง' และระยะทางระหว่างเหตุการณ์ที่เกิดขึ้นอย่างพร้อมกัน
ดูเพิ่ม twin paradox
Causality และการห้ามวัตถุเคลื่อนที่เร็วกว่าแสง[แก้]

ในแผนภาพที่ 2 ช่วง AB เรียกว่า 'time-like' กล่าวคือ มีกรอบอ้างอิงซึ่งมีเหตุการณ์ A และเหตุการณ์ B เกิดขึ้นในตำแหน่งเดียวกันในปริภูมิ แต่แยกกันเนื่องจากการเกิดขึ้นในเวลาที่ต่างกันเท่านั้น ถ้า A เกิดก่อน B ในกรอบอ้างอิงนั้น A ย่อมเกิดขึ้นก่อน B ในทุก ๆ กรอบอ้างอิง จึงเป็นไปได้ในเชิงสมมติฐานว่า สสาร (หรือข้อมูล) จะสามารถเคลื่อนที่จาก A ไป B และมีความสัมพันธ์อย่างมีเหตุผล (โดย A เป็นเหตุ และ B เป็นผล)
ช่วง AC ในแผนภาพเรียกว่า 'space-like'; กล่าวคือ มีกรอบอ้างอิงซึ่งเหตุการณ์ A และเหตุการณ์ C เกิดขึ้นพร้อมกัน เว้นแต่ว่าอยู่คนละตำแหน่งในปริภูมิ อย่างไรก็ตามยังมีบางกรอบซึ่ง A เกิดก่อน C (ดังรูป) และบางกรอบซึ่ง C เกิดก่อน A ถ้าความสัมพันธ์แบบเหตุและผลนั้นเป็นไปได้ระหว่างเหตุการณ์ A และ C พาราดอกซ์ทางตรรกะ (logical paradoxes) จะเกิดขึ้น ตัวอย่างเช่น ถ้า A เป็นเหตุ และ C เป็นผล ก็จะมีบางกรอบอ้างอิงที่ทำให้ผลมาก่อนเหตุ วิธีหนึ่งที่จะมองคือว่า ถ้ามีเทคโนโลยีที่ยอมให้มีการเคลื่อนที่เร็วกว่าแสง มันก็จะทำตัวเป็นไทม์แมชชีน (time machine) ดังนั้นผลสรุปอย่างหนึ่งของทฤษฎีสัมพัทธภาพพิเศษคือว่า (โดยถือว่า causality เป็นหลักการทางตรรกะอย่างหนึ่ง) ไม่มีข้อมูลหรือวัตถุใดสามารถเคลื่อนที่ได้เร็วกว่าแสง อย่างไรก็ตาม สถานการณ์ทางตรรกะไม่ชัดเจนนักในกรณีของทฤษฎีสัมพัทธภาพทั่วไป ดังนั้นจึงเป็นคำถามปลายเปิดว่ามี fundamental principle ซึ่งรักษาหลัก causality (และรักษาหลักการเคลื่อนที่เร็วกว่าแสง) ในทฤษฎีสัมพัทธภาพทั่วไปหรือไม่
การรวมความเร็ว[แก้]
ถ้าผู้สังเกตในกรอบอ้างอิง เห็นวัตถุหนึ่งเคลื่อนที่ไปตามแนวแกน ด้วยความเร็ว ผู้สังเกตในกรอบ จะเห็นว่าวัตถุดังกล่าวมีความเร็ว โดยที่
- .
สมการนี้สามารถหาได้จากการแปลงปริภูมิและเวลาข้างต้น ระลึกไว้ว่าถ้าวัตถุเคลื่อนที่ด้วยอัตราเร็วแสงในกรอบอ้างอิง (นั่นคือ ) วัตถุนั้นก็จะเคลื่อนที่ด้วยอัตราเร็วแสงในกรอบอ้างอิง เช่นกัน ถ้าทั้ง และ เล็กมากเมื่อเทียบกับอัตราเร็วแสง เราก็จะสามารถใช้การแปลงความเร็วแบบกาลิเลียนในแบบสัญชาตญาณของเรา คือ .
มวล โมเมนตัม และพลังงาน[แก้]
นอกจากการปรับเปลี่ยนแนวคิดเกี่ยวกับปริภูมิและเวลาแล้ว ทฤษฎีสัมพัทธภาพยังบังคับให้เราต้องกลับมาพิจารณาแนวคิดของ มวล โมเมนตัม และ พลังงาน ทั้งหมดนี้มีความสำคัญต่อโครงสร้างใน กลศาสตร์นิวตัน ทฤษฎีสัมพัทธภาพแสดงให้เห็นว่า อันที่จริงแล้ว แนวคิดเหล่านั้นมีแง่มุมที่ต่างกันมากสำหรับปริมาณทางกายภาพเดียวกันเหมือนกับที่มันแสดงว่าปริภูมิกับเวลามีความเชื่อมโยงกัน
มีหลายวิธี (ที่เทียบเท่ากัน) ที่จะนิยามโมเมนตัมและพลังงานใน SR (หมายถึง ทฤษฎีสัมพัทธภาพพิเศษ :ผู้แปล) วิธีหนึ่งคือใช้ กฎการอนุรักษ์ ถ้ากฎเหล่านี้ยังคงใช้ได้ใน SR พวกมันย่อมเป็นจริงในทุกกรอบอ้างอิงที่เป็นไปได้ อย่างไรก็ตาม ถ้าเราทำ การทดลองในความคิด อย่างง่ายโดยใช้การนิยามแบบนิวตันของโมเมนตัมและพลังงาน เราจะเห็นว่าปริมาณเหล่านั้นไม่อนุรักษ์ใน SR เราสามารถกู้แนวคิดของการอนุรักษ์กลับมาโดยทำการปรับนิยามเพื่อให้เข้ากับความเร็วเชิงสัมพัทธภาพ และนี่คือนิยามใหม่ซึ่งแก้ไขแล้วสำหรับโมเมนตัมและพลังงานใน SR
ให้วัตถุมี มวลไม่แปรเปลี่ยน m0 เคลื่อนที่ด้วยความเร็ว v พลังงานและโมเมตัมจะเป็น (และถูกสั่งให้เป็น)
เมื่อ γ (Lorentz factor) มาจาก
และ c คืออัตราเร็วแสง เทอม γ ปรากฏอยู่บ่อย ๆ ในทฤษฎีสัมพัทธภาพ และมันมาจาก สมการการแปลงแบบลอเรนซ์
พลังงานและโมเมนตัมเชิงสัมพัทธภาพมีความสัมพันธ์กันตามสูตร
ซึ่งเรียกว่าเป็น สมการพลังงาน-โมเมนตัมเชิงสัมพัทธภาพ (relativistic energy-momentum equation)
สำหรับความเร็วที่น้อยกว่าของแสงมาก ค่า γ สามารถประมาณได้โดยใช้ Taylor series expansion และจะพบว่า
ถ้าไม่มีเทอมแรกในสูตรพลังงาน (จะกล่าวถึงภายหลัง) สูตรเหล่านี้จะสอดคล้องอย่างชัดเจนกับนิยามมาตรฐานของ พลังงานจลน์ และโมเมนตัมแบบนิวตัน นี่เป็นการแสดงว่าทฤษฎีสัมพัทธภาพพิเศษต้องสอดคล้องกับกลศาสตร์นิวตันที่ความเร็วต่ำ
เมื่อดูที่สูตรสำหรับพลังงานข้างต้น เราจะเห็นว่าวัตถุ เมื่ออยู่นิ่ง (v = 0 and γ = 1) จะมีพลังงานที่ไม่เท่ากับศูนย์เหลืออยู่ คือ
พลังงานนี้เรียกว่า พลังงานนิ่ง (rest energy) พลังงานนิ่งไม่ได้เป็นสาเหตุของความขัดแย้งกับทฤษฎีแบบนิวตันเพราะว่ามันเป็นค่าคงที่ และเป็นความแตกต่างในแง่พลังงานซึ่งมีความหมายอย่างยิ่ง ตราบเท่าที่ยังพิจารณาพลังงานจลน์
เมื่อนำสูตรนี้พิจารณาค่า เราจะพบว่าในทฤษฎีสัมพัทธภาพ มวลเป็นเพียงแค่พลังงานรูปแบบหนึ่ง ในปี ค.ศ. 1927 ไอน์สไตน์ได้ตั้งข้อสังเกตเกี่ยวกับทฤษฎีสัมพัทธภาพพิเศษไว้ว่า
ภายใต้ทฤษฎีนี้ มวลนั้นไม่ใช่ปริมาณใหม่อะไร แต่เป็นเพียงปริมาณที่ขึ้นอยู่กับ (และจริง ๆ แล้ว คือ เหมือนกับ) พลังงาน [1]
สูตรนี้มีความสำคัญเมื่อมีคนวัดมวลนิวคลิไอของอะตอมต่าง ๆ และโดยการดูผลต่างของมวลเหล่านั้น ก็สามารถทำนายได้ว่านิวคลีไอใดมีพลังงานที่เก็บไว้จนสามารถเกิด ปฏิกิริยานิวเคลียร์ ได้ รวมทั้งข้อมูลซึ่งมีประโยชน์อย่างยิ่งในการพัฒนา ระเบิดนิวเคลียร์ ผลกระทบของสมการนี้ต่อผู้คนใน ศตวรรษที่ 20 ทำให้มันเป็นหนึ่งในสมการที่มีชื่อเสียงที่สุดในสาขาวิทยาศาสตร์ทั้งหมด
มวลเชิงสัมพัทธภาพ[แก้]
ในวิชาฟิสิกส์เบื้องต้นและหนังสือเก่า ๆ เกี่ยวกับทฤษฎีสัมพัทธภาพบางครั้งจะนิยามคำว่า มวลเชิงสัมพัทธภาพ ซึ่งเพิ่มขึ้นเมื่อความเร็วของวัตถุเพิ่มขึ้น ตามการตีความทางเรขาคณิตของทฤษฎีสัมพัทธภาพพิเศษ มักจะไม่ชอบนิยามนี้ และคำว่า 'มวล' ถูกสงวนไว้สำหรับว่าคำว่า 'มวลนิ่ง' และไม่ขึ้นอยู่กับกรอบอ้างอิง กล่าวคือ มัน ไม่แปรเปลี่ยน
จากการใช้นิยามของมวลเชิงสัมพัทธภาพ มวลวัตถุสามารถแปรเปลี่ยนได้ขึ้นอยู่กับกรอบอ้างอิงเฉื่อยของผู้สังเกตเช่นเดียวกับปริมาณอื่น ๆ เช่น ความยาว การนิยามปริมาณหนึ่ง ๆ บางครั้งมี ประโยชน์ ในการช่วยให้คำนวณง่ายขึ้นโดยจำกัดมันกับกรอบอ้างอิง ยกตัวอย่างเช่น ในการพิจารณาวัตถุซึ่งมีมวลไม่แปรเปลี่ยน m0 ซึ่งเคลื่อนที่ด้วยความเร็วค่าหนึ่งสัมพัทธ์กับกรอบอ้างอิงของผู้สังเกตคนหนึ่ง ผู้สังเกตคนนั้นจะนิยาม มวลเชิงสัมพัทธภาพ ของวัตถุเท่ากับ
"มวลเชิงสัมพัทธภาพ" ไม่ควรสับสนกับนิยามของ "longitudinal" และ "transverse mass" ที่ถูกใช้ในช่วงปี ค.ศ. 1900 และที่ตั้งอยู่บนการประยุกต์ที่ขัดแย้งกันของกฎนิวตัน คือใช้ F=ma สำหรับมวลแปรค่าได้ ในขณะที่มวลเชิงสัมพัทธภาพสัมพันธ์กับมวลเชิงไดนามิกของนิวตัน โดยที่ p=mv และ F=dp/dt
ควรระลึกไว้เช่นกันว่า วัตถุ ไม่ ได้มีมวลมากขึ้นในกรอบอ้างอิง แท้และกรอบอ้างอิงเฉื่อยอื่นๆ (คือ กรอบอ้างอิงที่เห็นวัตถุหยุดนิ่ง :ผู้แปล,หรือกรอบที่เห็นวัตถุเคลื่อนที่ด้วยความเร็วคงที่) เพราะมวลเชิงสัมพัทธภาพจะแตกต่างกันไปสำหรับผู้สังเกตในกรอบต่าง ๆ กัน(แท้จริงแล้วคือ Lorentz factor มีค่าต่าง ๆ กัน) มวลที่อิสระจากกรอบ เท่านั้น จึงจะเป็นมวลไม่แปรเปลี่ยน (มวลชิงสัมภัทธภาพ เปลี่ยนไปตามกรอบอ้างอิง แต่ไม่มีความจำเป็นที่จะนิยาม มวลเชิงสัมพัทธภาพขึ้นมาเลย)เมื่อใช้มวลเชิงสัมพัทธภาพ กรอบอ้างอิงที่ใช้ต้องระบุให้ชัดเจนหากมันไม่ชัดเจนหรือแสดงออกมา มันเป็นไปโดยไม่ได้กล่าวว่า การเพิ่มขึ้นในมวลเชิงสัมพัทธภาพไม่ได้มาจากจำนวนอะตอมที่เพิ่มขึ้นในวัตถุ แต่แทนที่จะเป็นอย่างนั้น มวลเชิงสัมพัทธภาพของแต่ละอะตอมและอนุภาคเล็กกว่าอะตอมก็ไม่เพิ่มขึ้น แต่พลังงานในการเคลื่อนที่เพิ่มขึ้น และเราตีความว่ามวลคือพลังงานนั่นเองแท้จริงแล้วธรรมชาติของมวลและพลังงานต่างกันมาก
หนังสือเรียนฟิสิกส์เก่า ๆ บางครั้งจะใช้มวลเชิงสัมพัทธภาพเพราะมันยอมให้นักเรียนได้ใช้ความรู้ของฟิสิกส์แบบนิวตันเพื่อจะได้เข้าใจในทฤษฎีสัมพัทธภาพในกรอบอ้างอิงของตัวเลือก (ซึ่งมักจะเป็นของตัวเอง!) "มวลเชิงสัมพัทธภาพ" ยังสอดคล้องกับแนวคิดของ "การยืดออกของเวลา" และ "การหดสั้นของระยะทาง"
แรง[แก้]
นิยามแบบคลาสสิกของแรง F กำหนดโดย กฎข้อที่สองของนิวตัน ในรูปแบบดั้งเดิม
และใช้ได้ในทฤษฎีสัมพัทธภาพ
หนังสือเรียนสมัยใหม่ มักจะเขียนกฎข้อที่สองของนิวตันใหม่เป็น
รูปแบบนี้ใช้ไม่ได้ในทฤษฎีสัมพัทธภาพและกรณีอื่นใดที่มวล m แปรเปลี่ยน
สำหรับมวลคงที่ m0 สูตรดังกล่าวสามารถเขียนแทนได้ ในกรณีสัมพัทธภาพ จะเป็น
จากการมองสมการนี้ จะพบว่าแรงและเวกเตอร์ความเร่งไม่เป็นจำเป็นต้องขนานกันในทฤษฎีสัมพัทธภาพ
เรขาคณิตของปริภูมิ-เวลา[แก้]
ทฤษฎีสัมพัทธภาพพิเศษใช้ปริภูมิ-เวลาแบบมินคอฟสกีสี่มิติแบบราบ ซึ่งเป็นตัวอย่างหนึ่งของ ปริภูมิ-เวลา อย่างไรก็ตาม ปริภูมิแบบนี้คล้ายกับปริภูมิแบบยูคลิดสามมิติมาตรฐานอย่างมาก และโชคดีคือว่าด้วยเหตุนั้น มันง่ายมากที่จัดการกับมัน
ผลต่างเชิงอนุพันธ์ของระยะทาง(ds) ในปริภูมิสามมิติแบบคาร์ทีเซียน นิยามโดย
เมื่อ เป็นผลต่างเชิงอนุพันธ์ของมิติตามแกนทั้งสาม ในเรขาคณิตของทฤษฎีสัมพัทธภาพ มิติที่สี่ คือ เวลา ได้ถูกเพิ่มเข้าไป พร้อมกับหน่วยของ c นั่นทำให้สมการสำหรับดิฟเฟอเรนเชียลของระยะทาง กลายเป็น
ถ้าเราอยากทำให้พิกัดของเวลาดูเหมือนพิกัดของปริภูมิ เราสามารถทำให้เวลาเป็นจำนวนจินตภาพ: x4 = ict . ในกรณีนี้ สมการข้างต้นจะสมมาตร
นี่แสดงให้เห็นมุมมองทางทฤษฎีที่ลึกซึ้งเมื่อมันแสดงว่าทฤษฎีสัมพัทธภาพเป็นการ สมมาตรเชิงหมุน ของ ปริภูมิ-เวลา ซึ่งคล้ายกับสมมาตรเชิงหมุนของ ปริภูมิแบบยูคลิด อย่างมาก หากเป็นปริภูมิแบบยูคลิดจะใช้ Euclidean metric ดังนั้นปริภูมิ-เวลาจะใช้ Minkowski metric ตาม Misner (1971 §2.3) แล้ว ความเข้าใจในเชิงลึกทั้งหมดของทั้งทฤษฎีสัมพัทธภาพพิเศษและทั่วไปจะมาจากการศึกษา Minkowski metric (จะบรรยายในภายหลัง) มากกว่า Euclidean metric "ปลอม" ที่ใช้ ict เป็นพิกัดเวลา
ถ้าเราลดแกนของปริภูมิลงเป็น 2 จนทำให้เราสามารถใช้ฟิสิกส์ในปริภูมิ 3 มิติ
เราจะเห็นว่า null geodesics จะวางตัวตามกรวยคู่
ซึ่งนิยามโดยสมการ
หรือ
ซึ่งเป็นสมการของวงกลมซึ่ง r=c*dt ถ้าเราขยายผลนี้เป็นปริภูมิสามมิติ null geodesics จะเป็นกรวย 4 มิติ
null dual-cone นี้แทน "แนวการมองเห็น" ของจุดในปริภูมิ กล่าวคือ เมื่อเรามองไปที่ดวงดาวและกล่าวว่า "แสงจากดาวที่ฉันรับได้มีอายุ X ปี" หมายความว่าเรากำลังมองลงไปตามแนวการมองเห็นนี้ คือ null geodesic เรากำลังมองเหตุการณ์หนึ่งที่ห่างออกไป เมตร และ d/c วินาทีในอดีต ด้วยเหตุผลดังกล่าว null dual cone จึงรู้จักกันในนาม 'กรวยแสง' (จุดในมุมซ้ายล่างของภาพแทนดวงดาว จุดกำเนิดแทนตัวผู้สังเกต และเส้นเชื่อมนั้นแทน null geodesic "แนวการมองเห็น")
กรวยในเขต -t เป็นข้อมูลที่จุดนั้นกำลัง 'รับ' ในขณะที่กรวยในเขต +t เป็นข้อมูลที่จุดนั้นกำลัง 'ส่ง'
เรขาคณิตของปริภูมิ-เวลาแบบมินคอฟสกี สามารถพรรณนาได้โดยใช้ Minkowski diagrams ซึ่งมีประโยชน์เช่นกันในความเข้าใจการทดลองทางความคิดต่าง ๆ ในทฤษฎีสัมพัทธภาพพิเศษ
ฟิสิกส์ในปริภูมิ-เวลา[แก้]
บัดนี้ เราจะได้เห็นวิธีการเขียนสมการของทฤษฎีสัมพัทธภาพพิเศษในรูปแบบที่ไม่แปรเปลี่ยนอย่างชัดเจน ตำแหน่งของเหตุการณ์หนึ่ง ๆ ในปริภูมิ-เวลา สามารถกำหนดโดย contravariant four vector ซึ่งมีองค์ประกอบ คือ
หมายความว่า และ และ และ . ตัวยกเป็นดัชนีของ contravariant indices ในส่วนนี้มากกว่าจะเป็นเลขชี้กำลังเว้นเสียแต่ว่าเมื่อมันหมายถึงยกกำลังสอง ส่วนตัวห้อยเป็น covariant indices ซึ่งเรียงจากศูนย์ไปถึงสามเมื่อใช้กับ spacetime gradient ของสนาม φ:
เมตริกซ์และการแปลงพิกัด[แก้]
จากการระลึถึงธรรมชาติสี่มิติของปริภูมิ-เวลา เราถูกชักจูงให้สร้าง Minkowski metric, η, กำหนดให้มีองค์ประกอบ (ใช้ได้ใน กรอบอ้างอิงเฉื่อย ใด ๆ) คือ
และส่วนกลับของมันคือ
ภายใต้เงื่อนไข
จากนั้น เราระลึกได้ว่าการแปลงพิกัดระหว่างกรอบอ้างอิงเฉื่อยนั้นกำหนดโดย Lorentz transformation tensor Λ. สำหรับกรณีพิเศษของการเคลื่อนที่ตามแนวแกน x เราจะได้
หรือ
ซึ่งก็คือ matrix of a boost (เช่นการหมุน) ระหว่างพิกัด x กับ t เมื่อ μ' บอกแถว และ ν บอกคอลัมน์ ค่า β และ γ ยังนิยามเป็น
เพื่อให้ทั่วไปยิ่งขึ้น การแปลงจากกรอบอ้างอิงหนึ่ง (ซึ่งไม่สนการแปลงเพื่อความเรียบง่าย) ไปยังอีกกรอบ ต้องทำให้
เมื่อมี implied summation ของ และ จาก 0 ถึง 3 บนหลักมือขวาซึ่งสอดคล้องกับ Einstein summation convention Poincaré group เป็นกลุ่มที่ทั่วไปที่สุดของการแปลงซึ่งยังคงรักษาi Minkowski metric ไว้ และนี่เป็นสมมาตรทางกายภาพภายใต้ทฤษฎีสัมพัทธภาพอีกด้วย
ปริมาณทางกายภาพแท้ทั้งหมดกำหนดโดยเทนเซอร์ ดังนั้นเพื่อการแปลงกรอบหนึ่งไปยังอีกกรอบหนึ่ง เราใช้จะกฎที่รู้จักกันดีในชื่อ tensor transformation law
เมื่อ เป็นเมตริกซ์ส่วนกลับของ .
เพื่อให้เห็นว่ามันมีประโยชน์อย่างไร เราจะแปลงตำแหน่งของเหตุการณ์หนึ่งจากระบบพิกัดไม่มีเครื่องหมายไพรม์ S ไปยังระบบมีไพรม์ S' เราคำนวณได้ว่า
ซึ่งการแปลงแบบลอเรนซ์ให้ผลเหมือนกัน เทนเซอร์ทุกตัวแปลงด้วยกฎเดียวกัน
ความยาวกำลังสองของดิฟเฟอเรนเชียลของ position four-vector ซึ่งหาได้โดย
เป็นปริมาณไม่แปรเปลี่ยน การไม่แปรเปลี่ยนหมายความว่ามันให้ค่าเดิมเสมอในทุกกรอบอ้างอิงเฉื่อย เพราะมันเป็นสเกลาร์ (0 rank tensor) และดังนั้นจึงไม่มี Λ ปรากฏในการแปลงเล็ก ๆ น้อย ๆ ระลึกไว้ว่าเมื่อ line element เป็นลบ จะเป็นดิฟเฟอเรนเชียลของ proper time ในขณะที่ เมื่อ เป็นบวก จะเป็นดิฟเฟอเรนเชียลของ proper distance
ค่าพื้นฐานของการจัดรูปสมการทางฟิสิกส์ในรูปของเทนเซอร์ คือสิ่งที่ไม่แปรเปลี่ยนภายใต้the Poincaré group อย่างชัดเจน จนทำให้เราไม่จำเป็นต้องทำการคำนวณเพิ่มเติมที่น่าเบื่อหน่ายเพื่อตรวจสอบความจริงนี้ เช่นเดียวกับการสร้างสมการ เรามักพบว่าสมการที่ตอนแรกดูจะไม่เกี่ยวข้องกันนั้น อันที่จริงแล้ว มันมีความสัมพันธ์อย่างใกล้ชิดในการเป็นส่วนหนึ่งของสมการเทนเซอร์เดียวกัน
ความเร็วและความเร่งใน 4 มิติ[แก้]
การเขียนปริมาณทางกายภาพอื่น ๆ เป็นเทนเซอร์สามารถนำมาซึ่งกฎการแปลงได้เรียบง่ายขึ้นเช่นกัน อย่างแรก ระลึกไว้ว่า velocity four-vector Uμ กำหนดโดย
จากการเขียนเช่นนี้ เราสามารถกลับมามองกฎการรวมความเร็วในรูปแบบอย่างง่ายเกี่ยวกับการแปลง velocity four-vector ของอนุภาคจากกรอบอ้างอิงหนึ่งไปยังอีกกรอบหนึ่ง Uμ จึงมีรูปแบบไม่แปรเปลี่ยน คือ
ดังนั้น velocity four-vector ทุกตัวจึงมีขนาดเท่ากับ c นี่เป็นสิ่งที่บอกความจริงว่าไม่มีวัตถุใดอยู่นิ่งในสัมพัทธภาพ อย่างน้อยที่สุด คุณก็ต้องเคลื่อนที่ไปในเวลา acceleration 4-vector กำหนดโดย . เมื่อได้ดังนั้น ทำการ differentiate สมการข้างต้นด้วย τ จะได้
ดังนั้นในทฤษฎีสัมพัทธภาพ acceleration four-vector กับ velocity 4-vector ตั้งฉากกัน
โมเมนตัมใน 4 มิติ[แก้]
โมเมนตัมและพลังงานรวมอยู่ใน covariant 4-vector:
เมื่อ m คือ มวลไม่แปรเปลี่ยน
ปริมาณไม่แปรเปลี่ยน (invarient) ของ momentum 4-vector คือ:
เราสามารถทำออกมาได้ว่า ค่าไม่แปรเปลี่ยนนี้ เนื่องจากมันเป็นสเกลาร์ จึงไม่เกี่ยวข้องกับว่าเราใช้กรอบอ้างอิงไหนในการคำนวณ หลังจากนั้นโดยการแปลงกรอบที่ทำให้โมเมนคัมรวมเป็นศูนย์
เราจะพบว่า พลังงานนิ่งเป็นค่าไม่แปรเปลี่ยนซึ่งไม่ขึ้นอยู่กับกรอบอ้างอิง พลังงานนิ่งสามารถคำนวณได้แม้ในระบบที่อนุภาคและระบบกำลังเคลื่อนที่ เพียงแปลงกรอบไปยังกรอบที่ทำให้โมเมนตัมเป็นศูนย์เท่านั้น
พลังงานนิ่งสัมพันธ์กับมวลตามสมการอันน่ายินดีที่เราได้พูดถึงไปแล้ว
ระลึกไว้ว่า มวลของระบบวัดในกรอบศูนย์กลางของโมเมนตัม (center of momentum frame) (เมื่อโมเมนตัมลัพธ์เป็นศูนย์) นั้นกำหนดโดยพลังงานรวมของระบบในกรอบอ้างอิงนั้น มันไม่ได้เท่ากับผลรวมของมวลแต่ละก้อนที่วัดในกรอบอ้างอิงอื่น
แรงใน 4 มิติ[แก้]
เมื่อใช้ กฎข้อที่สามของนิวตัน แรงทั้งสองต้องนิยามจากอัตราการเปลี่ยนแปลงของโมเมนตัมซึ่งใช้พิกัดเวลาเดียวกัน กล่าวคือ เราต้องใช้แรงใน 3 มิติในการนิยามข้างต้น โชคร้ายที่ไม่มีเทนเซอร์ใน 4 มิติใดที่บรรจุองค์ประกอบของเวกเตอร์แรง 3 มิติตามองค์ประกอบต่าง ๆ ของมัน
ถ้าวัตถุไม่ได้เคลื่อนที่ด้วยอัตราเร็ว c เราสามารถแปลงแรงใน 3 มิติจากกรอบอ้างอิงที่เคลื่อนที่ร่วมไปกับวัตถุไปยังกรอบอ้างอิงของผู้สังเกตได้ นั่นนำมาซึ่ง 4-vector ซึ่งเรียกว่า four-force มันคืออัตราการเปลี่ยนแปลงของ four-vector พลังงาน-โมเมนตัม เทียบกับ proper time รูป covariant version ของ four force คือ
เมื่อ คือ proper time
ในกรอบนิ่งของวัตถุ องค์ประกอบเวลาของ four force จะเป็นศูนย์จนกว่า "มวลไม่แปรเปลี่ยน" ของวัตถุนั้นจะเปลี่ยนแปลง โดยที่ มันจะเท่ากับค่าลบของอัตราการเปลี่ยนแปลงคูณ c2 อย่างไรก็ตาม โดยทั่วไปแล้วองค์ประกอบของ four force ไม่ได้เท่ากับองค์ประกอบของแรงสามมิติ เพราะว่าแรงในสามมิตินิยามโดยอัตราการเปลี่ยนแปลงโมเมนตัมเทียบกับเวลาของพิกดันั้น กล่าวคือ ในขณะที่ four force นิยามโดยอัตราการเปลี่ยนแปลงโมเมนตัมเทียบกับ proper time นั่นคือ .
ใน continuous medium density of force3 มิติรวมกับ density of power เพื่อสร้าง covariant 4-vector องค์ประกอบเชิงปริภูมิมาจากผลการหารแรงที่กระทำต่อเซลล์เล็กจิ๋ว (ใน 3 มิติ) โดยปริมาตรของเซลล์นั้น ส่วนองค์ประกอบเชิงเวลามาจากค่าลบของกำลังที่ส่งผ่านไปยังเซลล์หารด้วยปริมาตรของเซลล์นั้น เวกเตอร์นี้จะนำไปใช้ในเรื่องแม่เหล็กไฟฟ้าด้านล่างต่อไป
สัมพัทธภาพกับการรวมสนามแม่เหล็กไฟฟ้า[แก้]
การแปลงแบบลอเรนซ์ของ สนามไฟฟ้า ของประจุซึ่งเคลื่อนที่ไปในกรอบอ้างอิงของผู้สังเกตซึ่งไม่ได้เคลื่อนที่ ให้ผลการปรากฏของเทอมทางคณิตศาสตร์ที่รู้จักกันทั่วไปในนาม สนามแม่เหล็ก ในทางกลับกัน สนาม แม่เหล็กที่เกิดขึ้นจากประจุซึ่งเคลื่อนที่จะหายไปและกลายเป็นสนาม ไฟฟ้าสถิต ทั้งหมดในกรอบอ้างอิงที่เคลื่อนที่ไปกับประจุ สมการของแมกซ์เวลล์ จึงเข้ากันอย่างเห็นไห้ชัดกับผลเชิงสัมพัทธภาพพิเศษในแบบจำลองคลาสสิกของเอกภพ เมื่อสนามไฟฟ้าและสนามแม่เหล็กขึ้นอยู่กับกรอบอ้างอิงและสัมพันธ์กัน จึงเรียกว่าสนาม แม่เหล็กไฟฟ้า ทั้งนี้ทฤษฎีสัมพัทธภาพพิเศษได้ให้กฎการแปลงสำหรับวิธีที่สนามแม่เหล็กไฟฟ้าในกรอบอ้างอิงเฉื่อยหนึ่งไปยังอีกกรอบอ้างอิงเฉื่อยอีกอันหนึ่ง
ทฤษฎีแม่เหล็กไฟฟ้าใน 4 มิติ[แก้]
สมการของแมกซ์เวลล์ ในรูปแบบสามมิตินั้นสอดคล้องกับเนื้อความเชิงกายภาพของทฤษฎีสัมพัทธภาพพิเศษอยู่แล้ว แต่เราต้องเขียนมันใหม่เพื่อทำให้มันมีความไม่แปรเปลี่ยนอย่างชัดเจน
ความหนาแน่นประจุ และความหนาแน่นกระแส สามารถรวมกันใน current-charge 4-vector:
กฎ การอนุรักษ์ประจุ จึงกลายเป็น
สนามไฟฟ้า และ magnetic induction รวมกันใน (rank 2 antisymmetric covariant) electromagnetic field tensor
ความหนาแน่นของ แรงลอเรนซ์ กระทำต่อวัตถุโดยสนามแม่เหล็กไฟฟ้าจะกลายเป็น
กฎการเหนี่ยวนำของฟาราเดย์ และ กฎของเกาส์ สำหรับสนามแม่เหล็กรวมกันในรูป
ถึงแม้ว่าจะมีสมการปรากฏขึ้นถึง 64 สมการในที่นี้ จริง ๆ แล้วมันจะลดลงเหลือเพียงสี่สมการที่ไม่ขึ้นจากกัน โดยการใช้ antisymmetry ของสนามแม่เหล็กไฟฟ้า เราสามารถลดรูปเหลือ identity (0=0) หรือไม่ก็ลบสามารถทั้งหมดออกไปยกเว้นสมาการที่มี λ,μ,ν = 1,2,3 หรือ 2,3,0 หรือ 3,0,1 หรือ 0,1,2.
electric displacement และ magnetic field รวมกันเป็น (rank 2 antisymmetric contravariant) electromagnetic displacement tensor
กฎของแอมแปร์ และ กฎของเกาส์ รวมกันในรูป
ในสุญญากาศ constitutive equations คือ
Antisymmetry ลดสมการทั้ง 16 สมการนี้เหลือเพียงหกสมการที่ไม่ขึ้นจากกัน
ความหนาแน่นพลังงาน ของสนามแม่เหล็กไฟฟ้ารวมกันกับ with Poynting vector และ Maxwell stress tensor เพื่อสร้างเป็น stress-energy tensor 4 มิติ มันคือ (ความหนาแน่น) ฟลักซ์ของ momentum 4-vector ในรูป rank 2 mixed tensor มันสามารถเขียนเป็น
เมื่อ คือ Kronecker delta เมื่อดัชนีตัวบนต่ำกว่า η มันจะสมมาตรและเป็นส่วนหนึ่งของแหล่งกำเนิดสนามโน้มถ่วง
การอนุรักษ์โมเมนตัมเชิงเส้นและพลังงานโดยสนามแม่เหล็กไฟฟ้าสามารถเขียนเป็น
เมื่อ คือความหนาแน่นของ แรงลอเรนซ์ สมการนี้สามารถสรุปได้จากสมการข้างต้นที่ผ่านมา (กับความพยายามอย่างสำคัญ)
สถานะ[แก้]
ดูบทความหลักที่: สถานะของทฤษฎีสัมพัทธภาพพิเศษ
ทฤษฎีสัมพัทธภาพจะถูกต้องเมื่อ ศักย์โน้มถ่วง น้อยกว่า c2 มาก ๆ ในสนามโน้มถ่วงที่เข้ม เราต้องใช้ ทฤษฎีสัมพัทธภาพทั่วไป (ซึ่งกลายเป็นสัมพัทธภาพพิเศษที่สนามอ่อน ๆ) ที่ระดับเล็กมากเช่นที่ระดับ ความยาวพลังค์ และต่ำลงไป ผลทางควอนตัมต้องถูกนำไปใช้พิจารณายังผลใน quantum gravity อย่างไรก็ตาม ที่ระดับโตและในที่ที่ปลอดสนามโน้มถ่วงเข้ม ๆ ทฤษฎีสัมพัทธภาพถูกทดสอบในเชิงทดลองได้ผลถูกต้องในระดับที่แม่นยำมาก (10-14) จึงได้รับการยอมรับจากสังคมฟิสิกส์ในทีสุด ผลการทดลองซึ่งพบว่าขัดแย้งกับทฤษฎีจะไม่อาจอยู่ได้ต่อไป และถูกเชื่อว่าที่เป็นเช่นนั้นเนื่องจากความผิดพลาดของการทดลอง
เนื่องจากความอิสระในการเลือกนิยามหน่วยของความยาวและเวลาในฟิสิกส์ มันจึงเป็นไปได้ที่จะสร้างผลสรุปของนิยามเชิง สัจนิรันดร์ จากหนึ่งในสองของสมมติฐานจากทฤษฎีสัมพัทธภาพ แต่เราไม่สามารถทำสิ่งเหล่านี้สำหรับสมมติฐานสองอย่างพร้อมกัน เพราะเมื่อรวมกัน พวกมันจะให้ผลสรุปซึ่งอิสระจากการเลือกนิยามความยาวและเวลา
ทฤษฎีสัมพัทธภาพนั้นสอดคล้องในตัวเองในเชิงคณิตศาสตร์ และมันเป็นส่วนสำคัญของทฤษฎีเชิงกายภาพยุคใหม่ทั้งหมด เช่น ทฤษฎีสนามควอนตัม, ทฤษฎีสตริง, และทฤษฎีสัมพัทธภาพทั่วไป (ในกรณีจำกัดที่ลืมสนามโน้มถ่วงได้)
กลศาสตร์นิวตันก็สอดคล้องในเชิงคณิตศาสตร์กับทฤษฎีสัมพัทธภาพพิเศษที่ความเร็วน้อย ๆ (เทียบกับอัตราเร็วแสง) ดังนั้นกลศาสตร์นิวตันสามารถพิจารณาเท่ากับทฤษฎีสัมพัทธภาพพิเศษของวัตถุซึ่งเคลื่อนที่ช้าได้ ดู สถานะของทฤษฎีสัมพัทธภาพทั่วไป สำหรับรายละเอียดเพิ่มเติม
การทดลองส่วนหนึ่งที่นำมาซึ่งทฤษฎีสัมพัทธภาพพิเศษ
- การทดลองของ Trouton-Noble แสดงให้เห็นว่าทอร์กของตัวเก็บประจุนั้นไม่ขึ้นอยู่กับตำแหน่งและกรอบอ้างอิงเฉื่อย การทดลองนี้นำมาสู่สมมติฐานข้อแรก
- การทดลองของไมเคิลสัน-เมอร์เลย์ อันโด่งดังแสดงให้เห็นถึงความไม่แปรเปลี่ยนเชิงทิศทางของอัตราเร็วแสงสองทาง — "อัตราเร็วแสง" จึงนิยามเป็นสมมติฐานข้อที่สอง
การทดลองหลายอย่างนำมาสู่การทดสอบทฤษฎีสัมพัทธภาพพิเศษต้านกับทฤษฎีคู่แข่ง รวมทั้งการทดลองเหล่านี้
- การทดลองของ Kaufman — การสะท้อนของอิเล็กตรอนซึ่งเป็นไปตามe Lorentz-Einstein prediction อย่างชัดเจน
- การทดลองของ Hamar experiment — ไม่มี "การต้านทานเนื่องจากการไหลของอีเทอร์"
- การทดลองของ Kennedy-Thorndike — การยืดออกของเวลาเป็นไปตามการแปลงแบบลอเรนซ์
- การทดลองของ Rossi-Hall — ผลเชิงสัมพัทธภาพที่มีต่อครึ่งชีวิตของอนุภาคซึ่งเคลื่อนที่ด้วยความเร็วสูง
- การทดลองเพื่อทดสอบ emitter theory แสดงให้เห็นว่าอัตราเร็วแสงไม่ขึ้นอยู่กับอัตราเร็วของตัวเปล่งแสง
นอกจากนี้ เครื่องเร่งอนุภาคกำลังทำงานอยู่ทุกวันนี้ในหลายที่ของโลก และมันเร่งและวัดสมบัติของอนุภาคซึ่งเคลื่อนที่ใกล้ความเร็วแสงอยู่เสมอ ผลหลายอย่างที่พบในเครื่องเร่งอนุภาคสอดคล้องอย่างยิ่งกับทฤษฎีสัมพัทธภาพและขัดแย้งอย่างยิ่งกับ กลศาสตร์นิวตัน ก่อนหน้านั้น














































































![{\displaystyle T_{\left[j_{1}',j_{2}',...j_{q}'\right]}^{\left[i_{1}',i_{2}',...i_{p}'\right]}=\Lambda ^{i_{1}'}{}_{i_{1}}\Lambda ^{i_{2}'}{}_{i_{2}}...\Lambda ^{i_{p}'}{}_{i_{p}}\Lambda _{j_{1}'}{}^{j_{1}}\Lambda _{j_{2}'}{}^{j_{2}}...\Lambda _{j_{q}'}{}^{j_{q}}T_{\left[j_{1},j_{2},...j_{q}\right]}^{\left[i_{1},i_{2},...i_{p}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9eb24f5ef857f15d66b924e9616a97b60c32c5c6)





















![{\displaystyle [J_{x},J_{y},J_{z}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c02d555bb87d86f3e0e9a6954f618d72666120e)


![{\displaystyle [E_{x},E_{y},E_{z}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d5d56c325b3ea016fd9f240d68ee5ca7bd320c6)
![{\displaystyle [B_{x},B_{y},B_{z}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfa2a308707e4eeb53c3186078ea4203755f9533)




![{\displaystyle [D_{x},D_{y},D_{z}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65362b4a99f4b315d39b9157cb43ed4b90e7534c)
![{\displaystyle [H_{x},H_{y},H_{z}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fd791a7afef52415fed48a23b690db210eca18c)





