ความเร่ง
ลิงก์ข้ามภาษาในบทความนี้ มีไว้ให้ผู้อ่านและผู้ร่วมแก้ไขบทความศึกษาเพิ่มเติมโดยสะดวก เนื่องจากวิกิพีเดียภาษาไทยยังไม่มีบทความดังกล่าว กระนั้น ควรรีบสร้างเป็นบทความโดยเร็วที่สุด |
 | |
หากไม่คิดแรงต้านอากาศและเมื่อรวมเรื่องความเร็วสุดท้ายแล้ว ลูกบอลจะเคลื่อนที่ด้วยความเร็วที่เพิ่มขึ้น | |
| หน่วยการวัด (SI): | m/s2, m·s−2, m s−2 |
| สัญลักษณ์ที่มักจะใช้: | a |
ในฟิสิกส์เชิงคณิตศาสตร์ ความเร่ง (อังกฤษ: acceleration, สัญลักษณ์: a) คือ อัตราการเปลี่ยนแปลง (หรืออนุพันธ์เวลา) ของความเร็ว เป็นปริมาณเวกเตอร์ (ตามกฎสี่เหลี่ยมด้านขนาน) ที่มีหน่วยเป็น ความยาว/เวลา² ในหน่วยเอสไอกำหนดให้หน่วยเป็น เมตร/วินาที²
| กลศาสตร์ดั้งเดิม |
|---|
ยกตัวอย่างเช่น เมื่อรถเริ่มเคลื่อนที่จากจุดหยุดนิ่ง (ความเร็วเป็นศูนย์) เคลื่อนที่ไปตามแนวเส้นตรงด้วยความเร็วที่เพิ่มขึ้น ความเร่งจะมีทิศทางเดียวกันกับการเคลื่อนที่ ถ้ารถเปลี่ยนทิศทาง ความเร่งก็จะเปลี่ยนทิศทางตามไปด้วย เราจะเรียกการความเร่งที่ไปตามทิศทางของรถนี้ว่า "อัตราเร่งที่เป็นเส้นตรง (Linear Acceleration)" ซึ่งผู้โดยสารบนยานพาหนะบางคนอาจจะถูกดันลงไปกับเบาะ เมื่อเปลี่ยนทิศทางไป เราจะเรียกว่า "อัตราเร่งที่ไม่เป็นเส้นตรง (Non-Linear Acceleration)" ซึ่งผู้โดยสารบนยานพาหนะจะถูกแรงเหวี่ยง (Sideway Force) ออกไป

ถ้าความเร็วของรถลดลง ทิศทางของความเร่งจะตรงกันข้ามกับการเคลื่อนที่ (ความเร่งมีค่าติดลบ) หรือ ความหน่วง ซึ่งผู้โดยสารบนยานพาหนะจะถูกผลักไปด้านหน้าหากมีความหน่วง ตามหลักการทางคณิตศาสตร์แล้ว ความหน่วงจะไม่มีสมการเฉพาะแบบความเร่ง แต่จะเปลี่ยนไปตามความเร็วเท่านั้น
คำนิยามและสมบัติ
[แก้]ความเร่งเฉลี่ย
[แก้]ความเร่งเฉลี่ยของวัตถุใดวัตถุหนึ่งในช่วงเวลาใดเวลาหนึ่งคืออัตราการเปลี่ยนแปลงความเร็ว ต่อช่วงเวลา เขียนได้ว่า :
ความเร่ง ณ ขณะใดขณะหนึ่ง
[แก้]ความเร่ง ณ จุดใดจุดหนึ่ง คือลิมิตของความเร่งเฉลี่ยบนเวลากณิกนันต์ ในเชิงแคลคูลัส ความเร่ง ณ จุดใดจุดหนึ่งคืออนุพันธ์ของความเร็วตามเวลา :
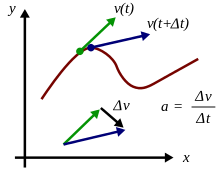
(ในที่นี้ หากการเคลื่อนที่เป็นเส้นตรง ปริมาณเวกเตอร์สามารถแทนที่ได้โดยสมการของปริมาณสเกลาร์)
จะเห็นได้ว่าอินทริกัลของฟังก์ชันความเร่ง a(t) คือฟังก์ชันของความเร็ว ν(t) ซึ่งก็คือพื้นที่ใต้กราฟความเร่ง/เวลา (กราฟ a-t) :

เมื่อความเร่งถูกนิยามไว้ว่าเป็นการเปลี่ยนแปลงความเร็ว (v) ต่อเวลา (t) และความเร็วถูกนิยามไว้ว่าเป็นการเปลี่ยนตำแหน่งของวัตถุ (x) ต่อเวลา (t) ความเร่งจะเขียนเป็นอนุพันธ์อันดับสองของ x ต่อ t ได้ว่า :
หน่วย
[แก้]ความเร่งมีมิติของความเร็ว (L/T) ส่วนด้วยเวลา
ในรูปแบบอื่นๆ
[แก้]วัตถุที่เคลื่อนที่เป็นแนวเส้นโค้ง (เช่น ดาวเทียมซึ่งโคจรอยู่รอบโลก) มีความเร่งซึ่งเปลี่ยนไปตามทิศทางการเคลื่อนที่ ซึ่งจะเป็นความเร่งสู่ศูนย์กลาง
ความเร่งสัมพัทธ์ เป็นความเร่งเมื่ออยู่ในสถานะตกแบบเสรี ซึ่งวัดโดยเครื่องวัดความเร่ง
สำหรับเรื่องกลศาสตร์ดั้งเดิม กฎข้อที่สองของนิวตันกล่าวไว้ว่า ในกรอบอ้างอิงเฉื่อยผลรวมของเวกเตอร์ของแรง F บนวัตถุมีค่าเท่ากับมวล m ของวัตถุนั้นคูณด้วยความเร่ง a ของวัตถุ :
เมื่อ :
F คือแรงทั้งหมดที่กระทำต่อวัตถุ
m คือมวลของวัตถุ
a เป็นความเร่งศูนย์กลางมวล
หากความเร็วเป็นค่าความเร็วที่ใกล้เคียงความเร็วแสง ตามหลักการทฤษฎีสัมพันธภาพพิเศษ มันจะมีขนาดใหญ่ขึ้นเรื่อยๆ
ความเร่งสู่ศูนย์กลางกับความสัมพันธ์แทนเจนต์
[แก้]
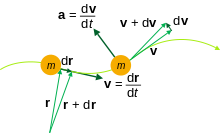
ความเร็วของการเคลื่อนที่บนเส้นโค้งของฟังก์ชันเวลาจะเขียนได้ว่า :
เมื่อ v(t) เท่ากับความเร็วทั้งหมด และ
คือหน่วยของเวกเตอร์แทนเจนต์ที่มุ่งไปยังทิศทางการเคลื่อนที่ในแต่ละช่วงเวลาต่าง ๆ

โดยจะอธิบายได้ว่า การเปลี่ยนแปลงของทั้งอัตราเร็ว v(t) และทิศทางของ ut สามารถแสดงถึงการเคลื่อนที่แบบเส้นโค้ง โดยใช้ความแตกต่างของกฎลูกโซ่ ผลลัพธ์ของฟังก์ชันเวลาทั้งสองฟังก์ชันจะได้ว่า :
เมื่อ ut เป็นหน่วย (สู่ศูนย์กลาง) เวกเตอร์แนวฉากต่อส่วนของเส้นโคจร (หรือแนวฉากมุขสำคัญ[1]) และ r คือเส้นเฉียดโค้ง (instantaneous radius of curvature) ซึ่งอิงวงกลมความโค้ง (osculating circle) ณ เวลา t ตัวประกอบของสมการพวกนี้เรียกว่า ความเร่งเชิงแทนเจนต์, ความเร่งปกติ และความเร่งของวัตถุในแนวรัศมี
กรณีพิเศษ
[แก้]ความเร่งสม่ำเสมอ
[แก้]ความเร่งสม่ำเสมอ หรือความเร่งคงที่เป็นการเคลื่อนที่ที่ซึ่งความเร็วของวัตถุนั้น ๆ เปลี่ยนแปลงอย่างสม่ำเสมอกับเวลา
ตัวอย่างที่ถูกใช้กับความเร่งสม่ำเสมอมากที่สุดก็คือการตกของวัตถุแบบเสรีภายใต้สนามแรงโน้มถ่วงซึ่งไม่คิดแรงต้านอากาศโดยใช้ค่าความโน้มถ่วงมาตรฐาน (หรือจะเรียกว่า ความเร่งเนื่องจากแรงโน้มถ่วง) ตามกฎการเคลื่อนที่ของนิวตันข้อที่สอง แรงที่ F กระทำต่อวัตถุ จะได้ว่า
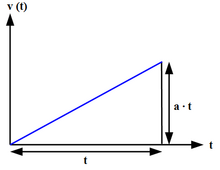
ตามสมการค่าความเร่งคงตัว จะมีสมการอยู่หนึ่งสมการซึ่งเกี่ยวข้องกับการกระจัด, ความเร็วต้นและความเร็วปลาย และความเร่งต่อเวลาที่ใช้ไป :
เมื่อ
- คือเวลาที่ใช้ไป
- คือการกระจัดเริ่มต้น
- คือระยะห่างระหว่างจุดเริ่มต้นและจุดสุดท้าย ณ เวลา t
- คือความเร็วต้น
- คือความเร็วปลาย ณ เวลา t
- คือความเร่งเฉลี่ย
ในบางกรณี การเคลื่อนที่แบบความเร็วคงตัวและอื่น ๆ จะเป็นไปตามสมการดังกล่าว ดังที่กาลิเลโอได้เขียนไว้ ผลรวมของการเคลื่อนที่แบบโพรเจกไทล์ ซึ่งจะมาช่วยอธิบาย (เส้นการเคลื่อนที่แบบโพรเจกไทล์ซึ่งจะเข้าสู่พื้นโลก)
การเคลื่อนที่แบบวงกลม
[แก้]การเคลื่อนที่แบบวงกลมคงที่ที่มีค่าอัตราเร็วตามเส้นโค้งเป็นตัวอย่างของผลความเร่งในขณะที่ขนาดของความเร็วมีค่าคงตัว ในกรณีนี้ เนื่องจากทิศทางการเคลื่อนที่ของวัตถุมีการเปลี่ยนแปลงอย่างสม่ำเสมอ โดยจะทำมุม กับวงกลม เส้นเวกเตอร์ความเร็วของวัตถุจะเปลี่ยนแปลงไป แต่อัตราเร็วจะไม่เปลี่ยนไป ความเร่งนี้เรียกว่าความเร่งเชิงรัศมี เนื่องจากมีทิศทางไปข้างหน้าตามจุดศูนย์กลาง :
เมื่อ v คือเส้นอัตราเร็วของวัตถุตามส่วนของเส้นโค้ง ซึ่งสมมูลกับ เวกเตอร์ความเร่งเชิงรัศมี a ซึ่งจะหาจากความเร็วเชิงมุม :
เมื่อ r คือเวกเตอร์จากจุดศูนย์กลางและมีขนาดเท่ากับรัศมี ส่วนค่าลบแสดงถึงเวกเตอร์ความเร่งซึ่งเคลื่อนที่ไปตามจุดศุนย์กลาง (ตรงข้ามกับรัศมี)
ความเร่งและแรงรวมที่กระทำต่อวัตถุในการเคลื่อนที่แบบวงกลมคงที่มีทิศทางไปข้างหน้าจากจุดศูนย์กลางของวงกลม ซึ่งก็คือแรงสู่ศูนย์กลาง และยังมีแรงหนีศูนย์กลาง ซึ่งจะกระทำต่อวัตถุ ซึ่งจริง ๆ แล้ว แรงหนีศูนย์กลางนั้นเป็นเพียงแรงเทียมจากกรอบอ้างอิงหมุนของวัตถุ จากโมเมนตัมเชิงมุมของวัตถุ
หากเป็นการเคลื่อนที่วงกลมไม่คงที่ (อัตราเร็วระหว่างส่วนของเส้นโค้งเปลี่ยนไป) ความเร่งตามขวางจะเปลี่ยนไปตามอัตราการเปลี่ยนแปลงของอัตราเร็วเชิงมุมตามเส้นโค้งตามรัศมีของวงกลม :
ความเร่งตามขวาง (หรือความเร่งซึ่งทำมุม tanθ) มีทิศทางทำมุมกับเวกเตอร์รัศมี ใช้สัญลักษณ์ความเร่งเชิงมุม ()
ความเร่งกับทฤษฎีสัมพันธภาพ
[แก้]ทฤษฎีสัมพันธภาพพิเศษ
[แก้]บทความหลัก : ทฤษฎีสัมพันธภาพพิเศษ
ทฤษฎีสัมพันธภาพพิเศษอธิบายถึง "พฤติกรรม" ของวัตถุที่กำลังเคลื่อนที่สัมพันธ์กับวัตถุอื่นในความเร็วใกล้ความเร็วแสงในสถานะสุญญากาศไว้ กลศาสตร์ดั้งเดิมได้อธิบายไว้ใกล้เคียงความเป็นจริงมาก แต่หากเป็นความเร็วที่เพิ่มขึ้นเป็นความเร็วแสง ความเร่งจะไม่เป็นไปตามสมการธรรมดาอีก
หากความเร็วของวัตถุใดวัตถุหนึ่งมีค่าเข้าใกล้ความเร็วแสง ความเร่งจะเพิ่มขึ้นในขณะที่แรงลดลง และจะมีขนาดเป็นกณิกนันต์ หากวัตถุมีความเร็วเท่ากับแสง
หากเป็นวัตถุที่มีมวล ความเร็วจะเข้าใกล้ความเร็วแสงอย่างเป็นเส้นกำกับ (Asymptote) (ลู่เข้าหากัน แต่ไม่บรรจบกัน)
ทฤษฎีสัมพันธภาพทั่วไป
[แก้]บทความหลัก : ทฤษฎีสัมพันธภาพทั่วไป
จากการเคลื่อนที่ของวัตถุที่เป็นที่รู้จักกัน จะสามารถแยกได้ว่าแรงที่ถูกสังเกตอยู่ (Observed Force) นั้นมาจากความโน้มถ่วง หรือจากความเร่ง ความโน้มถ่วงและความเร่งเฉื่อยจะทำให้เวลาเดินช้าลง อัลเบิร์ต ไอน์สไตน์ เรียกปรากฏการณ์นี้ว่าหลักแห่งความสมมูล (Equivalence Principle) และบอกว่าผู้สังเกตการณ์จะไม่รู้สึกถึงแรง รวมไปถึงแรงโน้มถ่วง แค่เพียงสรุปได้ว่าวัตถุนั้นไม่มีความเร่ง[2]
การแปลงหน่วย
[แก้]บทความหลัก : เมตรต่อวินาทีกำลังสอง
| ค่าฐาน | (กาลิเลโอ, หรือเซนติเมตรต่อวินาที2) | (ฟุตต่อวินาที2) | (เมตร/วินาที2) | (แรงโน้มถ่วง (เมื่อตกแบบเสรี), g0) |
|---|---|---|---|---|
| 1 กาลิเลโอ, หรือเซนติเมตรต่อวินาที2 | 1 | 0.0328084 | 0.01 | 0.00101972 |
| 1 ฟุต/วินาที2 | 30.4800 | 1 | 0.304800 | 0.0310810 |
| 1 เมตร/วินาที2 | 100 | 3.28084 | 1 | 0.101972 |
| 1 g0 | 980.665 | 32.1740 | 9.80665 | 1 |
ดูเพิ่ม
[แก้]- ความเฉื่อย
- เวกเตอร์สี่มิติ
- ความเร่งเนื่องจากแรงโน้มถ่วง
- อันดับของขนาด (ความเร่ง)
- ช็อก (กลศาสตร์)
- แรงจำเพาะ
อ้างอิง
[แก้]- ↑ https://dict.longdo.com/search/principal%20normal
- ↑ Brian Greene, The Fabric of the Cosmos: Space, Time, and the Texture of Reality, page 67. Vintage ISBN 0-375-72720-5















![{\displaystyle {\displaystyle {\mathbf {v} ^{2}}(t)={\mathbf {v} _{0}}^{2}+2\mathbf {a\times } [\mathbf {s} (t)-\mathbf {s} _{0}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c42e9d21d0d8fbed2e2f7df4cc94bc290f7e8ec)














