การอุปนัยเชิงคณิตศาสตร์

ระวังสับสนกับ การอนุมานแบบอุปนัย หรือ การให้เหตุผลแบบอุปนัย

การอุปนัยเชิงคณิตศาสตร์สามารถถูกแสดงให้เห็นอย่างอรูปนัยได้ด้วยการเทียบกับผลกระทบลูกโซ่แบบโดมิโนที่ล้มทับกัน

การอุปนัยเชิงคณิตศาสตร์ (อังกฤษ: Mathematical induction) เป็นเทคนิคการพิสูจน์เชิงคณิตศาสตร์ที่ใช้เพื่อพิสูจน์ว่าข้อความ P(n) เป็นจริงสำหรับจำนวนธรรมชาติทุกจำนวน n = 0, 1, 2, 3, . . . ; แปลว่าข้อความทั้งสิ้นเป็นลำดับของกรณี P(0), P(1), P(2), P(3), . . . . จำนวนมากไม่สิ้นสุด เราสามารถใช้คำอุปมาเพื่ออธิบายเทคนิคนี้ได้อย่างอรูปนัยด้วยการเทียบกับโดมิโนที่ล้มตาม ๆ กันหรือการปีนบันได:

"การอุปนัยเชิงคณิตศาสตร์พิสูจน์ว่าเราสามารถปีนบันไดสูงเท่าไหร่ก็ได้ พิสูจน์โดยการปีนขึ้นขั้นแรก (ฐานของบันได) และจากนั้นก็สามารถปีนขึ้นขั้นต่อไปจากขั้นไหนก็ได้"

— Concrete Mathematics, ริมกระดาษหน้า 3

การพิสูจน์ด้วยการอุปนัย (proof by induction) ประกอบไปด้วยกรณีสองกรณี กรณีแรกคือ กรณีฐาน (base case หรือ basis) เป็นการพิสูจน์สำหรับข้อความที่ n = 0 โดยไม่ต้องรู้อะไรเกี่ยวกับกรณีอื่น ๆ เลย กรณีที่สองคือ ขั้นตอนอุปนัย (induction step) เป็นการพิสูจน์ว่าถ้าข้อความเป็นจริงสำหรับ n = k ใด ๆ แล้ว มันก็ต้องเป็นจริงสำหรับกรณี n = k + 1 ถัด ๆ ไปด้วย ขั้นตอนสองขั้นตอนนี้แสดงให้เห็นว่าข้อความนั้นเป็นจริงสำหรับจำนวนธรรมชาติ n ทุกจำนวน กรณีฐานไม่จำเป็นต้องเริ่มด้วย n = 0 แต่มักจะเริ่มด้วย n = 1 และก็เป็นไปได้ที่จะใช้จำนวนธรรมชาติ n = N คงที่ใด ๆ เพื่อแสดงให้เห็นว่าข้อความเป็นจริงสำหรับจำนวนธรรมชาติ n ≥ N ทุกตัว

วิธีการนี้สามารถนำมาขยายใช้เพื่อพิสูจน์ข้อความเกี่ยวกับโครงสร้างรากฐานดี (well-founded) ที่ทั่วไปมากขึ้นเช่นต้นไม้ (tree (set theory)) การวางนัยทั่วไปนี้ซึ่งมีชื่อว่าการอุปนัยเชิงโครงสร้าง (structural induction) ถูกใช้ในคณิตตรรกศาสตร์และวิทยาการคอมพิวเตอร์ การอุปนัยเชิงคณิตศาสตร์ในความหมายแบบขยายมีความใกล้เคียงกับการเรียกซ้ำ การอุปนัยเชิงคณิตศาสตร์เป็นกฏการอนุมาน (rule of inference) ที่ถูกใช้ในการพิสูจน์เชิงรูปนัย (formal proof) และในบางรูปแบบก็เป็นรากฐานของการพิสูจน์ความถูกต้องของโปรแกรมคอมพิวเตอร์ (formal verification) ทั้งหมด

แม้ชื่อจะคล้ายกันแต่ไม่ควรสับสนการอุปนัยเชิงคณิตศาสตร์กับการให้เหตุผลแบบอุปนัยที่ใช้ในปรัชญา (ดูปัญหาของการอุปนัย (Problem of induction)) วิธีการทางคณิตศาสตร์วิธีนี้ตรวจสอบกรณีจำนวนมากเป็นอนันต์เพื่อพิสูจน์ข้อความทั่วไปข้อหนึ่ง แต่ทำเช่นนั้นด้วยอนุกรมของการให้เหตุผลแบบนิรนัยจำนวนจำกัดซึ่งใช้ตัวแปร n แทนค่าจำนวนได้มากเป็นอนันต์

ประวัติ

ในปี 370 ก่อนคริสต์ศักราช พาร์เมนิเดสของเพลโตมีตัวอย่างแรก ๆ ของการพิสูจน์แบบอุปนัยโดยปริยาย การนำการอุปนัยเชิงคณิตศาสตร์มาใช้อย่างชัดเจนเป็นครั้งแรกที่สุดสามารถพบได้ในการพิสูจน์ของยุคลิดที่บอกว่ามีจำนวนเฉพาะมากเป็นอนันต์ เทคนิคการทำซ้ำซึ่งตรงข้ามกันใช้การนับลงแทนการนับเพิ่มขึ้นที่ละหนึ่งและสามารถพบได้ในปฏิทรรศน์กองทราย (sorites paradox) ซึ่งมีการอ้างเหตุผลว่าหากทราย 1,000,000 เม็ดก่อตัวเป็นกองทรายและการเอาทรายออกเม็ดหนึ่งกองนั้นก็ยังถูกนับได้ว่าเป็นกองทรายแล้ว ทรายเพียงเม็ดเดียว (หรือไม่มีสักเม็ดเลย) ก็เป็นกองทรายเช่นเดิม

การพิสูจน์โดยปริยายด้วยการอุปนัยเชิงคณิตศาสตร์แรก ๆ ในประเทศอินเดียปรากฏอยู่ใน "จักรวาลวิธี" (Chakravala method) ของภาสคาราที่ 2 (Bhāskara II) และใน อัลฟะครี (al-Fakhri) ซึ่งถูกเขียนขึ้นในประมาณปี ค.ศ. 1000 โดยอัลกะระญี (al-Karaji) ซึ่งเขานำมาประยุกต์ใช้กับอนุกรมเลขคณิตเพื่อพิสูจน์ทฤษฎีบททวินามและคุณสมบัติของสามเหลี่ยมปัสกาล

เกร์โซนิเดส (Gersonides) (ค.ศ. 1288-1344) เป็นผู้ใช้การอุปนัยอย่างเคร่งครัดเป็นครั้งแรก แบลซ ปัสกาล บัญญัติหลักของการอุปนัยอย่างชัดแจ้งเป็นครั้งแรกใน Traité du triangle arithmétique (ค.ศ. 1665) ชาวฝรั่งเศสอีกคนหนึ่งชื่อ ปีแยร์ เดอ แฟร์มา นำหลักการที่เกี่ยวข้องมาใช้: การพิสูจน์อ้อมด้วยการลดหลั่นอนันต์ (Proof by infinite descent)

สมมติฐานการอุปนัยนี้ยังถูกนำมาใช้โดย ยาคอบ แบร์นูลลี (Jakob Bernoulli) และก็กลายเป็นที่รู้จักตั้งแต่นั้นมา การปฏิบัติต่อหลักการนี้อย่างรูปนัยแบบสมัยใหม่มีขึ้นในคริสตศตวรรษที่ 19 โดย จอร์จ บูล ออกัสตัส เดอ มอร์แกน (Augustus de Morgan), ชารลส์ แซนเดอรส์ เพิร์ซ (Charles Sanders Peirce), จูเซ็ปเป เปอาโน (Giuseppe Peano) และ ริชาร์ด เดเดคินด์ (Richard Dedekind)

คำบรรยาย

รูปแบบการอุปนัยเชิงคณิตศาสตร์ที่ง่ายและพบเจอได้มากที่สุดอนุมานว่าข้อความใด ๆ ที่มีการใช้จำนวนธรรมชาติ $n$ (นั้นคือจำนวนเต็ม $n\geq 0$ หรือ 1) เป็นจริงสำหรับค่า $n$ ใด ๆ การพิสูจน์ประกอบด้วยสองขั้นตอนคือ:

1. กรณีฐาน หรือ กรณีต้น: พิสูจน์ว่าข้อความเป็นจริงสำหรับค่า 0 หรือ 1
2. ขั้นตอนอุปนัย หรือ กรณีขั้นตอน: พิสูจน์ว่าหากข้อความเป็นจริงสำหรับค่า $n$ ทุกค่า ข้อความจะเป็นจริงสำหรับ $n+1$ ด้วย หรือพูดอีกแบบคือให้สมมุติว่าข้อความเป็นจริงสำหรับจำนวนธรรมชาติ n ใด ๆ และพิสูจน์ว่าข้อความนั้นเป็นจริงสำหรับค่า $n+1$

สมมติฐานในขั้นตอนการอุปนัยที่กล่าวว่าข้อความเป็นจริงกับค่า $n$ ค่าหนึ่งเรียกว่า สมมติฐานอุปนัย ต้องมีการสมุมติสมมติฐานอุปนัยสำหรับค่า $n$ และใช้สมมติฐานนี้เพื่อพิสูจน์ว่าข้อความนั้นเป็นจริงสำหรับ $n+1$ เพื่อพิสูจน์ขั้นตอนอุปนัย

ผู้ที่นิยมนิยามของจำนวนธรรมชาติซึ่งเริ่มจาก 0 จะใช้จำนวนนี้ในกรณีฐาน ผู้ที่นิยมนิยามของจำนวนธรรมชาติซึ่งเริ่มจาก 1 จะใช้จำนวนนี้แทน

ตัวอย่าง

ผลบวกของจำนวนธรรมชาติที่ต่อเนื่องตามลำดับ

การอุปนัยเชิงคณิตศาสตร์สามารถนำมาใช้เพื่อพิสูจน์ข้อความ P(n) ดังต่อไปนี้สำหรับจำนวนธรรมชาติ n ทุกจำนวนได้

$P(n)\!:\ \ 0+1+2+\cdots +n\,=\,{\frac {n(n+1)}{2}}.$

นี่เป็นสูตรทั่วไปสำหรับผลบวกของจำนวนธรรมชาติที่น้อยกว่าหรือเท่ากับจำนวนที่กำหนด ซึ่งเป็นอนุกรมของข้อความจำนวนมากเป็นอนันต์โดยพฤตินัย: $0={\tfrac {(0)(0+1)}{2}}$, $0+1={\tfrac {(1)(1+1)}{2}}$, $0+1+2={\tfrac {(2)(2+1)}{2}}$, ฯลฯ

ประพจน์ สำหรับจำนวน $n\in \mathbb {N}$ ใด ๆ, $0+1+2+\cdots +n={\tfrac {n(n+1)}{2}}.$

การพิสูจน์ ให้ P(n) เป็นข้อความ $0+1+2+\cdots +n={\tfrac {n(n+1)}{2}}.$ และเราพิสูจน์โดยการอุปนัยกับ n

กรณีฐาน: แสกงให้เห็นว่าข้อความนี้เป็นจริงกับจำนวนธรรมชาติที่น้อยทีสุด n = 0.

P(0) เป็นจริงอย่างชัดเจน: $0={\tfrac {0(0+1)}{2}}\,.$

ขั้นตอนอุปนัย: แสดงให้เห็นว่าสำหรับค่า k ≥ 0 ใด ๆ หาก P(k) เป็นจริงแล้ว P(k+1) จะเป็นจริงด้วย

สมมุติสมมติฐานอุปนัยว่าสำหรับค่า k ค่าหนึ่ง กรณีที่ n = k เป็นจริง หมายความว่า P(k) เป็นจริงด้วย:

$0+1+\cdots +k\ =\ {\frac {k(k{+}1)}{2}}.$

ดังนั้น:

$(0+1+2+\cdots +k)+(k{+}1)\ =\ {\frac {k(k{+}1)}{2}}+(k{+}1).$

ฝั่งขวาสามารถทำให้ง่ายด้วยวิธีการทางพีชคณิตเป็น:

${\begin{aligned}{\frac {k(k{+}1)}{2}}+(k{+}1)&\ =\ {\frac {k(k{+}1)+2(k{+}1)}{2}}\\&\ =\ {\frac {(k{+}1)(k{+}2)}{2}}\\&\ =\ {\frac {(k{+}1)((k{+}1)+1)}{2}}.\end{aligned}}$

จับฝั่งซ้ายและฝั่งขวาเข้าสมการ เรานิรนัยได้ว่า:

$0+1+2+\cdots +k+(k{+}1)\ =\ {\frac {(k{+}1)((k{+}1)+1)}{2}}.$

นั่นคือข้อความว่า P(k+1) เป็นจริงด้วย เป็นการแสดงขั้นตอนอุปนัย

ข้อสรุป: เนื่องจากทั้งกรณีฐานและขั้นตอนอุปนัยถูกพิสูจน์แล้วว่าเป็นจริง ข้อความ P(n) จึงเป็นจริงสำหรับจำนวนธรรมชาติ n ทุกจำนวนด้วยการอุปนัยเชิงคณิตศาสตร์ ∎

อสมการตรีโกณมิติ

อสมการมักถูกพิสูจน์ด้วยการอุปนัย เราจะพิสูจน์ว่า $|\!\sin nx|\leq n|\!\sin x|$ สำหรับจำนวนจริง $x$ และจำนวนธรรมชาติ $n$ ใด ๆ

แวบแรกที่มอง รูปแบบของสมการที่ทั่วไปกว่า $|\!\sin nx|\leq n\,|\!\sin x|$ สำหรับจำนวนจริง $n,x$ ใด ๆ อาจดูเหมือนว่าสามารถพิสูจน์ได้โดยไม่ต้องอุปนัย แต่กรณีที่ ${\textstyle n={\frac {1}{2}},\,x=\pi }$ แสดงให้เห็นว่าข้อความนี้สามารถเป็นเท็จได้สำหรับค่า $n$ ที่ไม่ใช่จำนวนเต็ม ทำให้เราต้องพิจารณาข้อความสำหรับจำนวน $n$ ที่เป็นจำนวนธรรมชาติโดยเฉพาะและการอุปนัยเป็นเครื่องมือที่พร้อมนำมาใช้ที่สุด

ประพจน์. สำหรับค่า $x\in \mathbb {R} ,n\in \mathbb {N}$ ใด ๆ, $|\!\sin nx|\leq n\,|\!\sin x|$.

การพิสูจน์ กำหนดจำนวนจริง $x$ ค่าใด ๆ ค่าหนึ่ง, และให้ $P(n)$ เป็นข้อความ $|\!\sin nx|\leq n\,|\!\sin x|$. และเราพิสูจน์โดยการอุปนัยกับ $n$.

กรณีฐาน: การคำนวณ $|\!\sin 0x|=0\leq 0=0\,|\!\sin x|$ พิสูจน์ว่า $P(0)$ เป็นจริง.

ขั้นตอนอุปนัย: เราจะแสดงว่า $P(k)\implies P(k{+}1)$ สำหรับจำนวนธรรมชาติ $k$ ใด ๆ. สมมุติสมมติฐานอุปนัยว่าสำหรับค่า $n=k\geq 0$ กรณีของ $P(k)$ จะเป็นจริง เรานิรนัยโดยใช้สูตรผลบวกของมุมและอสมการอิงรูปสามเหลี่ยมได้:

${\begin{array}{rcll}|\sin(k{+}1)x|&=&|\sin kx\,\cos x+\sin x\,\cos kx\,|&{\text{(ผลบวกของมุม)}}\\&\leq &|\!\sin kx\,\cos x|+|\!\sin x\,\cos kx|&{\text{(อสมการอิงรูปสามเหลี่ยม)}}\\&=&|\!\sin kx|\,|\!\cos x|+|\!\sin x|\,|\!\cos kx|&\\&\leq &|\!\sin kx|+|\!\sin x|&(\,|\!\cos t|\leq 1)\\&\leq &k\,|\!\sin x|+|\!\sin x|&{\text{(สมมติฐานอุปนัย}})\\&\ =\ &(k{+}1)\,|\!\sin x|.&\end{array}}$

อสมการระหว่างฝั่งซ้ายและฝั่งขวาแสดงให้เห็นว่า $P(k{+}1)$ เป็นจริง ขั้นตอนอุปนัยจึงเสร็จสมบูรณ์

ข้อสรุป: ประพจน์ $P(n)$ เป็นจริงสำหรับเลขจำนวนธรรมชาติ $n$ ทุกค่า ∎

รูปแปรผัน

ในทางปฏิบัติ การพิสูจน์โดยการอุปนัยมักมีแบบแผนที่ต่างกันซึ่งขึ้นอยู่กับลักษณะของคุณสมบัติที่เราต้องการจะพิสูจน์ รูปแปรผันของการอุปนัยทุกรูปแบบเป็นกรณีพิเศษของการอุปนัยเชิงอนันต์ ดูด้านล่าง

ฐานของการอุปนัยนอกเหนือจาก 0 หรือ 1

หากเราไม่ประสงค์จะพิสูจน์ข้อความหนึ่งสำหรับจำนวนธรรมชาติทุกจำนวน แต่ต้องการพิสูจน์เพียงสำหรับจำนวน n ทุกจำนวนที่มีค่ามากกว่าหรือเท่ากับค่า b เท่านั้นแล้ว การพิสูจน์ด้วยการอุปนัยจะประกอบด้วย:

1. การแสดงให้เห็นว่าข้อความเป็นจริงเมื่อ $n=b$
2. การแสดงให้เห็นว่าหากข้อความเป็นจริงสำหรับค่า ${\textstyle n\geq b}$ ค่าหนึ่งแล้ว ข้อความเดียวกันนี้ก็จะเป็นจริงสำหรับค่า $n+1$ ด้วย

เราสามารถนำวิธีนี้มาใช้เพื่อแสดงให้เห็นว่า ${\textstyle 2^{n}\geq n+5}$ สำหรับ $n\geq 3$

เราสามารถพิสูจน์ได้ว่าข้อความ $P(n)$ ข้อความหนึ่งเป็นจริงสำหรับค่า $n\geq 1$ หรือแม้แต่สำหรับค่า $n\geq -5$ การอุปนัยเชิงคณิตศาสตร์รูปแบบนี้ความจริงแล้วเป็นกรณีพิเศษของรูปแบบก่อนหน้าเพราะหากข้อความที่ถูกพิสูจน์คือ $P(n)$ แล้ว การพิสูจน์ด้วยกฎสองข้อนี้ก็เท่ากับการพิสูจน์ข้อความ $P(n+b)$ สำหรับจำนวนธรรมชาติ $n$ ทุกจำนวนโดยมีกรณีฐานอุปนัยกับค่า $0$

ตัวอย่าง: การใช้เหรียญบาทต่าง ๆ เพื่อให้รวมได้จำนวนเงินจำนวนหนึ่ง

สมมติว่าเรามีเหรียญสี่บาทและเหรียญห้าบาทจำนวนไม่จำกัด เราสามารถใช้การอุปนัยเพื่อพิสูจน์ได้ว่าจำนวนเต็มของเงินบาทใด ๆ ที่มากกว่าหรือเท่ากับ $12$ สามารถใช้เหรียญสี่บาทและห้าบาทมารวมกันได้จำนวนนั้น ให้ $S(k)$ เป็นข้อความว่า "จำนวนเงิน $k$ บาทสามารถรวมมาจากเหรียญสี่บาทและเหรียญห้าบาท" การพิสูจน์ว่า $S(k)$ เป็นจริงสำหรับค่า $k\geq 12$ ทุกค่าสามารถทำได้ด้วยการอุปนัยกับ $k$ ดังนี้:

กรณีฐาน: การแสดงให้เห็นว่า $S(k)$ เป็นจริงสำหรับ $k=12$ ง่ายมาก เพียงแค่มีเหรียญสี่บาทสามเหรียญ

ขั้นตอนอุปนัย: กำหนดให้ $S(k)$ เป็นจริงสำหรับค่า $k\geq 12$ ค่าหนึ่ง (สมมติฐานอุปนัย) พิสูจน์ว่า $S(k+1)$ เป็นจริงด้วย:

สมมติให้ $S(k)$ เป็นจริงสำหรับค่า $k\geq 12$ ใด ๆ หากมีคำตอบสำหรับจำนวน $k$ บาทที่อย่างน้อยต้องมีเหรียญสี่บาทอยู่หนึ่งเหรียญ เพียงแค่เปลี่ยนเหรียญสี่บาทเป็นเหรียญห้าบาทสักหนึ่งเหรียญก็จะได้จำนวนเงิน $k+1$ บาท หรือหากในคำตอบมีแต่เหรียญห้าบาท $k$ จำต้องเป็นจำนวนที่เป็นผลคูณของ 5 เพราะฉะนั้นต้องมีค่าเท่ากับ 15 เป็นอย่างน้อย เราจึงสามารถแทนเหรียญห้าบาททั้งสามเหรียญเป็นเหรียญสี่บาทสี่เหรียญเพื่อให้ได้จำนวนเงิน $k+1$ บาท ในกรณีแต่ละกรณีข้อความ $S(k+1)$ เป็นจริง

เพราะฉะนั้น $S(k)$ เป็นจริงสำหรับค่า $k\geq 12$ ทุกค่าด้วยหลักของการอุปนัย และการพิสูจน์จึงสมบูรณ์

แม้ $S(k)$ จะเป็นจริงสำหรับค่า $k\in \{4,5,8,9,10\}$ ในตัวอย่างนี้ด้วย เราไม่สามารถดัดแปลงค่าต่ำสุด $12$ ให้น้อยไปกว่านี้ได้อีกเป็นค่า $m$ ในการพิสูจน์ข้างบน สำหรับ $m=11$ กรณีฐานเป็นเท็จ สำหรับ $m=10$ กรณีที่สองในขั้นตอนอุปนัยจะใช้ไม่ได้ (การแทนเหรียญห้าบาทเป็นเหรียญสี่บาททำไม่ได้) ส่วนสำหรับค่า $m$ ที่น้อยกว่านี้ก็ไม่จำเป็นต้องเอ่ยถึงเลย

การอนุมานกับตัวนับมากกว่าหนึ่งตัว

บางครั้งก็เป็นการดีกว่าที่จะใช้จำนวนธรรมชาติสองจำนวน n กับ m เพื่อพิสูจน์ข้อความข้อหนึ่งด้วยการทำกระบวนการอุปนัยซ้ำ นั่นคือการพิสูจน์กรณีฐานและขั้นตอนอุปนัยสำหรับ n และก็พิสูจน์สำหรับ m ด้วย ดูตัวอย่างได้ใน การพิสูจน์สมบัติการสลับที่ (Proofs involving the addition of natural numbers) ซึ่งประกอบการบวกจำนวนธรรมชาติ การอ้างเหตุผลที่ซับซ้อนกว่านี้อาจมีตัวนับได้ถึงสามตัวหรือมากกว่า

การลดหลั่นอนันต์

บทความหลัก: การลดหลั่นอนันต์

วิธีการการลดหลั่นอนันต์ (อังกฤษ: Infinite descent) เป็นรูปแปรผันของการอุปนัยเชิงคณิตศาสตร์ที่ ปีแยร์ เดอ แฟร์มา ใช้เพื่อแสดงให้เห็นว่าข้อความ Q(n) ข้อหนึ่งเป็นเท็จสำหรับจำนวนธรรมชาติ n ทุกจำนวน รูปแบบดั้งเดิมประกอบไปด้วยการแสดงว่าถ้า Q(n) เป็นจริงสำหรับจำนวนธรรมชาติ n ค่าหนึ่งก็จะเป็นจริงสำหรับค่า m ที่น้อยกว่าโดยแท้ แต่เพราะจำนวนธรรมชาติที่ลดหลั่นอย่างไม่สิ้นสุดไม่มีอยู่จริงจึงทำให้สถานการณ์นี้เป็นไปไม่ได้ และดังนั้นจึงเป็นการแสดง (โดยข้อขัดแย้ง) ว่า Q(n) ไม่สามารถเป็นจริงได้สำหรับค่า n ใด ๆ

เราสามารถพิสูจน์ยืนยันความสมเหตุสมผลของวิธีการนี้ได้จากหลักปกติของการอุปนัยเชิงคณิตศาสตร์ ด้วยการใช้การอุปนัยเชิงคณิตศาสตร์กับข้อความ P(n) ซึ่งถูกนิยามไว้ว่า "Q(m) เป็นเท็จสำหรับจำนวนธรรมชาติ m ทุกค่าที่น้อยกว่าหรือเท่ากับ n" จึงแสดงว่า P(n) เป็นจริงสำหรับ n ทุกค่า ซึ่งแปลว่า Q(n) เป็นเท็จสำหรับจำนวนธรรมชาติ n ทุกจำนวน

การอุปนัยตัวเติมหน้า

รูปแบบของการพิสูจน์โดยการอุปนัยเชิงคณิตศาสตร์ที่พบได้ทั่วไปที่สุดมีความจำเป็นให้พิสูจน์ในขั้นตอนอุปนัยว่า

$\forall k(P(k)\to P(k+1))$

ซึ่งต่อจากนั้นหลักการอุปนัยจะ "ทำโดยอัตโนมัติ" (automate) การใช้ขั้นตอนนี้จำนวน n ครั้งเพื่อไปจาก P(0) สู่ P(n) นี่เรียกได้ว่าเป็น "การอุปนัยตัวนำหน้า" เพราะในแต่ละขั้นตอนก็เป็นการพิสูจน์บางสิ่งเกี่ยวกับเลขตัวหนึ่งจากบางสิ่งที่เกี่ยวกับเลขที่นำหน้าเลขตัวนั้น

สิ่งหนึ่งซึ่งได้รับความสนใจในเรื่องความซับซ้อนในการคำนวณคือ "การอุปนัยตัวเติมหน้า" (อังกฤษ: prefix induction) ซึ่งเป็นการพิสูจน์ข้อความดังต่อไปนี้ในขั้นตอนอุปนัย

$\forall k(P(k)\to P(2k)\land P(2k+1))$

หรือซึ่งสมมูลกัน

$\forall k\left(P\left(\left\lfloor {\frac {k}{2}}\right\rfloor \right)\to P(k)\right)$

แล้วหลักการอุปนัยจึง "ทำโดยอัตโนมัติ" การใช้การอนุมานนี้จำนวน log n ครั้งเพื่อไปจาก P(0) สู่ P(n) ที่เรียกว่า "การอุปนัยตัวเติมหน้า" เพราะแต่ละขั้นตอนเป็นการพิสจน์บางสิ่งเกี่ยวกับเลขตัวหนึ่งจากบางสิ่งที่เกี่ยวกับ "ตัวเติมหน้า" (prefix) ของเลขตัวนั้นซึ่งถูกสร้างขึ้นจากการตัดปลายบิต (bit) ส่วนต่ำของการแทนเลขแบบฐานสอง และยังสามารถมองเป็นการประยุกต์การอุปนัยแบบดั้งเดิมกับความยาวของการแทนแบบฐานสอง

หากการอุปนัยตัวนำหน้าถูกตีความทางคำนวณว่าเป็นวงวน (loop) n ขั้นตอนแล้ว การอุปนัยตัวเติมหน้าก็จะสมนัยกับวงวน log n ขั้นตอน เพราะฉะนั้นการพิสูจน์โดยใช้การอุปนัยตัวเติมหน้าจึง "สรรค์สร้างอย่างเป็นไปได้" (feasibly constructive) มากกว่าการพิสูจน์ซึ่งใช้การอุปนัยตัวนำหน้า

การอุปนัยตัวนำหน้าสามารถจำลองการอุปนัยตัวเติมหน้ากับข้อความเดียวกันได้อย่างชัด การอุปนัยตัวเติมหน้าสามารถจำลองการอุปนัยตัวนำหน้าได้แต่ต้องแลกมาด้วยการทำให้วากยสัมพันธ์ของข้อความซับซ้อนขึ้น (เพิ่มตัวบ่งปริมาณทั้งหมดซึ่งมีขอบเขต) ผลลัพธ์ซึ่งแสดงความสัมพันธ์ของการอุปนัยตัวเติมหน้ากับการคำนวณซึ่งใช้เวลาพหูพจน์ (polynomial time) จึงขึ้นอยู่กับการเอาตัวบ่งปริมาณซึ่งไม่มีขอบเขตออกไปทั้งหมดและการจำกัดจำนวนการสับเปลี่ยนระหว่างตัวบ่งปริมาณทั้งหมดซึ่งมีขอบเขตกับตัวบ่งปริมาณบางตัวที่อนุญาตให้ทำในข้อความ

การอุปนัยอย่างเข้ม

รูปแปรผันอีกรูปหนึ่งเรียกว่า การอุปนับอย่างเข้ม (อังกฤษ: Complete induction หรือ Strong induction) (ตรงข้ามกันคือรูปแบบของการอุปนัยขั้นพื้นฐานซึ่งบางครั้งก็เรียกว่า การอุปนัยอย่างอ่อน (weak induction)) ทำให้ขั้นตอนอุปนัยพิสูจน์ได้ง่ายขั้นด้วยการใช้สมมติฐานที่แรงขึ้น: เราพิสูจน์ข้อความ P(m + 1) ภายใต้สมมติฐานว่า P(n) เป็นจริงสำหรับจำนวนธรรมชาติ n ทุกจำนวนซึ่งน้อยกว่า m + 1 ในทางตรงกันข้ามรูปแบบพื้นฐานสมมุติเพียง P(m) "การอุปนัยอย่างเข้ม" เป็นชื่อที่ไม่ได้หมายความว่าวิธีนี้สามารถพิสูจน์ได้เยอะกว่า "การอุปนัยแบบอ่อน" แต่หมายถึงเพียงสมมติฐานที่ถูกใช้ในขั้นตอนอุปนัยที่แรงขึ้น

ความจริงแล้วเราสามารถแสดงให้เห็นว่าทั้งสองวิธีนั้นสมมูลกันตามที่อธิบายไว้ด้านล่าง กรณีฐาน P(0) ยังจำเป็นต้องถูกพิสูจน์และอาจจำเป็นต้องพิสูจน์กรณีฐานเพิ่มเติมด้วยเช่น P(1) ในการอุปนัยอย่างเข้มก่อนที่การอ้างเหตุผลแบบทั่วไปจะใช้ได้ อย่างเช่นตัวอย่างของจำนวนฟีโบนัชชี F_n ด้านล่าง

แม้รูปแบบที่เพิ่งอธิบายไปให้ต้องพิสูจน์กรณีฐาน เราไม่จำเป็นต้องพิสูจน์หากสามารถพิสูจน์ P(m) (โดยสมมติ P(n) สำหรับค่า n ที่น้อยกว่าทุกค่า) ได้สำหรับค่า m ≥ 0 ทุกตัว นี่เป็นกรณีพิเศษของการอุปนัยเชิงอนันต์อย่างที่อธิบายไว้ด้านล่าง ในรูปแบบนี้กรณีฐานถูกรวมอยู่ในกรณี m = 0 ซึ่ง P(0) ถูกพิสูจน์โดยไม่มีการสมมติ P(n) อื่น เราอาจต้องจัดการกับกรณีนี้แยกไปแต่บางครั้งการอ้างเหตุผลเดียวกันใช้ได้กับ m = 0 และ m > 0 ซึ่งทำให้การพิสูจน์เรียบง่ายและสวยงามกว่า อย่างไรก็ตามก็เป็นสิ่งที่สำคัญที่จะรับประกันว่าการพิสูจน์ P(m) ไม่ได้สมมติโดยนัยว่า m > 0 เช่นด้วยการบอกว่า "เลือกจำนวน n < m ค่าหนึ่ง" หรือด้วยการสมมติว่าเซตซึ่งมีสมาชิกจำนวน m มีสมาชิกหนึ่งตัว

การอุปนัยอย่างเข้มสมมูลกับการอุปนัยเชิงคณิตศาสตร์แบบธรรมดาอย่างที่อธิบายไว้ด้านบนในแง่ที่สามารถแปลงการพิสูจน์ด้วยวิธีการหนึ่งไปเป็นการพิสูจน์ด้วยอีกวิธีได้ สมมุติว่ามีการพิสูจน์ P(n) ด้วยการอุปนัยอย่างเข้ม ให้ Q(n) หมายถึง "P(m) เป็นจริงสำหรับค่า m ใด ๆ โดยที่ 0 ≤ m ≤ n" แล้ว Q(n) จะเป็นจริงสำหรับ n ทุกค่าก็ต่อเมื่อ P(n) เป็นจริงสำหรับ n ทุกค่า และการพิสูจน์ P(n) ของเราก็ถูกแปลงเป็นการพิสูจน์ Q(n) ได้อย่างง่ายดายด้วยการอุปนัย (แบบธรรมดา) ในทางกลับกันหาก P(n) ได้ถูกพิสูจน์โดยการอุปนัยธรรมดาแล้ว การพิสูจน์นั้นกลายเป็นอันที่ทำด้วยการอุปนัยแบบเข้มแล้วโดยประสิทธิผล: P(0) ถูกพิสูจน์ในกรณีฐานโดยไม่ใช้สมมติฐานและ P(n + 1) ถูกพิสูจน์ในขั้นตอนอุปนัยแล้วซึ่งอาจมีการสมมุติกรณีก่อนหน้านี้ทั้งหมดแต่ต้องใช้เพียงกรณี P(n) เท่านั้น

ตัวอย่าง: จำนวนฟีโบนัชชี

การอุปนัยอย่างเข้มมีประโยชน์สูงสุกเมื่อต้องใช้สมมติฐานอุปนัยหลาย ๆ รอบต่อขั้นตอนอุปนัยขั้นคอนหนึ่ง เช่นเราสามารถการอุปนัยอย่างเข้มเพื่อแสดงให้เห็นว่า

$F_{n}={\frac {\varphi ^{n}-\psi ^{n}}{\varphi -\psi }}$

ซึ่ง $F_{n}$ เป็นจำนวนฟีโบนัชชีจำนวนที่ n, ${\textstyle \varphi ={{1+{\sqrt {5}}} \over 2}}$ (อัตราส่วนทอง) และ ${\textstyle \psi ={{1-{\sqrt {5}}} \over 2}}$ เป็นรากของพหูพจน์ $x^{2}-x-1$ เอกลักษณ์ด้านบนสามารถถูกพิสูจน์ยืนยันด้วยการคำนวณ ${\textstyle F_{n+2}}$ โดยตรงหากเราสมมุติว่า ${\textstyle F_{n+1}}$ and ${\textstyle F_{n}}$ เป็นจริงอยู่แล้วด้วยการใช้ข้อเท็จจริงว่า $F_{n+2}=F_{n+1}+F_{n}$ สำหรับ $n\in {\mathbb {N}}$ แต่ละตัว เพื่อให้การพิสูจน์เสร็จสมบูรณ์ เอกลักษณ์จะต้องถูกพิสูจน์ยืนยันในกรณีฐานทั้งสองกรณี: $n=0$ และ ${\textstyle n=1}$

ตัวอย่าง: การแยกตัวประกอบเฉพาะ

การพิสูจน์ด้วยการอุปนัยอย่างเข้มอีกอันหนึ่งใช้สมมติฐานว่าข้อความเป็นจริงสำหรับจำนวน $n$ ทุกค่าที่น้อยกว่าอย่างถี่ถ้วนกว่า พิจารณาข้อความที่ว่า "จำนวนธรรมชาติทุกจำนวนซึ่งมากกว่า 1 เป็นผลคูณของจำนวนเฉพาะ (หนึ่งจำนวนหรือมากกว่า)" ซึ่งเป็นส่วน "การมีจริง" (existence) ของทฤษฎีบทมูลฐานของเลขคณิต สำหรับการพิสูจน์ขั้นตอนอุปนัยสมมติฐานอุปนัยคือสำหรับค่า $n>1$ ซึ่งกำหนดมาข้อความจะเป็นจริงสำหรับค่า $n>1$ ซึ่งน้อยกว่าทุกค่า หาก $m$ เป็นจำนวนเฉพาะแล้วมันเป็นผลคูณของจำนวนเฉพาะอย่างแน่นอน และหากไม่ใช่แล้วก็จะเป็นผลคูณ $m=n_{1}n_{2}$ โดยนิยามโดยตัวประกอบทั้งสองไม่เท่ากับ 1 ดังนั้นทั้งสองจึงไม่เท่ากับ $m$ เพราะฉะนั้นทั้งสองจึงมากกว่าหนึ่งและน้อยกว่า $m$ สมมติฐานอุปนัยตอนนี้ใช้ได้กับ $n_{1}$ และ $n_{2}$ ดังนั้นทั้งสองแต่ละตัวเป็นผลคูณของจำนวนเฉพาะ ฉะนั้น $m$ เป็นผลคูณของผลคูณของจำนวนเฉพาะและจึงเป็นผลคูณของจำนวนเฉพาะเองโดยการขยาย

ตัวอย่าง: กลับมาหาจำนวนเงินบาท

เราสมควรที่จะดูการพิสูจน์ตัวอย่างเดียวกับด้านบนครั้งนี้ด้วย การอุปนัยอย่างเข้ม ข้อความยังคงเดิม:

$S(n):\,\,n\geq 12\to \,\exists \,a,b\in \mathbb {N} .\,\,n=4a+5b$

แต่ทว่าโครงสร้างและสมมติฐานของการพิสูจน์จะมีความแตกต่างเล็กน้อย เริ่มจากกรณีฐานแบบขยาย:

กรณีฐาน: แสดงให้เห็นว่า $S(k)$ เป็นจริงสำหรับค่า $k=12,13,14,15$.

${\begin{aligned}4\cdot 3+5\cdot 0=12\\4\cdot 2+5\cdot 1=13\\4\cdot 1+5\cdot 2=14\\4\cdot 0+5\cdot 3=15\end{aligned}}$

กรณีฐานเป็นจริง

สมมติฐานอุปนัย: กำหนดจำนวน $j>15$ ค่าหนึ่ง สมมติว่า $S(m)$ เป็นจริงสำหรับค่า $m$ ทุกค่าโดย $12\leq m<j$.

ขั้นตอนอุปนัย: พิสูจน์ว่า $S(j)$ เป็นจริง

การเลือกค่า $m=j-4$ และสังเกตว่า $15<j\to 12\leq j-4<j$ แสดงให้เห็นว่า $S(j-4)$ เป็นจริงโดยสมมติฐานอุปนัย นั่นคือผลบวก $j-4$ สามารถถูกสร้างขึ้นมาด้วยส่วนผสมของเหรียญ $4$ และ $5$ บาท แล้วดังนั้นเพียงแค่เพิ่มเหรียญ $4$บาทลงไปในกองเหรียญนั้นแล้วก็จะให้ผลเป็นผลบวก $j$ นั่นก็คือ $S(j)$ เป็นจริง ∎

การอุปนัยคืบหน้า-ถอยหลัง

บางครั้งการนิรนัยถอยหลังคือการพิสูจน์ข้อความสำหรับ $n-1$ เมื่อพิจารณาความสมเหตุสมผลของมันสำหรับ $n$ จะสะดวกกว่า อย่างไรก็ตามการไม่พิสูจน์ความสมเหตุสมผลของข้อความสำหรับเลขตัวใดเพียงพอเพื่อสร้างกรณีฐาน เราต้องพิสูจน์ข้อความสำหรับเซตย่อยของจำนวนธรรมชาติไม่มีสิ้นสุดแทน เช่น โอกุสแต็ง-หลุยส์ โกชี (Augustin Louis Cauchy) ใช้การอุปนัยคืบหน้า (ปรกติ) เพื่อพิสูจน์อสมการมัชฌิมเลขคณิต-เรขาคณิต (inequality of arithmetic and geometric means) สำหรับกำลังของ 2 ทุกค่า แล้วใช้การอุปนัยถอยหลังเพื่อแสดงให้เห็นว่าเป็นจริงสำหรับจำนวนธรรมชาติทุกจำนวนด้วย

ตัวอย่างของความผิดพลาดในขั้นตอนอุปนัย

บทความหลัก: ม้าทุกตัวมีสีเดียวกัน

ขั้นตอนอุปนัยจะต้องถูกพิสูจน์สำหรับ n ทุกค่า เพื่อแสดงสิ่งนี้ให้เห็น โจเอล อี. โคเฮน ได้นำเสนอการอ้างเหตุผลว่าสามารถพิสูจน์ว่าม้าทุกตัวมีสีเดียวกัน (All horses are the same color) ได้ด้วยการอุปนัยเชิงคณิตศาสตร์ได้ดังต่อไปนี้:

• กรณีฐาน: ในเซตของม้าแค่หนึ่งตัว จะมีสีแค่หนึ่งสี
• ขั้นตอนอุปนัย: สมมติว่าในเซตของม้า $n$ ตัวเซตใด ๆ ก็จะมีสีเพียงหนึ่งสีเป็นสมมติฐานอุปนัย คราวนี้ดูที่เซตของม้า $n+1$ ตัว ใส่ลำดับเลขแต่ละตัวเป็น: $1,\;2,\;3,\;\dotsc ,\;n,\;n+1$ พิจารณาเซต ${\textstyle \left\{1,\;2,\;3,\;\dotsc ,\;n\right\}}$ และ ${\textstyle \left\{2,\;3,\;4,\;\dotsc ,\;n+1\right\}}$ แต่ละเซตเป็นเซตของม้า $n$ ตัวเพราะฉะนั้นจึงมีสีเพียงสีเดียวในแต่ละเซตและทั้งสองเซตเหลื่อมกัน ม้า $n+1$ ตัวทุกตัวจึงจะต้องมีสีเพียงสีเดียวเท่านั้น

กรณีฐาน $n=1$ เป็นเรื่องธรรมดา (เพราะไม่ว่าม้าตัวไหนก็จะมีสีเดียวกับตัวมันเอง) และขั้นตอนอุปนัยถูกต้องในกรณีที่ $n>1$ ทุกกรณี แต่ทว่าตรรกะของขั้นตอนอุปนัยสำหรับค่า $n=1$ ไม่ถูกต้องเพราะข้อความที่ว่า "ทั้งสองเซตเหลื่อมกัน" เป็นเท็จ (มีม้าเพียง $n+1=2$ ตัวทั้งก่อนและหลังการเอาม้าตัวหนึ่งออกจากเซต เซตของม้าตัวเดียวจึงไม่เหลื่อมกัน)

การกำหนดรูป

เราสามารถเขียน "สัจพจน์ของการอุปนัย" ในตรรกะอันดับสอง (second-order logic) ได้ดังนี้:

$\displaystyle \forall P{\Bigl (}P(0)\land \forall k{\bigl (}P(k)\to P(k+1){\bigr )}\to \forall n{\bigl (}P(n){\bigr )}{\Bigr )}$,

ซึ่ง P(.) เป็นตัวแปรของภาคแสดงซึ่งมีจำนวนธรรมชาติหนึ่งตัวและ k กับ n เป็นตัวแปรของจำนวนธรรมชาติ is a variable

อธิบายเป็นลายลักษณ์อักษรได้ว่า กรณีฐาน P(0) และขั้นตอนอุปนัย (กล่าวคือ สมมติฐานอุปนัย P(k) บอกเป็นนัย P(k + 1)) บอกเป็นนัยร่วมกันว่า P(n) สำหรับจำนวนธรรมชาติ n ใด ๆ สัจพจน์ของการอุปนัยยืนยันความสมเหตุสมผลของการอนุมานว่า P(n) เป็นจริงสำหรับจำนวนธรรมชาติ n ใด ๆ จากกรณีฐานและขั้นตอนอุปนัย

ตัวบ่งปริมาณตัวแรกในสัจพจน์ครอบคลุมถึงภาคแสดงแทนที่จะเป็นตัวเลขแต่ละตัว นี่เป็นตัวบ่งปริมาณอันดับสองซึ่งแปลว่าสัจพจน์นี้ถูกกล่าวในตรรกะอันดับสอง การกำหนดสัจพจน์การอุปนัยเลขคณิตในตรรกะอันดับหนึ่ง (first-order logic) จำเป็นต้องมีเค้าร่างสัจพจน์ (Axiom schema) ซึ่งประกอบขึ้นด้วยสัจพจน์ซึ่งแยกจากกันสำหรับภาคแสดงที่เป็นไปได้แต่ละภาค บทความสัจพจน์เปอาโน (Peano axioms) พูดถึงประเด็นนี้เพิ่มเติม

สัจพจน์ของการอุปนัยเชิงโครงสร้างสำหรับจำนวนธรรมชาติถูกกำหนดรูปเป็นครั้งแรกโดยเปอาโนผู้ซึ่งใช้มันเพื่อระบุจำนวนธรรมชาติเข้าด้วยกันด้วยสัจพจน์อื่นสี่ข้อดังต่อไปนี้:

1. 0 เป็นจำนวนธรรมชาติ
2. ฟังก์ชันตัวตามหลัง s ของจำนวนธรรมชาติใด ๆ ให้ผลออกมาเป็นจำนวนธรรมชาติ (s(x)=x+1).
3. ฟังก์ชันตัวตามหลังเป็นหนึ่งต่อหนึ่ง
4. 0 ไม่ได้อยู่ในพิสัยของ s

การบ่งปริมาณกับภาคแสดงทำไม่ได้ในทฤษฎีเซตแซร์เมโล-เฟรนเคิลอันดับหนึ่ง (Zermelo-Fraenkel set theory) แต่เรายังสามารถแสดงการอุปนัยด้วยการบ่งปริมาณกับเซต:

$\forall A{\Bigl (}0\in A\land \forall k\in \mathbb {N} {\bigl (}k\in A\to (k+1)\in A{\bigr )}\to \mathbb {N} \subseteq A{\Bigr )}$

เราสามารถอ่าน $A$ เป็นเซตซึ่งแทนประพจน์และมีจำนวนธรรมชาติสำหรับที่ประพจน์เป็นจริง นี่ไม่ใช่สัจพจน์แต่เป็นทฤษฎีบทคล้ายกับของเปอาโน โดยกำหนดว่าจำนวนธรรมชาติถูกนิยามในภาษาของทฤษฎีเซต ZFC ด้วยสัจพจน์

การอุปนัยเชิงอนันต์

บทความหลัก: การอุปนัยเชิงอนันต์

(อังกฤษ: Transfinite induction) เราสามารถนำหลักการของการอุปนัยอย่างเข้มมาใช้กับข้อความเกี่ยวกับสมาชิกของเซตรากฐานดี (Well-founded set) เซตใด ๆ ได้ด้วยนอกเหนือจากข้อความเกี่ยวกับจำนวนธรรมชาติเท่านั้น นั่นคือเซตซึ่งมีความสัมพันธ์ไม่สะท้อน (irreflexive relation) ซึ่งไม่มีเซตอันดับทุกส่วนลดหลั่นอนันต์ (infinite descending chain) เซตของจำนวนเชิงการนับเซตใด ๆ เป็นเซตรากฐานดีซึ่งรวมไปถึงเซตของจำนวนธรรมชาติ เมื่อนำไปประยุกต์กับเซตรากฐานดีก็สามารถกำหนดรูปใหม่เป็นขั้นตอนเดียวได้ว่า:

1. แสดงให้เห็นว่าหากข้อความข้อหนึ่งเป็นจริงสำหรับค่า m < n ค่าใด ๆ แล้วข้อความเดียวกันนั้นก็จะเป็นจริงสำหรับ n ด้วย

เมื่อนำการอุปนัยรูปนี้ไปประยุกต์ใช้กับเซตของจำนวนเชิงอันดับที่แล้ว (ซึ่งทำให้เกิดคลาสอันดับดี (well-order) และจึงเป็นคลาสรากฐานดี) ก็จะเรียกว่าการอุปนัยเชิงอนันต์ นี่เป็นเทคนิคการพิสูจน์ที่สำคัญในทฤษฎีเซต ทอพอโลยีและสาขาวิชาอื่น ๆ

การพิสูจน์โดยการอุปนัยเชิงอนันต์โดยปกติแล้วจะจำแนกกรณีเป็นสามกรณี:

1. เมื่อ n เป็นสมาชิกเล็กสุด หรือก็คือไม่มีสมาชิกซึ่งเล็กไปกว่า n อีก
2. เมื่อ n มีตัวนำหน้าโดยตรง หรือก็คือเซตของสมาชิกซึ่งเล็กกว่า n มีสมาชิกใหญ่สุด
3. เมื่อ n ไม่มีตัวนำหน้าโดยตรง หรือก็คือ n เป็นสิ่งที่เรียกกันว่าจำนวนเชิงอันดับที่จำกัด (limit ordinal)

หากพูดให้ชัดเจน มันไม่จำเป็นที่จะต้องพิสูจน์กรณีฐานในการอุปนัยเชิงอนันต์เพราะมันเป็นกรณีพิเศษว่างเปล่า (Vacuous truth) ของประพจน์ว่าหาก P เป็นจริงสำหรับค่า n < m ทุกค่าแล้ว P จะเป็นจริงสำหรับ m มันเป็นจริงอย่างว่างเปล่าก็เป็นเพราะว่าไม่มีค่า n < m ค่าใดซึ่งสามารถทำหน้าที่เป็นตัวอย่างขัดแย้งได้

ความสัมพันธ์กับหลักการจัดอันดับดี

หลักการอุปนัยเชิงคณิตศาสตร์มักถูกกล่าวว่าเป็นสัจพจน์ข้อหนึ่งของจำนวนธรรมชาติ (ดูที่สัจพจน์เปอาโน) หลักการนี้แรงกว่าหลักการจัดอันดับดี (Well-ordering principle) ในบริบทของสัจพจน์เปอาโนอื่น ๆ สมมุติสิ่งต่าง ๆ ดังต่อไปนี้:

• สัจพจน์ไตรวิภาค (trichotomy (mathematics)): n น้อยกว่าหรือเท่ากับ m ก็ต่อเมื่อ m ไม่น้อยกว่า n สำหรับจำนวนธรรมชาติ n และ m ใด ๆ
• n + 1 มากกว่า n สำหรับจำนวนธรรมชาติ n ใด ๆ
• ไม่มีจำนวนธรรมชาติที่อยู่ระหว่าง n และ n + 1 สำหรับจำนวนธรรมชาติ n ใด ๆ
• ไม่มีจำนวนธรรมชาติที่น้อยกว่าศูนย์

จากนั้นก็จะสามารถพิสูจน์ด้วยสัจพจน์ที่ทำรายการไว้ด้านบนได้ว่าการอุปนัยบอกเป็นนัยถึงหลักการจัดอันดับดี การพิสูจน์ดังต่อไปนี้ใช้การอุปนัยอย่างเข้มและสัจพจน์ข้อที่หนึ่งและสี่

การพิสูจน์ สมมติว่ามีเซตของจำนวนธรรมชาติที่ไม่มีสมาชิกเล็กสุด S ซึ่งไม่ว่างอยู่เซตหนึ่ง ให้ P(n) เป็นข้อความยืนยันว่าไม่มี n อยู่ใน S แล้ว P(0) จะเป็นจริงเพราะไม่เช่นนั้น 0 ก็จะกลายเป็นสมาชิกเล็กสุดของ S จากนั้นให้ n เป็นจำนวนธรรมชาติและสมมติว่า P(m) เป็นจริงสำหรับจำนวนธรรมชาติ m ทุกตัวที่มีค่าน้อยกว่า n+1 ฉะนั้นหาก P(n+1) เป็นเท็จ n+1 จะอยู่ใน S และจึงเป็นสมาชิกน้อยสุดของ S ซึ่งเป็นการขัดแย้ง ดังนั้น P(n+1) จึงเป็นจริง เพราะฉะนั้น P(n) เป็นจริงสำหรับจำนวนธรรมชาติ n ทุกตัวโดยหลักการอุปนัยอย่างเข้ม และ S จึงเป็นเซตว่างซึ่งก็เป็นการขัดแย้ง ∎

"เส้นจำนวน" สำหรับเซต {(0,n): n∈ℕ} ∪ {(1,n): n∈ℕ} ตัวเลขอ้างอิงถึงส่วนประกอบส่วนที่สองของคู่อันดับ ส่วนประกอบส่วนที่หนึ่งสามารถรู้ได้จากสีหรือตำแหน่ง

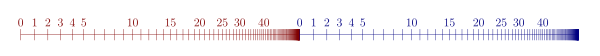
ในทางกลับกันเซต {(0,n): n∈ℕ} ∪ {(1,n): n∈ℕ} ซึ่งแสดงอยู่ในรูปมีอันดับดีโดยอันดับพจนานุกรม (lexicographic order) มากไปกว่านั้นยังสอดคล้องกับสัจพจน์เปอาโนทุกประการยกเว้นสัจพจน์อุปนัย โดยค่าคงตัว 0 ของเปอาโนถูกตีความเป็นคู่อันดับ (0,0) และฟังก์ชันตัวตามหลังของเปอาโนถูกนิยามไว้สำหรับคู่อันดับเป็น succ(x,n)=(x,n+1) สำหรับ x∈{0,1} และ n∈ℕ ทุกตัว เพื่อเป็นตัวอย่างสำหรับการฝ่าฝืนสัจพจน์อุปนัยให้นิยามภาคแสดง P(x,n) เป็น (x,n)=(0,0) หรือ (x,n)=(succ(y,m)) สำหรับ y∈{0,1} และ m∈ℕ บางตัว แล้วกรณีฐาน P(0,0) จะเป็นจริงโดยธรรมดาและขั้นตอนอุปนัยก็เป็นจริงด้วย: หาก P(x,n) แล้ว P(succ(x,n)) แต่ทว่ากลับไม่เป็นจริงสำหรับคู่อันดับทุกคู่ในเซต

สัจพจน์ของเปอาโนกับหลักการอุปนัยจำลองแบบจำนวนธรรมชาติโดยเฉพาะ การเปลี่ยนหลักการอุปนัยเป็นหลักการจัดอันดับดีทำให้สามารถสร้างแบบจำลองที่แตกต่างมากขึ้นซึ่งสอดคล้องกับสัจพจน์ทุกประการ

ในหนังสือและแหล่งข้อมูลหลายแห่งใส่ข้อมูลที่ผิดพลาดไว้ว่าหลักการจัดอันดับดีนั้นสมมูลกับสัจพจน์อุปนัย แต่ทว่านี่ไม่เป็นจริงในบริบทของสัจพจน์เปอาโนข้ออื่น ๆ แต่ในสัจพจน์อื่น ๆ จะสมมูลกัน หลักการจัดอันดับดีบอกเป็นนัยสัจพจน์อุปนัยในบริบทของสัจพจน์ซึ่งเรียงลำดับไว้ด้านบนสองข้อแรกและ

• จำนวนธรรมชาติทุกจำนวนไม่เป็น 0 ก็เป็น n + 1 สำหรับจำนวนธรรมชาติ n จำนวนใดจำนวนหนึ่ง

ข้อผิดพลาดซึ่งพบได้บ่อยในการพิสูจน์ซึ่งเข้าใจผิดคือการสมมติว่า n − 1 เป็นจำนวนธรรมชาติที่เป็นได้อย่างเดียวและถูกนิยามไว้อย่างดีซึ่งเป็นคุณสมบัติที่สัจพจน์เปอาโนข้ออื่น ๆ ไม่ได้บอกเป็นนัย

ดูเพิ่ม

• การพิสูจน์เชิงการจัด (Combinatorial proof)
• ปริศนาอุปนัย (Induction puzzles)
• การพิสูจน์โดยการแจงกรณี (Proof by exhaustion)
• การเรียกซ้ำ
• การเรียกซ้ำ (วิทยาการคอมพิวเตอร์) (recursion (computer science))
• การอุปนัยเชิงโครงสร้าง (Structural induction)
• การอุปนัยเชิงอนันต์ (Transfinite induction)

บรรณานุกรม

บทนำ

• Franklin, J.; Daoud, A. (2011). Proof in Mathematics: An Introduction. Sydney: Kew Books. ISBN 978-0-646-54509-7. (Ch. 8.)
• Hazewinkel, Michiel, บ.ก. (2001), "Mathematical induction", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
• Hermes, Hans (1973). Introduction to Mathematical Logic. Hochschultext. London: Springer. ISBN 978-3540058199. ISSN 1431-4657. MR 0345788.
• Knuth, Donald E. (1997). The Art of Computer Programming, Volume 1: Fundamental Algorithms (3rd ed.). Addison-Wesley. ISBN 978-0-201-89683-1. (Section 1.2.1: Mathematical Induction, pp. 11–21.)
• Kolmogorov, Andrey N.; Fomin, Sergei V. (1975). Introductory Real Analysis. Silverman, R. A. (trans., ed.). New York: Dover. ISBN 978-0-486-61226-3. (Section 3.8: Transfinite induction, pp. 28–29.)

ประวัติ

• Acerbi, Fabio (Aug 2000). "Plato: Parmenides 149a7-c3. A Proof by Complete Induction?". Archive for History of Exact Sciences. 55 (1): 57–76. doi:10.1007/s004070000020. JSTOR 41134098. S2CID 123045154.
• Bussey, W. H. (1917). "The Origin of Mathematical Induction". The American Mathematical Monthly. 24 (5): 199–207. doi:10.2307/2974308. JSTOR 2974308.
• Cajori, Florian (1918). "Origin of the Name "Mathematical Induction"". The American Mathematical Monthly. 25 (5): 197–201. doi:10.2307/2972638. JSTOR 2972638.
• Fowler, D. (1994). "Could the Greeks Have Used Mathematical Induction? Did They Use It?". Physis. 31: 253–265.
• Freudenthal, Hans (1953). "Zur Geschichte der vollständigen Induction". Archives Internationales d'Histoire des Sciences. 6: 17–37.
• Katz, Victor J. (1998). History of Mathematics: An Introduction. Addison-Wesley. ISBN 0-321-01618-1.
• Peirce, Charles Sanders (1881). "On the Logic of Number". American Journal of Mathematics. 4 (1–4): 85–95. doi:10.2307/2369151. JSTOR 2369151. MR 1507856. Reprinted (CP 3.252–288), (W 4:299–309)
• Rabinovitch, Nachum L. (1970). "Rabbi Levi Ben Gershon and the origins of mathematical induction". Archive for History of Exact Sciences. 6 (3): 237–248. doi:10.1007/BF00327237. MR 1554128. S2CID 119948133.
• Rashed, Roshdi (1972). "L'induction mathématique: al-Karajī, as-Samaw'al". Archive for History of Exact Sciences (ภาษาฝรั่งเศส). 9 (1): 1–21. doi:10.1007/BF00348537. MR 1554160. S2CID 124040444.
• Rashed, R. (1994). "Mathematical induction: al-Karajī and al-Samawʾal". The Development of Arabic Mathematics: Between Arithmetic and Algebra. Boston Studies in the Philosophy of Science (ภาษาอังกฤษ). Vol. 156. Springer Science & Business Media. ISBN 9780792325659.
• Shields, Paul (1997). "Peirce's Axiomatization of Arithmetic". ใน Houser, Nathan; Roberts, Don D.; Evra, James Van (บ.ก.). Studies in the Logic of Charles S. Peirce. Indiana University Press. pp. 43–52. ISBN 0-253-33020-3. MR 1720827.
• Simonson, Charles G. (Winter 2000). "The Mathematics of Levi ben Gershon, the Ralbag" (PDF). Bekhol Derakhekha Daehu. Bar-Ilan University Press. 10: 5–21. คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2017-10-11. สืบค้นเมื่อ 2020-12-27.
• Unguru, S. (1991). "Greek Mathematics and Mathematical Induction". Physis. 28: 273–289.
• Unguru, S. (1994). "Fowling after Induction". Physis. 31: 267–272.
• Vacca, G. (1909). "Maurolycus, the First Discoverer of the Principle of Mathematical Induction". Bulletin of the American Mathematical Society. 16 (2): 70–73. doi:10.1090/S0002-9904-1909-01860-9. MR 1558845.
• Yadegari, Mohammad (1978). "The Use of Mathematical Induction by Abū Kāmil Shujā' Ibn Aslam (850-930)". Isis. 69 (2): 259–262. doi:10.1086/352009. JSTOR 230435. S2CID 144112534.