เออีเอส
 ขั้น SubBytes เป็นขั้นหนึ่งในสี่ขั้นที่ใช้เข้ารหัสเออีเอสรอบหนึ่ง | |
| ทั่วไป | |
|---|---|
| ผู้ออกแบบ | วินเซ็นต์ เรเม็น, โจน แดเม็น |
| เผยแพร่ | 1998 |
| แบบอนุพัทธ์ของ | Square |
| แบบที่เป็นอนุพัทธ์ | Anubis, Grand Cru, Kalyna |
| การรับรอง | AES winner, CRYPTREC, NESSIE, NSA |
| รายละเอียดของไซเฟอร์ | |
| ขนาดกุญแจ | 128, 192 หรือ 256 บิต[A] |
| ขนาดบล็อก | 128 บิต[B] |
| โครงสร้าง | Substitution-permutation network |
| รอบการคำนวณ | 10, 12 หรือ 14 รอบ (ขึ้นอยู่กับขนาดกุญแจ) |
| การวิเคราะห์รหัสลับที่ได้ผลดีสุดดังที่เปิดเผย | |
| มีวิธีการโจมตีต่าง ๆ ที่คำนวณได้เร็วกว่าการโจมตีด้วยกำลังอย่างเดียว (brute-force attack) แต่จนถึงปี 2013 ก็ยังไม่มีวิธีที่นำไปใช้กับคอมพิวเตอร์ที่มีได้จริง ๆ[1]
สำหรับ AES-128 กุญแจสามารถหาได้ด้วยวิธีที่มีความซับซ้อนเชิงคำนวณที่ 2126.1 โดยใช้ biclique attack ถ้าใช้วิธีเดียวกันต่อ AES-192 และ AES-256 ความซับซ้อนจะอยู่ที่ 2189.7 และ 2254.4 ตามลำดับ ส่วน related-key attack[C] สามารถเจาะ AES-192 และ AES-256 โดยมีความซับซ้อนเชิงคำนวณที่ 2176 และ 299.5 ตามลำดับ ไม่ว่าจะโดยเวลาหรือโดยข้อมูล[2] | |
เออีเอส ซึ่งเป็นตัวย่อของ Advanced Encryption Standard (AES) ที่มีชื่อดั้งเดิมว่า Rijndael (เสียงอ่านภาษาดัตช์: [ˈrɛindaːl] อ่านว่า เรนดาล)[3] เป็นมาตรฐานการเข้ารหัสลับข้อมูลอิเล็กทรอนิกที่ตั้งขึ้นโดยสถาบันมาตรฐานและเทคโนโลยีแห่งชาติสหรัฐ (NIST) ในปี 2001[4]
เออีเอสเป็นส่วนย่อยของกลุ่มบล็อกไซเฟอร์ (block cipher)[D] ที่เรียกว่าเรนดาล (Rijndael)[3] และพัฒนาโดยนักวิทยาการเข้ารหัสลับชาวเบลเยียมสองท่าน คือวินเซ็นต์ เรเม็น (Vincent Rijmen) และโจน แดเม็น (Joan Daemen) ผู้ส่งวิธีการเป็นข้อเสนอ[5] แก่ NIST เมื่อองค์กรกำลังเลือกไซเฟอร์ (cipher)[E] เพื่อใช้เป็นเออีเอส[6] เรนดาลเป็นกลุ่มไซเฟอร์ที่มีกุญแจและบล็อก (block) ขนาดต่าง ๆ
เพื่อใช้เป็นมาตรฐานเออีเอส NIST ได้เลือกสมาชิก 3 หน่วยจากกลุ่มเรนดาล แต่ละอย่างมีขนาดบล็อก 128 บิตโดยมีกุญแจขนาดต่าง ๆ คือ 128, 192 และ 256 บิต รัฐบาลกลางสหรัฐได้เลือกใช้มาตรฐานนี้ และปัจจุบันก็ใช้กันทั่วโลก เป็นมาตรฐานแทน Data Encryption Standard (DES)[7] ซึ่งเผยแพร่ในปี 1977 AES ใช้ขั้นตอนวิธีแบบกุญแจสมมาตร (symmetric-key algorithm) คือ ใช้กุญแจตัวเดียวกันเพื่อทั้งเข้ารหัสและถอดรหัสข้อมูล
ในสหรัฐ NIST ได้ประกาศเออีเอสเป็นมาตรฐานประมวลข้อมูลรัฐบาลกลางสหรัฐ (FIPS 197) เมื่อปลายปี 2001[4] นี่ทำตามหลังกระบวนการวางมาตรฐาน ซึ่งมีแบบที่เข้าแข่งขันกัน 15 แบบ เมื่อประเมินแล้วไซเฟอร์เรนดาลจึงได้เลือกว่าเหมาะสมที่สุด
เออีเอสจึงกลายเป็นมาตรฐานรัฐบาลกลางสหรัฐเมื่อกลางปี 2002 หลังจากได้รับอนุมัติจากเลขาธิการกระทรวงพาณิชย์สหรัฐ เออีเอสได้รวมเข้ามาตรฐานขององค์การระหว่างประเทศว่าด้วยการมาตรฐาน (ISO) และ International Electrotechnical Commission (IEC) คือ ISO/IEC 18033-3 standard เออีเอสมีใช้ในคลัง/โปรแกรมเข้ารหัสสำเร็จหลายอย่าง เป็นไซเฟอร์ที่สาธารณชนเข้าถึงได้เดียวที่สำนักงานความมั่นคงแห่งชาติสหรัฐ (NSA) อนุมัติให้ใช้เข้ารหัสข้อมูลราชการลับระดับ "top secret" โดยต้องใช้มอดูลเข้ารหัสที่องค์กรได้อนุมัติ
มาตรฐาน
[แก้]เออีเอสได้กำหนดในมาตรฐานต่าง ๆ ดังต่อไปนี้
ไซเฟอร์
[แก้]เออีเอสใช้หลักที่เรียกว่า substitution-permutation network (เครือข่ายการแทนที่-การเรียงสับเปลี่ยน) ซึ่งมีประสิทธิภาพดีเมื่อทำให้เกิดผลทั้งในซอฟต์แวร์และฮาร์ดแวร์[9] ไม่เหมือนกับมาตรฐานก่อนคือ DES เออีเอสไม่ได้ใช้เครือข่ายฟายสเติล (Feistel network)[F] เออีเอสเป็นรูปแปรของเรนดาลแต่มีขนาดบล็อกตายตัวที่ 128 บิต และขนาดกุญแจที่ 128, 192 หรือ 256 บิต เทียบกับเรนดาลที่กำหนดขนาดบล็อกและขนาดกุญแจที่เป็นพหุคูณ 32 บิตใด ๆ ก็ได้โดยน้อยสุดที่ 128 บิตและมากสุดที่ 256 บิต เออีเอสคำนวณโดยใช้แถวลำดับขนาด 4 × 4 เก็บต่อกันในความจำเรียงอันดับตามสดมภ์ (column-major order[G]) เป็นหน่วยที่เรียกว่า "สเตต" (state)[H] การคำนวณเออีเอสโดยมากจะทำในฟิลด์จำกัด (finite field)[I] ยกตัวอย่างเช่น ถ้ามีไบต์ 16 ไบต์ คือ ก็สามารถแสดงเป็นแถวลำดับสองมิติ คือ
ขนาดกุญแจที่ใช้ในไซเฟอร์เออีเอสจะระบุจำนวนรอบการแปลง (transformation round) ที่เปลี่ยนอินพุตซึ่งเรียกว่า ข้อความธรรมดา (plaintext) เป็นเอาต์พุตสุดท้ายซึ่งเรียกว่า ข้อความไซเฟอร์ (ciphertext) จำนวนรอบที่ต้องคำนวณ คือ
- 10 รอบสำหรับกุญแจขนาด 128 บิต
- 12 รอบสำหรับกุญแจขนาด 192 บิต
- 14 รอบสำหรับกุญแจขนาด 256 บิต
แต่ละรอบจะมีขั้นประมวลผลหลายขั้น รวมทั้งขั้นที่ต้องอาศัยกุญแจการเข้ารหัส การถอดรหัสจะใช้รอบกลับกันเพื่อเปลี่ยนข้อความไซเฟอร์กลับไปเป็นข้อความธรรมดาดั้งเดิมด้วยกุญแจเดียวกัน
ขั้นตอนวิธีคร่าว ๆ
[แก้]- KeyExpansion (การขยายจำนวนกุญแจ) —กุญแจที่ใช้ในแต่ละรอบจะทำจากกุญแจสมมาตรด้วยขั้นตอนวิธี Rijndael key schedule[J] เออีเอสต้องใช้บล็อกกุญแจขนาด 128 บิตหนึ่งบล็อกต่างหาก (round key block - บล็อกกุญแจรอบ) สำหรับการคำนวณแต่ละรอบ บวกเพิ่มอีกหนึ่งตัว
- การบวกกุญแจรอบเบื้องต้น
- AddRoundKey—ไบต์แต่ละไบต์ของสเตตจะรวมเข้ากับบล็อกหนึ่งของกุญแจรอบด้วย bitwise xor
- ทำดังนี้ 9, 11 หรือ 13 รอบ
- SubBytes (แทนที่ไบต์)—ขั้นการแทนที่แบบไม่เชิงเส้น (non-linear)—ไบต์แต่ละไบต์จะแทนที่ด้วยไบต์อีกไบต์หนึ่งตามตารางค้นหา คือ Rijndael S-box[K]
- ShiftRows (เลื่อนแถว) —ขั้นการย้ายสดมภ์—แถวสุดท้าย 3 แถวของสเตตจะเลื่อนหมุนเป็นจำนวนหนึ่ง
- MixColumns (ผสมสดมภ์) —เป็นปฏิบัติการผสมเชิงเส้น ซึ่งดำเนินการต่อสดมภ์ของสเตต เป็นการรวมไบต์ 4 ไบต์ของสดมภ์แต่ละสดมภ์
- AddRoundKey
- รอบสุดท้าย (จึงรวมเป็น 10, 12 หรือ 14 รอบทั้งหมด)
- SubBytes
- ShiftRows
- AddRoundKey
ขั้น SubBytes
[แก้]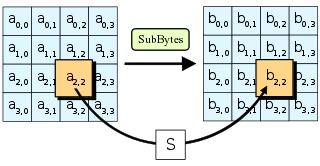
ในขั้น SubBytes ไบต์แต่ละไบต์ คือ ของสเตตจะแทนที่ด้วย SubByte โดยใช้ตารางค้นหา คือ substitution box (S-box)[L] แบบ 8 บิต ปฏิบัติการนี้ทำให้ได้ความไม่เป็นเชิงเส้น (non-linearity) ในไซเฟอร์ S-box ที่ใช้ได้มาจากตัวผกผันการคูณของฟิลด์จำกัด (28) ซึ่งรู้ว่ามีคุณสมบัติไม่ใช่เชิงเส้น (non-linearity) ที่ดี เพื่อหลีกเลี่ยงการโจมตีอาศัยคุณสมบัติพีชคณิตที่ง่าย ๆ S-box สร้างโดยรวมฟังก์ชันผกผัน (inverse function) กับการแปลงสัมพรรคที่หาตัวผกผันได้ (invertible affine transformation[M]) S-box ยังเลือกไม่ให้มีจุดตรึง (ดังนั้นจึงเป็น derangement[N]) คือ และไม่ให้มีจุดตรึงตรงกันข้าม คือ เมื่อถอดรหัส ขั้น InvSubBytes (ซึ่งเป็นฟังก์ชันผกผันของ SubBytes) จะต้องหาค่าผกผันของการแปลงสัมพรรคก่อนแล้วจึงหาตัวผกผันการคูณ
ขั้น ShiftRows
[แก้]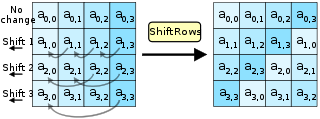
ขั้น ShiftRows ปฏิบัติการต่อแถวของสเตต คือเลื่อนหมุนไบต์แต่ละไบต์ของแถวไปช่วงระยะหนึ่ง โดยแถวแรกจะไม่เลื่อน แถวสองเลื่อนหมุนไปทางซ้ายหนึ่งช่อง โดยนัยเดียวกัน แถวสามและแถวสี่จะเลื่อนหมุนไป 2 และ 3 ช่องตามลำดับ[O] ด้วยวิธีนี้ สดมภ์แต่ละสดมภ์ของสเตตที่เป็นเอาต์พุตของขั้น ShiftRows จะประกอบด้วยไบต์จากสดมภ์ทุกสดมภ์ของสเตตที่เป็นอินพุต ขั้นนี้สำคัญเพราะเลี่ยงไม่ให้สดมภ์แต่ละสดมภ์เข้ารหัสลับอย่างเป็นอิสระจากกันและกัน ไม่งั้นแล้วเออีเอสก็จะเสื่อมเป็นบล็อกไซเฟอร์[D] 4 บล็อกที่เป็นอิสระจากกันและกัน
ขั้น MixColumns
[แก้]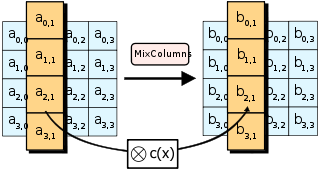
ส่วนนี้รอเพิ่มเติมข้อมูล คุณสามารถช่วยเพิ่มข้อมูลส่วนนี้ได้ |
ในขั้น MixColumns ไบต์สี่ไบต์จากสดมภ์แต่ละสดมภ์จะนำมารวมกันโดยใช้การแปลงเชิงเส้นที่หาตัวผกผันได้ (invertible linear transformation) ฟังก์ชัน MixColumns รับไบต์สี่ไบต์เป็นอินพุต และออกไบต์สี่ไบต์เป็นเอาต์พุต โดยไบต์อินพุตแต่ละไบต์จะมีผลต่อไบต์เอาต์พุตทั้งหมด เมื่อรวมกับขั้น ShiftRows ขั้น MixColumns นี้ให้คุณสมบัติความแพร่ (diffusion)[P] ต่อไซเฟอร์
ในปฏิบัติการนี้ สดมภ์แต่ละสดมภ์จะแปลงด้วยเมทริกซ์ เป็นการคูณเมทริกซ์มีค่าตายตัวกับสดมภ์โดยได้ผลเป็นค่าสดมภ์ใหม่ในสเตต
การ "คูณ" เมทริกซ์ประกอบด้วยการคูณและการบวกช่องในเมทริกซ์ การบวกใช้ปฏิบัติการ XOR ส่วนการคูณเป็นปฏิบัติการที่ซับซ้อน บทความนี้ไม่กล่าวถึงรายละเอียด
ขั้น AddRoundKey
[แก้]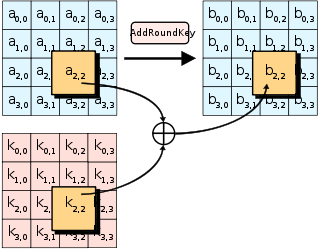
ในขั้น AddRoundKey กุญแจย่อย (subkey) จะรวมเข้ากับสเตต ในแต่ละรอบ กุญแจย่อยจะทำมาจากกุญแจหลักด้วยขั้นตอนวิธี Rijndael key schedule[J] กุญแจย่อยแต่ละตัวมีขนาดเท่ากับสเตต ไบต์แต่ละไบต์ของสเตตจะรวมเข้ากับไบต์ของกุญแจย่อยที่ตรงกันด้วย bitwise XOR
การเร่งความเร็ว
[แก้]ในระบบที่ใช้คำ (word) มีขนาด 32 บิตหรือยาวกว่า สามารถเร่งปฏิบัติการของไซเฟอร์นี้ด้วยการรวมขั้นตอน SubBytes และ ShiftRows กับ MixColumns โดยแปลงให้เป็นการค้นหาในตารางตามลำดับ ซึ่งใช้ตารางเก็บค่า 32 บิต มีรายการ 256 รายการ ทั้งหมด 4 ตาราง รวมใช้ที่ 4096 ไบต์ การคำนวณรอบหนึ่งจึงสามารถทำด้วยการค้นหาตาราง 16 ครั้ง และปฏิบัติการ XOR แบบ 32 บิต 12 ครั้ง ตามด้วยปฏิบัติการ XOR แบบ 32 บิต 4 ครั้งในขั้น AddRoundKey[13] อีกอย่างหนึ่ง การค้นหาตารางสามารถทำกับตารางเก็บค่า 32 บิตมีรายการ 256 รายการตารางเดียว (รวมใช้ที่ 1024 ไบต์) ตามด้วยการหมุนเป็นวง (circular rotation)
อนึ่ง ถ้าใช้วิธีทำเป็นไบต์ ก็จะสามารถรวมขั้น SubBytes, ShiftRows และ MixColumns เป็นปฏิบัติการเดียวต่อรอบ[14]
ความปลอดภัย
[แก้]จนถึงเดือนพฤษภาคม 2009 มีแต่การโจมตีแบบ side-channel attack[Q] เท่านั้นที่สามารถเจาะเออีเอสซึ่งเข้ารหัสแบบสมบูรณ์อย่างได้ผล โดยทำได้กับการทำให้เกิดผลเฉพาะบางอย่างเท่านั้น สำนักงานความมั่นคงแห่งชาติสหรัฐ (NSA) ได้ทบทวนไซเฟอร์[E]ที่เข้าแข่งขันทั้งหมดรวมทั้งเรนดาล และเบื้องต้นได้ระบุว่า ทั้งหมดปลอดภัยพอเข้ารหัสลับข้อมูลที่ไม่ใช่ราชการลับของรัฐบาลกลางสหรัฐ ต่อมาในเดือนมิถุนายน 2003 รัฐบาลกลางสหรัฐได้ประกาศว่า จะใช้เออีเอสป้องกันราชการลับ โดยระบุว่า
แบบและความเข้มแข็งของขั้นตอนวิธีเออีเอสโดยใช้กุญแจทุกขนาด (คือ 128, 192 และ 256 บิต) เพียงพอป้องกันราชการลับจนถึงระดับ SECRET ส่วนข้อมูลระดับ TOP SECRET ต้องใช้ขนาดกุญแจ 192 หรือ 256 (บิต)
การทำเออีเอสให้เกิดผลในผลิตภัณฑ์ที่มุ่งป้องกันระบบหรือข้อมูลเกี่ยวกับความมั่นคงแห่งชาติต้องได้การทบทวนและการรับรองจากสำนักงานความมั่นคงแห่งชาติ (NSA) ก่อนจัดหามาใช้[15]
เออีเอสตามมาตรฐานต้องคำนวณเข้ารหัส 10 รอบสำหรับกุญแจขนาด 128 บิต, 12 รอบสำหรับกุญแจ 192 บิต และ 14 รอบสำหรับกุญแจ 256 บิต จนถึงปี 2006 วิธีการโจมตีทางทฤษฎีซึ่งจัดว่าดีที่สุดและตีพิมพ์เป็นผลงาน ใช้โจมตีเออีเอสที่มีกุญแจ 128 บิตและคำนวณเข้ารหัส 7 รอบ, กุญแจ 192 บิตที่คำนวณ 8 รอบ และกุญแจ 256 บิตที่คำนวณ 9 รอบ[16]
วิธีการโจมตีที่รู้
[แก้]สำหรับนักวิทยาการเข้ารหัสลับ การทอน (break) การเข้ารหัสลับก็คือปฏิบัติการโจมตีที่ทำได้เร็วกว่าการใช้กำลังล้วน ๆ ซึ่งเป็นการลองถอดรหัสด้วยกุญแจที่อาจจะใช่เป็นลำดับ ดังนั้น การทอนจึงรวมวิธีที่จริง ๆ ยังทำไม่ได้ด้วยเทคโนโลยีปัจจุบัน ซึ่งแม้จะปฏิบัติไม่ได้ แต่ก็ช่วยให้เข้าใจรูปแบบของความอ่อนแอ การโจมตีด้วยกำลังล้วน ๆ ซึ่งได้ผลที่สุด ปรากฏต่อสาธารณชน ทำต่อขั้นตอนวิธีการเข้ารหัสลับแบบบล็อกไซเฟอร์[D]ซึ่งได้ทำให้เกิดผลอย่างกว้างขวางที่สุด เป็นการโจมตีกุญแจ RC5 ขนาด 64 บิต โดย distributed.net[R] ในปี 2006[17]
ขนาดของกุญแจเท่ากับเพิ่มเป็นสองเท่าต่อบิตทุกบิตที่เพิ่มในกุญแจ และถ้ากุญแจอาจมีค่าอะไรก็ได้ในโอกาสเท่า ๆ กัน การโจมตีด้วยกำลังล้วน ๆ เพื่อหากุญแจเท่ากับต้องเพิ่มเวลาเป็นสองเท่าโดยเฉลี่ย ซึ่งเท่ากับต้องเพิ่มเวลาเป็นเลขชี้กำลังตามขนาดกุญแจ แต่ขนาดกุญแจเพียงอย่างเดียวไม่ได้แน่นอนว่าปลอดภัยเพราะก็มีไซเฟอร์[E]ที่มีกุญแจใหญ่มากแต่พบว่าอ่อนแอ
เออีเอสใช้หลักพีชคณิตที่ค่อนข้างง่าย[18] ในปี 2002 นักวิทยาการเข้ารหัสชาวอังกฤษและออสเตรเลียได้แสดงการโจมตีโดยทฤษฎีซึ่งเรียกว่า XSL attack เพื่อแสดงจุดอ่อนของขั้นตอนวิธีเออีเอส โดยส่วนหนึ่งก็เพราะความซับซ้อนไม่มากของการคำนวณแบบไม่ใช่เชิงเส้นของมัน[19] แต่ต่อมานักวิชาการอื่น ๆ ก็ได้แสดงว่า การโจมตีที่กล่าวนี้ทำให้ได้ผลไม่ได้
ในช่วงการเลือกไซเฟอร์เพื่อเป็นมาตรฐานเออีเอส ผู้พัฒนาวิธีคู่แข่งได้เขียนถึงขั้นตอนวิธีเรนดาลไว้ว่า "...พวกผมเป็นห่วงเรื่องการใช้ (ไซเฟอร์นี้) ... ในโปรแกรมประยุกต์ที่ความปลอดภัยสำคัญขีดสุด"[20] แต่ในปลายปี 2000 หลังจากได้ตั้งเออีเอสแล้ว ผู้พัฒนาขั้นตอนวิธีคู่แข่งคือ Twofish ได้เขียนว่า แม้เขาคิดว่า วันหนึ่งจะเกิดการโจมตีเชิงวิชาการ (คือโดยทฤษฎีที่นำไปใช้จริง ๆ ไม่ได้ด้วยเทคโนโลยีปัจจุบัน) ต่อเรนดาลที่ได้ผล แต่เขา "ไม่เชื่อว่า จะมีใครค้นพบการโจมตีที่ทำให้สามารถอ่านการสื่อสารที่เข้ารหัสโดยเรนดาลได้"[21]
ในปี 2009 มีการค้นพบ related-key attack[C] (การโจมตีโดยมีกุญแจสัมพันธ์) แบบหนึ่งที่ถือเอาประโยชน์จากความเรียบง่ายของ AES key schedule[J] โดยมีความซับซ้อนที่ 2119 ซึ่งเมื่อถึงปลายปีได้ทำให้เร็วขึ้นเหลือ 299.5[2] แต่ related-key attack ก็ไม่เป็นปัญหาในเกณฑ์วิธีการเข้ารหัสลับที่ออกแบบและทำให้เกิดผลอย่างเหมาะสม เพราะโปรแกรมย่อมไม่ยอมให้ใช้กุญแจที่สัมพันธ์กัน
ในปี 2009 นักวิชาการได้ตีพิมพ์ (เป็นเอกสารที่ยังไม่ได้ทบทวนโดยผู้รู้เสมอกัน) การโจมตีเออีเอส-256 โดยใช้กุญแจที่สัมพันธ์กันเพียงแค่ 2 ตัว ใช้การคำนวณซับซ้อนระดับ 239 เพื่อเจาะกุญแจขนาด 256 บิตเมื่อคำนวณเข้ารหัสเพียงแค่ 9 รอบ หรือ 245 เมื่อคำนวณเข้ารหัส 10 รอบโดยใช้การโจมตีแบบ related subkey attack ที่กุญแจสัมพันธ์กันยิ่งกว่า หรือ 270 เมื่อเจาะการเข้ารหัสที่คำนวณ 11 รอบ[22] แต่จริง ๆ เออีเอส 256 บิตต้องเข้ารหัส 14 รอบ การโจมตีเยี่ยงนี้จึงไม่ได้ผลต่อเออีเอสที่ใช้จริง ๆ การนำไปใช้ได้จริง ๆ ของการโจมตีที่มีกุญแจสัมพันธ์กันยิ่งกว่าก็ถูกวิจารณ์[23] แม้โดยวินเซ็นต์ เรเม็นเอง[24]
ในปลายปี 2009 มีการตีพิมพ์การโจมตีแบบ known-key distinguishing attack แรกต่อเออีเอส-128 ที่เข้ารหัส 8 รอบ[25] โดยมีความซับซ้อนเชิงเวลาที่ 248 และความซับซ้อนเชิงความจำที่ 232 แต่เพราะเออีเอส-128 ต้องเข้ารหัส 10 รอบ การโจมตีนี้จึงไม่มีผลต่อเออีเอสที่ใช้กันจริง ๆ
การโจมตีโดยกู้คืนกุญแจ (key-recovery attack) ต่อเออีเอสเต็ม ๆ ได้พิมพ์ในงานปี 2011[26] การโจมตีเป็นแบบ biclique attack และเร็วกว่าการโจมตีที่ใช้กำลังอย่างเดียวถึง 4 เท่า โดยต้องใช้การดำเนินการ 2126.2 ครั้งเพื่อกู้คืนกุญแจ AES-128 สำหรับ AES-192 และ AES-256 ต้องใช้การดำเนินการ 2190.2 และ 2254.6 ครั้งตามลำดับ ต่อมาผลจึงได้ทำเร็วขึ้นเป็น 2126.0 สำหรับ AES-128, 2189.9 สำหรับ AES-192 และ 2254.3 สำหรับ AES-256[27] เหล่านี้เป็นผลที่ได้ดีสุดสำหรับการโจมตีโดยกู้คืนกุญแจต่อเออีเอส
นี่เป็นประโยชน์เพียงเล็กน้อย เพราะกุญแจขนาด 126 บิต (แทนที่อาจใช้คือ 128 บิต) ยังต้องใช้เวลาเป็นพัน ๆ ล้านปีถ้าใช้ฮาร์ดแวร์ปัจจุบันหรือแบบที่ยังพอเล็งเห็นล่วงหน้าได้ อนึ่ง ผู้เขียนคำนวณว่า การโจมตีเร็วสุดโดยใช้เทคนิกของผู้เขียนต่อเออีเอสที่ใช้กุญแจ 128 บิตยังต้องเก็บข้อมูล 288 บิต เท่ากับข้อมูล 38 ล้านล้านเทระไบต์ ซึ่งมากกว่าข้อมูลที่เก็บบนคอมพ์ทั้งหมดในโลกในปี 2016 ดังนั้น นี่จึงไม่ทำลายความปลอดภัยของเออีเอส[28] ต่อมา ข้อมูลที่ต้องเก็บลดได้เหลือ 256 บิต[27] ซึ่งเท่ากับ 9,007 เทระไบต์
ตามข้อมูลรั่วของเอ็ดเวิร์ด สโนว์เดน สำนักงานความมั่นคงแห่งชาติสหรัฐ (NSA) กำลังวิจัยว่า การโจมตีการเข้ารหัสลับโดยใช้สถิติเทา (tau statistic) อาจช่วยเจาะเออีเอสได้หรือไม่[29]
ดังนั้นในปัจจุบัน จึงยังไม่มีการโจมตีที่ปฏิบัติได้ซึ่งช่วยให้บุคคลที่ไม่มีกุญแจสามารถอ่านข้อมูลที่เข้ารหัสลับด้วยเออีเอสเมื่อทำให้เกิดผลอย่างถูกต้อง
Side-channel attack
[แก้]side-channel attack[Q] เป็นการโจมตีไซเฟอร์แบบไม่ได้ทำต่อกล่องดำ ดังนั้น ไซเฟอร์ต่าง ๆ จึงไม่ได้ออกแบบต่อต้านการโจมตีเช่นนี้โดยตรง แต่ก็มีผลทางการปฏิบัติ คือ มันโจมตีการทำให้เกิดผลของไซเฟอร์ที่ฮาร์ดแวร์หรือซอฟต์แวร์มีข้อมูลรั่วไหลอย่างไม่ได้ตั้งใจ มีการโจมตีเช่นนี้หลายอย่างที่รู้สำหรับเออีเอส
ในกลางปี 2005 นักวิทยาการเข้ารหัสลับชาวเยอรมัน-อเมริกันประกาศการโจมตีอาศัยเวลาของแคช (cache-timing attack) ที่เขาใช้เจาะทำลายเซิร์ฟเวอร์ซึ่งทำตามสั่ง (custom server) และใช้การเข้ารหัสลับเออีอัสด้วยคลัง OpenSSL[30] โดยต้องใช้ข้อความธรรมดา 200 ล้านข้อความ[31] และเซิฟเวอร์ได้ตั้งให้รั่วข้อมูลเกี่ยวกับเวลาให้มากสุดเท่าที่จะเป็นไปได้ (คือ มันรายงานจำนวนไซเคิลที่ต้องใช้เพื่อเข้ารหัส) นักวิชาการผู้นี้ชี้ว่า "การลดความแม่นยำของตราเวลาเซิร์ฟเวอร์ หรือการกำจัดมันจากคำตอบสนองของเซิฟเวอร์ ไม่สามารถระงับการโจมตีได้ เพราะระบบลูกข่ายเพียงต้องจับเวลาไปกลับ (round-trip timing) ที่กำหนดด้วยนาฬิกาตนเอง แล้วชดเชยข้อมูลรบกวนที่มีเพิ่มขึ้นโดยสร้างค่าเฉลี่ยของตัวอย่างเป็นจำนวนเพิ่มขึ้น"[30]
ในปลายปี 2005 นักวิทยาการเข้ารหัสลับสามท่านตีพิมพ์เอกสารแสดงการโจมตีอาศัยเวลาของแคชต่อการทำเออีเอสให้เกิดผลที่พบใน OpenSSL และฟังกชันเข้ารหัสลับส่วนดิสก์ของลินุกซ์ คือ dm-crypt[32]
การโจมตีหนึ่งสามารถได้กุญแจเออีเอสหลังจากเพียงแค่การเข้ารหัสลับเพียง 800 ครั้งโดยใช้เวลาเพียงแค่ 65 มิลลิวินาที
แต่ผู้โจมตีก็จำเป็นต้องดำเนินงานโปรแกรมในระบบหรือแพล็ตฟอร์มที่เข้ารหัสเออีเอสได้
ในปลายปี 2009 มีการตีพิมพ์การโจมตีต่อการทำให้เกิดผลบนฮาร์ดแวร์โดยใช้การวิเคราะห์ความผิดพร่องต่าง (differential fault analysis)[S] ซึ่งทำให้สามารถกู้คืนกุญแจด้วยความซับซ้อน 232[33]
ในปลายปี 2010 นักวิชาการได้ตีพิมพ์เอกสารอธิบายวิธีการที่ทำได้เกือบในเวลาจริงเพื่อกู้คืนกุญแจลับจาก AES-128 โดยไม่จำเป็นต้องได้ข้อความธรรมดาหรือข้อความไซเฟอร์ เป็นการโจมตีที่ใช้ได้กับการทำเออีเอส-128 ให้เกิดผลที่ใช้ compression table เช่น OpenSSL[34] การโจมตีนี้ก็จำเป็นต้องดำเนินการโปรแกรมที่ไม่เป็นเอกสิทธิบนระบบที่เข้ารหัสลับเหมือนกัน ซึ่งอาจทำได้ด้วยมัลแวร์อันง่ายกว่าการเข้าถึงบัญชีผู้ดูแลระบบ (root account) มาก[35]
ในต้นปี 2016 นักวิชาการได้แสดง side-channel attack[Q] ที่มีประสิทธิภาพมากต่อการทำเออีเอสให้เกิดผลซึ่งสามารถกู้คืนกุญแจ 128 บิตทั้งหมดอาศัยเพียงแค่ข้อความธรรมดา/ข้อความไซเฟอร์เพียงแค่ 6-7 บล็อก นี่ดีขึ้นอย่างมากเทียบกับงานก่อน ๆ ที่ต้องอาศัยการเข้ารหัสลับระหว่าง 100-1,000,000 ครั้ง[36] แต่ก็ต้องสามารถดำเนินการโปรแกรมในระดับผู้ใช้เหมือนกันโดยดำเนินการขั้นตอนวิธีเก็บกุญแจเพียงไม่ถึงนาที
อย่างไรก็ดี ซีพียูปัจจุบันจำนวนมากมีชุดคำสั่งเออีเอสในฮาร์ดแวร์ (เช่น AES-NI) ซึ่งช่วยป้องกัน side-channel attack ที่อาศัยเวลาเช่นตามที่ว่า[37][38]
การตรวจรับรองของ NIST/CSEC
[แก้]สถาบันมาตรฐานและเทคโนโลยีแห่งชาติสหรัฐ (NIST) ร่วมกับสถาบันความปลอดภัยการสื่อสาร (CSE) ของรัฐบาลกลางแคนาดาดำเนินการโปรแกรม Cryptographic Module Validation Program (CMVP) ซึ่งตรวจรับรองมอดูลการเข้ารหัสลับ (cryptographic modules) ข้อมูลราชการรัฐบาลกลางสหรัฐที่อ่อนไหวแต่ไม่จัดว่าลับต้องเข้ารหัสลับด้วยมอดูลการเข้ารหัสลับที่ได้การตรวจรับรองตาม FIPS 140-2 (มาตรฐานการประมวลข้อมูลของรัฐบาลกลางสหรัฐ) ซึ่ง NIST เป็นผู้กำหนด คือ "ผลิตภัณฑ์การเข้ารหัสลับเพื่อป้องกันข้อมูลลับจะต้องรับรองโดยสำนักงานความมั่นคงแห่งชาติ (NSA) และผลิตภัณฑ์การเข้ารหัสลับที่หมายป้องกันข้อมูลที่อ่อนไหวจะต้องรับรองตาม FIPS 140-2 ของ NIST"[39]
รัฐบาลแคนาดายังแนะนำให้กระทรวงต่าง ๆ ของแคนาดาใช้มอดูลเข้ารหัสลับที่ได้ตรวจรับรองตาม FIPS 140 สำหรับข้อมูลที่ไม่จัดว่าลับ (unclassified)
แม้ FIPS 197 จะเป็นเอกสารที่เจาะจงขั้นตอนวิธีเออีเอสโดยเฉพาะ ผู้ขายสินค้ามักจะขอให้ CMVP ตรวจรับรองขั้นตอนวิธีหลายอย่างพร้อมกัน ๆ (เช่น Triple DES หรือ SHA1) ภายใต้ระเบียบของ FIPS 140 ดังนั้น จึงไม่ค่อยมีมอดูลเข้ารหัสลับที่ตรวจรับรองโดยเฉพาะเพียงของ FIPS 197 และองค์กร NIST เองก็ไม่ได้ระบุมอดูลที่ผ่านการตรวจรับรองแบบ FIPS 197 ในรายการเฉพาะตนเองบนเว็บไซต์ขององค์กร โดยทั่วไป มอดูลที่ผ่านการตรวจรับรองแบบ FIPS 197 จะระบุด้วยสัญกรณ์ "FIPS approved: AES" พร้อมกับหมายเลขรับรองภายในรายการมอดูลที่ผ่านการตรวจรับรองแบบ FIPS 140
ส่วนโปรแกรม Cryptographic Algorithm Validation Program (CAVP) ของ NIST เช่นกัน[40] อนุญาตให้องค์กรอื่น ๆ ตรวจความถูกต้องของการทำขั้นตอนวิธีเออีเอสให้เกิดผลโดยมีค่าใช้จ่ายน้อยกว่า[ต้องการอ้างอิง] มอดูลที่ได้ตรวจรับรองสำเร็จก็จะปรากฏเป็นรายการในเว็บเพจของ NIST เช่นกัน[41] การทดสอบตามที่ว่าต้องทำก่อนจะตรวจรับรองตามระเบียบ FIPS 140-2 ที่จะว่าต่อไป เพราะการรับรองของ CAVP ไม่ได้บ่งว่ามอดูลได้ทำขั้นตอนวิธีให้เกิดผลอย่างปลอดภัย ดังนั้น มอดูลที่ยังไม่ผ่านการตรวจรับรองแบบ FIPS 140-2 หรือการอนุมัติโดยเฉพาะจาก NSA จึงไม่จัดว่าปลอดภัยเพื่อใช้ป้องกันข้อมูลราชการของรัฐบาลกลางสหรัฐ[39]
การได้การรับรองตาม FIPS 140-2 ทำได้ยากทั้งโดยเทคนิกและโดยค่าใช้จ่าย[42] เพราะมีชุดการทดสอบมาตรฐานและมีการทบทวนรหัสคำสั่งที่ต้องผ่านภายในไม่กี่อาทิตย์ ค่าใช้จ่ายเพื่อทดสอบในแล็บที่อนุมัติอาจสูงมาก (เช่น มากกว่า 30,000 เหรียญสหรัฐ หรือประมาณ 9 แสนบาท)[42] ซึ่งยังไม่รวมเวลาที่ต้องใช้เขียนและตรวจสอบมอดูล ทำเอกสาร และเตรียมมอดูลเพื่อตรวจรับรอง หลังจากได้การรับรองแล้ว ยังต้องกลับทำอีกถ้ามอดูลเปลี่ยน ซึ่งอาจจะเป็นแค่การอัปเดตเอกสารง่าย ๆ เมื่อการเข้ารหัสลับไม่ได้เปลี่ยนไป หรืออาจจะต้องตรวจสอบใหม่ถ้าการเปลี่ยนแปลงมีผลต่อการเข้ารหัสลับ
เวกเตอร์การทดสอบ
[แก้]เวกเตอร์การทดสอบเป็นชุดข้อความไซเฟอร์บวกกับข้อความธรรมดาและกุญแจเข้ารหัส NIST เผยแพร่เวกเตอร์การทดสอบเป็นตัวชุดอิงที่เรียกว่า AES Known Answer Test (KAT) Vectors[T]
ความเร็ว
[แก้]การทำได้เร็วในเครื่องที่มีแรมน้อยเป็นเกณฑ์ในการเลือกไซเฟอร์เพื่อเป็นเออีเอส ซึ่งทำงานได้ดีในฮาร์ดแวร์หลายอย่างมากมาย เริ่มตั้งแต่สมาร์ตการ์ดขนาด 8 บิตไปจนถึงคอมพิวเตอร์กำลังแรงสูง
ในเครื่องเพนเทียมโปร การเข้ารหัสลับเออีเอสต้องใช้รอบซีพียู 18 รอบ (ไซเคิล) ต่อไบต์[43] ซึ่งเสมอกับปริมาณงาน (throughput) ประมาณ 11 เมกะบิตต่อวินาทีสำหรับซีพียู 200 เมกะเฮิรตซ์ สำหรับซีพียู Pentium M 1.7 กิกะเฮิรตซ์ ปริมาณงานอยู่ที่ 60 เมกะบิตต่อวินาที
สำหรับซีพียูอินเทล Core i3/i5/i7 และเอเอ็มดี Ryzen รุ่นที่สนับสนุนชุดคำสั่งเออีเอส (AES-NI instruction set) ปริมาณงานอาจเป็นหลายจิกะบิตต่อวินาที (มีแม้ที่มากกว่า 10 จิกะบิตต่อวินาที)[44]
การทำให้เกิดผล
[แก้]มีการทำเออีเอสให้เกิดผลในรูปแบบต่าง ๆ มากมายรวมทั้งคลังโปรแกรม โปรแกรมประยุกต์ต่าง ๆ และในฮาร์ดแวร์เอง
- คลังโปรแกรม
- โปรแกรมประยุกต์
- ฮาร์ดแวร์
- ซีพียูอินเทลและเอเอ็มดีที่สนับสนุนชุดคำสั่งเออีเอส (AES-NI)
- เมนเฟรมไอบีเอ็ม zSeries
- ซีพียู SPARC S3 ที่สนับสนุนชุดคำสั่งเออีเอส (AES-NI)
เชิงอรรถ
[แก้]- ↑ ขั้นตอนวิธีเรนดาลสนับสนุนกุญแจขนาด 128, 160, 192, 224 และ 256 บิต แต่ AES กำหนดขนาดกุญแจเพียง 3 ขนาดคือ 128, 192 และ 256 บิต
- ↑ ขั้นตอนวิธีเรนดาลสนับสนุนบล็อกขนาด 128, 160, 192, 224 และ 256 บิต แต่ AES กำหนดบล็อกเพียงขนาดเดียวคือ 128 บิต
- ↑ 3.0 3.1 ในวิทยาการเข้ารหัสลับ related-key attack เป็นการวิเคราะห์การเข้ารหัสลับ (cryptanalysis) ใดก็ได้ที่ผู้โจมตีสามารถเห็นการดำเนินการของการเข้ารหัสเมื่อใช้กุญแจต่าง ๆ หลายตัวที่ไม่รู้ค่ากุญแจในเบื้องต้น แต่รู้ความสัมพันธ์เชิงคณิตของกุญแจเหล่านั้น ยกตัวอย่าง เช่น ผู้โจมตีอาจรู้ว่า บิต 80 บิตสุดท้ายของกุญแจที่ว่าเหมือนกันแม้จะไม่รู้ในตอนแรกว่าบิต 80 บิตนี้มีค่าอะไร วิธีการโจมตีนี้ดูในเบื้องต้นว่าไม่สมจริง เพราะผู้โจมตีไม่น่าจะสามารถชักชวนให้ผู้เข้ารหัสที่เป็นมนุษย์เข้ารหัสข้อมูลด้วยกุญแจลับหลายตัวที่สัมพันธ์กัน
- ↑ 4.0 4.1 4.2 ในวิทยาการเข้ารหัสลับ บล็อกไซเฟอร์ (block cipher) เป็นขั้นตอนวิธีเชิงกำหนดที่ปฏิบัติการต่อบิตจำนวนตายตัว ซึ่งเรียกว่าบล็อก ด้วยการแปลงอันกำหนดด้วยกุญแจแบบสมมาตร (symmetric key) บล็อกไซเฟอร์เป็นองค์ประกอบพื้นฐานสำหรับเกณฑ์วิธีการเข้ารหัสลับหลายชนิด และใช้อย่างกว้างขวางเพื่อเข้ารหัสลับข้อมูลจำนวนมาก ๆ
- ↑ 5.0 5.1 5.2 ในวิทยาการเข้ารหัสลับ ไซเฟอร์ (cipher, cypher) เป็นขั้นตอนวิธีเพื่อเข้ารหัสลับหรือถอดรหัสลับ เป็นลำดับขั้นตอนที่ระบุอย่างละเอียดเพื่อให้ทำตามได้ คำภาษาอังกฤษอื่นที่ใช้ก็คือ encipherment คำว่า "to encipher" หรือ "to encode" หมายถึงการแปลงข้อมูลให้เป็นไซเฟอร์คือเป็นรหัสลับ
- ↑ ในวิทยาการเข้ารหัสลับ ไซเฟอร์ฟายสเติล (Feistel cipher) เป็นโครงสร้างสมมาตรที่ใช้สร้างบล็อกไซเฟอร์ เป็นชื่อตามนักฟิสิกส์และนักวิทยาการเข้ารหัสลับชาวเยอรมัน คือ ฮอร์สต์ ฟายสเตล ซึ่งได้ทำงานวิจัยรุ่นบุกเบิกที่บริษัทไอบีเอ็ม (สหรัฐ) ไซเฟอร์นี่มีชื่ออีกอย่างว่า เครือข่ายฟายสเตล บล็อกไซเฟอร์จำนวนมากใช้กลยุทธ์นี้ รวมทั้ง Data Encryption Standard (DES) มีข้อดีตรงที่ว่า การเข้ารหัสและการถอดรหัสคล้ายกันมาก ในบางกรณีเหมือนกันเลย เพียแต่ต้องใช้ key schedule กลับทางเท่านั้น ดังนั้น ขนาดคำสั่งหรือวงจรที่จำเป็นเพื่อทำให้เกิดผลจึงเหลือเกือบครึ่งเดียว เครือข่ายฟายสเตลเป็นไซเฟอร์แบบวนซ้ำ (iterated) ซึ่งมีฟังกชันที่เรียกว่า round function[10]
- ↑ ในวิทยาการคอมพิวเตอร์ row-major order (อันดับตามแถว) และ column-major order (อันดับตามสดมภ์) เป็นวิธีเก็บแถวลำดับหลายมิติ (multidimensional array) ในหน่วยเก็บเชิงเส้นเช่นแรม อันดับต่างกันตรงที่ว่าสมาชิกไหนของแถวลำดับจะเก็บต่อกันในความจำ สำหรับอันดับตามแถว สมาชิกติดกันของแถวจะเก็บต่อกัน เทียบกับอันดับตามสดมภ์ที่สมาชิกติดกันของสดมภ์จะเก็บต่อกัน
- ↑ รูปแปรของเรนดาลที่มีบล็อกใหญ่จะใช้แถวลำดับที่มีสดมภ์เพิ่มขึ้น แต่จะมีแถว 4 แถวเท่านั้น
- ↑ ในสาขาคณิตศาสตร์ คำว่า ฟิลด์จำกัด ภายในคำว่า เลขคณิตในฟิลด์จำกัด (finite field arithmetic) หมายถึงฟิลด์ที่มีสมาชิกจำนวนจำกัด (finite) นี่เทียบกับ เลขคณิตในฟิลด์อนันต์ (infinite) ที่ไม่จำกัดจำนวนสมาชิก เช่น ฟิลด์ของจำนวนตรรกยะ แม้จะไม่มีฟิลด์จำกัดที่เป็นอนันต์ แต่ก็มีฟิลด์จำกัดเป็นจำนวนอนันต์ จำนวนสมาชิกย่อมอยู่ในรูป pn โดย p เป็นจำนวนเฉพาะและ n เป็นจำนวนเต็มบวก และฟิลด์จำกัดที่มีขนาดเดียวกันย่อมเป็นสมสัณฐาน (isomorphic) กับกันและกัน จำนวนเฉพาะ p เรียกว่า characteristic of the field และจำนวนเต็มบวก n เรียกว่า dimension of the field over its prime field
- ↑ 10.0 10.1 10.2 เออีเอส (เรนดาล) ใช้ขั้นตอนวิธี key schedule เพื่อขยายกุญแจสั้นตัวหนึ่งเป็นกุญแจรอบที่ต่างกันจำนวนหนึ่ง นี่เป็นขั้นตอนที่เรียกว่า Rijndael key schedule รูปแปรของเออีเอสสามอย่างมีจำนวนรอบที่ต่างกัน รูปแปรแต่ละอย่างจะต้องมีกุญแจรอบขนาด 128 บิตสำหรับแต่ละรอบ บวกเพิ่มอีกหนึ่งตัว ขั้นตอนนี้ผลิตกุญแจรอบจำนวณตามที่จำเป็นโดยได้จากกุญแจสมมาตร
- ↑ Rijndael S-box เป็นเมทริกซ์จัตุรัสที่ใช้ในไซเฟอร์เรนดาล ซึ่งขั้นตอนวิธีเออีเอสเป็นอนุพันธ์ โดยใช้เป็นตารางค้นหา
- ↑ ในวิทยาการเข้ารหัสลับ S-box หรือ substitution box (กล่องการแทนที่) เป็นองค์ประกอบพื้นฐานของขั้นตอนวิธีการเข้ารหัสลับด้วยกุญแจสมมาตร เป็นองค์ประกอบที่ใช้สำหรับแทนที่ สำหรับบล็อกไซเฟอร์ นี้ทำเพื่อปิดบังความสัมพันธ์ระหว่างกุญแจกับข้อความไซเฟอร์ (เป็น Shannon's property of confusion) โดยทั่วไป S-box รับบิตอินพุตจำนวนหนึ่ง คือ m แล้วแปลงมันเป็นบิตเอาต์พุตอีกจำนวนหนึ่งคือ n ซึ่งไม่ต้องเท่ากับ m[11] S-box แบบ m×n สามารถทำให้เกิดผลโดยเป็นตารางค้นหาโดยมีคำ 2m แต่ละคำมีขนาด n บิต ปกติจะใช้ตารางตายตัว เช่น ใน Data Encryption Standard (DES) แต่ไซเฟอร์บางอย่างก็สร้างตารางอย่างไม่ตายตัวจากกุญแจ (เช่น ขั้นตอนวิธีการเข้ารหัสลับของ Blowfish และ Twofish)
- ↑ ในเรขาคณิต การแปลงสัมพรรค (affine transformation, affine map, affinity) (จากคำละตินว่า affinis แปลว่า เชื่อมต่อกับ) เป็นฟังก์ชันระหว่างปริภูมิสัมพรรค (affine spaces) ซึ่งคงสภาพจุด เส้นตรง และระนาบ อนึ่ง เซตของเส้นขนานก็จะคงขนานกันหลังการแปลง แต่การแปลงสัมพรรคอาจไม่คงสภาพมุมระหว่างเส้นหรือระยะทางระหว่างจุด แม้จะคงอัตราของระยะทางระหว่างจุดที่อยู่บนเส้นตรงเดียวกัน
- ↑ ในคณิตศาสตร์เชิงการจัด derangement เป็นการเรียงสับเปลี่ยนสมาชิกของเซตโดยไม่ให้สมาชิกอยู่ในตำแหน่งเดิม กล่าวอีกอย่างก็คือ derangement เป็นการเรียงสับเปลี่ยนที่ไร้จุดตรึง (fixed point)
- ↑ รูปแปรของเรนดาลที่มีบล็อกใหญ่กว่ามีระยะการเลื่อนที่ต่างกันบ้าง สำหรับบล็อกขนาด 128 และ 192 บิต วิธีการเลื่อนจะเหมือนกัน คือ แถว จะเลื่อนหมุนไปทางซ้ายเป็นจำนวน ช่อง/ไบต์ สำหรับบล็อกขนาด 256 บิต แถวแรกไม่เลื่อน แถวสอง สาม และสี่ จะเลื่อนไป 1, 3 และ 4 ไบต์ตามลำดับ โดยนี่ใช้กับไซเฟอร์เรนดาลเมื่อใช้บล็อกขนาด 256 บิต เทียบกับเออีเอสที่ไม่ใช้บล็อกขนาดนี้
- ↑ ในวิทยาการเข้ารหัสลับ confusion (ความสับสน) และ diffusion (ความแพร่) เป็นคุณสมบัติสองอย่างของปฏิบัติการไซเฟอร์ที่ปลอดภัย ดังที่ Claude Shannon ได้ระบุในรายงานราชการลับ A Mathematical Theory of Cryptography[12] คุณสมบัติเหล่านี้ช่วยป้องกันการเจาะวิเคราะห์การเข้ารหัสลับด้วยวิธีทางสถิติและวิธีอื่น ๆ แนวคิดเหล่านี้สำคัญในการออกแบบฟังก์ชันแฮชและฟังก์ชันสร้างเลขสุ่มเทียม (pseudorandom number) ที่ความไม่สัมพันธ์กันระหว่างค่าต่าง ๆ ที่สร้างเป็นเรื่องสำคัญอย่างยิ่งยวด
- ↑ 17.0 17.1 17.2 ในวิทยาการเข้ารหัสลับ side-channel attack หมายถึงการโจมตีใดก็ได้ที่ใช้ข้อมูลจากการทำให้เกิดผลบนเครื่องเข้ารหัสลับ แทนที่จะใช้กำลังล้วน ๆ (brute force) หรือที่จะหาจุดอ่อนทางทฤษฎีของขั้นตอนวิธีการเข้ารหัสลับ ยกตัวอย่างเช่น ข้อมูลเกี่ยวกับช่วงเวลา การใช้พลังงาน การรั่วไหลของรังสีแม่เหล็กไฟฟ้า หรือแม้แต่เสียงก็อาจให้ข้อมูลเพิ่มเพื่อถือโอกาสใช้เจาะทำลายระบบ
- ↑ distributed.net เป็นโครงการคอมพิวเตอร์แบบกระจาย (distributed computing) ที่พยายามแก้ปัญหาที่ต้องคำนวณมากโดยใช้ไซเคิลซีพียูหรือจีพียูที่ไม่งั้นแล้วก็เท่ากับอยู่เฉย ๆ เป็นโครงการที่บริหารโดยองค์การไม่แสวงหาผลกำไรสหรัฐ คือ Distributed Computing Technologies, Incorporated (DCTI)
- ↑ การวิเคราะห์ความผิดพร่องต่าง (differential fault analysis, DFA) เป็นการโจมตีแบบ side channel attack ในวิทยาการเข้ารหัสลับ หลักก็คือเหนี่ยวนำให้เกิดความผิดพร่อง (fault) คือภาวะสิ่งแวดล้อมที่ไม่ได้คาดหวัง ในการทำการเข้ารหัสลับให้เกิดผล เพื่อให้มันแสดงสถานะภายใน
- ↑ AES Known Answer Test (KAT) Vectors อยู่ในซิปไฟล์ที่เว็บไซต์ของ NIST คือ KAT_AES.zip หรือ เก็บถาวร 2009-10-23 ที่ เวย์แบ็กแมชชีน
อ้างอิง
[แก้]- ↑ "Biclique Cryptanalysis of the Full AES" (PDF). คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ มีนาคม 6, 2016. สืบค้นเมื่อ พฤษภาคม 1, 2019.
- ↑ 2.0 2.1 Biryukov, Alex; Khovratovich, Dmitry. "Related-key Cryptanalysis of the Full AES-192 and AES-256". International Association for Cryptologic Research. เก็บจากแหล่งเดิมเมื่อ 2009-09-28.
{{cite web}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ 3.0 3.1 Daemen, Joan; Rijmen, Vincent (March 9, 2003). "AES Proposal: Rijndael" (PDF). National Institute of Standards and Technology. p. 1. เก็บ (PDF)จากแหล่งเดิมเมื่อ 5 March 2013. สืบค้นเมื่อ 21 February 2013.
- ↑ 4.0 4.1 4.2 "Announcing the ADVANCED ENCRYPTION STANDARD (AES)" (PDF). Federal Information Processing Standards Publication 197. United States National Institute of Standards and Technology (NIST). November 26, 2001. เก็บ (PDF)จากแหล่งเดิมเมื่อ March 12, 2017. สืบค้นเมื่อ October 2, 2012.
- ↑ Joan Daemen and Vincent Rijmen (September 3, 1999). "AES Proposal: Rijndael" (PDF). คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ February 3, 2007.
- ↑ John Schwartz (October 3, 2000). "U.S. Selects a New Encryption Technique". New York Times. เก็บจากแหล่งเดิมเมื่อ March 28, 2017.
- ↑ Westlund, Harold B. (2002). "NIST reports measurable success of Advanced Encryption Standard". Journal of Research of the National Institute of Standards and Technology. คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2007-11-03.
- ↑ "ISO/IEC 18033-3: Information technology – Security techniques – Encryption algorithms – Part 3: Block ciphers". เก็บจากแหล่งเดิมเมื่อ 2013-12-03.
- ↑ Bruce Schneier; John Kelsey; Doug Whiting; David Wagner; Chris Hall; Niels Ferguson; Tadayoshi Kohno; และคณะ (May 2000). "The Twofish Team's Final Comments on AES Selection" (PDF). เก็บ (PDF)จากแหล่งเดิมเมื่อ 2010-01-02.
- ↑ Menezes, Alfred J.; van Oorschot, Paul C; Vanstone, Scott A (2001). Handbook of Applied Cryptography (5th ed.). p. 251. ISBN 0849385237.
{{cite book}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ Chandrasekaran, J.; และคณะ (2011). "A Chaos Based Approach for Improving Non Linearity in the S-Box Design of Symmetric Key Cryptosystems". ใน Meghanathan, N.; และคณะ (บ.ก.). Advances in Networks and Communications: First International Conference on Computer Science and Information Technology, CCSIT 2011, Bangalore, India, January 2-4, 2011. Part 2, p. 516. ISBN 978-3-642-17877-1.
- ↑ "Model Based Inference in the Life Sciences: A Primer on Evidence". 2008: 51–82. doi:10.1007/978-0-387-74075-1_3.
{{cite journal}}: Cite journal ต้องการ|journal=(help) - ↑ Bertoni, Guido; Breveglieri, Luca; Fragneto, Pasqualina; Macchetti, Marco; Marchesin, Stefano (2003). "Efficient software implementation of AES on 32-bit platforms" (PDF). Lecture Notes in Computer Science: 2523. Springer.
{{cite web}}: CS1 maint: uses authors parameter (ลิงก์)[ลิงก์เสีย] - ↑ "byte-oriented-aes – A public domain byte-oriented implementation of AES in C – Google Project Hosting". เก็บจากแหล่งเดิมเมื่อ 2013-07-20. สืบค้นเมื่อ 2012-12-23.
- ↑ Lynn Hathaway (June 2003). "National Policy on the Use of the Advanced Encryption Standard (AES) to Protect National Security Systems and National Security Information" (PDF). เก็บ (PDF)จากแหล่งเดิมเมื่อ 2010-11-06. สืบค้นเมื่อ 2011-02-15.
- ↑ John Kelsey, Stefan Lucks, Bruce Schneier, Mike Stay, David Wagner, and Doug Whiting, Improved Cryptanalysis of Rijndael, Fast Software Encryption, 2000 pp213–230 "Academic: Improved Cryptanalysis of Rijndael - Schneier on Security". เก็บจากแหล่งเดิมเมื่อ 2007-02-23. สืบค้นเมื่อ 2007-03-06.
- ↑ Ou, George (April 30, 2006). "Is encryption really crackable?". Ziff-Davis. เก็บจากแหล่งเดิมเมื่อ August 8, 2010. สืบค้นเมื่อ August 7, 2010.
- ↑ "Sean Murphy". University of London. เก็บจากแหล่งเดิมเมื่อ 2009-01-31. สืบค้นเมื่อ 2008-11-02.
- ↑ Bruce Schneier. "AES News, Crypto-Gram Newsletter, September 15, 2002". เก็บจากแหล่งเดิมเมื่อ 7 July 2007. สืบค้นเมื่อ 2007-07-27.
- ↑ Niels Ferguson; Richard Schroeppel; Doug Whiting (2001). "A simple algebraic representation of Rijndael". Proceedings of Selected Areas in Cryptography, 2001, Lecture Notes in Computer Science. Springer-Verlag. pp. 103–111. CiteSeerX 10.1.1.28.4921. คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF/PostScript)เมื่อ 4 November 2006. สืบค้นเมื่อ 2006-10-06.
- ↑ Bruce Schneier, AES Announced เก็บถาวร 2009-02-01 ที่ เวย์แบ็กแมชชีน, October 15, 2000
- ↑ Alex Biryukov; Orr Dunkelman; Nathan Keller; Dmitry Khovratovich; Adi Shamir (2009-08-19). "Key Recovery Attacks of Practical Complexity on AES Variants With Up To 10 Rounds". เก็บจากแหล่งเดิมเมื่อ 28 January 2010. สืบค้นเมื่อ 2010-03-11.
- ↑ Agren, Martin (2012). On Some Symmetric Lightweight Cryptographic Designs. Dissertation, Lund University. pp. 38–39.
- ↑ Vincent Rijmen (2010). "Practical-Titled Attack on AES-128 Using Chosen-Text Relations" (PDF). เก็บ (PDF)จากแหล่งเดิมเมื่อ 2010-07-02.
{{cite journal}}: Cite journal ต้องการ|journal=(help) - ↑ Henri Gilbert; Thomas Peyrin (2009-11-09). "Super-Sbox Cryptanalysis: Improved Attacks for AES-like permutations". เก็บจากแหล่งเดิมเมื่อ 2010-06-04. สืบค้นเมื่อ 2010-03-11.
- ↑ Andrey Bogdanov; Dmitry Khovratovich & Christian Rechberger (2011). "Biclique Cryptanalysis of the Full AES" (PDF). คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2012-09-05.
- ↑ 27.0 27.1 Biaoshuai Tao & Hongjun Wu (2015). Information Security and Privacy. Lecture Notes in Computer Science. Vol. 9144. pp. 39–56. doi:10.1007/978-3-319-19962-7_3. ISBN 978-3-319-19961-0.
- ↑ Jeffrey Goldberg (2011-08-18). "AES Encryption isn't Cracked". คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 8 January 2015. สืบค้นเมื่อ 30 December 2014.
- ↑ SPIEGEL ONLINE, Hamburg, Germany (28 December 2014). "Inside the NSA's War on Internet Security". SPIEGEL ONLINE. เก็บจากแหล่งเดิมเมื่อ 24 January 2015. สืบค้นเมื่อ 4 September 2015.
- ↑ 30.0 30.1 "Index of formal scientific papers". Cr.yp.to. เก็บจากแหล่งเดิมเมื่อ 2008-09-17. สืบค้นเมื่อ 2008-11-02.
- ↑ Bruce Schneier. "AES Timing Attack". เก็บจากแหล่งเดิมเมื่อ 12 February 2007. สืบค้นเมื่อ 2007-03-17.
- ↑ Dag Arne Osvik; Adi Shamir; Eran Tromer (2005-11-20). "Cache Attacks and Countermeasures: the Case of AES" (PDF). เก็บ (PDF)จากแหล่งเดิมเมื่อ 2006-06-19. สืบค้นเมื่อ 2008-11-02.
{{cite journal}}: Cite journal ต้องการ|journal=(help) - ↑ Dhiman Saha; Debdeep Mukhopadhyay; Dipanwita RoyChowdhury. "A Diagonal Fault Attack on the Advanced Encryption Standard" (PDF). เก็บ (PDF)จากแหล่งเดิมเมื่อ 22 December 2009. สืบค้นเมื่อ 2009-12-08.
{{cite journal}}: Cite journal ต้องการ|journal=(help) - ↑ Endre Bangerter; David Gullasch & Stephan Krenn (2010). "Cache Games – Bringing Access-Based Cache Attacks on AES to Practice" (PDF). เก็บ (PDF)จากแหล่งเดิมเมื่อ 2010-12-14.
{{cite journal}}: Cite journal ต้องการ|journal=(help) - ↑ "Breaking AES-128 in realtime, no ciphertext required". Hacker News. เก็บจากแหล่งเดิมเมื่อ 2011-10-03. สืบค้นเมื่อ 2012-12-23.
- ↑ Ashokkumar C.; Ravi Prakash Giri; Bernard Menezes (2016). 2016 IEEE European Symposium on Security and Privacy (EuroS&P). pp. 261–275. doi:10.1109/EuroSP.2016.29. ISBN 978-1-5090-1751-5. S2CID 11251391.
- ↑ "Are AES x86 Cache Timing Attacks Still Feasible?" (PDF). cseweb.ucsd.edu. เก็บ (PDF)จากแหล่งเดิมเมื่อ 2017-08-09.
- ↑ "Archived copy" (PDF). เก็บ (PDF)จากแหล่งเดิมเมื่อ 2013-03-31. สืบค้นเมื่อ 2017-07-26.
{{cite web}}: CS1 maint: archived copy as title (ลิงก์) Securing the Enterprise with Intel AES-NI. - ↑ 39.0 39.1 "Archived copy" (PDF). คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2012-04-21. สืบค้นเมื่อ 2012-05-29.
{{cite web}}: CS1 maint: archived copy as title (ลิงก์) - ↑ "NIST.gov – Computer Security Division – Computer Security Resource Center". Csrc.nist.gov. เก็บจากแหล่งเดิมเมื่อ 2013-01-02. สืบค้นเมื่อ 2012-12-23.
- ↑ "Validated FIPS 140-1 and FIPS 140-2 Cryptographic Modules". คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2014-12-26. สืบค้นเมื่อ 2014-06-26.
- ↑ 42.0 42.1 OpenSSL, openssl@openssl.org. "OpenSSL's Notes about FIPS certification". Openssl.org. คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2013-01-02. สืบค้นเมื่อ 2012-12-23.
- ↑ Schneier, Bruce; Kelsey, John; Whiting, Doug; Wagner, David; Hall, Chris; Ferguson, Niels (1999-02-01). "Performance Comparisons of the AES submissions" (PDF). เก็บ (PDF)จากแหล่งเดิมเมื่อ 2011-06-22. สืบค้นเมื่อ 2010-12-28.
- ↑ "AMD Ryzen 7 1700X Review".
- Courtois, Nicolas; Pieprzyk, Josef (2003). "Cryptanalysis of Block Ciphers with Overdefined Systems of Equations". ใน Zheng, Yuliang (บ.ก.). Advances in Cryptology – ASIACRYPT 2002: 8th International Conference on the Theory and Application of Cryptology and Information Security, Queenstown, New Zealand, December 1–5, 2002, Proceedings. Springer. pp. 268–287. ISBN 978-3-540-36178-7.
- Daemen, Joan; Rijmen, Vincent (2002). The Design of Rijndael: AES – The Advanced Encryption Standard. Springer. ISBN 978-3-540-42580-9.
- Paar, Christof; Pelzl, Jan (2009). Understanding Cryptography: A Textbook for Students and Practitioners. Springer. pp. 87–122. ISBN 978-3-642-04101-3. alternate link (companion web site contains online lectures on AES)
แหล่งข้อมูลอื่น
[แก้]- "256bit key — 128bit block — AES". Cryptography — 256 bit Ciphers: Reference source code and submissions to international cryptographic designs contests. EmbeddedSW.
- "Advanced Encryption Standard (AES)" (PDF). Federal Information Processing Standards. 2001-11-26. doi:10.6028/NIST.FIPS.197. 197.
- AES algorithm archive information - (old, unmaintained)
- "Part 3: Block ciphers" (PDF). Information technology — Security techniques — Encryption algorithms (2nd ed.). ISO. 2010-12-15. ISO/IEC 18033-3:2010(E).
- Animation of Rijndael - AES deeply explained and animated using Flash (by Enrique Zabala / University ORT / Montevideo / Uruguay). This animation (in English, Spanish, and German) is also part of CrypTool 1 (menu Indiv. Procedures -> Visualization of Algorithms -> AES).










