ทฤษฎีระบบควบคุม
บทความนี้ยังต้องการเพิ่มแหล่งอ้างอิงเพื่อพิสูจน์ความถูกต้อง |
ลิงก์ข้ามภาษาในบทความนี้ มีไว้ให้ผู้อ่านและผู้ร่วมแก้ไขบทความศึกษาเพิ่มเติมโดยสะดวก เนื่องจากวิกิพีเดียภาษาไทยยังไม่มีบทความดังกล่าว กระนั้น ควรรีบสร้างเป็นบทความโดยเร็วที่สุด |

- en:Control Systems|
- en:Control Systems]]มีหน้าในหัวข้อ [[wikibooks:th:
- en:Control Systems/ตำราทฤษฎีระบบควบคุม|ตำราทฤษฎีระบบควบคุม]]
ทฤษฎีระบบควบคุม (อังกฤษ: control theory) เป็นสาขาหนึ่งของคณิตศาสตร์และวิศวกรรมศาสตร์ ในที่นี้ การควบคุมหมายถึง การควบคุมระบบพลศาสตร์ ให้มีค่าเอาต์พุตที่ต้องการ โดยการป้อนค่าอินพุตที่เหมาะสมให้กับระบบ ตัวอย่างที่เห็นได้ทั่วไป เช่น ระบบควบคุมอุณหภูมิห้องของเครื่องปรับอากาศ หรือ แม้แต่ลูกลอยในโถส้วม ที่เปิดน้ำปิดน้ำโดยอัตโนมัติเมื่อน้ำหมดและน้ำเต็ม
การควบคุมการขับเคลื่อนยานพาหนะ เช่น รถยนต์ ก็ถือเป็นการควบคุมชนิดหนึ่ง โดยผู้ขับขี่เป็นผู้ควบคุมทิศทางและความเร็ว ซึ่งระบบควบคุมประเภทที่ต้องมีคนเข้ามาเกี่ยวข้องนี้ถือว่าเป็น ระบบควบคุมไม่อัตโนมัติ (manual control) แต่ทฤษฎีระบบควบคุมจะครอบคลุมเฉพาะการวิเคราะห์และออกแบบ ระบบควบคุมอัตโนมัติ (automatic control) เท่านั้น เช่น ระบบขับเคลื่อนอัตโนมัติ (cruise control)
ระบบควบคุมยังอาจแบ่งออกได้เป็นระบบควบคุมวงเปิด (open-loop control) คือ ระบบควบคุมที่ไม่ได้ใช้สัญญาณจากเอาต์พุต มาบ่งชี้ถึงลักษณะการควบคุม ส่วนระบบควบคุมวงปิด (closed-loop control) หรือ ระบบป้อนกลับ (feedback control) นั้นจะใช้ค่าที่วัดจากเอาต์พุต มาคำนวณค่าการควบคุม นอกจากนี้ยังอาจแบ่งได้ตามคุณลักษณะของระบบ เช่น เป็นเชิงเส้น (linear) / ไม่เป็นเชิงเส้น (nonlinear) , แปรเปลี่ยนตามเวลา (time-varying) / ไม่เปลี่ยนแปลงตามเวลา (time-invariant) และเวลาต่อเนื่อง (Continuous time) / เวลาไม่ต่อเนื่อง (Discontinuous time)
ประวัติศาสตร์และการพัฒนาของทฤษฎีระบบควบคุม[แก้]
ระบบควบคุมในยุคโบราณ[แก้]
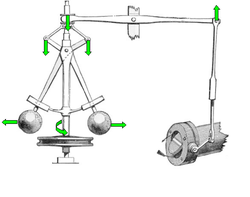
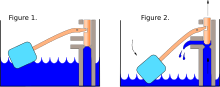
การใช้ระบบควบคุมวงปิด นั้นมีมาแต่โบราณกาล ตัวอย่างเช่น นาฬิกาน้ำของกรีก ซึ่งมีการใช้ลูกลอยในการควบคุมระดับน้ำในถัง อุปกรณ์ที่ถือว่าเป็นจุดเริ่มต้น ของการใช้ระบบควบคุมป้อนกลับในวงการอุตสาหกรรม ก็คือ ลูกเหวี่ยงหนีศูนย์กลาง (centrifugal governor หรือเรียก fly-ball governor) ในการควบคุมความเร็วในการหมุน เครื่องจักรไอน้ำที่ประดิษฐ์ขึ้นโดย เจมส์ วัตต์ ในปี ค.ศ. 1788
จุดกำเนิดของทฤษฎีระบบควบคุม[แก้]
- แบบจำลองคณิตศาสตร์ของระบบควบคุม
ในยุคก่อนหน้านี้ การออกแบบระบบควบคุมต่าง ๆ นั้น เป็นไปในลักษณะลองผิดลองถูก ไม่ได้มีการใช้คณิตศาสตร์ในการวิเคราะห์ ออกแบบแต่อย่างใด จนกระทั่งในปี ค.ศ. 1840 นักดาราศาสตร์ชาวอังกฤษ จอร์จ แอรี ได้ประดิษฐ์อุปกรณ์ควบคุมทิศทางของกล้องดูดาว โดยอุปกรณ์นี้จะหมุนกล้องดูดาว เพื่อชดเชยกับการหมุนของโลกโดยอัตโนมัติ ในระหว่างการออกแบบ แอรีได้สังเกตถึงความไม่เสถียร (instability) ของระบบป้อนกลับ จึงใช้สมการเชิงอนุพันธ์ในการจำลองและวิเคราะห์พฤติกรรมของระบบ การวิเคราะห์เสถียรภาพของระบบนี้เป็นหัวใจสำคัญของทฤษฎีระบบควบคุม
- ทฤษฎีเสถียรภาพ
ในปี ค.ศ. 1868 เจมส์ เคลิร์ก แมกซ์เวลล์ เป็นบุคคลแรก ที่ทำการศึกษาถึงเสถียรภาพของ ลูกเหวี่ยงหนีศูนย์กลางของ เจมส์ วัตต์ โดยใช้แบบจำลองสมการเชิงอนุพันธ์เชิงเส้น ทฤษฎีเสถียรภาพของระบบเชิงเส้นของแมกซ์เวลล์นี้ พิจารณาเสถียรภาพของระบบจาก รากของสมการคุณลักษณะ (characteristic equation) ของระบบ ต่อมาในปี ค.ศ. 1892 เลียปูนอฟได้ทำการศึกษาถึงเสถียรภาพของระบบไม่เป็นเขิงเส้น และสร้างทฤษฎีเสถียรภาพของเลียปูนอฟ (Lyapunov stability) แต่ทฤษฎีของเลียปูนอฟนี้เป็นทฤษฎีที่สำคัญที่ไม่ได้รับความสนใจ จนกระทั่งหลายสิบปีต่อมา
ระบบควบคุมแบบดั้งเดิม[แก้]
- ระบบควบคุมแบบดั้งเดิม (อังกฤษ: classical control) หมายถึง ระบบควบคุมที่ออกแบบและวิเคราะห์บนโดเมนความถี่ (หรือโดเมนการแปลงฟูรีเย) และโดเมนการแปลงลาปลาส โดยการใช้แบบจำลองในรูปของ ฟังก์ชันส่งผ่าน (transfer function) โดยไม่ได้ใช้ข้อมูลรายละเอียดของไดนามิกส์ภายในของระบบ (internal system dynamic)
พัฒนาการของทฤษฎีระบบควบคุมในช่วงนี้นั้น ส่วนใหญ่พัฒนาขึ้นเพื่อประยุกต์ใช้งานในทางทหารและทางระบบสื่อสาร อันเนื่องมาจากสงครามโลกครั้งที่สอง และ การขยายตัวของโครงข่ายสื่อสารโทรศัพท์
- พัฒนาการเพื่อใช้งานในระบบโครงข่ายโทรศัพท์
ในช่วงยุคที่มีการขยายตัวของระบบสื่อสารโทรศัพท์นั้น ระบบสื่อสารทางไกลมีความจำเป็นต้องใช้อุปกรณ์ขยายสัญญาณด้วยหลอดสุญญากาศ ในปี ค.ศ. 1927 แนวความคิดและประโยชน์ของระบบป้อนกลับแบบลบ ได้ถูกนำเสนอในรูปของ อุปกรณ์ขยายสัญญาณป้อนกลับแบบลบ (negative feedback amplifier) โดย เอช. เอส. แบล็ก แต่การวิเคราะห์เสถียรภาพของระบบขยายสัญญาณตามทฤษฎีของแมกซ์เวลล์ โดยใช้วิธีของ เราท์-ฮิวรวิทซ์ (Routh-Hurwitz) นั้นเป็นไปได้ยาก เนื่องจากความซับซ้อนของระบบ วิศวกรสื่อสารของ Bell Telephone Laboratories จึงได้นำเสนอการวิเคราะห์บนโดเมนความถี่ โดยในปี ค.ศ. 1932 แฮร์รี่ ไนควิสต์นำเสนอ เกณฑ์เสถียรภาพของไนควิสต์ (Nyquist stability criterion) ซึ่งใช้วิธีการพล็อตกราฟเชิงขั้ว ของผลตอบสนองความถี่ตลอดวงรอบ (loop frequency response) ของระบบ ต่อมาในปี ค.ศ. 1940 เฮนดริค โบดีได้นำเสนอวิธีการวิเคราะห์เสถียรภาพโดยขอบเขตอัตราขยาย (gain margin) และขอบเขตมุม (phase margin) จากกราฟระหว่างขนาดและมุม (phase) ของผลตอบสนองความถี่ เรียกว่า โบดีพล็อต (Bode plot)
- พัฒนาการเพื่อการใช้งานทางด้านการทหาร
ปัญหาหลายปํญหาในทางหทาร เช่น ปัญหาการนำร่องการเดินเรืออัตโนมัติ ปัญหาการเล็งเป้าโดยอัตโนมัติ นั้นเป็นแรงผลักดันสำคัญให้เกิดการพัฒนาการทางทฤษฎีระบบควบคุมที่สำคัญหลายอย่าง ในปี ค.ศ. 1922 มินอร์สกี (N. Minorsky) ได้กำหนดและวิเคราะห์กฎของ ระบบควบคุมพีไอดี หรือ สัดส่วน-ปริพันธ์-อนุพันธ์ (proportional-integral-derivative) ซึ่งยังเป็นที่นิยมใช้อย่างกว้างขวางในปัจจุบัน เพื่อใช้ในการนำร่องการเดินเรือ ปัญหาที่สำคัญในช่วงนั้นคือ การเล็งเป้าของปืนจากเรือหรือเครื่องบิน ซึ่งในปี ค.ศ. 1934 ฮาเซน (H.L. Házen) ได้บัญญัติคำสำหรับประเภทปัญหาการควบคุมกลไกนี้ว่า กลไกเซอร์โว (servomechanisms) การวิเคราะห์และออกแบบนั้นก็ใช้วิธีการบนโดเมนความถี่ จนกระทั่งในปีค.ศ. 1948 อีแวนส์ (W. R. Evans) ซึ่งทำงานกับปัญหาทางด้านการนำร่องและควบคุมเส้นทางบิน ซึ่งส่วนใหญ่นั้นเป็นระบบที่ไม่เสถียร ได้ประสบกับปํญหาการวิเคราะห์เสถียรภาพบนโดเมนของความถี่ จึงได้หันกลับไปศึกษาถึงรากของสมการคุณลักษณะ ซึ่งเป็นวิธีการวิเคราะห์บนโดเมนการแปลงลาปลาส และได้พัฒนาวิธี ทางเดินราก (root locus) ในการออกแบบระบบ
ระบบควบคุมสมัยใหม่[แก้]


ระบบควบคุมสมัยใหม่ (อังกฤษ: modern control) หมายถึง ระบบควบคุมที่ไม่ได้ใช้เทคนิคในการออกแบบแบบดั้งเดิม คือ จากรากของสมการคุณลักษณะ และอยู่บนโดเมนความถี่ แต่เป็นการออกแบบ โดยมีพื้นฐานจากแบบจำลองสมการอนุพันธ์ของไดนามิกส์ของระบบ และเป็นการออกแบบอยู่บนโดเมนเวลา
แรงผลักดันของพัฒนาการจากระบบควบคุมแบบดั้งเดิม มาสู่ระบบควบคุมสมัยใหม่นี้ มีอยู่หลัก ๆ สองประการคือ
ข้อจำกัดของระบบควบคุมแบบดั้งเดิมต่องานด้านอวกาศยาน : จากความสำเร็จในการส่งดาวเทียมสปุตนิก 1 ของสหภาพโซเวียตในปี ค.ศ. 1957 นั้นกระตุ้นให้เกิดความตื่นตัวของการประยุกต์ใช้งานทางด้านอวกาศยาน ความสำเร็จของโซเวียตนั้นเนื่องมาจากพัฒนาการทางด้านทฤษฎีระบบควบคุมแบบไม่เป็นเชิงเส้น ซึ่งไม่ได้รับความสนใจมากนักจากประเทศตะวันตก เนื่องจากความล้มเหลวในการใช้เทคนิคต่าง ๆ ของระบบควบคุมแบบดั้งเดิม กับงานด้านอวกาศยาน ซึ่งระบบส่วนใหญ่นั้น เป็นระบบหลายตัวแปรแบบไม่เป็นเชิงเส้น (nonlinear multivariable system) จึงมีการหันกลับมาพิจารณาการวิเคราะห์จากปัญหาดั้งเดิม ในรูปของแบบจำลองสมการอนุพันธ์ของระบบ
การประยุกต์ใช้คอมพิวเตอร์กับงานระบบควบคุม :
พัฒนาการของคอมพิวเตอร์ มีส่วนสำคัญในการพัฒนาทฤษฎีต่าง ๆ ของระบบควบคุม เนื่องจากทำให้สามารถสร้างอุปกรณ์ควบคุมที่สามารถทำงานซับซ้อนได้ รวมทั้งการใช้คอมพิวเตอร์ช่วยคำนวณในการออกแบบกฎของการควบคุม ดังนั้นจึงมีการพัฒนาระบบควบคุมแบบต่าง ๆ ขึ้นอย่างมากมาย
ด้วยเหตุดังกล่าว จึงมีการพัฒนาทฤษฎีระบบควบคุม จากหลายแง่มุม
จากความพยายามในการใช้คอมพิวเตอร์ซึ่งเป็นดิจิทัล เพื่อการควบคุมระบบซึ่งโดยส่วนใหญ่จะเป็นระบบอนาล็อก จึงส่งผลให้มีการพัฒนาทางทฤษฎีระบบควบคุมดิจิทัล (อังกฤษ: digital control) โดยในปี ค.ศ. 1952 จอห์น รากัซซินี (J.R. Ragazzini) , แฟรงคลิน (G Franklin) และ ซาเดห์ (L.A. Zadeh ผู้คิดค้นฟัซซี่ลอจิก) ที่มหาวิทยาลัยโคลัมเบีย ได้พัฒนาทฤษฎีระบบแบบชักข้อมูล (sampled data systems) ขึ้น การใช้คอมพิวเตอร์ในการควบคุมกระบวนการในอุตสาหกรรมนั้น ครั้งแรกในปี ค.ศ. 1959 ที่ โรงกลั่นน้ำมัน พอร์ต อาเธอร์ (Port Arthur) ในรัฐเท็กซัส
นอกจากนั้นแล้วแนวความคิดของการควบคุมที่ซับซ้อนขึ้นโดยมีการรวม ข้อกำหนดความต้องการทางด้านประสิทธิภาพ (performance) ในการออกแบบระบบควบคุม ซึ่งเรียกว่า ระบบควบคุมแบบเหมาะสมที่สุด (optimal control) รากฐานของทฤษฎีระบบควบคุมแบบเหมาะสมที่สุดนี้มีมายาวนานตั้งแต่ปี ค.ศ. 1696 จาก หลักของความเหมาะสมที่สุด (principle of optimality) ในปัญหา บราคิสโตโครน (Brachistochrone curve) และ แคลคูลัสของการแปรผัน (Calculus of variations) ในปีค.ศ. 1957 ริชาร์ด เบลแมน ได้ประยุกต์ใช้วิธีการกำหนดการพลวัตของเขาในการแก้ปัญหาระบบควบคุมแบบเหมาะสมที่สุด แบบเวลาไม่ต่อเนื่อง ต่อมาในปีค.ศ. 1958 พอนเทรียกิน (L.S. Pontryagin) ได้พัฒนา หลักการมากที่สุด (maximum principle หรือบางครั้งก็เรียก minimum principle) สำหรับแก้ปัญหาในรูปของแคลคูลัสของการแปรผัน แบบเวลาต่อเนื่อง

การสังเกตถึงผลกระทบของสัญญาณรบกวนต่อประสิทธิภาพของระบบควบคุมนั้นมีมาตั้งแต่ในช่วงระบบควบคุมยุคดั้งเดิม เช่นในช่วงสงครามโลกครั้งที่สอง ในการพัฒนาระบบควบคุมสำหรับเรดาร์ติดเครื่องบิน เพื่อควบคุมการยิง ที่ ห้องทดลองเรดิเอชัน (Radiation Lab) ที่ เอ็มไอที, ฮอลล์ (A.C. Hall) ได้ประสบปัญหาในการออกแบบ เขาได้สังเกตถึงผลกระทบจากการออกแบบที่ไม่ได้คำนึงถึงสัญญาณรบกวนต่อประสิทธิภาพของระบบ ถึงแม้ว่าจะมีการคำนึงถึงผลกระทบของสัญญาณรบกวน แต่ก็ไม่ได้มีการใช้แบบจำลองทางคณิตศาสตร์ของสัญญาณรบกวนในการวิเคราะห์แต่อย่างใด จนกระทั่ง นอร์เบิร์ต วีนเนอร์ ได้จำลองสัญญาณรบกวน โดยใช้แบบจำลองกระบวนการสตอแคสติก หรือ แบบจำลองทางสถิติ แบบเวลาต่อเนื่อง ในการพัฒนาระบบเล็งเป้าและควบคุมการยิงปืนต่อต้านอากาศยาน โดยใช้ข้อมูลจากเรดาร์ ซึ่งงานของเขาได้ถูกเก็บเป็นความลับ จนถึงปี ค.ศ. 1949 ในช่วงเดียวกันในปี ค.ศ. 1941 คอลโมโกรอฟ ก็ได้ทำการพัฒนาแบบจำลองสำหรับระบบเวลาไม่ต่อเนื่องขึ้น ระบบควบคุมที่ใช้แบบจำลองสคอแคสติกนี้ในการวิเคราะห์ จะเรียกว่า ระบบควบคุมสตอแคสติก (Stochastic control)
การวิเคราะห์และควบคุมระบบบนโดเมนเวลา โดยใช้แบบจำลองตัวแปรสถานะ หรือ แบบจำลองปริภูมิสถานะ (state space) นั้นเป็นหัวใจของทฤษฎีระบบควบคุมสมัยใหม่ รูดอล์ฟ อีมิว คาลมาน และ Bellman นั้นถือได้ว่าเป็นบุคคลที่มีส่วนสำคัญในการพัฒนาทฤษฎีระบบควบคุมโดยใช้แบบจำลองตัวแปรสถานะนี้ โดยที่ในปี ค.ศ. 1960 คาลมานได้นำทฤษฎีเสถียรภาพของเลียปูนอฟมาใช้ในการออกแบบระบบ ซึ่งเป็นผลให้ผลงานของเลียปูนอฟกลับมาได้รับความสนใจ นอกจากนี้แนวทางใหม่นี้ยังสามารถตอบคำถามเกี่ยวกับลักษณะเฉพาะของตัวระบบได้ ได้แก่ สภาพควบคุมได้ (controllability) สภาพสังเกตได้ (observability) ผลสัมฤทธิ์เล็กสุดเฉพาะกลุ่ม (minimal realization) และยังนำไปสู่การออกแบบตัวควบคุมแบบใหม่ เช่น การวางขั้ว (pole placement) ตัวควบคุมอิงตัวสังเกต (observer-based controller) และตัวควบคุมกำลังสองเชิงเส้นเหมาะที่สุด (optimal linear quadratic regulator) [1] [2]คาลมานได้พัฒนาวิธีการออกแบบระบบควบคุมแบบเหมาะสมที่สุด จากแบบจำลองปริภูมิสถานะ ในรูปของปัญหาระบบเชิงเส้นคงค่าแบบเหมาะสมที่สุดตามสมการกำลังสอง หรือ LQR (linear quadratic regulator) ในปีเดียวกันนี้ คาลมานได้นำเสนอผลงานของเขาในการประยุกต์ใช้แบบจำลองตัวแปรสถานะนี้เข้ากับแนวความคิดทางด้านสตอแคสติกของวีนเนอร์ และคิดค้นสิ่งที่เรารู้จักกันในชื่อ ตัวกรองคาลมาน (Kalman filter) ขึ้นมา โดยการใช้งานจริงครั้งแรกของตัวกรองคาลมาน นั้นได้ถูกประยุกต์เป็นส่วนหนึ่งของระบบนำร่องในโครงการอพอลโล ตั้งแต่นั้นมาตัวกรองคาลมานก็ได้ถูกประยุกต์ใช้งานอย่างกว้างขวางในปัจจุบัน
ในปัจจุบันแนวทางการวิเคราะห์และควบคุมระบบบนโดเมนเวลา โดยใช้แบบจำลองตัวแปรสถานะสามารถประยุกต์ใช้ได้กับงานวิศวกรรมห้วงอากาศอวกาศ (aerospace engineering) การควบคุมกระบวนการ (process control) และเศษฐมิติ (econometrics) [1]
ประเภทของปัญหาระบบควบคุม[แก้]
ปัญหาของทฤษฎีระบบควบคุมนั้น สามารถแยกออกได้เป็นประเภทใหญ่ 2 ประเภท คือ
- ปัญหาระบบคงค่า (regulator problem) คือ ปัญหาที่มีจุดประสงค์ของการควบคุม ให้เอาต์พุตของระบบมีค่าคงที่ ต้านทานการรบกวน (disturbance) ที่เข้ามาในระบบ และมีผลทำให้ระบบเปลี่ยนแปลง
- ปัญหาระบบปรับค่าตาม (tracking หรือ servo problem) คือ ปัญหาที่มีจุดประสงค์ของการควบคุม ให้เอาต์พุตมีค่าเท่ากับสัญญาณอ้างอิง เมื่อสัญญาณอ้างอิงเปลี่ยนไป ระบบควบคุมจะทำการปรับให้ สัญญาณเอาต์พุตมีค่าตามสัญญาณอ้างอิง
ประเภทของระบบ[แก้]
เราอาจจะสามารถจำแนกประเภทของระบบได้หลายแบบตามแต่เงื่อนไขในการจำแนกระบบที่ใช้ แต่ในบริบทของทฤษฎีระบบควบคุมนั้น เรามักจำแนกระบบตามภาวะเชิงเส้น, การแปรเปลี่ยนตามเวลา และความต่อเนื่องโดเมนเวลา ดังต่อไปนี้ คือ
จำแนกตามภาวะเชิงเส้น[แก้]
ระบบเชิงเส้น[แก้]
ระบบเชิงเส้น (Linear Systems) คือระบบที่มีภาวะเชิงเส้น (Linearity) กล่าวคือ ถ้าให้ เป็นสัญญาณขาเข้าของระบบ และ โดยที่ เป็นสัญญาณขาออก ถ้าระบบมีภาวะเชิงเส้นแล้วจะต้องสอดคล้องกับคุณสมบัติดังนี้
หมายเหตุ: เราเรียกหลักการข้างต้นว่าหลักการซ้อนทับ (superposition)
ระบบไม่เชิงเส้น[แก้]
ระบบไม่เชิงเส้น (Nonlinear Systems) คือระบบที่ไม่มีสมบัติภาวะเชิงเส้นดังกล่าว
จำแนกตามการแปรเปลี่ยนตามเวลา[แก้]
ระบบไม่แปรเปลี่ยนตามเวลา[แก้]
ระบบไม่แปรเปลี่ยนตามเวลา (Time-invariant system) คือระบบที่คุณสมบัติของระบบไม่เปลี่ยนไปเมื่อเวลาเปลี่ยนไป กล่าวคือ สมมุติว่าไม่มีความล่าช้าเกิดขึ้นในระบบ (ระบบรับสัญญาณขาเข้าแล้วสามารถให้สัญญาณขาออกได้ในทันที) ถ้าป้อนสัญญาณขาเข้า ที่เวลา จะได้สัญญาณขาออกเป็น ที่เวลา ดังนั้นหากป้อนสัญญาณขาเข้าเดิมที่เวลา นั้นคือ สัญญาญาณขาออกผลลัพธ์ก็ต้องเป็น ค่าเดิม คือ เพียงแต่จะปรากฏที่เวลา ตามเวลาที่ป้อนสัญญาณขาเข้า
ระบบแปรเปลี่ยนตามเวลา[แก้]
ระบบแปรเปลี่ยนตามเวลา (Time-variant system) คือระบบที่จะปลี่ยนแปลงคุณสมบัติไปตามเวลา กล่าวคือ ถ้าป้อนสัญญาณขาเข้า ที่เวลา แล้วจะได้สัญญาณขาออกเป็น ที่เวลา ดังนั้นหากป้อนสัญญาณขาเข้าเดิมที่เวลา นั้นคือ สัญญาณขาออกผลลัพธ์ จะไม่ได้ค่าเดิม คือ แต่จะเป็นค่าอื่นเพราะในช่วงเวลา นั้นระบบได้เปลี่ยนคุณสมบัติไปแล้ว
จำแนกตามความต่อเนื่องโดเมนเวลา[แก้]
ระบบเวลาต่อเนื่อง[แก้]
ระบบเวลาต่อเนื่อง (Continuous time systems) คือระบบที่มีโดเมนเวลาเป็นสมาชิกเซตของจำนวนจริง กล่าวคือ
ระบบเวลาวิยุต[แก้]
ระบบเวลาวิยุต หรือ ระบบเวลาไม่ต่อเนื่อง (Discontinuous time systems) คือระบบที่มีโดเมนเวลาเป็นสมาชิกเซตของจำนวนเต็ม (แม้ในบางครั้ง อาจจะไม่ใช้จำนวนเต็ม แต่ ถ้ากล่าวโดยไม่เสียนัยยะความเป็นทั่วไป เราสามารถแทนจำนวนเหล่านั้นที่แม้ไม่ใช้จำนวนเต็มได้ด้วย ดัชนีเวลา (time index) ที่เป็นจำนวนเต็มได้เสมอ) กล่าวคือ
:หมายเหตุ เรามักจะใช้อักษร หรือ แทน ในกรณีที่เป็นเวลาวิยุต
ระบบผสม[แก้]
ระบบผสม (Hybrid systems) คือระบบที่โดเมนของเวลาต่อเนื่องเป็นช่วง ๆ กล่าวคือ มีทั้งช่วงที่ต่อเนื่องและไม่ต่อเนื่องในโดเมนของเวลา ตัวอย่างของระบบที่ศึกษากันคือ ระบบเชิงเส้นกระโดดแบบมาร์คอฟ (Markovian jump linear system : MJLS) [3] [4] [5] [6]
ในกรณีที่เป็น ระบบเชิงเส้นกระโดดแบบมาร์คอฟและเวลาไม่ต่อเนื่อง ระบบจะมีแบบจำลองดังต่อไปนี้
- โดยที่
เป็นตัวแปรสถานะของกระบวนการมาร์คอฟ (Markov process) ที่มีความน่าจะเป็นในการเปลี่ยนสถานะเป็น และเมทริกซ์ของระบบแปรเปลี่ยนขึ้นกับ
เป็นสัญญาณรบกวนที่มีต่อตัวระบบ
เป็นสัญญาณรบกวนที่มีการสังเกต (สัญญาณขาออก)
ส่วน จะนิยามในส่วนของแบบจำลองปริภูมิสถานะ ต่อไป
ทฤษฎีระบบควบคุมแบบดั้งเดิม[แก้]
ระบบควบคุมวงปิด[แก้]
เนื่องจากระบบควบคุมแบบวงเปิดมีปัญหาด้านเสถียรภาพของระบบเพราะไม่มีการป้อนกลับของสัญญาณขาออก ซึ่งไม่เหมาะกับการใช้งานหลายอย่าง จึงมีความต้องการที่จะออกแบบระบบควบคุมที่สามารถตรวจจับความคลาด
เคลื่อนระหว่างสัญญาณขาออกและสัญญาณอ้างอิงได้ จึงได้มีการคิดค้นระบบควบคุมแบบป้อนกลับ (Feedback control systems) หรือระบบควบคุมแบบวงปิด (Closed loop control systems) ขึ้นมาเพื่อหลีกเลี่ยงปัญหาที่เกิด
ขึ้นกับระบบควบคุมแบบวงเปิด โดยมีโครงสร้างดังในรูป
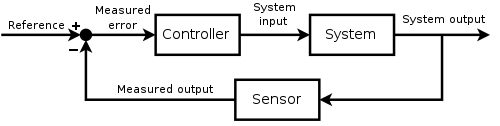
ระบบควบคุมแบบป้อนกลับมีความได้เปรียบเหนือกว่าระบบควบคุมแบบวงเปิด ดังต่อไปนี้
- สามารถกำจัดการรบกวนได้ (อาทิ เช่น ผลจากแรงเสียดทานที่ไม่ได้รวมอยู่ในแบบจำลองทางคณิตศาสตร์ของระบบ)
- สามารถรับประกันสมรรถนะได้มากขึ้นแม้กับแบบจำลองทางคณิตศาสตร์ที่มีตัวแปรที่มีความไม่แน่นอนอยู่ด้วย (อาทิ เช่น กรณีที่ผลจากการที่แบบจำลองทางคณิตศาสตร์ไม่สามารถอธิบายระบบได้อย่างสมบรูณแบบ)
- ระบบที่ไม่มีเสถียรภาพโดยธรรมชาติอยู่แล้วสามารถทำให้มีเสถียรภาพได้หากติดตั้งตัวควบคุมที่เหมาะสม
- ระบบมีความคงทนต่อความเปลี่ยนแปลงมากขึ้นแม้ในกรณีที่พารามิเตอร์ของระบบมีการเปลี่ยนแปลง
- ระบบสามารถปรับค่าสัญญาณขาออกตามสัญญาณอ้างอิงได้ดีมากขึ้นในปัญหาระบบปรับค่าตาม
ในบางระบบ ระบบควบคุมแบบวงปิดและวงเปิดจะใช้ควบคู่กัน โดยที่ในกรณีนี้ระบบวงเปิดจะเรียกว่า feedforward
ฟังก์ชันส่งผ่านของระบบวงปิด[แก้]

ฟังก์ชันส่งผ่าน (transfer function) คือความสัมพันธ์ทางคณิตศาสตร์ที่ใช้แสดงถึงความสัมพันธ์ระหว่างสัญญาณขาออก (output signal) ต่อสัญญาณขาเข้า (input signal) โดยฟังก์ชันส่งผ่านสามารถหาได้จากความสัมพันธ์ดังต่อไปนี้ สมมุติให้ ตัวควบคุม , ระบบพลวัต , ตัวตรวจจับ เป็นเชิงเส้น และ ไม่เปลี่ยนแปลงตามเวลา (ฟังก์ชันส่งผ่านของ , , and ไม่เปลี่ยนแปลงตามเวลา) และในที่นี้เราจะพิจารณาผลการแปลงการแปลงลาปลาสของฟังก์ชันส่งผ่านย่อย ๆ กล่าวคือ ฟังก์ชันส่งผ่านของ , , and ซึ่งการหาฟังก์ชันส่งผ่านหาได้ดังนี้
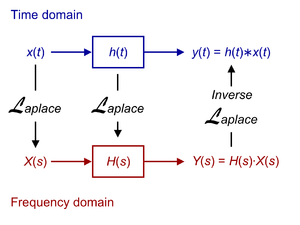
แก้หา ในรูปของ จะได้ว่า:
โดยที่ เราจะเรียกว่า ฟังก์ชันส่งผ่านของระบบวงปิดของระบบ (closed-loop transfer function)
ตัวควบคุมพีไอดี[แก้]

ตัวควบคุมพีไอดี หรือ ตัวควบคุมแบบสัดส่วน-ปริพันธ์-อนุพันธ์ เป็นตัวควบคุมที่ได้รับความนิยมเป็นอย่างสูงและใช้งานอย่างแพร่หลาย โดยในปัจจุบันยังมีการใช้งานในแวดวงอุตสาหกรรม จนไปถึงยานอวกาศ ทั้งนี้เพราะเป็นตัวคบคุมที่มีใช้งานกันมานานและจนได้รับความไว้วางในแง่ของประสิทธิภาพ อีกทั้งแบบจำลองทางคณิตศาสตร์ของมันก็เรียบง่ายและง่ายต่อการนำไปติดตั้ง ตัวควบคุมพีไอดีมีแบบจำลองทางคณิตศาสตร์ดังต่อไปนี้
กำหนดให้ คือสัญญาณควบคุมที่จะส่งให้ตัวระบบ
และ คือสัญญาณขาออกที่ถูกวัดมาได้
และ คือสัญญาณอ้างอิง
สัญญาณความคลาดเคลื่อนคือ ดังนั้น
สมรรถนะและเสถียรถาพของระบบจะถูกกำหนดโดยการปรับแต่งค่าพารามิเตอร์สามตัว คือ , และ นอกเหนือจากการปรับแต่งค่าเหล่านี้หลังจากการวิเคราะห์ทางคณิตศาสตร์ของตัวระบบแล้ว ในทางปฏิบัติ ยังนิยมปรับแต่งค่าโดยใช้หลักการของ Ziegler–Nichols หรือใช้ประสบการณ์ของวิศวกร โดยที่เสถียรภาพของระบบมักขึ้นอยู่กับพารามิเตอร์ แต่เพียงอย่างเดียว ส่วน มักส่งผลในแง่ของความคงทนต่อการเปลี่ยนแปลงฉับพลันต่อตัวระบบ และ มักเกี่ยวกับรูปร่างของผลตอบสนอง เมื่อพิจารณาบนโดเมนการแปลงลาปลาส จะได้ว่า
โดยจะเห็นได้ว่าฟังกชั่นส่งผ่านของตัวควบคุมพีไอดีคือ
แม้ระบบควบคุมแบบดั้งเดิมที่ใช้ตัวควบคุมพีไอดีจะมีความสามารถที่ถูกปรับปรุงดีขึ้นมากกว่าระบบควบคุมแบบเปิดมาก แต่ก็ยังเหมาะแค่กับระบบที่มีสัญญาณเข้าทางเดียวและสัญญาณขาออกทางเดียว (Single-Input and Single-Output or SISO) และยังไม่สามารถใช้ควบคุมระบบที่มีความซับซ้อนสูงได้ โดยเฉพาะอย่างยิ่งระบบที่มีสัญญาณขาเข้าหลายทางและสัญญาณขาออกหลายทาง (Multiple-Input and Multiple-Output or MIMO)
ทฤษฎีระบบควบคุมสมัยใหม่[แก้]
ระบบพลวัตส่วนใหญ่มักมีพฤติกรรมที่สามารถใช้สมการอนุพันธ์อันดับใด ๆ มาอธิบายได้ ในขณะเดียวกันสมการเชิงอนุพันธ์อันดับใด ๆ ก็สามารถลดอันดับให้เหลือเพียงสมการเชิงอนุพันธ์อันดับหนึ่งได้ จากความจริงตรงนี้จึงได้มีการเสนอวิธีการใหม่ในการวิเคราะห์และควบคุมระบบ ซึ่งจะวิเคราะห์บนโดเมนเวลาและได้มีการนำแบบจำลองปริภูมิสถานะ (state space) มาใช้ซึ่งจะอยู่ในรูปของสมการอนุพันธ์อันดับหนึ่งและแตกต่างจากระบบควบคุมแบบดั้งเดิมที่นิยมวิเคราะห์พฤติกรรมของระบบบนโดเมนความถี่ นอกจากนี้การนำแบบจำลองปริภูมิสถานะมาใช้ทำให้เราสามารถสร้างแบบจำลองทางคณิตศาสตร์สำหรับระบบแบบสัญญาณขาเข้าหลายทางสัญญาณขาออกหลายทาง (MIMO) ได้โดยการกำหนดมิติของตัวแปรในสมการปริภูมิสถานะอย่างเหมาะสม
แบบจำลองปริภูมิสถานะ(state space)[แก้]
กรณีระบบเชิงเส้น[แก้]
กำหนดให้ระบบพลวัตมี สัญญาณขาเข้า สัญญาณขาออก และ ตัวแปรสถานะ
สมการปริภูมิสถานะคือ:
โดยที่:
- คือ เวกเตอร์ของตัวแปรสถานะ (state vector) , ;
- คือ เวกเตอร์ของสัญญาณขาออก (output vector) , ;
- คือ เวกเตอร์ของสัญญาณขาเข้า หรือ เวกเตอร์ของสัญญาณควบคุม (input vector, control vector) , ;
- คือ เมทริกซ์ของตัวแปรสถานะ หรือ เมทริกซ์พลวัต (state matrix, dynamics matrix) , ,
- คือ เมทริกซ์ขาเข้า (input matrix) , ,
- คือ เมทริกซ์ขาออก (output matrix) , ,
- คือ เมทริกซ์ป้อนผ่าน (feedthrough (or feedforward) matrix) (ในกรณีที่ระบบไม่มีการป้อนสัญญาณขาเข้า, เป็นเมทริกซ์ศูนย์), ,
- .
โดยทั่วไปแล้ว เมทริกซ์ข้างต้นจะเป็นเมทริกซ์แปรผันตามเวลาได้ แต่ในกรณีเฉพาะที่ระบบไม่แปรผันตามเวลา (LTI) มักจะถูกนำมาศึกษาอยางแพร่หลายเพราะมีความซับซ้อนน้อยกว่าและเหมาะต่อการศึกษาในระดับพื้นฐาน นอกจากนี้ตัวแปรเวลาสามารถมีได้ทั้งแบบเวลาต่อเนื่อง (continuous time : ) และแบบเวลาวิยุต (ไม่ต่อเนื่อง) (discrete time : ) โดยในกรณีของเวลาไม่ต่อเนื่องมักนิยมใช้ตัวแปร นอกเหนื่อจากระบบแบบที่กล่าวมาแล้วยังมีระบบผสมซึ่งเป็นระบบที่มีโดเมนของเวลาอยู่ทั้งบนแกนเวลาต่อเนื่องและไม่ต่อเนื่อง
สมการปริภูมิสถานะ(state space equation)ข้างต้นหากพิจารณาตามโดเมนของเวลาจะมีรูปแบบต่าง ๆ กันดังต่อไปนี้ :
| ชนิดของระบบ | แบบจำลองสมการปริภูมิสถานะ |
| เวลาต่อเนื่องและไม่เปลี่ยนแปรตามเวลา (Continuous time-invariant) | |
| เวลาต่อเนื่องและเปลี่ยนแปรตามเวลา (Continuous time-variant) | |
| เวลาไม่ต่อเนื่องและไม่เปลี่ยนแปรตามเวลา (Explicit discrete time-invariant) | |
| เวลาไม่ต่อเนื่องและเปลี่ยนแปรตามเวลา (Explicit discrete time-variant) | |
| โดเมนการแปลงการแปลงลาปลาส โดยที่เวลาต่อเนื่องและไม่เปลี่ยนแปรตามเวลา (Laplace domain of continuous time-invariant) |
|
| โดเมน Z โดยที่เวลาไม่ต่อเนื่องและไม่เปลี่ยนแปรตามเวลา (Z-domain of discrete time-invariant) |
กรณีระบบไม่เชิงเส้น[แก้]
สภาพควบคุมได้[แก้]
สภาพควบคุมได้ (อังกฤษ: Controllability) จะบ่งบอกถึงความสามารถที่สัญญาณขาเข้าที่เป็นไปได้ (admissible inputs) จะสามารถขับเคลื่อนตัวแปรสถานะให้ไปถึงค่าใด ๆ ได้ในช่วงเวลาจำกัด (เวลาอันตะ) ไม่ว่าค่าเริ่มต้น (initial value) ของตัวแปรสถานะนั้น ๆ จะเป็นค่าอะไร ในกรณีระบบพลวัตเชิงเส้นเวลาต่อเนื่องไม่แปรผันตามเวลานั้นเงื่อนไขที่จะทำให้มีสภาพควบคุมได้ ก็ต่อเมื่อ
หมายเหตุ : ค่าลำดับขั้น (Rank) คือ ค่าซึ่งแสดงถึงจำนวนแถว (หรือหลัก) ในเมทริกซ์ที่มีความอิสระเชิงเส้น (linearly independent) ต่อกัน
สภาพสังเกตได้[แก้]
สภาพสังเกตได้ (อังกฤษ: Observability) เป็นสภาพที่บ่งบอกว่าระบบพลวัตมีความสามารถที่จะส่งผ่านข้อมูลของตัวแปรสถานะได้ดีแค่ไหนเมื่อพิจารณาจากสัญญาณขาออก สภาพควบคุมได้ และ สภาพสังเกตได้ เป็นสภาพคู่กันทางคณิตศาสตร์ (Duality) กล่าวคือ ในขณะที่ สภาพควบคุมได้ หมายถึง สภาพที่แสดงออกว่าสัญญาณขาเข้าสามารถขับเคลื่อนตัวแปรสถานะไปที่ค่าใด ๆ ที่ต้องการได้ แต่ สภาพสังเกตได้ จะเป็นสภาพที่แสดงออกถึงสัญญาณขาออก (output trajectory) จะให้ข้อมูลเพียงพอต่อการคาดคะเนค่าเริ่มต้นของตัวแปรสถานะของระบบได้ ในกรณีระบบพลวัตเชิงเส้นเวลาต่อเนื่องไม่แปรผันตามเวลานั้น เงื่อนไขที่จะทำให้มีสภาพสังเกตได้ได้ ก็ต่อเมื่อ
การแยกตัวประกอบคาลมาน[7][แก้]
การแยกตัวประกอบคาลมาน (อังกฤษ: Kalman decomposition) เป็นกระบวนการแยกส่วนประกอบของเมทริกซ์ในสมการปริภูมิสถานะของระบบเชิงเส้นไม่เปลี่ยนตามเวลา linear time-invariant (LTI) ให้อยู่ในรูปแบบที่สามารถจำแนกได้ว่าส่วนใดในเมทริกซ์ของระบบ มีผลต่อ สภาพสังเกตได้ และสภาพควบคุมได้ ทำให้ง่ายต่อการวิเคราะห์คุณลักษณะของระบบ
จากสมการปริภูมิสถานะของระบบข้างต้น จะเห็นได้ว่าพารามิเตอร์ที่กำหนดลักษณะของระบบ LTI สามารถเขียนโดยย่อได้เป็นเวกเตอร์ ในที่นี้จะสมมุติว่าระบบมีมิติเป็น .
การแยกตัวประกอบคาลมาน ถูกนิยามว่า คือ การแปลงเวกเตอร์ ให้เป็น โดยคูณเมทริกซ์การแปลง ดังต่อไปนี้
โดยเมทริกซ์การแปลง มีมิติ เป็นเมทริกซ์ผกผันได้ ถูกนิยามดังต่อไปนี้ ดังต่อไปนี้:
โดยที่
- เป็นเมทริกซ์ที่หลัก span ปริภูมิย่อย ของตัวแปรสถานะที่มีสถาพเข้าถึงได้ (reachable) และ ไม่มีสภาพสังเกตได้ (unobservable)
- ถูกเลือกโดยที่หลักของ เป็นฐานหลักของปริภูมิย่อยที่มีสภาพเข้าถึงได้ (reachable)
- ถูกเลือกโดยที่หลักของ เป็นฐานหลักของปริภูมิย่อยที่ไม่มีสภาพสังเกตได้ (unobservable)
- ถูกเลือกโดยที่ ยังสามารถผกผันได้
จะเห็นได้ว่าโดยการสร้งเมทริกซ์ ในลักษณะข้างต้น เมทริกซ์ จึงผกผันได้ เป็นที่น่าสังเกตว่าเมทริกซ์ย่อยในเมทริกซ์ นั้นสามารถเป็นเมทริกซ์ศูนย์ได้ ยกตัวอย่างเช่น กรณีที่ระบบมีสภาพสังเกตได้และควบคุมได้ เมทริกซ์ ลดรูปเหลือ โดยที่ เมทริกซ์ย่อยอื่นเป็นเมทริกซ์ศูนย์
รูปแบบมาตรฐาน[แก้]
ระบบที่ได้รับการแปลงแล้ว จะมีรูปแบบดังต่อไปนี้:
โดยที่
- ระบบย่อย มี สภาพเข้าถึงได้ และ สภาพสังเกตได้
- ระบบย่อย มี สภาพเข้าถึงได้
- ระบบย่อย มี สภาพสังเกตได้
บุคคลสำคัญในวงการทฤษฎีระบบควบคุม[แก้]
- อเล็กซานเดอร์ มิคาอิลโลวิช เลียปูนอฟ (ค.ศ. 1857 – ค.ศ. 1918) ในคริสต์ทศวรรษ 1890 นำเสนอเรื่องทฤษฎีเสถียรภาพของเลียปูนอฟ (Lyapunov stability) ซึ่งใช้วิเคราะห์ได้ทั้งระบบเชิงเส้นและไม่เชิงเส้นและเป็นทฤษฎีเสถียรภาพหลักในแขนงวิชาระบบควบคุมที่ยังใช้กันจนถึงถูกวันนี้
- แฮโรลด์ สตีเฟน แบล็ก (ค.ศ. 1898 – ค.ศ. 1983), นำเสนอแนวคิดเรื่องการป้อนกลับแบบลบ (negative feedback amplifiers) ในปี ค.ศ. 1927 และพัฒนาตัวขยายสัญญาณป้อนกลับแบบลบที่เสถียร์ได้สำเร็จในคริสต์ทศวรรษ 1930
- แฮร์รี่ ไนควิสต์ (ค.ศ. 1889 – ค.ศ. 1976) นำเสนอเกณฑ์เสถียรภาพของไนควิสต์ (Nyquist stability criterion) ในปี ค.ศ. 1932
- ริชาร์ด เบลแมน (Richard Bellman) (ค.ศ. 1920 – ค.ศ. 1984) ได้ประยุกต์ใช้วิธีการ กำหนดการพลวัตของเขา ในการแก้ปัญหาระบบควบคุมแบบเหมาะสมที่สุด แบบเวลาไม่ต่อเนื่อง ในปี ค.ศ. 1957
- อันเดรย์ คอลโมโกรอฟ (ค.ศ. 1903 – ค.ศ. 1987) พัฒนา Wiener-Kolmogorov filter ในปี ค.ศ. 1941 (ช่วงเวลาเดียวกับนอร์เบิร์ต วีนเนอร์)
- นอร์เบิร์ต วีนเนอร์ (Norbert Wiener) (ค.ศ. 1894 – ค.ศ. 1964) พัฒนา Wiener-Kolmogorov filter และนำเสนอศัพท์คำว่า cybernetics ในคริสต์ทศวรรษ 1940
- จอห์น อาร์ รากัซซินี (ค.ศ. 1912 – ค.ศ. 1988) นำเสนอระบบควบคุมแบบดิจิทัล และการแปลง z (z-transform) ในคริสต์ทศวรรษ 1950
- เลฟ พอนเทรียกิน (L.S. Pontryagin) (ค.ศ. 1908 – ค.ศ. 1988) หลักการมากที่สุด (maximum principle หรือบางครั้งก็เรียก minimum principle) สำหรับแก้ปัญหาในรูปของแคลคูลัสของการแปรผัน แบบเวลาต่อเนื่อง หลักการ แบง-แบง (bang-bang principle)
- รูดอล์ฟ อีมิว คาลมาน (ค.ศ. 1930 – ปัจจุบัน) ผู้พัฒนาตัวกรองคานมานและเป็นผู้นำเสนอแบบจำลองปริภูมิสถานะ และนำเสนอแนวคิดเรื่องสภาพควบคุมได้และสภาพสังเกตได้ มาใช้ในการสร้างแบบจำลองทางคณิตศาสตร์ของระบบ อันเป็นการนำองค์ความรู้ของทฤษฎีระบบควบคุมไปสู่ยุคใหม่ ที่เรียกว่า ทฤษฎีระบบควบคุมสมัยใหม่
สาขาของทฤษฎีระบบควบคุม[แก้]
- ระบบควบคุมเชิงเส้น (linear control systems)
- ระบบควบคุมไม่เป็นเชิงเส้น (nonlinear control systems)
- ระบบควบคุมดิจิทัล (digital control systems)
- ระบบควบคุมแบบเหมาะสมที่สุด (optimal control systems)
- ระบบควบคุมสตอแคสติค (stochastic control systems)
- ระบบควบคุมแบบคงทน (robust control systems)
- ระบบควบคุมแบบปรับตัวได้ (adaptive control systems)
- ระบบควบคุมแบบชาญฉลาด (intelligent control systems)
ดูเพิ่ม[แก้]
อ้างอิง[แก้]
- ↑ 1.0 1.1 เดวิด บรรเจิดพงศ์ชัย, "ระบบควบคุมพลวัต การวิเคราะห์ การออกแบบ และการประยุกต์ (Dynamical Control Systems Analysis, Design and Applications) " สำนักพิมพ์แห่งจุฬาลงกรณ์มหาวิทยาลัย 2551 (ISBN 978-974-03-2205-4)
- ↑ A New Approach to Linear Filtering and Prediction Problems, by R. E. Kalman, 1960
- ↑ Yuguang Fang, Kenneth A. Loparo, Stabilization of Continuous-Time Jump Linear, IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 47, NO. 10, OCTOBER 2002 page 1590-1603
- ↑ Yuguang, Kenneth A. Loparo, Xiangbo Feng, Stability of Discrete Time Jump Linear Systems, Journal of Mathematical Systems, Estimation, and Control, Vol 5, No. 3, pp. 275-321
- ↑ Vijay Gupta, Richard M. Murray, Ling Shi, Bruno Sinopoli Networked Sensing, Estimation and Control Systems
- ↑ "Vijay Gupta, Richard M. Murray Lecture Summary: Markov Jump Linear Systems" (PDF). คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2009-09-04. สืบค้นเมื่อ 2011-09-24.
- ↑ Lectures on Dynamic Systems and Control, Lecture 25[ลิงก์เสีย] - Mohammed Dahleh, Munther Dahleh, George Verghese — MIT OpenCourseWare
แหล่งข้อมูลอื่น[แก้]
- สื่อการสอนเกี่ยวกับทฤษฎีระบบควบคุม เก็บถาวร 2007-05-22 ที่ เวย์แบ็กแมชชีน ของ มหาวิทยาลัยคาร์เนกีเมลลอน
- หนังสือ Robust Adaptive Control เก็บถาวร 2009-08-23 ที่ เวย์แบ็กแมชชีน โดย Petros A. Ioannou
- Franklin, G.F., Powel, J.D., and Emami-Naeini, A. Feedback Control of Dynamic Systems, 4thed., Prentice Hall 2002 เก็บถาวร 2004-08-03 ที่ เวย์แบ็กแมชชีน
- Aström, K.J. Control System Design chap.1 preprint 2002
- Lewis, F.L. Applied Optimal Control and Estimation Prentice Hall 1992
- Bellman, R. "Eye of The Hurricane: an autobiography" World Scientific Publishing Co Pte Ltd. 1984
- A New Approach to Linear Filtering and Prediction Problems, by R. E. Kalman, 1960
- Katsuhiko Ogata, Modern control engineering (Edition 5), Prentice Hall, 2010, ISBN 0136156738,9780136156734
- M.W. Spong and M. Vidyasagar. Dynamics and Control of Root Manipulators. John Wiley, 1989
- เดวิด บรรเจิดพงศ์ชัย, ภาควิชาวิศวกรรมไฟฟ้า คณะวิศวกรรมศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย "ระบบควบคุมพลวัต การวิเคราะห์ การออกแบบ และการประยุกต์ (Dynamical Control Systems Analysis, Design and Applications) " สำนักพิมพ์แห่งจุฬาลงกรณ์มหาวิทยาลัย 2551 (ISBN 978-974-03-2205-4)
- วิบูลย์ แสงวีระพันธุ์ศิริ, ภาควิชาวิศวกรรมเครื่องกล คณะวิศวกรรมศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย "การควบคุมระบบพลศาสตร์ (Control of Dynamic Systems) " สำนักพิมพ์แห่งจุฬาลงกรณ์มหาวิทยาลัย 2548 (ISBN 974-13-3393-5)
- Kansas State University Control Lab เก็บถาวร 2012-02-07 ที่ เวย์แบ็กแมชชีน
- MIT Lecture Note on Dynamic Systems and Control by Munther Dahleh, Mohammed Dahleh, and George Verghese เก็บถาวร 2011-08-05 ที่ เวย์แบ็กแมชชีน



























































![{\displaystyle \operatorname {dim} [A(\cdot )]=n\times n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdb067922e2d625e2d0aaab3b6e54239cdd4f759)

![{\displaystyle \operatorname {dim} [B(\cdot )]=n\times p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e273a2878042f414ada7b454096d2d66125257a6)

![{\displaystyle \operatorname {dim} [C(\cdot )]=q\times n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aa4ac576864f9f09ea580fb19bd480fd12a68be)

![{\displaystyle \operatorname {dim} [D(\cdot )]=q\times p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759072ec7232e15a1823aec56b668df529d57dee)










































