เพนดูลัมผกผัน

แบบจำลองทางคณิตศาสตร์ของเพนดูลัมผกผันสามารถประยุกต์ใช้กับระบบควบคุมการทรงตัวของพาหนะอย่าง เซกเวย์ (Segway)ได้

เพนดูลัมผกผัน (อังกฤษ: Inverted pendulum) เป็นปัญหาพื้นฐานที่ใช้ในการเรียนการสอนและในการสาธิตการประยุกต์ทฤษฎีระบบควบคุม เพนดูลัมผกผันเป็นระบบที่มีจุดสมดุลอยู่รอบแกนหมุนด้วยกันสองจุด ได้แก่จุดที่เพนดูลัมตั้งตรงอยู่ในแนวดิ่ง และจุดที่เพนดูลัมอยู่ทิ้งตัวลงในดิ่ง แต่จุดที่มีเสถียรภาพเมื่อไม่มีตัวควบคุมนั้นจะมีจุดเดียวคือ จุดที่แกนทิ้งตัวลงเท่านั้น ไม่ว่าเราจะปล่อยเพนดูลัมที่จุดใดก็ตาม เพนดูลัมจะตกลงสู่จุดนี้เสมอ การที่จะทำให้เพนดูลัมนี้สามารถตั้งตรงในแนวดิ่งได้นั้นขึ้นกับการใส่ตัวควบคุมที่เหมาะสมเข้าไปในระบบซึ่งมีได้หลากหลายวิธี และอีกทั้งยังสามารถออกแบบตัวควบคุมให้เป็นเชิงเส้น หรือแบบไม่เชิงเส้นก็ได้ ทั้งนี้ขึ้นอยู่กับความต้องการของผู้ออกแบบและความเหมะสม

แบบจำลองทางคณิตศาสตร์ของเพนดูลัมผกผัน

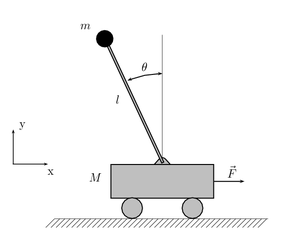
ในที่นี้เราจะหาแบบจำลองทางคณิตศาสตร์ของเพนดูลัมผกผันโดยใช้กลศาสตร์แบบลากรางจ์ (Lagrange's equations) และตั้งสมุมติฐานเพื่อความง่ายต่อความเข้าใจและยังคงไม่สูญเสียความเป็นรูปแบบทั่วไปว่าระบบเคลื่อนที่อยู่ในระนาบ 2 มิติ แกน $x-y$ ได้เท่านั้น โดยตัวแปรต่างๆเราจะอ้างอิงตัวแปรเดียวกับที่ปรากฏในภาพ กล่าวคือ $\theta (t)$ คือ มุมที่แท่งเพนดูลัมทำกับแนวตั้งฉากกับพื้นโลก และให้แท่งเพนดูลัมมีความยาว $l$ ให้แรงจากภายนอกเป็น $F$ กระทำในทิศ $x$ ดังภาพ และแรงโน้มถ่วงของโลกกระทำในแนวแกน $y$ และกำหนดให้ $x(t)$ เป็นระยะของรถในแกน $x$ ที่แปรผันตามเวลา และสมการลากรางจ์ (Lagrangian) ของระบบเป็นดังต่อไปนี้ $L=T-V$ โดย $T$ คือพลังงานจลน์ของระบบ และ $V$ คือพลังงานศักย์ของระบบ

รูปภาพแสดงรูปแบบของเพนดุลัมผกผันและตัวแปรที่ใช้ในการสร้างแบบจำลองทางคณิตศาสตร์

$L={\frac {1}{2}}Mv_{1}^{2}+{\frac {1}{2}}mv_{2}^{2}-mg\ell \cos \theta$
โดย $v_{1}$ เป็นความเร็วของของตัวรถ $v_{2}$ เป็นความเร็วของจุดศูนย์กลางมวล $m$ ของมวลบนแท่งเพนดูลัม.
ทั้งนี้ $v_{1}$ และ $v_{2}$ สามารถเขียนให้อยู่ในรูปของ $x$ และ $\theta$ ดังต่อไปนี้

$v_{1}^{2}={\dot {x}}^{2}$

$v_{2}^{2}=\left({\frac {d}{dt}}{\left(x-\ell \sin \theta \right)}\right)^{2}+\left({\frac {d}{dt}}{\left(\ell \cos \theta \right)}\right)^{2}$

ทำการลดรูป $v_{2}$ ได้ผลเป็น

$v_{2}^{2}={\dot {x}}^{2}-2\ell {\dot {x}}{\dot {\theta }}\cos \theta +\ell ^{2}{\dot {\theta }}^{2}$

แทนสมการข้างต้นลงในสมการลากรางจ์ ได้ว่า:

$L={\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}-m\ell {\dot {x}}{\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}-mg\ell \cos \theta$

และสมการการเคลื่อนที่:

${\frac {\mathrm {d} }{\mathrm {d} t}}{\partial {L} \over \partial {\dot {x}}}-{\partial {L} \over \partial x}=F$

${\frac {\mathrm {d} }{\mathrm {d} t}}{\partial {L} \over \partial {\dot {\theta }}}-{\partial {L} \over \partial \theta }=0$

แทนที่ $L$ ในสมการข้างต้นจะได้สมการที่อธิบายการเลือนที่ของเพนดูลัมแบบผกผันดังนี้

$\left(M+m\right){\ddot {x}}-m\ell {\ddot {\theta }}\cos \theta +m\ell {\dot {\theta }}^{2}\sin \theta =F$

$\ell {\ddot {\theta }}-g\sin \theta ={\ddot {x}}\cos \theta$

จะเห็นได้ว่าสมการที่ได้เป็นสมการไม่เชิงเส้นซึ่งยากที่จะนำไปออกแบบตัวควบคุม ในทางปฏิบัติผู้ออกแบบจะนิยมแปรงสมการไม่เชิงเส้นให้เป็นสมการเชิงเส้นก่อน โดยสมมุติว่าแท่งเพนดุลัมแกว่งอยู่ในช่วงมุมเล็ก ๆ ซึ่งประมาณเป็น $0$ ได้ ($\theta \approx 0$) ทั้งนี้เพื่อความง่ายต่อการออกแบบตัวควบคุม และง่ายต่อการอธิบายพฤติกรรมของระบบ

ดูเพิ่ม

• ทฤษฎีระบบควบคุม
• Segway
• เพนดูลัมผกผันแบบฟูรุตะ (Furuta pendulum)

แหล่งข้อมูลอื่น

• สื่อการสอนเกี่ยวกับทฤษฎีระบบควบคุม มีตัวอย่างเป็นเพนดูลัมแบบผกผัน ของ มหาวิทยาลัยคาร์เนกีเมลลอน เก็บถาวร 2007-05-22 ที่ เวย์แบ็กแมชชีน
• Katsuhiko Ogata, Modern control engineering (Edition 5), Prentice Hall, 2010, ISBN 0136156738,9780136156734
• Franklin; et al. (2005). Feedback control of dynamic systems, 5, Prentice Hall. ISBN 0-13-149930-0
• Norman S. Nise, Control Systems Engineering (Edition 6), John Wiley & Sons, 2010, ISBN 0470547561, 9780470547564
• เดวิด บรรเจิดพงศ์ชัย, ภาควิชาวิศวกรรมไฟฟ้า คณะวิศวกรรมศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย "ระบบควบคุมพลวัต การวิเคราะห์ การออกแบบ และการประยุกต์ (Dynamical Control Systems Analysis, Design and Applications)" สำนักพิมพ์แห่งจุฬาลงกรณ์มหาวิทยาลัย 2551 (ISBN 978-974-03-2205-4)
• วิบูลย์ แสงวีระพันธุ์ศิริ, ภาควิชาวิศวกรรมเครื่องกล คณะวิศวกรรมศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย "การควบคุมระบบพลศาสตร์ (Control of Dynamic Systems)" สำนักพิมพ์แห่งจุฬาลงกรณ์มหาวิทยาลัย 2548 (ISBN 974-13-3393-5)