ฟังก์ชันแกมมา
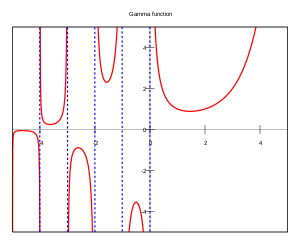
ฟังก์ชันแกมมา (อังกฤษ: Gamma function) เป็นฟังก์ชันทางคณิตศาสตร์ที่เป็นส่วนขยายของฟังก์ชันแฟกทอเรียลบนจำนวนเชิงซ้อน หรือสามารถกล่าวได้อีกอย่างหนึ่งว่า ฟังก์ชันแกมมาเป็นการเติมเต็มฟังก์ชันแฟกทอเรียลของค่า n ที่ไม่ใช่จำนวนเต็มบวกหรือศูนย์ สำหรับจำนวนเชิงซ้อน z ซึ่งส่วนจริงเป็นค่าบวก ได้นิยามไว้ว่า
นิยามดังกล่าวทำให้ผลลัพธ์สามารถขยายไปได้ถึงระนาบจำนวนเชิงซ้อน ยกเว้นเมื่อส่วนจริงเป็นจำนวนเต็มลบ สำหรับกรณีถ้า z มีค่าเป็นจำนวนเต็มบวก จะได้
ซึ่งแสดงให้เห็นว่ามีความเกี่ยวข้องกับฟังก์ชันแฟกทอเรียล
ฟังก์ชันแกมมาเป็นองค์ประกอบหนึ่งในฟังก์ชันที่เกี่ยวกับการกระจายและความน่าจะเป็นหลากหลายฟังก์ชัน นั่นหมายความว่าฟังก์ชันนี้นำไปใช้ได้ในเรื่องของความน่าจะเป็นและสถิติ
นิยาม[แก้]
นิยามหลัก[แก้]

สัญกรณ์ Γ (z) กำหนดขึ้นโดยอาเดรียง-มารี เลอช็องดร์ (Adrien-Marie Legendre) ซึ่งใช้อักษรกรีก แกมมา ตัวใหญ่ (Γ) แทนชื่อฟังก์ชัน โดยนิยามไว้ว่า ถ้าส่วนจริงของจำนวนเชิงซ้อน z เป็นค่าบวก (ℜ{z} > 0) ดังนั้นปริพันธ์นี้
จะลู่เข้าสัมบูรณ์ โดยการหาปริพันธ์ทีละส่วนจะสามารถแสดงได้ว่า
สมการเชิงฟังก์ชันนี้เป็นข้อสรุปทั่วไปสำหรับความสัมพันธ์ n! = n (n − 1) ! ของฟังก์ชันแฟกทอเรียล เราสามารถวิเคราะห์การประเมินค่าของ Γ (1) ได้ว่า
โดยการรวมความสัมพันธ์ข้างต้นสองประการ แสดงให้เห็นว่าฟังก์ชันแฟกทอเรียลเป็นกรณีพิเศษอันหนึ่งของฟังก์ชันแกมมา ดังนี้
สำหรับทุกค่า n ที่เป็นจำนวนธรรมชาติ ตัวอย่างเช่น Γ (5) = 4! เป็นต้น
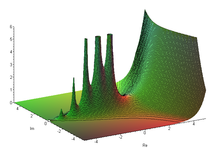
ความสัมพันธ์ดังกล่าวสามารถจัดเป็นฟังก์ชันมีโรมอร์ฟิก (meromorphic function) บนค่า x โดยมีโพล อยู่บน x = −n (เมื่อ n = 0, 1, 2, 3, ...) และมี ส่วนตกค้าง อยู่ที่ [1] ดังนั้นเราจะสามารถขยาย Γ (z) ไปเป็นฟังก์ชันมีโรมอร์ฟิกโดยนิยามให้มีค่าสำหรับทุกๆ ค่า z ที่เป็นจำนวนเชิงซ้อน ยกเว้นเมื่อ z = 0, −1, −2, −3, ... ตามการต่อเนื่องวิเคราะห์ (analytic continuation) ซึ่งส่วนขยายดังกล่าวมักเป็นการอ้างถึงฟังก์ชันแกมมาโดยปกติ
นิยามแบบอื่น[แก้]
เลออนฮาร์ด ออยเลอร์ และคาร์ล ไวแยร์สตราสส์ (Karl Weierstrass) ได้นิยามฟังก์ชันแกมมาโดยใช้ผลคูณอนันต์ ตามลำดับดังนี้
เมื่อ γ คือค่าคงที่ออยเลอร์-แมสเชโรนี ซึ่งสามารถใช้ได้กับทุกค่าของจำนวนเชิงซ้อน z ที่ไม่เท่ากับจำนวนเต็มลบหรือศูนย์
เราสามารถแสดงให้เห็นอย่างตรงไปตรงมาว่า นิยามของออยเลอร์สอดคล้องกับสมการเชิงฟังก์ชัน (1) ด้านบน เมื่อ z ไม่เท่ากับ 0, −1, −2, ...
คุณสมบัติ[แก้]
คุณสมบัติทั่วไป[แก้]
สมการเชิงฟังก์ชันอื่นสำหรับฟังก์ชันแกมมาที่สำคัญคือ สูตรการสะท้อนของออยเลอร์ (Euler's reflection formula)
และ สูตรการทำซ้ำ (duplication formula)
ซึ่งสูตรการทำซ้ำเป็นกรณีพิเศษกรณีหนึ่งของทฤษฎีบทการคูณ (multiplication theorem) ที่ว่า
อนึ่ง ค่าของฟังก์ชันแกมมา ซึ่งตัวแปรต้นไม่ได้เป็นจำนวนเต็ม ที่เป็นที่รู้จักมากที่สุดคือ
สามารถหาได้จากการแทนค่า z = 1/2 ลงในสูตรการสะท้อนด้านบน หรือจากฟังก์ชันบีตาโดยผ่านค่า (1/2, 1/2) ลงไป ซึ่งจะได้ผลลัพธ์ออกมาเท่ากับ π โดยทั่วไปแล้ว หากเราให้ n เป็นจำนวนคี่ เราจะได้คุณสมบัติอีกอย่างหนึ่งคือ
เมื่อ n!! หมายถึงดับเบิลแฟกทอเรียล
อนุพันธ์ของฟังก์ชันแกมมา สามารถอธิบายได้ในนิพจน์ของฟังก์ชันโพลีแกมมา ดังตัวอย่าง
ฟังก์ชันแกมมามีโพล (pole) อันดับ 1 อยู่ที่ z = −n สำหรับทุกค่าของ n ที่เป็นจำนวนธรรมชาติ และส่วนตกค้าง (residue) มีค่าเท่ากับ
ทฤษฎีบทบอร์-โมลเลอรัประบุว่า ในบรรดาฟังก์ชันทั้งหมดที่ขยายมาจากฟังก์ชันแฟกทอเรียลบนจำนวนจริงบวก มีเพียงฟังก์ชันแกมมาเท่านั้นที่เป็นฟังก์ชันคอนเวกซ์แบบลอการิทึม (logarithmically convex function) ซึ่งหมายความว่า ลอการิทึมธรรมชาติของฟังก์ชันแกมมาเป็นฟังก์ชันคอนเวกซ์ (convex function)
ฟังก์ชันพาย[แก้]
สัญกรณ์อีกรูปแบบหนึ่งซึ่งนำเสนอโดยคาร์ล ฟรีดริช เกาส์ คือ ฟังก์ชันพาย (Pi function, P ตัวใหญ่) ใช้อธิบายนิพจน์ของฟังก์ชันแกมมาว่า
ดังนั้น
โดยการใช้ฟังก์ชันพาย เราจึงสามารถเขียนสูตรการสะท้อนได้อีกรูปแบบหนึ่งดังนี้
เมื่อ "sinc" หมายถึงฟังก์ชันไซน์คาร์ดินัลแบบบรรทัดฐาน (normalized sinc function) ในขณะที่ทฤษฎีบทการคูณก็สามารถเขียนให้อยู่ในรูปของฟังก์ชันพายได้เช่นกัน
เรายังสามารถหาค่าของ
ซึ่งเป็นฟังก์ชันทั่ว (entire function) นิยามบนทุกค่าของจำนวนเชิงซ้อน และเนื่องจาก π (z) เป็นฟังก์ชันทั่ว นั่นคือฟังก์ชันดังกล่าวไม่มีโพล ดังนั้นผลลัพธ์ของ Γ (z) จึงไม่มีทางเป็นศูนย์
ความสัมพันธ์กับฟังก์ชันอื่น[แก้]
- ในตัวนิยามของฟังก์ชันแกมมาที่เป็นปริพันธ์ (สูตรแรกสุด) ขอบเขตของการหาปริพันธ์ได้ถูกกำหนดตายตัวไว้ ดังนั้นจึงมีการสร้างฟังก์ชันแกมมาไม่สมบูรณ์ (incomplete Gamma function) ในรูปแบบ Γ (a, x) ขึ้นมาเพื่อให้สามารถหาปริพันธ์ทั้งด้านซ้ายและด้านขวาของค่า x ใดๆ ก็ได้ที่อยู่ระหว่าง 0 ถึง ∞
- ฟังก์ชันแกมมามีความสัมพันธ์กับฟังก์ชันบีตาด้วยสูตรนี้
- อนุพันธ์ลอการิทึม (logarithmic derivative) ของฟังก์ชันแกมมาเรียกว่า ฟังก์ชันไดแกมมา (digamma function) และในอนุพันธ์ในอันดับสูงกว่าจะเรียกว่า ฟังก์ชันโพลีแกมมา (polygamma function)
- แอนะล็อกของฟังก์ชันแกมมาเหนือฟีลด์จำกัด (finite field) หรือริงจำกัด (finite ring) คือผลบวกเกาส์เซียน (Gaussian sum) ซึ่งเป็นผลบวกเลขชี้กำลัง (exponential sum) ชนิดหนึ่ง
- ฟังก์ชันแกมมาส่วนกลับ (reciprocal Gamma function) เป็นฟังก์ชันทั่วชนิดหนึ่งและเป็นหัวข้อที่ต้องศึกษาโดยเฉพาะ
- ฟังก์ชันแกมมายังมีความสัมพันธ์ที่สำคัญกับฟังก์ชันซีตาของรีมันน์ (Riemann zeta function) ซึ่งใช้สัญกรณ์ ζ (z) ดังนี้
และในอีกสูตรหนึ่งที่ดูเรียบง่ายคือ
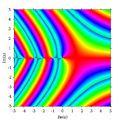
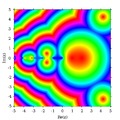
แผนภาพ[แก้]
-
ส่วนจริงของ Γ (z)
-
ส่วนจินตภาพของ Γ (z)
-
ค่าสัมบูรณ์ของ Γ (z)
-
ส่วนจริงของ log Γ (z)
-
ส่วนจินตภาพของ log Γ (z)
-
ค่าสัมบูรณ์ของ log Γ (z)
ค่าเฉพาะบางค่าที่ควรทราบ[แก้]
อ้างอิง[แก้]
- ↑ George Allen, and Unwin, Ltd., The Universal Encyclopedia of Mathematics. United States of America, New American Library, Simon and Schuster, Inc., 1964. (Forward by James R. Newman)
- Philip J. Davis, "Leonhard Euler's Integral: A Historical Profile of the Gamma Function," Am. Math. Monthly 66, 849-869 (1959)
- เอริก ดับเบิลยู. ไวส์สไตน์, "Gamma function" จากแมทเวิลด์.
- Pascal Sebah and Xavier Gourdon. Introduction to the Gamma Function. In PostScript and HTML formats.
- Bruno Haible & Thomas Papanikolaou. Fast multiprecision evaluation of series of rational numbers เก็บถาวร 2006-06-30 ที่ เวย์แบ็กแมชชีน. Technical Report No. TI-7/97, Darmstadt University of Technology, 1997
แหล่งข้อมูลอื่น[แก้]
แหล่งข้อมูลอื่น[แก้]
- Cephes - C and C++ language special functions math library
- Examples of problems involving the Gamma function can be found at Exampleproblems.com เก็บถาวร 2016-10-02 ที่ เวย์แบ็กแมชชีน.
- Gamma function calculator
- Wolfram gamma function evaluator (arbitrary precision)
- Gamma at the Wolfram Functions Site.
- Computing the Gamma function - various algorithms
หนังสือตำรา[แก้]
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 6)
- G. Arfken and H. Weber. Mathematical Methods for Physicists. Harcourt/Academic Press, 2000. (See Chapter 10.)
- Harry Hochstadt. The Functions of Mathematical Physics. New York: Dover, 1986 (See Chapter 3.)
- W.H. Press, B.P. Flannery, S.A. Teukolsky, and W.T. Vetterling. Numerical Recipes in C. Cambridge, UK: Cambridge University Press, 1988. (See Section 6.1.)