บรรทัด 29:
บรรทัด 29:
ในกรณีที่สองนั้น สมมุติฐานให้ <math>f</math> [[อนุกรมลู่ออก|ลู่ออก]]ไปอนันต์จะไม่ได้ถูกใช้ในบทพิสูจน์ (ดูหมายเหตุตรงท้ายหัวเรื่อง''บทพิสูจน์'') ดั้งนั้นโดยปกติเงื่อนไขของกฎจะกล่าวไว้ตามข้างบน เงื่อนไขที่เพียงพอที่สองที่จะทำให้กระบวนการของกฎนี้ถูกต้องสามารถกล่าวได้อย่างสั้น ๆ ว่า <math display="inline">\lim_{x \to c} |g(x)| = \infty </math>
ในกรณีที่สองนั้น สมมุติฐานให้ <math>f</math> [[อนุกรมลู่ออก|ลู่ออก]]ไปอนันต์จะไม่ได้ถูกใช้ในบทพิสูจน์ (ดูหมายเหตุตรงท้ายหัวเรื่อง''บทพิสูจน์'') ดั้งนั้นโดยปกติเงื่อนไขของกฎจะกล่าวไว้ตามข้างบน เงื่อนไขที่เพียงพอที่สองที่จะทำให้กระบวนการของกฎนี้ถูกต้องสามารถกล่าวได้อย่างสั้น ๆ ว่า <math display="inline">\lim_{x \to c} |g(x)| = \infty </math>
สมมุติฐานที่ว่า <math>g'(x) \ne 0</math> จะพบเห็นได้บ่อยตามงานเขียน แต่บางผู้เขียนละสมมุติฐานนี้โดยการเขียนสมมติฐานอื่น
สมมุติฐานที่ว่า <math>g'(x) \ne 0</math> จะพบเห็นได้บ่อยตามงานเขียน แต่บางผู้เขียนละสมมุติฐานนี้โดยการเขียนสมมติฐานอื่น วิธีหนึ่ง<ref>{{harv|Chatterjee|2005|loc=p. 291}}</ref>คือการนิยามลิมิตของฟังก์ชันนั้นโดยเพิ่มข้อกำหนดทีฟังก์ชันที่ใช้หาลิมิตนั้นต้องถูกนิยามทุกที่บนช่วงที่เกี่ยวข้อง <math>I</math> อาจยกเว้นที่ <math>c</math> อีกวิธี<ref>{{harv|Krantz|2004|loc=p.79}}</ref>คือให้ทั้ง <math>f</math> และ <math>g</math> จำเป็นที่จะต้องหาอนุพันธ์ได้ทุกที่บนช่วงที่มี <math>c</math> อยู่
== ตัวอย่าง ==
== ตัวอย่าง ==
บรรทัด 127:
บรรทัด 127:
== อ้างอิง ==
== อ้างอิง ==
<references />
<references />
=== แหล่งข้อมูล ===
* {{citation|last=Chatterjee|first=Dipak|title=Real Analysis|year=2005|publisher=PHI Learning Pvt. Ltd|isbn=81-203-2678-4}}
* {{citation|last=Krantz|first=Steven G.|title=A handbook of real variables. With applications to differential equations and Fourier analysis|pages=xiv+201|year=2004|place=Boston, MA|publisher=Birkhäuser Boston Inc.|doi=10.1007/978-0-8176-8128-9|isbn=0-8176-4329-X|mr=2015447}}
[[หมวดหมู่:แคลคูลัส]]
[[หมวดหมู่:แคลคูลัส]]
{{โครงคณิตศาสตร์}}
{{โครงคณิตศาสตร์}}
ตัวอย่างการประยุกต์ใช้ของกฎของโลปีตาล เมื่อ
f
(
x
)
=
sin
(
x
)
{\displaystyle {\color {orange}f(x)}=\color {orange}\sin(x)}
g
(
x
)
=
−
0.5
x
{\displaystyle {\color {red}g(x)}=\color {red}-0.5x}
h
(
x
)
=
f
(
x
)
/
g
(
x
)
{\displaystyle {\color {brown}h(x)}={\color {orange}f(x)}/{\color {red}g(x)}}
x = 0
R
{\displaystyle \mathbb {R} }
h
(
0
)
=
f
′
(
0
)
/
g
′
(
0
)
=
−
2
{\displaystyle {\color {brown}h(0)}={\color {teal}f'(0)}/{\color {blue}g'(0)}=-2}
ในแคลคูลัส กฎของโลปีตาล (อังกฤษ : L'Hôpital's rule) หรือ กฎของแบร์นูลลี (อังกฤษ : ฺBernoulli's rule) เป็นทฤษฎีบทคณิตศาสตร์ที่ว่าด้วยการหาค่าลิมิต ที่อยู่ในรูปแบบยังไม่กำหนด (อังกฤษ : indeterminate forms) ด้วยการใช้อนุพันธ์ กฎนี้มักนำมาใช้ในการเปลี่ยนรูปแบบยังไม่กำหนด เป็นรูปแบบกำหนด เพื่อให้ง่ายต่อการคำนวณลิมิตโดยการแทนค่าเข้าไปตรง ๆ กฎนี้ถูกตั้งชื่อตามนักคณิตศาสตร์ ชาวฝรั่งเศส กีโยม เดอ โลปีตาล ถึงแม้กฎนี้มักถูกพิจารณาว่าถูกเขียนโดยเดอ โลปีตาล แต่ทฤษฎีบทนี้แบร์นูลลีเป็นคนเสนอให้กับเขา
ประวัติ กีโยม เดอ โลปีตาล เผยแพร่กฎนี้ในปีพ.ศ.2239 (ค.ศ.1696) ในหนังสือชื่อ Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes แคลคูลัสเชิงอนุพันธ์ [1] โยฮันน์ แบร์นูลลี [2]
รูปทั่วไป รูปทั่วไปของกฎของโลปีตาลครอบคลุมหลากหลายกรณี ให้
c
{\displaystyle c}
L
{\displaystyle L}
จำนวนจริงส่วนขยาย (ต.ย. จำนวนจริง อนันต์บวก อนันต์ลบ) ให้
I
{\displaystyle I}
ช่วงเปิด ที่มี
c
{\displaystyle c}
c
{\displaystyle c}
ลิมิตข้างเดียว หรือลิมิตที่อนันต์ ถ้า
c
{\displaystyle c}
f
{\displaystyle f}
g
{\displaystyle g}
หาอนุพันธ์ได้ บน
I
{\displaystyle I}
c
{\displaystyle c}
g
′
(
x
)
≠
0
{\displaystyle g'(x)\neq 0}
I
{\displaystyle I}
c
{\displaystyle c}
lim
x
→
c
f
′
(
x
)
g
′
(
x
)
=
L
{\textstyle \lim \limits _{x\to c}{\frac {f'(x)}{g'(x)}}=L}
x
{\displaystyle x}
c
{\displaystyle c}
ถ้า
lim
x
→
c
f
(
x
)
=
lim
x
→
c
g
(
x
)
=
0
{\displaystyle \lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0}
หรือ
lim
x
→
c
|
f
(
x
)
|
=
lim
x
→
c
|
g
(
x
)
|
=
∞
{\displaystyle \lim _{x\to c}|f(x)|=\lim _{x\to c}|g(x)|=\infty }
อย่างใดอย่างหนึ่งแล้ว
lim
x
→
c
f
(
x
)
g
(
x
)
=
L
{\displaystyle \lim _{x\to c}{f(x) \over g(x)}=L}
ถึงแม้ว่าเราจะเขียนในรูป
x
→
c
{\displaystyle x\to c}
x
→
c
+
{\displaystyle x\to c^{+}}
x
→
c
−
{\displaystyle x\to c^{-}}
c
{\displaystyle c}
I
{\displaystyle I}
ในกรณีที่สองนั้น สมมุติฐานให้
f
{\displaystyle f}
ลู่ออก ไปอนันต์จะไม่ได้ถูกใช้ในบทพิสูจน์ (ดูหมายเหตุตรงท้ายหัวเรื่องบทพิสูจน์ ) ดั้งนั้นโดยปกติเงื่อนไขของกฎจะกล่าวไว้ตามข้างบน เงื่อนไขที่เพียงพอที่สองที่จะทำให้กระบวนการของกฎนี้ถูกต้องสามารถกล่าวได้อย่างสั้น ๆ ว่า
lim
x
→
c
|
g
(
x
)
|
=
∞
{\textstyle \lim _{x\to c}|g(x)|=\infty }
สมมุติฐานที่ว่า
g
′
(
x
)
≠
0
{\displaystyle g'(x)\neq 0}
[3]
I
{\displaystyle I}
c
{\displaystyle c}
[4]
f
{\displaystyle f}
g
{\displaystyle g}
c
{\displaystyle c}
ตัวอย่าง ตัวอย่างพื้นฐานที่มีฟังก์ชันเลขชี้กำลัง ในรูปแบบยังไม่กำหนด
0
0
{\displaystyle {\frac {0}{0}}}
x
=
0
{\displaystyle x=0}
lim
x
→
0
e
x
−
1
x
2
+
x
=
lim
x
→
0
d
d
x
(
e
x
−
1
)
d
d
x
(
x
2
+
x
)
=
lim
x
→
0
e
x
2
x
+
1
=
1
{\displaystyle {\begin{aligned}\lim _{x\to 0}{\frac {e^{x}-1}{x^{2}+x}}&=\lim _{x\to 0}{\frac {{\frac {d}{dx}}(e^{x}-1)}{{\frac {d}{dx}}(x^{2}+x)}}\\[4pt]&=\lim _{x\to 0}{\frac {e^{x}}{2x+1}}\\[4pt]&=1\end{aligned}}}
ตัวอย่างที่ซับซ้อนขึ้นที่เป็น
0
0
{\displaystyle {\frac {0}{0}}}
lim
x
→
0
2
sin
(
x
)
−
sin
(
2
x
)
x
−
sin
(
x
)
=
lim
x
→
0
2
cos
(
x
)
−
2
cos
(
2
x
)
1
−
cos
(
x
)
=
lim
x
→
0
−
2
sin
(
x
)
+
4
sin
(
2
x
)
sin
(
x
)
=
lim
x
→
0
−
2
cos
(
x
)
+
8
cos
(
2
x
)
cos
(
x
)
=
−
2
+
8
1
=
6
{\displaystyle {\begin{aligned}\lim _{x\to 0}{\frac {2\sin(x)-\sin(2x)}{x-\sin(x)}}&=\lim _{x\to 0}{\frac {2\cos(x)-2\cos(2x)}{1-\cos(x)}}\\[4pt]&=\lim _{x\to 0}{\frac {-2\sin(x)+4\sin(2x)}{\sin(x)}}\\[4pt]&=\lim _{x\to 0}{\frac {-2\cos(x)+8\cos(2x)}{\cos(x)}}\\[4pt]&={\frac {-2+8}{1}}\\[4pt]&=6\end{aligned}}}
ตัวอย่างที่เป็น
∞
∞
{\displaystyle {\frac {\infty }{\infty }}}
lim
x
→
∞
x
n
e
x
=
lim
x
→
∞
n
x
n
−
1
e
x
=
n
⋅
lim
x
→
∞
x
n
−
1
e
x
{\displaystyle \lim _{x\to \infty }{\frac {x^{n}}{e^{x}}}=\lim _{x\to \infty }{\frac {nx^{n-1}}{e^{x}}}=n\cdot \lim _{x\to \infty }{\frac {x^{n-1}}{e^{x}}}}
n
{\displaystyle n}
n
{\displaystyle n}
ตัวอย่างที่เป็นรูปแบบยังไม่กำหนด
0
⋅
∞
{\displaystyle 0\cdot \infty }
∞
∞
{\displaystyle {\frac {\infty }{\infty }}}
lim
x
→
0
+
x
ln
x
=
lim
x
→
0
+
ln
x
1
x
=
lim
x
→
0
+
1
x
−
1
x
2
=
lim
x
→
0
+
−
x
=
0.
{\displaystyle \lim _{x\to 0^{+}}x\ln x=\lim _{x\to 0^{+}}{\frac {\ln x}{\frac {1}{x}}}=\lim _{x\to 0^{+}}{\frac {\frac {1}{x}}{-{\frac {1}{x^{2}}}}}=\lim _{x\to 0^{+}}-x=0.}
รูปแบบยังไม่กำหนดอื่น ๆ รูปแบบยังไม่กำหนดอื่น ๆ เช่น
1
∞
{\displaystyle 1^{\infty }}
0
0
{\displaystyle 0^{0}}
∞
0
{\displaystyle \infty ^{0}}
0
⋅
∞
{\displaystyle 0\cdot \infty }
∞
−
∞
{\displaystyle \infty -\infty }
∞
−
∞
{\displaystyle \infty -\infty }
lim
x
→
1
(
x
x
−
1
−
1
ln
x
)
=
lim
x
→
1
x
⋅
ln
x
−
x
+
1
(
x
−
1
)
⋅
ln
x
(
1
)
=
lim
x
→
1
ln
x
x
−
1
x
+
ln
x
(
2
)
=
lim
x
→
1
x
⋅
ln
x
x
−
1
+
x
⋅
ln
x
(
3
)
=
lim
x
→
1
1
+
ln
x
1
+
1
+
ln
x
(
4
)
=
lim
x
→
1
1
+
ln
x
2
+
ln
x
=
1
2
{\displaystyle {\begin{aligned}\lim _{x\to 1}\left({\frac {x}{x-1}}-{\frac {1}{\ln x}}\right)&=\lim _{x\to 1}{\frac {x\cdot \ln x-x+1}{(x-1)\cdot \ln x}}&\quad (1)\\[6pt]&=\lim _{x\to 1}{\frac {\ln x}{{\frac {x-1}{x}}+\ln x}}&\quad (2)\\[6pt]&=\lim _{x\to 1}{\frac {x\cdot \ln x}{x-1+x\cdot \ln x}}&\quad (3)\\[6pt]&=\lim _{x\to 1}{\frac {1+\ln x}{1+1+\ln x}}&\quad (4)\\[6pt]&=\lim _{x\to 1}{\frac {1+\ln x}{2+\ln x}}\\[6pt]&={\frac {1}{2}}\\\end{aligned}}}
กฎของโลปีตาลถูกใช้ในขั้นตอนจาก (1) ไป (2) และอีกครั้งในขั้นตอน (3) ไป (4)
กฎของโลปีตาลใช้ได้กับรูปแบบยังไม่กำหนดที่มีเลขยกกำลัง โดยใช้ลอการิทึม ช่วย"ตบเลขยกกำลังลงมา" ตัวอย่างเช่น
lim
x
→
0
+
x
x
=
lim
x
→
0
+
e
ln
(
x
x
)
=
lim
x
→
0
+
e
x
⋅
ln
x
=
e
lim
x
→
0
+
(
x
⋅
ln
x
)
{\displaystyle \lim _{x\to 0^{+}}x^{x}=\lim _{x\to 0^{+}}e^{\ln(x^{x})}=\lim _{x\to 0^{+}}e^{x\cdot \ln x}=e^{\lim \limits _{x\to 0^{+}}(x\cdot \ln x)}}
ย้ายลิมิตเข้าไปในฟังก์ชันเลขชี้กำลัง ได้เพราะฟังก์ชันเลขชี้กำลังเป็นฟังก์ชันต่อเนื่อง และการที่เลขชี้กำลัง
x
{\displaystyle x}
lim
x
→
0
+
x
⋅
ln
x
{\displaystyle \lim _{x\to 0^{+}}x\cdot \ln x}
0
⋅
∞
{\displaystyle 0\cdot \infty }
lim
x
→
0
+
x
⋅
ln
x
=
0
{\displaystyle \lim _{x\to 0^{+}}x\cdot \ln x=0}
lim
x
→
0
+
x
x
=
e
0
=
1
{\displaystyle \lim _{x\to 0^{+}}x^{x}=e^{0}=1}
ตารางต่อไปนี้คือรายการรูปแบบยังไม่กำหนดที่พบบ่อย กับการแปลงโดยใช้กฎโลปีตาล
รูปแบบยังไม่กำหนด
เงื่อนไข
การแปลงเป็น
0
/
0
{\displaystyle 0/0}
0 / 0
lim
x
→
c
f
(
x
)
=
0
,
lim
x
→
c
g
(
x
)
=
0
{\displaystyle \lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=0\!}
—
∞
{\displaystyle \infty }
/
∞
{\displaystyle \infty }
lim
x
→
c
f
(
x
)
=
∞
,
lim
x
→
c
g
(
x
)
=
∞
{\displaystyle \lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!}
lim
x
→
c
f
(
x
)
g
(
x
)
=
lim
x
→
c
1
/
g
(
x
)
1
/
f
(
x
)
{\displaystyle \lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {1/g(x)}{1/f(x)}}\!}
0
⋅
∞
{\displaystyle 0\cdot \infty }
lim
x
→
c
f
(
x
)
=
0
,
lim
x
→
c
g
(
x
)
=
∞
{\displaystyle \lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=\infty \!}
lim
x
→
c
f
(
x
)
g
(
x
)
=
lim
x
→
c
f
(
x
)
1
/
g
(
x
)
{\displaystyle \lim _{x\to c}f(x)g(x)=\lim _{x\to c}{\frac {f(x)}{1/g(x)}}\!}
∞
−
∞
{\displaystyle \infty -\infty }
lim
x
→
c
f
(
x
)
=
∞
,
lim
x
→
c
g
(
x
)
=
∞
{\displaystyle \lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!}
lim
x
→
c
(
f
(
x
)
−
g
(
x
)
)
=
lim
x
→
c
1
/
g
(
x
)
−
1
/
f
(
x
)
1
/
(
f
(
x
)
g
(
x
)
)
{\displaystyle \lim _{x\to c}(f(x)-g(x))=\lim _{x\to c}{\frac {1/g(x)-1/f(x)}{1/(f(x)g(x))}}\!}
0
0
{\displaystyle 0^{0}}
lim
x
→
c
f
(
x
)
=
0
+
,
lim
x
→
c
g
(
x
)
=
0
{\displaystyle \lim _{x\to c}f(x)=0^{+},\lim _{x\to c}g(x)=0\!}
lim
x
→
c
f
(
x
)
g
(
x
)
=
exp
lim
x
→
c
g
(
x
)
1
/
ln
f
(
x
)
{\displaystyle \lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!}
1
∞
{\displaystyle 1^{\infty }}
lim
x
→
c
f
(
x
)
=
1
,
lim
x
→
c
g
(
x
)
=
∞
{\displaystyle \lim _{x\to c}f(x)=1,\ \lim _{x\to c}g(x)=\infty \!}
lim
x
→
c
f
(
x
)
g
(
x
)
=
exp
lim
x
→
c
ln
f
(
x
)
1
/
g
(
x
)
{\displaystyle \lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!}
∞
0
{\displaystyle \infty ^{0}}
lim
x
→
c
f
(
x
)
=
∞
,
lim
x
→
c
g
(
x
)
=
0
{\displaystyle \lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=0\!}
lim
x
→
c
f
(
x
)
g
(
x
)
=
exp
lim
x
→
c
g
(
x
)
1
/
ln
f
(
x
)
{\displaystyle \lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!}
อ้างอิง
↑ O'Connor, John J.; Robertson, Edmund F. "De L'Hopital biography" . The MacTutor History of Mathematics archive . Scotland: School of Mathematics and Statistics, University of St Andrews. สืบค้นเมื่อ 21 December 2008 . {{cite web }}: CS1 maint: url-status (ลิงก์ )↑ Boyer, Carl B.; Merzbach, Uta C. (2011-01-25). A History of Mathematics ISBN 978-0-470-63056-3 ↑ (Chatterjee 2005 , p. 291)
↑ (Krantz 2004 , p.79)
แหล่งข้อมูล Chatterjee, Dipak (2005), Real Analysis , PHI Learning Pvt. Ltd, ISBN 81-203-2678-4 Krantz, Steven G. (2004), A handbook of real variables. With applications to differential equations and Fourier analysis , Boston, MA: Birkhäuser Boston Inc., pp. xiv+201, doi :10.1007/978-0-8176-8128-9 , ISBN 0-8176-4329-X MR 2015447 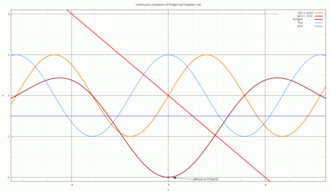





























![{\displaystyle {\begin{aligned}\lim _{x\to 0}{\frac {e^{x}-1}{x^{2}+x}}&=\lim _{x\to 0}{\frac {{\frac {d}{dx}}(e^{x}-1)}{{\frac {d}{dx}}(x^{2}+x)}}\\[4pt]&=\lim _{x\to 0}{\frac {e^{x}}{2x+1}}\\[4pt]&=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61dc9bd7af6ec9ab9e48ff29b32da5114f95a666)
![{\displaystyle {\begin{aligned}\lim _{x\to 0}{\frac {2\sin(x)-\sin(2x)}{x-\sin(x)}}&=\lim _{x\to 0}{\frac {2\cos(x)-2\cos(2x)}{1-\cos(x)}}\\[4pt]&=\lim _{x\to 0}{\frac {-2\sin(x)+4\sin(2x)}{\sin(x)}}\\[4pt]&=\lim _{x\to 0}{\frac {-2\cos(x)+8\cos(2x)}{\cos(x)}}\\[4pt]&={\frac {-2+8}{1}}\\[4pt]&=6\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1a3d962ee862222679e01afff611a616cd38e64)









![{\displaystyle {\begin{aligned}\lim _{x\to 1}\left({\frac {x}{x-1}}-{\frac {1}{\ln x}}\right)&=\lim _{x\to 1}{\frac {x\cdot \ln x-x+1}{(x-1)\cdot \ln x}}&\quad (1)\\[6pt]&=\lim _{x\to 1}{\frac {\ln x}{{\frac {x-1}{x}}+\ln x}}&\quad (2)\\[6pt]&=\lim _{x\to 1}{\frac {x\cdot \ln x}{x-1+x\cdot \ln x}}&\quad (3)\\[6pt]&=\lim _{x\to 1}{\frac {1+\ln x}{1+1+\ln x}}&\quad (4)\\[6pt]&=\lim _{x\to 1}{\frac {1+\ln x}{2+\ln x}}\\[6pt]&={\frac {1}{2}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d20b9715e349d99ea36894fe15b36cb47a400eda)
















