ฉบับร่าง:พีชคณิตเชิงเรขาคณิต
ระวังสับสนกับเรขาคณิตเชิงพีชคณิต
ในทางคณิตศาสตร์ พีชคณิตเชิงเรขาคณิต (อังกฤษ: geometric algebra: GA) (และรู้จักในชื่อพีชคณิตแบบคลิฟฟอร์ด) เป็นส่วนขยายของพีชคณิตมูลฐานเพื่อใช้กับวัตถุทางเรขาคณิต เช่น เวกเตอร์ พีชคณิตเชิงเรขาคณิตสร้างขึ้นจากการตำเนินการมูลฐานสองตัวคือการบวกและผลคูณเชิงเรขาคณิต การคูณเวกเตอร์ให้ผลลัพธ์ในมิติที่สูงขึ้นเรียกมัลติเวกเตอร์ เมื่อเทียบกับรูปนัยนิยมอื่นที่กระทำกับวัตถุทางเรขาคณิต น่าสังเกตว่าพีชคณิตเชิงเรขาคณิตมีการหารเวกเตอร์ (แต่โดยทั้วไปไม่ทุกสมาชิกที่ทำได้) และการบวกของวัตถุต่างมิติ
แฮร์มัน กรัสมันได้อธีบายผลคูณเชิงเรขาคณิตนี้ไว้สั้น ๆ โดยมากเขาสนใจพัฒนาพีชคณิตภายนอกซึ่งคล้าย ๆ กัน ในปีค.ศ.1878 วิลเลียม คิงดอน คลิฟฟอร์ดได้ขยายผลงานของกรัสมันได้สร้างสิ่งที่ตอนนี้โดยทั่วไปเรียกกันว่าพีชคณิตแบบคลิฟฟอร์ดเพื่อเป็นเกียรติแก่เขา (แต่คลิฟฟอร์ดเองเลือกที่จะเรียกว่าพีชคณิตเชิงเรขาคณิต) คลิฟฟอร์ดได้นิยามพีชคณิตแบบคลิฟฟอร์ดกับผลของมันไว้ว่าเป็นการรวมกันของพีชคณิตแบบกรัสมันและพีชคณิตควอเทอร์เนียน การเพิ่มคู่ของผลคูณภายนอกกรัสมันยอมให้การใช้พีชคณิตแบบกรัสมัน-เคย์ลี และแบบคงรูปของอันหลังรวมกับพีชคณิตแบบคลิฟฟอร์ดแบบคงรูปผลให้เกิดพีชคณิตเชิงเรขาคณิตแบบคงรูป (อังกฤษ: conformal geometric algebra: CGA) ให้โครงร่างสำหรับเรขาคณิตแบบฉบับ ในทางปฏิบัติ การตำเนินการเหล่านี้และอนุพันธ์ยอมให้เกิดการสมนัยกันของสมาชิก ปริภูมิย่อยและการตำเนินการของพีชคณิตที่มีความหมายทางเรขาคณิต เป็นเวลาหลายทศวรรษที่พีชคณิตเชิงเรขาคณิตค่อนข้างถูกละเลย ถูกบดบังไปมากโดยแคลคูลัสเวกเตอร์แล้วพัฒาขึ้นใหม่เพื่ออธิบายแม่เหล็กไฟฟ้า คำว่า"พีชคณิตเชิงเรขาคณิต"เป็นที่นิยมอีกครั้งในช่วงทศวรรษ1960 โดยเฮสเทเนส ผู้บอกความสำคัญต่อฟิสิกส์สัมพัทธภาพ
สเกลาร์และเวกเตอร์มีความหมายเหมือนปกติ และประกอบเป็นปริภูมิย่อยที่เด่นชัดในพีชคณิตเชิงเรขาคณิต ไบเวกเตอร์เป็นตัวแทนที่ธรรมชาติกว่าของปริมาณเวกเตอร์เทียมของแคลคูลัสเวกเตอร์ โดยปกติจะนิยามโดยใช้ผลคูณเชิงเวกเตอร์ เช่น พื้นที่กำหนดทิศ มุมหมุนกำหนดทิศ ทอร์ค โมเมนตัมเชิงมุม และสนามแม่เหล็ก ไทรเวกเตอร์สามารถแทนปริมาตรกำหนดทิศ และอื่น ๆ สมาชิกตัวหนึ่งเรียกว่าเบลดอาจใช้แทนปริภูมิย่อยของ และภาพฉายเชิงตั้งฉากบนปริภูมิย่อยนั้น การหมุนและการสะท้อนจะแสดงเป็นสมาชิก ต่างจากพีชคณิตเวกเตอร์ พีชคณิตเชิงเรขาคณิตโดยธรรมชาติจะรองรับมิติจำนวนเท่าไหร่ก็ได้ และรูปกำลังสองใด ๆ เช่นในสัมพัทธภาพ
ตัวอย่างการใช้งานพีชคณิตเชิงเรขาคณิตในฟิสิกส์ได้แก่ พีชคณิตกาลากาศ(และที่ไม่พบบ่อยพีชคณิตของปริภูมิกายภาพ) และพีชคณิตเชิงเรขาคณิตแบบคงรูป แคลคูลัสเชิงเรขาคณิต ส่วนขยายของพีชคณิตเชิงเรขาคณิตที่รวมอนุพันธ์และปริพันธ์ สามารถใช้กำหนดทฤษฎีอื่น ๆ เช่นการวิเคราะห์เชิงซ้อน และเรขาคณิตเชิงอนุพันธ์ ต.ย. โดยใช้พีชคณิตแบบคลิฟฟอร์ดแทนรูปแบบเชิงอนุพันธ์ พีชคณิตเชิงเรขาคณิตได้รับการสนับสนุนจากโดยเฉพาะเดวิด เฮสเทเนสและคริส ดอรัน ให้เป็นกรอบทางคณิตศาสตร์ที่ต้องการสำหรับฟิสิกส์ ผู้เสนออ้างว่าให้คำอธิบายที่กระทัดรัดและเข้าใจง่ายในหลายสาขารวมทั้งกลศาสตร์แบบฉบับและควอนตัม ทฤษฎีแม่เหล็กไฟฟ้า และสัมพัทธภาพ พีชคณิตเชิงเรขาคณิตยังสามารถใช้เป้นเครื่องมือในการคำนวนในคอมพิวเตอร์กราฟิกส์ และวิทยาการหุ่นยนต์
นิยามและสัญกรณ์
[แก้]มีหลากหลายวิธีที่นิยามระบบพีชคณิตเชิงเรขาคณิต วิธีดั้งเดิมของเฮสเทเนสเป็นเชิงสัจพจน์ "เต็มไปด้วยความสำคัญทางเรขาคณิต" และสมมูลกับพีชคณิตแบบคลิฟฟอร์ดสากล
ให้ปริภูมิเวกเตอร์มิติจำกัด บนฟีลด์ ด้วยรูปแบบเชิงเส้นคู่สมมาตร (การคูณภายใน ต.ย. ยูคลิเดียนหรือลอเรนต์เซียนเมตริก) พีชคณิตเชิงเรขาคณิตของปริภูมิกำลังสอง นั้นเป็นพีชคณิตแบบคลิฟฟอร์ด สมาชิกในนั้นเรียกว่ามัลติเวกเตอร์ พีชคณิตแบบคลิฟฟอร์ดโดยทั่วไปแล้วจะกำหนดนิยามเป็นพีชคณิตผลหารของพีชคณิตเทนเซอร์ แต่การกำหนดนิยามแบบนี้นามธรรม ดั้งนั้นนิยามดังต่อไปนี้จะเสนอโดยไม่ต้องใช้พีชคณิตนามธรรม
นิยาม — พีชคณิตการเปลี่ยนหมู่เอกลักษณ์ ที่มีรูปแบบเชิงเส้นคู่ปรกคิ เป็นพีชคณิตแบบคลิฟฟอร์ดของปริภูมิกำลังสอง ถ้า
- มี และ เป็นปริภูมิย่อยแยกกัน
- สำหรับ
- ก่อกำเนิด เป็นพีชคณิต
- ไม่ได้ถูกก่อกำเนิดโดยปริภูมิย่อยแท้ของ
เพื่อปกปิดรูปแบบเชิงเส้นคู่สมมาตรลดรูป เงื่อนไขสุดท้ายต้องได้รับการแก้ไข สามารถแสดงได้ว่าเงื่อนไขหล่าวนี้บอกได้ว่าเป็นผลคูณเชิงเรขาคณิตเพียงอย่างเดียว
สำหรับที่เหลือของบทความนี้ จะพิจรณาแต่กรณีจริงที่ สัญกรณ์ ( ตามลำดับ) จะใช้แสดงระบบพีชคณิตเชิงเรขาคณิตที่มีรูปแบบเชิงเส้นคู่ มีซิกเนเจอร์เป็น ( ตามลำดับ)
ผลคูณในพีชคณิตนี้เรียกว่าผลคูณเชิงเรขาตณิต และผลคูณในพีชคณิตภายนอกที่มีอยู่เรียกว่าผลคูณภายนอก (บ่อยครั้งเรียกว่าผลคูณลิ่ม) โดยมาตรฐานจะแสดงการคูณเหล่านี้โดยการเขียนติดกัน (โดยไม่เขียนสัญกรณ์การคูณ) และสัญกรณ์ ตามลำดับ
นิยามที่ได้กล่าวไปนั้นยังค่อนข้างเป็นนามธรรม ดังนั้นจะสรุปสมบัติของผลคูณเชิงเรขาคณิตที่นี่ สำหรับมัลติเวกเตอร์ :
- (สมบัติการปิด)
- เมื่อ เป็นสมาชิกเอกลักษณ์ (การมีอยู่ของสมาชิกเอกลักษณ์)
- (สมบัติการเปลี่ยนหมู่)
- และ (สมบัติการแจกแจง)
- สำหรับ
ผลคูณภายนอกมีสมบัติเหมือนกัน ยกเว้นสมบัติสุดท้ายได้รับการแทนที่โดย สำหรับ
สังเกตว่าในสมบัติสุดท้ายข้างบน จำนวนจริง ไม่จำเป็นต้องไม่เป็นลบ ถ้า ไม่เป็นบวกแน่นอน สมบัติที่สำคัญหนึ่งของผลคูณเชิงเรขาคณิตคือการมีอยู่ของสมาชิกที่มีตัวผกผันการคูณ สำหรับเวกเตอร์ ถ้า แล้ว มีเท่ากับ สมาชิกที่ไม่ใช่ศูนย์ของพีชคณิตนี้ไม่จำเป็นว่าจะมีตัวผกผันการคูณเสมอ ตัวอย่างเช่น ถ้า เป็นเวกเตอร์ใน เมื่อ แล้วสมาชิก จะเป็นทั้งสมาชิกนิจพลไม่ชัดและตัวหารของศูนย์ ดังนั้นจึงไม่มีตัวผกผัน
โดยปกติจะระบุ และ กับเรนจ์ภายใต้การซ้อนธรรมชาติ และ ในบทความนี้ การระบุนี้จะได้รับการสมมติ โดยตลอด คำว่าสเกลาร์และเวกเตอร์จะอ้างถึงสมาชิกของ และ ตามลำดับ (และเรนจ์ภายใต้การซ้อนนี้)
ผลคูณเชิงเรขาคณิต
[แก้]
สำหรับเวกเตอร์ และ เราสามารถเขียนผลคูณเชิงเรขาคณิตของสองเวกเดอร์ใด ๆ และ เป็นผลบวกของผลคูณสมมาตรและผลคูณอสมมาตร
จึงกำหนดนิยามของการคูณภายในเป็น
ทำให้ผลคูณสมมาตรสามาตรเขียนได้เป็น
ในทางกลับกัน ได้รับการกำหนดอย่างสมบูรณ์โดยพีชคณิตนี้ ผลคูณอสมมาตรคือผลคูนภายนอกของสองเวกเตอร์ ผลคูณของพีชคณิตภายนอกที่อยู่ภายใน
แล้วโดยการบวกตรง ๆ
คือรูปไม่ทั่วไปหรือรูปเวกเตอร์ของผลคูณเชิงเรขาคณิต
ผลคูณภายในและภายนอกมีความสัมพันธ์กับแนวคิดในพีชคณิตเวกเตอร์ ในทางเรขขาคณิต และ จะขนานก็ต่อเมื่อผลคูณเชิงเรขาคณิตเท่ากับผลคูณภายใน ในทางกลับกัน และ จะตั้งฉากก็ต่อเมื่อผลคูณเชิงเรขาคณิตเท่ากับผลคูณภายนอก ในระบบพีชคณิตเชิงเรขาคณิตซึ่งกำลังสองของเวกเตอร์ที่ไม่ใช่ศูนย์เป็นบวก ผลคูณภายในของเวกเตอร์ทั้งสองสามารถระบุได้ว่าคือผลคูณจุดในพีชคณิตเวกเตอร์ ผลคูณภายนอกสามารถระบุได้ว่าคือพื้นที่มีเครื่องหมายที่โดนล้อมโดยสี่เหลี่ยมด้านขนานโดยมีด้านเป็นเวกเตอร์ ผลคูณไขว้ของสองเวกเตอร์ใน มิติที่มีรูปแบบกำลังสองเป็นบวกแน่นอนดกี่ยวข้องอย่างใกล้ชิดกับผลคูณภายนอก
ระบบพีชคณิตเชิงเรขาคณิตที่สนใจส่วนใหญ่มีรูปแบบกำลังสองไม่ลดรูป ถ้ารูปแบบกำลังสองลดรูปโดยสมบูรณ์แล้ว ผลคูณภายในระหว่างสองเวกเตอร์ใด ๆ จะมีค่าเป็นศูนย์ และระบบพีชคณิตเชิงเรขาคณิตนั้นจะเป็นเพียงแค่ระบบระบบพีชคณิตภายนอก บทความนี้จะพูดถีงระบบพีชคณิตเชิงเรขาคณิตที่ไม่ลดรูป เว้นแต่จะระบุไว้
ผลคูณภายนอกโดยธรรมชาติจะขยายเป็นตัวดำเนินการทวิภาคเชิงเส้นคู่เปลี่ยนหมู่ได้ของสองสมาชิกในระบบพีชคณิต สอดคล้องกับเอกลักษณ์
เมื่อผลบวกรวมทุกการสับเปลี่ยนของเลขดัชนี ที่มี เป็นเครื่องหมายของการสับเปลี่ยน และ เป็นเวกเตอร์ (ไม่ใช้สมาชิกทั่วไปของระบบพีชคณิต) เนื่องจากทุกสามชิกของระบบพีชคณิตสามารถเขียนในรูปของผลบวกของผลคูณในรูปนี้ สามารถนิยามผลคูณภายนอกสำหรับทุกคู่ของสมาชิกระบบพีชคณิต สิ่งที่ตามมาคือผลคูณภายนอกก่อระบบพีชคณิตสลับ
เบลด เกรด และฐานหลัก
[แก้]มัลติเวกเตอร์ที่เป็นผลคูณภายนอกของ เวกเตอร์ที่อิสระเชิงเส้นเรียกว่าเบลด และมีเกรด มัลติเวกเตอร์ที่เป็นผลบวกของเบลดเกรด เรียกว่ามัลติเวกเตอร์(เอกพันธุ์)เกรด จากสัจพจน์สมบัติการปิด ทุกมัลติเวกเตอร์ที่เป็นผลบวกของเบลด
การจำลองทางเรขาคณิต
[แก้]ความหมายทางเรขาคณิตในแบบจำลองปริภูมิเวกเตอร์
[แก้]การฉาย และรีเจกชัน
[แก้]สำหรับเวกเตอร์ ใด ๆ และเวกเตอร์ ใด ๆ ที่หาตัวผกผันได้
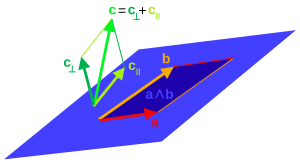
เมื่อภาพฉายของ บน (หรือส่วนขนาน) คือ
และฺรีเจกชันของ จาก (หรือส่วนที่ตั้งฉาก) คือ
ใช้แนวคิดว่า -เบลด เป็นตัวแทนปริภูมิย่อยของ และทุกมัลติเวกเตอร์มารถเขียนในรูปของพจ์ของเวกเตอร์ สามารวางนัยการฉายของมัลติเวกเตอร์ทั่วไปบน -เบลด ที่หาตัวผกผันได้ ให้อยู่ในรูปทั่วไปได้เป็น
และรีเจกชันสามารถนิยามได้เป็น
การฉายและรีเจกชันสามารถวางนัยทั่วไปได้กับเบลดศูนย์ โดยการเปลี่ยนตัวผกผัน ด้วยตัวผกผันเทียม เทียบกับผลคูณย่อ ผลลัพท์ของการฉายทับกันสนิททั้งสองกรณีสำหรับเบลดไม่เป็นศูนย์ สำหรับเบลดศูนย์ นิยามของการฉายที่ได้ให้มานี้ด้วยผลคูณย่อตัวแรกแทนที่จะเป็นตัวที่สองที่ซึ่งควรใช้ตัวผกผันเทียม เพราะเมื่อนั้นผลลัพท์จะจำเป็นต้องอยู่ในปริภูมิย่อยที่มี เป็นตัวแทน
การฉายวางนัยทั่วไปผ่านสภาพเชิงเส้นไปยังมัลติเวกเตอร์ทั่วไป การฉายจะไม่เป็นเชิงเส้นที่ และไม่สามารถวางนัยทั่วไปกับวัตถุ ที่ไม่ใช่เบลดได้
การสะท้อน
[แก้]การสะท้อนอย่างง่ายในระนาบเกินเขียนได้ง่ายในพีชคณิตนี้ผ่านการคอนจูเกตด้วยเวกเตอร์ สามารถก่อกำเนิดกรุปของการหมุนและการหมุนไม่ตรงแบบทั่วไป
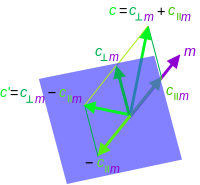
ภาพสะท้อน ของเวกเตอร์ ตามเวกเตอร์ หรือโดยสมมูล ในระนาบเกินตั้งฉากกับ ผลลัพธ์ของการสะท้อนจะเป็น
การหมุน
[แก้]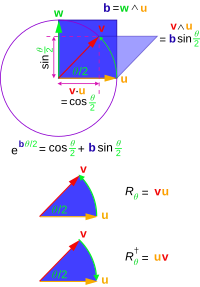
ถ้ามีผลคูณเวกเตอร์ แล้วจะเขียนการผันกลับได้เป็น
ให้เป็นตัวอย่าง สมมติว่า เราจะได้
ปรับขนาด เพื่อที่ แล้ว
ดังนั้น ไม่เปลี่ยนแปลงขนาดของ ยังสามารถแสดงได้ว่า
ดังนั้นการแปลง ทำให้ทั้งขนาดและมุม(ระหว่างเวกเตอร์)คงสภาพ จึงสามารถระบุได้ว่าเป็นการหมุนหรืแการหมุนไม่ตรงแบบ เรียก ว่าโรเตอร์ ถ้าเป็นการหมุนแท้ (ตามที่เป็นอยู่ถ้าสามารถเขียนได้อยู่ในรูปผลคูณของเวกเตอร์คู่ตัว) และเป็นตัวอย่างของสิ่งใน GA ที่เรียกว่าเวอร์เซอร์
มีวิธีทั่วไปในการหมุนเวกเตอร์ที่เกี่ยวข้องกับมัลติเวกเตอร์ในรูป ที่ก่อให้เกิดการหมุน ในระนาบและทิศทา่งกำหนดโดย-เบลด
โรเตอร์เป็นรูปทั่วไปของควอเทอร์เนีนรบนปริภูมิ-มิติ
ตัวอย่างและการประยุกต์ใช้
[แก้]ปริมาตรเกินของทรงสี่เหลี่ยมด้านขนานโดยเวกเตอร์
[แก้]สำหรับเวกเตอร์ และ ที่แผ่เป็นสี่เหลี่ยมด้านขนานจะได้
แคลคูลัสเชิงเรขาคณิต
[แก้]บทความหลัก แคลคูลัสเชิงเรขาคณิตพีชคณิตของปริภูมิกายภาพ
แคลคูลัสเชิงเรขาคณิตขยายรูปนัยนิยมเพื่อรวมการอนุพันธ์และการปริพันธ์รวมถึงเรขาคณิตเชิงอนุพันธ์และรูปแบบเชิงอนุพันธ์
โดยพื้นฐาน อนุพันธ์เวกเตอร์ได้นิยามเพื่อให้ทฤษฎีบทของกรีนในพีชคณิตเชิงเรขาคณิตเป็นจริง
จึงสามารถกล่าวได้ว่า
เป็นผลคูณเชิงเรขาคณิต วางนัยทั่วไปได้กับทฤษฎีบทของสโตรกส์อย่างมีผล (รวมทั้งในรูปแบบเชิงอนุพันธ์ด้วย)
ใน 1 มิติ เมื่อ เป็นเส้นโค้งที่มีจุดปลายเป็น และ แล้ว
จะย่อลงเป็น
หรือทฤษฎีมูลฐานของแตลคูลัสเชิงปริพันธ์
และที่ได้รับพัฒนาคือแนวคิดของแมนิโฟลด์เวกเตอร์และทฤษฎีการปริพันธ์เชิงเรขาคณิต(ที่วางนัยทั่วไปกับรูปแบบเชิงอนุพันธ์)
ประวัติ
[แก้]ดูเพิ่ม
[แก้]- เปรียบเทียบระหว่างพีชคณิตเวกเตอร์และพีชคณิตเชิงเรขาคณิต
- พีชคณิตแบบคลิฟฟอร์ด
- พีชคณิตแบบกรัสมัน-เคย์ลี
- พีชคณิตกาลา่กาศ
- สปิเนอร์
- ควอเทอร์เนียน
- พีชคณิตของปริภูมิกายภาพ
- พีชคณิตเชิงเรขาคณิตสากล
หมายเหตุ
[แก้]อ้างอิง
[แก้]แหล่งอ้างอิงและอ่านเพิ่มเติม
[แก้]- Arranged chronologically
- Grassmann, Hermann (1844), Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik: dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert, Leipzig: O. Wigand, OCLC 20521674
- Clifford, Professor (1878), "Applications of Grassmann's Extensive Algebra", American Journal of Mathematics, 1 (4): 350–358, doi:10.2307/2369379, JSTOR 2369379
- Artin, Emil (1988) [1957], Geometric algebra, Wiley Classics Library, Wiley, doi:10.1002/9781118164518, ISBN 978-0-471-60839-4, MR 1009557
- Hestenes, David (1966), Space–time Algebra, Gordon and Breach, ISBN 978-0-677-01390-9, OCLC 996371
- Wheeler, J. A.; Misner, C.; Thorne, K. S. (1973), Gravitation, W.H. Freeman, ISBN 978-0-7167-0344-0
- Bourbaki, Nicolas (1980), "Ch. 9 "Algèbres de Clifford"", Eléments de Mathématique. Algèbre, Hermann, ISBN 9782225655166
- Hestenes, David; Sobczyk, Garret (1984), Clifford Algebra to Geometric Calculus, a Unified Language for Mathematics and Physics, Springer Netherlands, ISBN 978-90-277-1673-6
- Hestenes, David (1986), "A Unified Language for Mathematics and Physics", ใน J.S.R. Chisholm; A.K. Commons (บ.ก.), Clifford Algebras and Their Applications in Mathematical Physics, NATO ASI Series (Series C), vol. 183, Springer, pp. 1–23, doi:10.1007/978-94-009-4728-3_1, ISBN 978-94-009-4728-3
- Wilmot, G.P. (1988a), The Structure of Clifford algebra. Journal of Mathematical Physics, vol. 29, pp. 2338–2345
- Wilmot, G.P. (1988b), "Clifford algebra and the Pfaffian expansion", Journal of Mathematical Physics, 29: 2346–2350, doi:10.1063/1.528118
- Chevalley, Claude (1991), The Algebraic Theory of Spinors and Clifford Algebras, Collected Works, vol. 2, Springer, ISBN 3-540-57063-2
- Doran, Chris J. L. (1994), Geometric Algebra and its Application to Mathematical Physics (PhD thesis), University of Cambridge, doi:10.17863/CAM.16148, hdl:1810/251691, OCLC 53604228
- Baylis, W. E., บ.ก. (2011) [1996], Clifford (Geometric) Algebra with Applications to Physics, Mathematics, and Engineering, Birkhäuser, ISBN 9781461241058
- Aragón, G.; Aragón, J.L.; Rodríguez, M.A. (1997), "Clifford Algebras and Geometric Algebra", Advances in Applied Clifford Algebras, 7 (2): 91–102, doi:10.1007/BF03041220, S2CID 120860757
- Hestenes, David (1999), New Foundations for Classical Mechanics (2nd ed.), Springer Verlag, ISBN 978-0-7923-5302-7
- Lasenby, Joan; Lasenby, Anthony N.; Doran, Chris J. L. (2000), "A Unified Mathematical Language for Physics and Engineering in the 21st Century" (PDF), Philosophical Transactions of the Royal Society A, 358 (1765): 21–39, Bibcode:2000RSPTA.358...21L, doi:10.1098/rsta.2000.0517, S2CID 91884543, เก็บ (PDF)จากแหล่งเดิมเมื่อ 2015-03-19
- Lounesto, Pertti (2001), Clifford Algebras and Spinors (2nd ed.), Cambridge University Press, ISBN 978-0-521-00551-7
- Baylis, W. E. (2002), Electrodynamics: A Modern Geometric Approach (2nd ed.), Birkhäuser, ISBN 978-0-8176-4025-5
- Dorst, Leo (2002), "The Inner Products of Geometric Algebra", ใน Dorst, L.; Doran, C.; Lasenby, J. (บ.ก.), Applications of Geometric Algebra in Computer Science and Engineering, Birkhäuser, pp. 35–46, doi:10.1007/978-1-4612-0089-5_2, ISBN 978-1-4612-0089-5
- Doran, Chris J. L.; Lasenby, Anthony N. (2003), Geometric Algebra for Physicists (PDF), Cambridge University Press, ISBN 978-0-521-71595-9, เก็บ (PDF)จากแหล่งเดิมเมื่อ 2009-01-06
- Hestenes, David (2003), "Oersted Medal Lecture 2002: Reforming the Mathematical Language of Physics" (PDF), Am. J. Phys., 71 (2): 104–121, Bibcode:2003AmJPh..71..104H, CiteSeerX 10.1.1.649.7506, doi:10.1119/1.1522700, เก็บ (PDF)จากแหล่งเดิมเมื่อ 2010-06-17
- Hildenbrand, Dietmar; Fontijne, Daniel; Perwass, Christian; Dorst, Leo (2004), "Geometric Algebra and its Application to Computer Graphics" (PDF), Proceedings of Eurographics 2004, doi:10.2312/egt.20041032, เก็บ (PDF)จากแหล่งเดิมเมื่อ 2015-09-06
- Lasenby, Anthony (2004), "Conformal Models of de Sitter Space, Initial Conditions for Inflation and the CMB", AIP Conference Proceedings, vol. 736, pp. 53–70, arXiv:astro-ph/0411579, doi:10.1063/1.1835174, S2CID 18034896
- Hestenes, David (2005), Introduction to Primer for Geometric Algebra
- Selig, J.M. (2005). Geometric Fundamentals of Robotics. Monographs in Computer Science (ภาษาอังกฤษ). New York, NY: Springer New York. doi:10.1007/b138859. ISBN 978-0-387-20874-9.
- Bain, J. (2006), "Spacetime structuralism: §5 Manifolds vs. geometric algebra", ใน Dennis Dieks (บ.ก.), The ontology of spacetime, Elsevier, p. 54 ff, ISBN 978-0-444-52768-4
- Dorst, Leo; Fontijne, Daniel; Mann, Stephen (2007), Geometric algebra for computer science: an object-oriented approach to geometry, Elsevier, ISBN 978-0-12-369465-2, OCLC 132691969
- Penrose, Roger (2007), The Road to Reality, Vintage books, ISBN 978-0-679-77631-4
- Francis, Matthew R.; Kosowsky, Arthur (2008), "The Construction of Spinors in Geometric Algebra", Annals of Physics, 317 (2): 383–409, arXiv:math-ph/0403040v2, Bibcode:2005AnPhy.317..383F, doi:10.1016/j.aop.2004.11.008, S2CID 119632876
- Li, Hongbo (2008), Invariant Algebras and Geometric Reasoning, World Scientific, ISBN 9789812770110. Chapter 1 as PDF
- Vince, John A. (2008), Geometric Algebra for Computer Graphics, Springer, ISBN 978-1-84628-996-5
- Lundholm, Douglas; Svensson, Lars (2009), "Clifford Algebra, Geometric Algebra and Applications", arXiv:0907.5356v1 [math-ph]
- Perwass, Christian (2009), Geometric Algebra with Applications in Engineering, Geometry and Computing, vol. 4, Bibcode:2009gaae.book.....P, doi:10.1007/978-3-540-89068-3, ISBN 978-3-540-89067-6
- Selig, J. M. (2000), "Clifford algebra of points, lines and planes" (PDF), Robotica, 18 (5): 545–556, doi:10.1017/S0263574799002568, S2CID 28929170
- Bayro-Corrochano, Eduardo (2010), Geometric Computing for Wavelet Transforms, Robot Vision, Learning, Control and Action, Springer Verlag, ISBN 9781848829299
- Bayro-Corrochano, E.; Scheuermann, Gerik, บ.ก. (2010), Geometric Algebra Computing in Engineering and Computer Science, Springer, ISBN 9781849961080 Extract online at http://geocalc.clas.asu.edu/html/UAFCG.html #5 New Tools for Computational Geometry and rejuvenation of Screw Theory
- Goldman, Ron (2010), Rethinking Quaternions: Theory and Computation, Morgan & Claypool, Part III. Rethinking Quaternions and Clifford Algebras, ISBN 978-1-60845-420-4
- Dorst, Leo.; Lasenby, Joan (2011), Guide to Geometric Algebra in Practice, Springer, ISBN 9780857298119
- Macdonald, Alan (2011), Linear and Geometric Algebra, CreateSpace, ISBN 9781453854938, OCLC 704377582
- Snygg, John (2011), A New Approach to Differential Geometry using Clifford's Geometric Algebra, Springer, ISBN 978-0-8176-8282-8
- Hildenbrand, Dietmar (2012), "Foundations of Geometric Algebra computing", Numerical Analysis and Applied Mathematics Icnaam 2012: International Conference of Numerical Analysis and Applied Mathematics, AIP Conference Proceedings, 1479 (1): 27–30, Bibcode:2012AIPC.1479...27H, doi:10.1063/1.4756054
- Sokolov, Andrey (2013), Clifford algebra and the projective model of Minkowski (Pseudo-Euclidean) spaces, arXiv:1307.4179
- Bromborsky, Alan (2014), An introduction to Geometric Algebra and Calculus (PDF), เก็บ (PDF)จากแหล่งเดิมเมื่อ 2019-10-15
- Klawitter, Daniel (2015), Clifford Algebras, doi:10.1007/978-3-658-07618-4, ISBN 978-3-658-07617-7
- Kanatani, Kenichi (2015), Understanding Geometric Algebra: Hamilton, Grassmann, and Clifford for Computer Vision and Graphics, CRC Press, ISBN 978-1-4822-5951-3
- Li, Hongbo; Huang, Lei; Shao, Changpeng; Dong, Lei (2015), "Three-Dimensional Projective Geometry with Geometric Algebra", arXiv:1507.06634v1 [math.MG]
- Hestenes, David (2017), "The Genesis of Geometric Algebra: A Personal Retrospective", Advances in Applied Clifford Algebras, 27: 351–379, doi:10.1007/s00006-016-0664-z, S2CID 253592888
- Dorst, Leo (2016), "3D Oriented Projective Geometry Through Versors of แม่แบบ:Tmath", Advances in Applied Clifford Algebras, 26 (4): 1137–1172, doi:10.1007/s00006-015-0625-y
- Lengyel, Eric (2016). Foundations of game engine development. Mathematics. Vol. 1. Lincoln, California: Terathon Software LLC. ISBN 978-0-9858117-4-7.
- Vaz, Jayme; da Rocha, Roldão (2016), An Introduction to Clifford Algebras and Spinors, Oxford University Press, Bibcode:2016icas.book.....V, ISBN 978-0-19-878292-6
- Easter, Robert Benjamin; Hitzer, Eckhard (2017), "Double Conformal Geometric Algebra", Advances in Applied Clifford Algebras, 27 (3): 2175–2199, doi:10.1007/s00006-017-0784-0, S2CID 253600526
- Du, Juan; Goldman, Ron; Mann, Stephen (2017), "Modeling 3D Geometry in the Clifford Algebra R(4, 4)", Advances in Applied Clifford Algebras, 27 (4): 3039–3062, doi:10.1007/s00006-017-0798-7, S2CID 253587390
- Bayro-Corrochano, Eduardo (2018). Computer Vision, Graphics and Neurocomputing. Geometric Algebra Applications. Vol. I. Springer. ISBN 978-3-319-74830-6.
- Breuils, Stéphane (2018). Structure algorithmique pour les opérateurs d'Algèbres Géométriques et application aux surfaces quadriques (PDF) (PHD). université-paris-est. เก็บ (PDF)จากแหล่งเดิมเมื่อ 2019-07-14.
- Lavor, Carlile; Xambó-Descamps, Sebastià; Zaplana, Isiah (2018). A Geometric Algebra Invitation to Space-Time Physics, Robotics and Molecular Geometry. Springer. pp. 1–. ISBN 978-3-319-90665-2.
- Hrdina, Jaroslav; Návrat, Aleš; Vašík, Petr (2018), "Geometric Algebra for Conics", Advances in Applied Clifford Algebras, 28 (3), doi:10.1007/s00006-018-0879-2, S2CID 125649450
- Breuils, Stéphane; Fuchs, Laurent; Hitzer, Eckhard; Nozick, Vincent; Sugimoto, Akihiro (2019), "Three-dimensional quadrics in extended conformal geometric algebras of higher dimensions from control points, implicit equations and axis alignment" (PDF), Advances in Applied Clifford Algebras, 29 (3), doi:10.1007/s00006-019-0974-z, S2CID 253597480
- Josipović, Miroslav (2019). Geometric Multiplication of Vectors: An Introduction to Geometric Algebra in Physics. Springer International Publishing;Birkhäuser. p. 256. ISBN 978-3-030-01756-9.
- Hadfield, Hugo; Lasenby, Joan (2020), "Constrained Dynamics in Conformal and Projective Geometric Algebra", Advances in Computer Graphics, Lecture Notes in Computer Science, vol. 12221, pp. 459–471, doi:10.1007/978-3-030-61864-3_39, ISBN 978-3-030-61863-6, S2CID 224820480
- Wu, Bofeng (2022), "A signature invariant geometric algebra framework for spacetime physics and its applications in relativistic dynamics of a massive particle and gyroscopic precession", Scientific Reports, 12 (1): 3981, arXiv:2111.07353, Bibcode:2022NatSR..12.3981W, doi:10.1038/s41598-022-06895-0, PMC 8901677, PMID 35256628
- Wilmot, G.P. (2023). "The Algebra Of Geometry". GitHub.

























































































