ความไวและความจำเพาะ
ความไวและความจำเพาะ เป็นค่าวัดทางสถิติที่ใช้ประเมินประสิทธิภาพของการทดสอบที่ให้ผลเป็นสองส่วน (เช่นเป็นบวกและลบ) โดย
- ความไว[1] (อังกฤษ: sensitivity) คือสัดส่วนของผลบวกที่เป็นจริงสำหรับภาวะนั้น ๆ (เช่น สัดส่วนของการตรวจพบโรคในผู้ที่ป่วยจริง) มีไวพจน์เป็นคำอื่น ๆ รวมทั้ง อัตราผลบวกจริง (true positive rate), recall, probability of detection ซึ่งใช้ในสาขาต่าง ๆ[2]
- ความจำเพาะ[3] (อังกฤษ: specificity) คือสัดส่วนของผลลบที่เป็นจริงสำหรับภาวะนั้น ๆ (เช่น สัดส่วนของการตรวจไม่พบโรคในผู้ที่ไม่ป่วย) มีไวพจน์เป็นคำอื่น ๆ รวมทั้ง อัตราผลลบจริง (true negative rate)
ความไวจึงมีประโยชน์ในการวินิจฉัยแยกกันผลลบปลอม (false negative) เพราะว่าการทดสอบยิ่งไวเท่าไร โอกาสการได้ผลลบ (เช่น การพบว่าไม่มีโรค) ที่ไม่เป็นจริง (เช่น บุคคลจริง ๆ มีโรค) ก็น้อยลงเท่านั้น และดังนั้น ถ้าความไวอยู่ที่ 100% โอกาสได้ผลลบปลอมก็อยู่ที่ 0%[4] และความจำเพาะจึงมีประโยชน์ในการยืนยันภาวะที่มี โดยกันผลบวกปลอม (false positive) เพราะว่าการทดสอบยิ่งจำเพาะเท่าไร โอกาสการได้ผลบวก (เช่น การพบว่ามีโรค) ที่ไม่เป็นจริง (เช่น บุคคลจริง ๆ ไม่มีโรค) ก็น้อยลงเท่านั้น และดังนั้น ถ้าความจำเพาะอยู่ที่ 100% โอกาสได้ผลบวกปลอมก็อยู่ที่ 0%[4]
ในการทดสอบหนึ่ง ๆ ปกติจะต้องแลกเปลี่ยนข้อดีข้อเสีย ยกตัวอย่างเช่น เพื่อความปลอดภัยของท่าอากาศยาน เครื่องตรวจโลหะอาจจะตั้งให้ส่งสัญญาณเตือนแม้สำหรับวัตถุที่เสี่ยงน้อย เช่น หัวเข็มขัดหรือลูกกุญแจ (คือการตรวจมีความจำเพาะต่ำ) เพื่อลดโอกาสเสี่ยงพลาดวัตถุอันตราย (คือการตรวจมีความไวสูง) การแลกเปลี่ยนข้อดีข้อเสียเช่นนี้สามารถแสดงในกราฟเส้นโค้ง receiver operating characteristic (ROC) การทดสอบที่สมบูรณ์จะไว 100% (เช่น คนป่วยทั้งหมดมีผลบวก) และจำเพาะ 100% (เช่น คนปกติทั้งหมดมีผลลบ) แต่ว่า โดยทฤษฎีแล้ว การทดสอบทุกอย่างจะมีขอบเขตความผิดพลาดต่ำสุดที่เรียกว่า Bayes error rate
นิยาม
[แก้]
|
ลองสมมุติว่ากำลังประเมินการทดสอบชนิดใหม่ที่ตรวจคัดกรองโรคชนิดหนึ่ง แต่ละคนที่ทดสอบจริง ๆ มีหรือไม่มีโรค ผลสอบอาจเป็นบวก คือจัดบุคคลว่ามีโรค หรือเป็นลบ คือจัดบุคคลว่าไม่มีโรค แต่ผลของแต่ละคนอาจจะไม่เหมือนกับภาวะจริง ๆ ดังนั้น จะมีกรณีต่าง ๆ 4 อย่าง คือ
- ผลบวกจริง (true positive) ผู้ป่วยตรวจพบว่ามีโรคอย่างถูกต้อง
- ผลบวกปลอม (false positive) คนปกติตรวจพบว่ามีโรคอย่างไม่ถูกต้อง
- ผลลบจริง (true negative) คนปกติตรวจพบว่าไม่มีโรคอย่างถูกต้อง
- ผลลบปลอม (false negative) คนป่วยตรวจพบว่าไม่มีโรคอย่างไม่ถูกต้อง
โดยทั่วไป Positive = identified และ negative = rejected ดังนั้น
- True positive = correctly identified
- False positive = incorrectly identified
- True negative = correctly rejected
- False negative = incorrectly rejected
เราจะพิจารณากลุ่มทดสอบที่มีผลบวกมีจำนวน P และผลลบมีจำนวน N เนื่องจากโรคบางอย่าง ผล 4 อย่างสามารถทำเป็นตาราง contingency table หรือ confusion matrix ดังต่อไปนี้
| ภาวะ/โรค (ตรวจด้วยการตรวจมาตรฐานสูงสุด) | ||||
| เป็นโรค | ไม่เป็นโรค | |||
| ผล การตรวจ |
ผล การตรวจ เป็นบวก |
ผลบวกจริง | ผลบวกลวง (ความผิดพลาดชนิดที่ 1) |
ค่าทำนายผลบวก = Σ ผลบวกจริง Σ ผลตรวจทั้งหมดที่เป็นบวก
|
| ผล การตรวจ เป็นลบ |
ผลลบลวง (ความผิดพลาดชนิดที่ 2) |
ผลลบจริง | ค่าทำนายผลลบ = Σ ผลลบจริง Σ ผลตรวจทั้งหมดที่เป็นลบ
| |
| ความไว = Σ ผลบวกจริง Σ ผู้ป่วยทั้งหมดที่เป็นโรค
|
ความจำเพาะ = Σ ผลลบจริง Σ ผู้ป่วยทั้งหมดที่ไม่เป็นโรค
| |||
ความไว
[แก้]ส่วนนี้ไม่มีการอ้างอิงจากเอกสารอ้างอิงหรือแหล่งข้อมูล โปรดช่วยพัฒนาส่วนนี้โดยเพิ่มแหล่งข้อมูลน่าเชื่อถือ เนื้อหาที่ไม่มีการอ้างอิงอาจถูกคัดค้านหรือนำออก |
ความไวหมายถึงสมรรถภาพของการทดสอบในการตรวจหาคนที่มีภาวะนั้น ๆ ในตัวอย่างของเรา ค่าความไวคือสัดส่วนของบุคคลที่ได้ผลบวกจากการทดสอบในบรรดาคนที่มีโรค ซึ่งเขียนเป็นสมการได้ดังต่อไปนี้
ผลลบจากการทดสอบที่ไวสูงจะมีประโยชน์ในการกันโรคออก (ruling out) คือเชื่อถือได้เมื่อผลเป็นลบ เพราะว่ามันไม่ค่อยวินิจฉัยผู้ที่มีโรคผิด การทดสอบที่ไว 100% จะตรวจเจอคนไข้ที่มีโรคทั้งหมดโดยให้ผลบวก ดังนั้น ผลลบจึงกันออกได้อย่างแน่นอนว่า คนไข้ไม่มีโรค แต่ผลบวกของการทดสอบที่ไวสูงไม่สามารถยืนยันว่ามีโรค (ruling in) คือ ลองสมมุติว่ามีการทดสอบ "ปลอม" ที่ออกแบบให้ออกแต่ผลบวกเท่านั้น ดังนั้น เมื่อทดสอบคนไข้ที่มีโรค คนไข้ทั้งหมดก็จะได้ผลบวก ซึ่งบ่งว่าการทดสอบมีความไว 100% แต่ว่า โดยนิยามแล้ว ค่าความไวไม่สามารถกันผลบวกปลอมได้ เพราะว่า การทดสอบปลอมก็จะออกผลบวกสำหรับคนปกติทั้งหมด ซึ่งบ่งว่าการทดสอบมีอัตราผลบวกปลอม 100% ทำให้ไม่มีประโยชน์อะไรในการตรวจจับ หรือยืนยันว่ามีโรค ความไวไม่ใช่อย่างเดียวกับความเที่ยง (precision) หรือค่าทำนายเมื่อผลเป็นบวก (positive predictive value) ซึ่งเป็นอัตราส่วนของผลบวกจริงต่อค่ารวมของผลบวกจริงกับผลบวกปลอม คือเป็นสัดส่วนของผลบวกจริงต่อประชากรที่แสดงผลบวก
การคำนวณค่าความไวไม่รวมผลการทดสอบที่คลุมเครือ ถ้าไม่สามารถทดสอบใหม่ได้ ตัวอย่างที่คลุมเครือไม่ควรจะรวมเข้าเพื่อวิเคราะห์ (โดยให้ระบุจำนวนตัวอย่างที่ยกเว้นเมื่อแสดงค่าความไว) หรือสามารถปฏิบัติเหมือนกับผลลบปลอม (ซึ่งจะเป็นการแสดงค่าต่ำสุดของความไว และดังนั้น อาจจะเป็นค่าประเมินที่น้อยเกินจริง)
ความจำเพาะ
[แก้]ความจำเพาะเป็นสมรรถภาพของการทดสอบในการตรวจหาบุคคลที่ไม่มีภาวะนั้น ๆ ลองพิจารณาตัวอย่างการทดสอบคนไข้ของเรา ค่าความจำเพาะของการทดสอบก็คือสัดส่วนของบุคคลปกติที่ไม่มีโรค ผู้จะทดสอบได้ผลลบ ซึ่งสามารถเขียนเป็นสมการ
การได้ผลบวกจากการทดสอบจำเพาะสูงมีประโยชน์ในการวินิจฉัยว่าเป็นโรค (ruling in) เพราะว่า การทดสอบนี้ไม่ค่อยให้ผลบวกในคนปกติ เมื่อผลทดสอบเป็นบวก การทดสอบที่จำเพาะ 100% แสดงว่า ทั้งหมดเป็นผู้ป่วยโดยไม่มีคนปกติ[7]
ผลลบในการทดสอบที่จำเพาะสูงจะไม่มีประโยชน์ในการกันโรคออก ลองสมมุติว่ามีการทดสอบ "ปลอม" ที่ออกแบบให้แสดงผลลบเท่านั้น ซึ่งเมื่อทดสอบคนปกติทุกคน ก็จะแสดงผลลบทุกคน และนี่ก็จะให้ค่าจำเพาะ 100% ต่อการทดสอบ แต่การทดสอบเดียวกันก็จะให้ผลลบต่อผู้ป่วยทั้งหมดเหมือนกัน ดังนั้น ก็จะมีอัตราอัตราผลลบปลอมที่ 100% ซึ่งไม่มีประโยชน์อะไรในการกันโรคออก (ruling out) ความจำเพาะโดยนิยามไม่สามารถกันผลลบปลอมได้ การทดสอบที่จำเพาะสูงจะมีอัตราความผิดพลาดชนิดที่ 1 ต่ำ
ตัวอย่างแสดงเป็นรูป
[แก้]-
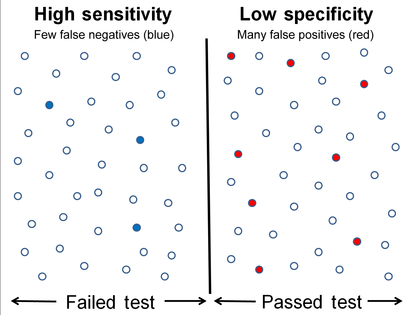
การทดสอบที่มีความไวสูงความจำเพาะต่ำ ซ้ายแสดงผลลบที่มีผลลบปลอม (น้ำเงินตัน) น้อย ขวาแสดงผลบวกที่มีผลบวกปลอม (แดง) มาก
-
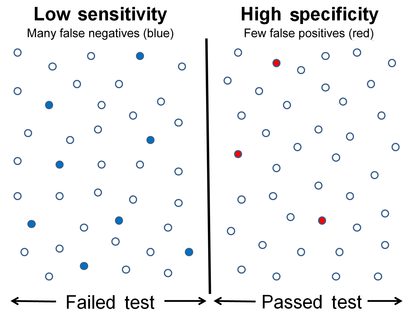
การทดสอบที่มีความไวต่ำความจำเพาะสูง ซ้ายแสดงผลบวกที่มีผลลบปลอม (น้ำเงินตัน) มาก ขวาแสดงผลบวกที่มีผลบวกปลอม (แดง) น้อย
ตัวอย่างในการแพทย์
[แก้]ในการวินิจฉัยทางการแพทย์ ความไวเป็นสมรรถภาพของการทดสอบในการระบุคนที่มีโรคอย่างถูกต้อง (อัตราผลบวกจริง) เทียบกับความจำเพาะที่เป็นสมรรถภาพในการระบุผู้ที่ไม่มีโรคอย่างถูกต้อง (อัตราผลลบจริง) ถ้ามีผู้ป่วย 100 คนที่ทดสอบ แต่มีเพียง 43 คนที่ได้ผลบวก การทดสอบนี้ก็จะมีความไว 43% ถ้ามีคนปกติ 100 คนที่ทดสอบ แต่มีคน 96 ที่ได้ผลลบ การทดสอบนี้ก็จะมีความจำเพาะ 96% ความไวและความจำเพาะเป็นคุณสมบัติของการทดสอบที่เป็นอิสระจากความชุกของโรค เพราะว่า ค่าของมันเฉพาะกับการทดสอบและไม่ได้ขึ้นอยู่กับความชุกของกลุ่มประชากรที่เป็นประเด็น[8] เทียบกับค่าทำนายเมื่อผลเป็นบวก (positive predictive value) และค่าทำนายเมื่อผลเป็นลบ (negative predictive value) ซึ่งเป็นค่าที่ขึ้นกับความชุกของกลุ่มประชากรที่ทดสอบ แต่ความจำเพาะและความไวไม่ใช่ ค่าเหล่านี้แสดงให้ดูเป็นกราฟในแอปเพล็ตนี้ (Bayesian clinical diagnostic model) ซึ่งแสดงค่าทำนายเมื่อผลเป็นบวกและเมื่อผลเป็นลบโดยเป็นฟังก์ชันของความชุกของโรค ความไว และความจำเพาะ
สิ่งที่อาจทำให้เข้าใจผิด
[แก้]มักกล่าวกันว่า การทดสอบที่จำเพาะสูงมีประโยชน์ในการยืนยันว่ามีโรคเมื่อได้ผลบวก และการทดสอบที่ไวสูงในการกันโรคออกเมื่อได้ผลลบ[9][10] มีแม้แต่รหัสช่วยจำ คือ SPIN และ SNOUT ที่ใช้กันอย่างกว้างขวาง ซึ่งมาจากวลีว่า a highly 'SPecific' test, when Positive, rules IN disease (SP-P-IN) คือ การทดสอบที่จำเพาะสูง เมื่อได้ผลบวก จะยืนยันโรค และจากวลีว่า a highly 'SeNsitive' test, when Negative rules OUT disease (SN-N-OUT) คือ การทดสอบที่ไวสูง เมื่อได้ผลลบ จะกันโรคออก แต่กฎทั้งสองนี้อาจทำให้เข้าใจเหตุผลผิดได้ เพราะว่า กำลังการวินิจฉัยของการทดสอบอย่างใดอย่างหนึ่งจะขึ้นอยู่กับทั้งความไวและความจำเพาะ[11][12][13]
ตารางแบบเติมตัวเลข
[แก้]- ตัวอย่างใส่ตัวเลขสำหรับการทดสอบวินิจฉัยที่มีความไว 67% และความจำเพาะ 91% เมื่อทดสอบกับบุคคล 2,030 คนเพื่อตรวจหาโรคที่มีความชุกในกลุ่มประชากรที่ 1.48%
| คนไข้ที่มีมะเร็งลำไส้ ดังที่ยืนยันโดย การส่องกล้อง (endoscopy) | ||||
| มีโรคจริง | ไม่มีโรค | |||
| ผลการ ตรวจเลือด ในอุจจาระ |
ผล บวก |
ผลบวกจริง (TP) = 20 |
ผลบวกปลอม (FP) = 180 |
ค่าทำนายเมื่อผล เป็นบวก (PPV) = TP / (TP + FP)
= 20 / (20 + 180) = 10% |
| ผล ลบ |
ผลลบปลอม (FN) = 10 |
ผลลบจริง (TN) = 1820 |
ค่าทำนายเมื่อผล เป็นลบ (NPV) = TN / (FN + TN)
= 1820 / (10 + 1820) ≈ 99.5% | |
| ความไว = TP / (TP + FN)
= 20 / (20 + 10) ≈ 67% |
ความจำเพาะ = TN / (FP + TN)
= 1820 / (180 + 1820) = 91% | |||
การคำนวณที่เกี่ยวข้อง
- False positive rate (α) = type I error = 1 − specificity = FP / (FP + TN) = 180 / (180 + 1820) = 9%
- False negative rate (β) = type II error = 1 − sensitivity = FN / (TP + FN) = 10 / (20 + 10) = 33%
- Power = sensitivity = 1 − β
- Likelihood ratio positive = sensitivity / (1 − specificity) = 0.67 / (1 − 0.91) = 7.4
- Likelihood ratio negative = (1 − sensitivity) / specificity = (1 − 0.67) / 0.91 = 0.37
เพราะมีผลบวกปลอมจำนวนมาก และผลลบปลอมจำนวนน้อย ดังนั้น การตรวจคัดกรองที่แสดงผลบวกอย่างเดียวจะไม่สามารถยืนยันว่ามีโรคได้ดี (PPV = 10%) และจึงต้องตรวจสอบเพิ่มขึ้น แต่ว่า มันก็ยังสามารถระบุคนที่มีโรคจริง ๆ ได้ถึง 66.7% (ซึ่งเป็นค่าความไว) ถึงอย่างนั้น ถ้าผลเป็นลบ มันดีมากที่จะยืนยันว่าคนไข้ไม่มีโรค (NPV = 99.5%) และการตรวจคัดกรองในเบื้องต้นที่ได้ผลลบจะระบุคน 91% ที่ไม่มีโรคได้อย่างถูกต้อง (ซึ่งเป็นค่าความจำเพาะ)
ค่าความไวและความจำเพาะเพียงอย่างเดียวอาจทำให้เข้าใจผิด คือ จะต้องคำนวณค่าแย่ที่สุด (worst-case) ของค่าทั้งสองเพื่อเลี่ยงการพึ่งผลการทดลองที่มีจำนวนน้อย ยกตัวอย่างเช่น การทดสอบหนึ่งไว 100% เมื่อเทียบกับวิธีการมาตรฐาน (gold standard) 4 ครั้ง แต่ว่าการทดสอบอีกครั้งหนึ่งแสดงผลที่ไม่เท่าเทียม คือเท่ากับแสดงความไวแค่ 80% วิธีสามัญอย่างหนึ่งก็คือมีการบ่ง binomial proportion confidence interval (คือ ช่วงความเชื่อมั่นในสัดส่วนหนึ่งของประชากรทางสถิติ) ซึ่งบ่อยครั้งคำนวณโดยใช้ Wilson score interval ดังนั้น ช่วงความเชื่อมั่น (confidence intervals) ของค่าความไวและความจำเพาะสามารถคำนวณได้ โดยให้พิสัยของค่า (คือกำหนดค่าสูงและต่ำ) ที่อยู่ในระดับความเชื่อมั่นขั้นหนึ่ง (เช่น ความเชื่อมั่นที่ 95% ว่าค่าอยู่ระหว่างค่านี้กับค่านี้)[14]
ศัพท์ในศาสตร์การค้นคืนสารสนเทศ
[แก้]ในการค้นคืนสารสนเทศ (information retrieval) ค่าทำนายเมื่อผลเป็นบวกเรียกว่า precision (ความเที่ยง) และค่าความไวเรียกว่า recall แต่ไม่เหมือนกับการแลกเปลี่ยนข้อดีข้อเสียระหว่างความจำเพาะเทียบกับความไว ค่าทั้งสองนี้เป็นอิสระจากผลลบจริง (true negative) ซึ่งปกติจะเป็นข้อมูลที่ไม่รู้โดยมีจำนวนมากกว่าจำนวนเอกสารที่เกี่ยวข้องและต้องการค้นคืนมาก และข้อสมมุติในเรื่องนี้ว่า ผลลบจริงเป็นจำนวนที่ใหญ่กว่ามากจะไม่ค่อยมีในการประยุกต์ใช้ค่าสองอย่างนี้ในประเด็นอื่น ๆ[6] จึงมีการใช้ F-score เป็นค่าเดียวที่แสดงประสิทธิภาพของการทดสอบที่ได้ผลบวก โดยเป็น harmonic mean ของ precision และ recall คือ
ศัพท์ในสถิติ
[แก้]ในการศึกษาโดยการตรวจสอบสมมติฐานทางสถิติ (statistical hypothesis testing) ความไวของการทดสอบจะเรียกว่า กำลังทางสถิติ (statistical power) ของการทดสอบ แต่คำว่า กำลัง (power) ในเรื่องนี้มีความหมายกว้างกว่าความไวที่ใช้ในบทความนี้ การทดสอบที่ไวจะมีความผิดพลาดชนิดที่ 2 จำนวนน้อยกว่า
ดูเพิ่ม
[แก้]เชิงอรรถและอ้างอิง
[แก้]- ↑ "sensitivity", ศัพท์บัญญัติอังกฤษ-ไทย, ไทย-อังกฤษ ฉบับราชบัณฑิตยสถาน (คอมพิวเตอร์) รุ่น ๑.๑ ฉบับ ๒๕๔๕,
(แพทยศาสตร์) ความไว
- ↑ "Detector Performance Analysis Using ROC Curves - MATLAB & Simulink Example". www.mathworks.com. สืบค้นเมื่อ 2016-08-11.
- ↑ "specificity", ศัพท์บัญญัติอังกฤษ-ไทย, ไทย-อังกฤษ ฉบับราชบัณฑิตยสถาน (คอมพิวเตอร์) รุ่น ๑.๑ ฉบับ ๒๕๔๕,
(แพทยศาสตร์) ความจำเพาะ
- ↑ 4.0 4.1 รองศาสตราจารย์ ดร. วารุณี เทศะกรณ์, ผู้ช่วยศาสตราจารย์ พญ. วิภา ธนาชาติเวทย์ (2554). ศาสตราจารย์แพทย์หญิงพรรณี ปิติสุทธิธรรม, รองศาสตราจารย์ ดร.ชยันต์ พิเชียรสุนทร (บ.ก.). "บทที่ 16 วิธีการตรวจวินิจฉัย" (PDF). ตำราการวิจัยทางคลินิก (Textbook of Clinical Research). มหาวิทยาลัยมหิดล. pp. 449–450. ISBN 978-974-11-1462-7. เก็บ (PDF)จากแหล่งเดิมเมื่อ 2015-07-07. สืบค้นเมื่อ 2016-12-19.
{{cite web}}: CS1 maint: uses authors parameter (ลิงก์) - ↑ Fawcett, Tom (2006). "An Introduction to ROC Analysis". Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010.
- ↑ 6.0 6.1 Powers, David M W (2011). "Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation" (PDF). Journal of Machine Learning Technologies. 2 (1): 37–63. คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2017-08-10. สืบค้นเมื่อ 2016-12-19.
- ↑ "SpPins and SnNouts". Centre for Evidence Based Medicine (CEBM). คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2014-07-20. สืบค้นเมื่อ 2013-12-026.
{{cite web}}: ตรวจสอบค่าวันที่ใน:|accessdate=(help) - ↑ Mangrulkar, Rajesh. "Diagnostic Reasoning I and II". คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2011-08-01. สืบค้นเมื่อ 2012-01-24.
- ↑ "Evidence-Based Diagnosis". Michigan State University. คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2013-07-06. สืบค้นเมื่อ 2016-12-19.
- ↑ "Sensitivity and Specificity". Emory University Medical School Evidence Based Medicine course.
- ↑
Baron, JA (Apr–Jun 1994). "Too bad it isn't true...". Medical decision making : an international journal of the Society for Medical Decision Making. 14 (2): 107. doi:10.1177/0272989X9401400202. PMID 8028462.
{{cite journal}}: CS1 maint: date format (ลิงก์) - ↑
Boyko, EJ (Apr–Jun 1994). "Ruling out or ruling in disease with the most sensitive or specific diagnostic test: short cut or wrong turn?". Medical decision making : an international journal of the Society for Medical Decision Making. 14 (2): 175–179. doi:10.1177/0272989X9401400210. PMID 8028470.
{{cite journal}}: CS1 maint: date format (ลิงก์) - ↑ Pewsner, D; Battaglia, M; Minder, C; Marx, A; Bucher, HC; Egger, M (2004-07-24). "Ruling a diagnosis in or out with "SpPIn" and "SnNOut": a note of caution". BMJ (Clinical research ed.). 329 (7459): 209–13. doi:10.1136/bmj.329.7459.209. PMC 487735. PMID 15271832.
- ↑ "Diagnostic test online calculator calculates sensitivity, specificity, likelihood ratios and predictive values from a 2x2 table - calculator of confidence intervals for predictive parameters". medcalc.org.
แหล่งข้อมูลอื่น
[แก้]- Altman, DG; Bland, JM (1994). "Diagnostic tests. 1: Sensitivity and specificity". BMJ. 308 (6943): 1552. doi:10.1136/bmj.308.6943.1552. PMC 2540489. PMID 8019315.
{{cite journal}}: CS1 maint: uses authors parameter (ลิงก์) - Loong, T (2003). "Understanding sensitivity and specificity with the right side of the brain". BMJ. 327 (7417): 716–719. doi:10.1136/bmj.327.7417.716. PMC 200804. PMID 14512479.
- UIC Calculator
- Vassar College's Sensitivity/Specificity Calculator
- MedCalc Free Online Calculator
- Bayesian clinical diagnostic model applet