ลวดลายในธรรมชาติ
ลิงก์ข้ามภาษาในบทความนี้ มีไว้ให้ผู้อ่านและผู้ร่วมแก้ไขบทความศึกษาเพิ่มเติมโดยสะดวก เนื่องจากวิกิพีเดียภาษาไทยยังไม่มีบทความดังกล่าว กระนั้น ควรรีบสร้างเป็นบทความโดยเร็วที่สุด |


ลวดลายในธรรมชาติ คือ รูปแบบที่มีความสม่ำเสมออย่างชัดเจนซึ่งพบได้ในโลกธรรมชาติ ลวดลายเหล่านี้เกิดขึ้นซ้ำ ๆ ในบริบทที่ต่างกัน และบางครั้งสามารถถูกกำหนดรูปแบบโดยแบบจำลองทางคณิตศาสตร์ ลวดลายทางธรรมชาติ ได้แก่ ความสมมาตร ต้นไม้ เกลียว ลำน้ำโค้งตวัด คลื่น โฟม เทสเซลเลชัน รอยแตก และ รอยริ้ว[1] นักปรัชญากรีกได้ศึกษาลวดลายเช่นเดียวกัน โดยมีเพลโต พีทาโกรัส และเอมเพโดคลีส พยายามจะอธิบายอันดับในธรรมชาติ การเข้าใจเรื่องลวดลายซึ่งมองเห็นได้นั้นได้รับการพัฒนาตามกาลเวลา
ในช่วงคริสต์ศตวรรษที่ 19 นักฟิสิกส์ชาวเบลเยี่ยม โยเซป พลาโตได้ทำการทดลองกับฟิล์มฟองสบู่ทำให้เขาได้วางเกณฑ์แนวความคิดของพื้นผิวที่น้อยที่สุด นักชีววิทยาและศิลปินชาวเยอรมัน แอร์นสต์ เฮคเคล ได้วาดรูปสัตว์น้ำกว่าร้อยชนิดเพื่อให้ความสำคัญเรื่องความสมมาตร นักชีววิทยาชาวสก๊อต D'Arcy Thompson ริเริ่มการศึกษาลวดลายในทั้งในพืชและสัตว์และแสดงให้เห็นว่าสามารถใช้สมการง่าย ๆ เพื่ออธิบายการโตแบบวงก้นหอยได้ ในช่วงคริสต์ศตวรรษที่ 20 นักคณิตศาสตร์ชาวอังกฤษ แอลัน ทัวริง ทำนายกลไกของการเกิดสัณฐานซึ่งทำให้เกิดลายจุดและรอยริ้ว นักชีววิทยาชาวฮังการี Aristid Lindenmayer และนักคณิตศาสตร์ชาวฝรั่งเศสอเมริกัน เบอนัว มานดัลบรอ แสดงว่าคณิตศาสตร์ของแฟร็กทัลสามารถสร้างลวดลายในการเจริญเติบโตของพืช
คณิตศาสตร์ ฟิสิกส์ และ เคมี สามารถอธิบายลวดลายในธรรมชาติในระดับที่ต่างกัน ลวดลายในสิ่งมีชีวิตอธิบายได้โดยวิธีทางชีววิทยาด้านการคัดเลือกโดยธรรมชาติ และ การคัดเลือกทางเพศ การศึกษาของการเกิดลวดลายแบบจำลองทางคอมพิวเตอร์เพื่อจำลองลวดลายในแบบต่าง ๆ
ประวัติ[แก้]

นักปรัชญากรีกในยุคแรกได้พยายามอธิบายอันดับในธรรมชาติ และคาดการแนวคิดสมัยใหม่ เพลโต (ประมาณ 427 – 347 ปีก่อนคริสต์ศักราช) โดยดูจากผลงานเกี่ยวกับลวดลายทางธรรมชาติของเขา เขาได้สนับสนุนการมีอยู่ของสิ่งสากล เขาเชื่อในการมีอยู่ของรูปแบบในอุดมคติ (εἶδος eidos: "form") ซึ่งกล่าวว่าวัตถุที่จับต้องได้ทุกอย่างนั้นไม่มีทางเป็นอะไรได้มากกว่าสำเนาที่บกพร่อง ดังนั้น ดอกไม้อาจมีรูปทรงกลม ทว่าไม่อาจเป็นวงกลมที่สมบูรณ์แบบทางคณิตศาสตร์ได้[2] พีทาโกรัส อธิบายลวดลายในธรรมชาติเสมือนการประสานเสียงในเสียงดนตรีซึ่งมาจากตัวเลขที่เขาเชื่อว่าเป็นองค์ประกอบพื้นฐานของการมีอยู่[3] เอมเพโดคลีสได้คาดการคำอธิบายทางวิวัฒนาการของสำหรับโครงสร้างสิ่งมีชีวิตของดาร์วินไว้ระดับหนึ่ง[4]
ในปีค.ศ. 1202 เลโอนาร์โด ฟีโบนัชชี (ประมาณปี ค.ศ. 1170–1250) ได้แนะนำลำดับจำนวนฟีโบนัชชีสู่โลกตะวันตกด้วยหนังสือของเขา Liber Abaci[5] ฟีโบนัชชีได้ให้ตัวอย่าง (ซึ่งเกินจริง) ทางชีววิทยาเกี่ยวกับการเติบโตของจำนวนประชากรกระต่ายในเชิงทฤษฎี[6] ในปีค.ศ. 1917 D'Arcy Wentworth Thompson (ปีค.ศ. 1860–1948) ตีพิมพ์หนังสือ On Growth and Form คำบรรยายเกี่ยวกับการจัดเรียงของใบไม้และลำดับฟีโบนัชชีของเขา หรือ ความสัมพันธ์เชิงคณิตศาสตร์ในการเติบโตแบบวงก้นหอยในพืช ได้รับการยกย้องว่ามีคุณภาพสูง เขาทำให้เห็นว่าสมการง่าย ๆ สามารถอธิบายการเติบโตแบบวงก้นหอยที่ซับซ้อนของเขาสัตว์และเปลือกของสัตว์ในไฟลัมมอลลัสกาได้[7]
นักฟิสิกส์ชาวเบลเยียม โยเซป พลาโต (ปี ค.ศ. 1801–1883) ได้สร้างปัญหาทางคณิตศาสตร์เรื่องการมีอยู่ของพื้นผิวที่น้อยที่สุดในพื้นที่ เขาศึกษาฟิล์มฟองสบู่และคิดค้นกฎของพลาโตซึ่งอธิบายเกี่ยวกับโครงสร้างของฟิล์มในฟองสบู่[8]
นักจิตวิทยาชาวเยอรมัน อดอล์ฟ ไซซิง (ปี ค.ศ. 1810–1876) อ้างว่าอัตราส่วนทองถูกแสดงในการเรียงตัวของส่วนของพืช ในโครงกระดูกของสัตว์และรูปแบบในการแตกออกของเส้นเลือดดำและเส้นประสาท รวมไปถึงในเรขาคณิตของผลึก[9][10][11]
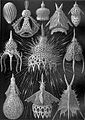
แอร์นสต์ เฮคเคล (ปีค.ศ. 1834–1919) ได้วาดรูปอันสวยงามของสิ่งมีชีวิตทางทะเลที่มีชื่อว่าแรดิโอลาเรียนโดยมุ่งเน้นไปที่ความสมมาตรเพื่อสนับสนุนทฤษฎีวิวัฒนาการดาร์วินอันผิดพลาดของเขา[12]
ช่างภาพชาวอเมริกัน วิลสัน เบนท์ลีย์ (ปี ค.ศ. 1865–1931) ถ่ายรูปภาพระดับจุลภาคของเกล็ดหิมะในปึค.ศ.1885[13]

ในปีค.ศ.1952 แอลัน ทัวริง (ปีค.ศ. 1912–1954) เป็นที่รู้จักจากงานเกี่ยวกับการคำนวณและการถอดรหัสหรือแปลข้อเขียนลับ ได้เขียนพื้นฐานเคมีของการเกิดสัณฐาน ซีงเป็นบทวิเคราะห์ของกลไกที่อาจจำเป็นในการสร้างลวดลายในสิ่งมีชีวิตในกระบวนการที่เรียกว่าการเกิดสัณฐาน[14] เขาได้ทำนายปฏิกิริยาแกว่งทางเคมีที่เรียกว่าปฏิกิริยาเบลูซอฟ–จาโบทินสกี ทัวริงเสนอว่า กลไกตัวเร่ง-ตัวยับยั้งเหล่านี้ สร้างลวดลายทางและลายจุดในสัตว์ และมีส่วนช่วยให้เกิดรูปแบบในการเรียงใบของพืช[15]
การเกิด[แก้]

สิ่งมีชีวิตเช่นกล้วยไม้ นกฮัมมิ่งเบิร์ด และหางของนกยูงมีการออกแบบที่เป็นนามธรรม โดยมีความงดงามของรูปแบบ ลวดลาย และสีซึ่งทำให้ศิลปินนั้นยากที่จะลอกเลียน[17] ความงดงามซึ่งผู้คนเห็นในธรรมชาติเกิดได้จากหลายอย่างด้วยกัน ทฤษฎีที่โดดเด่นได้แก่ คณิตศาสตร์ซึ่งควบคุมการเกิดของลวดลาย และในหมู่สิ่งมีชีวิตในผลของการคัดเลือกตามธรรมชาติซึ่งควบคุมวิธีซึ่งรูปแบบค่อยๆ พัฒนา[18]

รูปแบบของลวดลาย[แก้]
สมมาตร[แก้]
-
สัตว์มักแสดงการสมมาตรสองด้าน เช่นในเสือตัวนี้
-
สัตว์ในไฟลัมเอไคโนเตอร์มาตา เช่นปลาดาวตัวนี้มีความสมมาตรห้าพับ (fivefold symmetry)
-
ความสมมาตรห้าพับพบได้ในดอกไม้และผลไม้ เช่นผลพิกุลนี้
-
ผลึกหิมะมีความสมมาตรหกพับ
-
ผลึกหิมะแต่ละอันนั้นมีลักษณะเฉพาะแต่สมมาตร
-
ฟลูออไรต์ซึงมีรูปแบบของผลึกสี่เหลี่ยม
-
น้ำกระจายซึ่งมีรูปแบบสมมาตรรัศมี
-
การ์เนตซึ่งเป็นผลึกสี่เหลี่ยมข้าวหลามตัดสิบสองหน้า
-
วอลวอกซ์มีรูปแบบสมมาตรรัศมี
-
ดอกไม้ทะเลรูปแบบสมมาตรการหมุน
ต้นไม้ แฟร็กทัล[แก้]
-
ใบของพลาสลี่ (Anthriscus sylvestris) เรียงแบบขนนก 2 ถึง 3 ชั้น
-
แฟร็กทัลวงก้นหอย โรมาเนสโก้บรอกโคลีมีรูปแบบคล้ายตัวเอง
-
Angelica flowerhead ทรงกล้มสร้างจากทรงกลม (คล้ายตัวเอง)
-
ต้นไม้ รูปลิคเต็นเบิร์ก ไดอิเล็กทริกความแรงสูงทำลายบล็ออะคริลิค โพลิเมอร์ค
-
ต้นไม้ ผลึกทองแดงที่แตกแขนง (ใต้กล้องจุลทรรศน์)
-
รูปแบบการละลายน้ำแข็งแบบแฟร็กทัลบนดาวอังคาร
วงก้นหอย[แก้]
-
วงก้นหอยฟีโบนัชชี
-
แกะเขาใหญ่ (Ovis canadensis)
-
วงก้นหอย การจัดเรียงใบของ Aloe polyphylla
-
การเติบโตแบบลอการิทึมของเปลือกหอยนอติลุสเป็นวงก้นหอย
-
วงก้นหอยเฟอร์แม็ท หัวเมล็ดทานตะวัน (Helianthus annuus)
-
วงก้นหอยฟีโบนัชชีซ้อนกัน กะหล่ำแดงผ่ากลาง
-
เปลือกหอยทาก (Trochoidea liebetruti) แสดงให้เห็นถึงรูเปิดซึ่งขยับวนไปมา ไปข้างนอก และด้านล่าง เมื่อโตขึ้น
-
เปลือกหอยทากคล้ายกฎข้อที่ 30 ของ cellular automaton
-
Chaos: คลื่นวนของก้อนเมฆ
-
ทางน้ำโค้งตวัด และ ทะเลสาบรูปแอก (Oxbow lake) ใน Rio Negro เห็นได้จากอวกาศ
-
ทางน้ำโค้งตวัดที่ Rio Cauto ประเทศคิวบา
-
งูเลื้อยตวัด
-
ปะการังสมอง (Diploria strigosa)
คลื่น เนิน[แก้]
-
คลื่นในน้ำจากเรือ
-
เนินทรายในทะเลทรายทากลามากันจากอวกาศ
-
เนินทรายทรงจันทร์เสี้ยว
-
รอยคลื่นลมใน Sistan ประเทศอัฟกานิสถาน
ฟอง โฟม[แก้]
-
โฟมของฟองสบู่ ขอบทั้งสี่ด้านพบกันที่จุดเดียว ทำมุมใกล้เคียงกับ 109.5° เช่นเดียวกับพันธะ C-H ของ มีเทน
-
แรดิโอลาเรียนวาดโดยเฮคเคลใน Kunstformen der Natur (ปีค.ศ. 1904)
-
Haeckel's Spumellaria ของเฮคเคล โดยกระดูกของแรดิโอลาเรียนเหล่านี้มีรูปแบบคล้ายโฟม
-
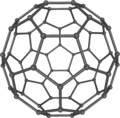
Buckminsterfullerene C60: Richard Smalley และคณะได้สังเคราะห์ฟูลเลอรีนในปีค.ศ.1985
-
Brochosomes (ไมโครพาติเคิลซึ่งผลิตโดยเพลี้ยจักจั่น) มักเรียนแบบรูปทรงทางเลขขาคณิตของฟูลเลอรีน
-
เต้นท์ละครสัตว์ใกล้เคียงกับพื้นผิวที่น้อยที่สุด
-
สระว่ายน้ำฟองน้ำสำหรับโอลิมปิกฤดูร้อน 2008
-
ทรงกลมขนาดเท่ากัน (ฟองแก๊ส) ในพื้นผิวของโฟม
เทสเซลเลชัน[แก้]
-
ผลึกทรงเหลี่ยมของแร่เฮไลท์
-
รังผึ้งในเทสเซลเลชัธรรมชาติ
-
ผลึก Bismuth hopper แสดงถึงรูปแบบผลึกแบบขั้นบันได
-
ดอกของ Fritillaria meleagris ซึ่งถูกเทสเซลเลชัน
-
เกล็ดที่ซ้อนกันของ Rutilus rutilus
-
เกล็ดซ้อนกันของสละ (Salacca zalacca)
-
ทางลาดยางเทสเซลเลชัน การจัดเรียงของหินที่หายากบนคาบสมุทรทัสมัน
รอยแตก[แก้]
-
พื้นผิวของเครื่องปั่นดินเผาโบราณซึ่งมีรอยแตก 90° องศา
-
โคลนแห้งซึ่งมีรอยแตก 90° เป็นส่วนใหญ่
-
หินแกบโบร ซึ่งมีรอยแตก 90°
-
โคลนแห้งซึ้งมีรอยแตก 120° เป็นส่วนใหญ่
-
หินบะซอลต์เย็น ซึ่งมีรอยแตก 120° เป็นส่วนใหญ่
-
ต้นปาล์มซึ่งมีรอยแตกแขนงแนวตั้ง (รอยแผลเป็นใบไม้แนวนอน)
ลายจุด ลายทาง[แก้]
-
ผีเสื้อ (Colobura dirce)
-
ม้าลาย (Equus grevyi)
-
ปลาสินสมุทรบั้งเหลือง (Pygoplites diacanthus)
-
เสือดาว (Panthera pardus pardus)
-
แมลงเต่าทอง โดย G.G. Jacobson
-
รูปแบบในการผสมพันธุ์ของหมึกกระดอง (Sepia officinalis)
การเกิดลวดลาย[แก้]
แอลัน ทัวริง[14] และนักชีวคณิตศาสตร์ เจมส์ เมอร์รี[19] ได้อธิบายกลไกซึ่งสร้างลายจุดหรือรอยริ้วได้โดยธรรมชาติ ที่เรียกว่าระบบปฏิกิริยา การแพร่ (reaction-diffusion system)[20] เซลล์ของสิ่งมีชีวิตระยะแรกเริ่มมียีนซึ่งสามารถสลับเปลี่ยนได้ด้วยสัญญาณทางเคมี หรือ มอร์โฟเจน (morphogen) ทำให้เกิดการเติบโตของรูปแบบเฉพาะ เช่นรอยสารสีเข้มบนผิวหนัง หากมอร์โฟเจนมีอยู่ทุกที่ ผลที่ได้คือการเกิดสีที่เสมอกัน เช่นในเสือดาวสีดำ ทว่าการกระจายไม่เสมอกันอาจทำให้เกิดจุดและลายทางได้ ทัวริงเสนอว่าอาจมีการควบคุมสัญญาณป้อนกลับ (feedback control) สำหรับการผลิตของตัวมอร์โฟเจนเอง สิ่งนี้อาจก่อให้เกิดความผันผวนอย่างต่อเนื่องในปริมาณมอร์โฟเจนขณะที่กำลังแพร่ทั่วร่างกาย กลไกที่สองเป็นที่ต้องการเพื่อสร้างลวดลายคลื่นนิ่ง (เพื่อให้เกิดลายจุดหรือลายทาง) ตัวยับยั้งทางเคมีซึ่งหยุดการทำงานของมอร์โฟเจน และซึ่งแพร่ผ่านร่างกายเร็วกว่ามอร์โฟเจน ทำให้เกิดแผนที่ประกอบด้วยตัวกระตุ้นและตัวยับยั้งและ ปฏิกิริยาเบลูซอฟ–จาโบทินสกีเป็นตัวอย่างที่ไม่เกี่ยวข้องทางชีววิทยาของแผนแบบนี้ หรือเรียกได้ว่าเป็น ตัวแกว่งทางเคมี (chemical oscillator)[20]
ต่อมา งานวิจัยได้สามารถสร้างแบบจำลองที่น่าเชื่อถือของลวดลายซึ่งครอบคลุมหลายอย่างเช่น ลายเส้นของม้าลาย แต้มบนยีราฟ จุดบนเสือจากัวร์ (แต้มสีเข้มปานกลางซึ่งล้อมรอบด้วยวงแหวนสีเข้มแตก ๆ) และลวดลายบนกระดองของแมลงเต่าทอง (รูปแบบทางเรขาคณิตต่าง ๆ ของลายจุดและลายทาง)[21] แบบจำลองการกระตุ้น-การยับยั้งของริชาร์ด พรัม ซึ่งพัฒนามาจากผลงานของทัวริง ใช้ตัวแปรหกตัวเพื่ออธิบายลวดลายพื้นฐานทั้งเก้า[22][23]:6
รูปแบบสามารถเกิดได้จากเหตุผลอื่นในภูมิภาพของพุ่มเสือ[24] andคลื่นต้นเฟอร์[25] ลายเส้นพุ่มเสือเกิดขึ้นบนที่ลาดเอียงที่มีความเอียงซึ่งการโตของพืชนั้นถูกจำกัดด้วยปริมาณฝน เส้นลายแนวนอนแต่ละเส้นที่พืชโตรวบรวมน้ำฝนจากพื้นที่ว่างข้างบนที่ติดกัน[24] คลื่นต้นเฟอร์เกิดขึ้นในป่าบนที่ลาดเอียงของภูเขาหลังการรบกวนของลมขณะกำลังเจริญทดแทน เมื่อต้นไม้ล้ม ต้นไม้ซึ่งต้นไม้ซึ่งเคยถูกปกป้องมีโอกาศที่จะถูกทำลายมากขึ้น ดังนั้นช่องว่างมีแน้วโน้มจะขยายตามทางลม ในขณะเดียวกัน บนด้านต้านลม ต้นกล้าโตและได้รับการปกป้องจากลมโดยต้นไม้ใหญ่[25] บางครั้ง ลวดลายทางธรรมชาติอาจเกิดจากสัตว์ เช่นในเนินมิมาในภาคตะวันตกเฉียงเหนือของสหรัฐอเมริกา และพื้นที่อื่น ซึ่งซึ่งสร้างโดย ตัวตุ่นดำดิน (gophers) โดยใช้เวลาหลายปี[26]
ในชั้นดินเยือกแข็งคงตัวซึ่งชั้นบนนั้นเกิดการแข็งตัวและละลายในทุกๆ ปี พื้นดินซึ่งมีลวดลายอาจเกิดขึ้น เป็นรูปทรงกลม ตาข่าย รูปหลายเหลี่ยมจากลิ่มน้ำแข็ง ขั้นบันได และลายทาง การหดตัวโดยความร้อนทำให้เกิดรอยแตก น้ำเติมเต็มรอยแตกเหล่านั้นขณะละลายและขยายตัวเมื่อแข็งเป็นลิ่ม รอยแตกเหล่านี้อาจเชื่อมกันเป็นรุปทรงหลายเหลี่ยหรือรูปทรงอื่น ๆ[27]
-
ปลาปักเป้ายักษ์ (Tetraodon mbu)
-
รายละเอียดบนผิวหนังปลาปักเป้ายักษ์
-
รูปถ่ายของการจำลองปฏิกิริยาเบลูซอฟ–จาโบทินสกี
-
ไก่ต๊อก (Numida meleagris) ซึ่งขนมีการเปลี่ยนรูปแบบจากแถบสีเป็นจุดทั้งบนเส้นขนและทั่วตัว
-
มุมบนของพุ่มเสือในประเทศไนเจอร์
-
คลื่นต้นเฟอร์ในภูเขาขาวรัฐนิวแฮมป์เชียร์
-
ดินบนน้ำแข็งที่กำลังละลายรายล้อมไปด้วยลิ่มน้ำแข็งใกล้รัฐ Tuktoyaktuk ประเทศแคนนาดา
ดูเพิ่ม[แก้]
อ้างอิง[แก้]
- ↑ Stevens, Peter.
- ↑ Balaguer, Mark (7 April 2009) [2004]. "Stanford Encyclopedia of Philosophy". Platonism in Metaphysics. Stanford University. สืบค้นเมื่อ 4 May 2012.
- ↑ The so-called Pythagoreans, who were the first to take up mathematics, not only advanced this subject, but saturated with it, they fancied that the principles of mathematics were the principles of all things.
- ↑ Aristotle reports Empedocles arguing that, "[w]herever, then, everything turned out as it would have if it were happening for a purpose, there the creatures survived, being accidentally compounded in a suitable way; but where this did not happen, the creatures perished."
- ↑ Singh, Parmanand.
- ↑ Knott, Ron. "Fibonacci's Rabbits". University of Surrey Faculty of Engineering and Physical Sciences.
- ↑ About D'Arcy.
- ↑ Stewart, Ian. 2001.
- ↑ Padovan, Richard (1999). Proportion. Taylor & Francis. pp. 305–306. ISBN 978-0-419-22780-9.
- ↑ Padovan, Richard (2002). "Proportion: Science, Philosophy, Architecture". Nexus Network Journal. 4 (1): 113–122. doi:10.1007/s00004-001-0008-7.
- ↑ Zeising, Adolf (1854). Neue Lehre van den Proportionen des meschlischen Körpers. preface.
- ↑ Ball, Philip.
- ↑ Hannavy, John (2007). Encyclopedia of Nineteenth-Century Photography. Vol. 1. CRC Press. p. 149. ISBN 0-415-97235-3.
- ↑ 14.0 14.1 Turing, A. M. (1952). "The Chemical Basis of Morphogenesis". Philosophical Transactions of the Royal Society B. 237 (641): 37–72. Bibcode:1952RSPTB.237...37T. doi:10.1098/rstb.1952.0012.
- ↑ Ball, Philip.
- ↑ Mandelbrot, Benoît B. (1983). The fractal geometry of nature. Macmillan.
- ↑ Forbes, Peter.
- ↑ Stevens, Peter. 1994.
- ↑ Murray, James D. (9 March 2013). Mathematical Biology. Springer Science & Business Media. pp. 436–450. ISBN 978-3-662-08539-4.
- ↑ 20.0 20.1 Ball, Philip.
- ↑ Ball, Philip.
- ↑ Rothenburg, David. 2011.
- ↑ Prum, Richard O.; Williamson, Scott (2002). "Reaction–diffusion models of within-feather pigmentation patterning" (PDF). Proceedings Royal Society London B. 269: 781–792. doi:10.1098/rspb.2001.1896.
- ↑ 24.0 24.1 Tongway, D.J.; Valentin, C. & Seghieri, J. (2001). Banded vegetation patterning in arid and semiarid environments. New York: Springer-Verlag.
- ↑ 25.0 25.1 D'Avanzo, C. (22 February 2004). "Fir Waves: Regeneration in New England Conifer Forests". TIEE. สืบค้นเมื่อ 26 May 2012.
- ↑ Morelle, Rebecca. "'Digital gophers' solve Mima mound mystery". BBC News. สืบค้นเมื่อ 9 December 2013.
- ↑ "Permafrost: Patterned Ground". US Army Corps of Engineers. คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2015-03-07. สืบค้นเมื่อ 17 February 2015.
บรรณานุกรม[แก้]
ผู้เขียนที่ริเริ่ม[แก้]
- Fibonacci, Leonardo. Liber Abaci, 1202.
- ----- translated by Sigler, Laurence E. Fibonacci's Liber Abaci. Springer, 2002.
- Haeckel, Ernst. Kunstformen der Natur (Art Forms in Nature), 1899–1904.
- Thompson, D'Arcy Wentworth. On Growth and Form. Cambridge, 1917.
หนังสือทั่วไป[แก้]
- Adam, John A. Mathematics in Nature: Modeling Patterns in the Natural World. Princeton University Press, 2006.
- Ball, Philip. Nature's Patterns: a tapestry in three parts. 1:Shapes. 2:Flow. 3:Branches. Oxford, 2009.
- Murphy, Pat and Neill, William. By Nature's Design. Chronicle Books, 1993.
- Rothenburg, David. Survival of the Beautiful: Art, Science and Evolution. Bloomsbury Press, 2011.
- Stevens, Peter S. Patterns in Nature. Little, Brown & Co, 1974.
- Stewart, Ian. What Shape is a Snowflake? Magical Numbers in Nature. Weidenfeld & Nicolson, 2001.
ลวดลายจากธรรมชาติ (เชิงศิลปะ)[แก้]
- Edmaier, Bernard. Patterns of the Earth. Phaidon Press, 2007.
- Macnab, Maggie. Design by Nature: Using Universal Forms and Principles in Design. New Riders, 2012.
- Nakamura, Shigeki. Pattern Sourcebook: 250 Patterns Inspired by Nature.. Books 1 and 2. Rockport, 2009.
- O'Neill, Polly. Surfaces and Textures: A Visual Sourcebook. Black, 2008.
- Porter, Eliot, and Gleick, James. Nature's Chaos. Viking Penguin, 1990.