ทรงตันอาร์คิมิดีส

ทรงตันอาร์คิมิดีส (Archimedean solid) หมายถึงทรงหลายหน้า (polyhedron) ที่เป็นทรงนูน (convex) โดยจุดยอดจุดหนึ่งจะประกอบด้วยหน้ารูปหลายเหลี่ยมปรกติ (regular polygon) ตั้งแต่สองชนิดขึ้นไป และเป็นชุดเดียวกันทุกจุด แตกต่างจากทรงตันเพลโต (Platonic solid) ตรงที่มีรูปหลายเหลี่ยมปรกติเพียงชนิดเดียว และแตกต่างจากทรงตันจอห์นสัน (Johnson solid) ตรงที่ไม่ได้มีรูปหลายเหลี่ยมบรรจบกันเป็นชุดเหมือนกันทุกจุด

ประเภท

ทรงตันอาร์คิมิดีส มีทั้งหมด 13 รูปทรง (หรืออาจนับเป็น 15 รูปทรงเนื่องจากเกลียวซ้ายขวาที่แตกต่างกัน) ตามตาราง

ชื่อ (โครงแบบจุดยอด)	ภาพโปร่ง	ภาพทึบ	ข่าย	หน้า		ขอบ	จุดยอด	Symmetry group
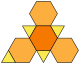
ทรงสี่หน้าปลายตัด (3.6.6)	(ภาพเคลื่อนไหว)			8	สามเหลี่ยม 4 หน้า หกเหลี่ยม 4 หน้า	18	12	Td
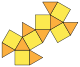
คิวบอกทาฮีดรอน (3.4.3.4)	(ภาพเคลื่อนไหว)			14	สามเหลี่ยม 8 หน้า สี่เหลี่ยม 6 หน้า	24	12	Oh
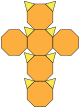
ทรงลูกบาศก์ปลายตัด หรือ ทรงหกหน้าปลายตัด (3.8.8)	(ภาพเคลื่อนไหว)			14	สามเหลี่ยม 8 หน้า แปดเหลี่ยม 6 หน้า	36	24	Oh
ทรงแปดหน้าปลายตัด (4.6.6)	(ภาพเคลื่อนไหว)			14	สี่เหลี่ยม 6 หน้า หกเหลี่ยม 8 หน้า	36	24	Oh
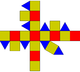
รอมบิคิวบอกทาฮีดรอน หรือ รอมบิคิวบอกทาฮีดรอนเล็ก (3.4.4.4)	(ภาพเคลื่อนไหว)			26	สามเหลี่ยม 8 หน้า สี่เหลี่ยม 18 หน้า	48	24	Oh
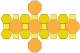
คิวบอกทาฮีดรอนปลายตัด หรือ รอมบิคิวบอกทาฮีดรอนใหญ่ (4.6.8)	(ภาพเคลื่อนไหว)			26	สี่เหลี่ยม 12 หน้า หกเหลี่ยม 8 หน้า แปดเหลี่ยม 6 หน้า	72	48	Oh
ทรงลูกบาศก์สนับ หรือ ทรงหกหน้าสนับ หรือ สนับคิวบอกทาฮีดรอน (2 รูปแบบเกลียว) (3.3.3.3.4)	(ภาพเคลื่อนไหว) (ภาพเคลื่อนไหว)			38	สามเหลี่ยม 32 หน้า สี่เหลี่ยม 6 หน้า	60	24	O
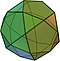
ทรงสามสิบสองหน้า (3.5.3.5)	(ภาพเคลื่อนไหว)			32	สามเหลี่ยม 20 หน้า ห้าเหลี่ยม 12 หน้า	60	30	Ih
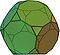
ทรงสิบสองหน้าปลายตัด (3.10.10)	(ภาพเคลื่อนไหว)			32	สามเหลี่ยม 20 หน้า สิบเหลี่ยม 12 หน้า	90	60	Ih
ทรงยี่สิบหน้าปลายตัด หรือ ฟูลเลอรีน หรือ ลูกฟุตบอล (5.6.6)	(ภาพเคลื่อนไหว)			32	ห้าเหลี่ยม 12 หน้า หกเหลี่ยม 20 หน้า	90	60	Ih
รอมบิโคซิโดเดคาฮีดรอน หรือ รอมบิโคซิโดเดคาฮีดรอนเล็ก (3.4.5.4)	(ภาพเคลื่อนไหว)			62	สามเหลี่ยม 20 หน้า สี่เหลี่ยม 30 หน้า ห้าเหลี่ยม 12 หน้า	120	60	Ih
ทรงสามสิบสองหน้าปลายตัด หรือ รอมบิโคซิโดเดคาฮีดรอนใหญ่ (4.6.10)	(ภาพเคลื่อนไหว)			62	สี่เหลี่ยม 30 หน้า หกเหลี่ยม 20 หน้า สิบเหลี่ยม 12 หน้า	180	120	Ih
ทรงสิบสองหน้าสนับ หรือ ทรงสามสิบสองหน้าสนับ (2 รูปแบบเกลียว) (3.3.3.3.5)	(ภาพเคลื่อนไหว) (ภาพเคลื่อนไหว)			92	สามเหลี่ยม 80 หน้า ห้าเหลี่ยม 12 หน้า	150	60	I

การสร้างทรงตันอาร์คิมิดีส

Construction of Archimedean Solids

สมมาตร		ทรงสี่หน้า	ทรงแปดหน้า		ทรงยี่สิบหน้า
รูปทรงตั้งต้น	Symbol {p,q}	ทรงสี่หน้า {3,3}	ลูกบาศก์ {4,3}	ทรงแปดหน้า {3,4}	ทรงสิบสองหน้า {5,3}	ทรงยี่สิบหน้า {3,5}
ตัดปลาย (t)	t{p,q}	ทรงสี่หน้าปลายตัด	ลูกบาศก์ปลายตัด	ทรงแปดหน้าปลายตัด	ทรงสิบสองหน้าปลายตัด	ทรงยี่สิบหน้าปลายตัด
ปรับตรง (r) Ambo (a)	r{p,q}	ทรงแปดหน้า	คิวบอกทาฮีดรอน		ทรงสามสิบสองหน้า
ตัดปลายคู่ (2t) Dual kis (dk)	2t{p,q}	truncated tetrahedron	ทรงแปดหน้าปลายตัด	truncated cube	ทรงยี่สิบหน้าปลายตัด	ทรงสิบสองหน้าปลายตัด
ปรับตรงคู่ (2r) รูปคู่ (d)	2r{p,q}	ทรงสี่หน้า	ทรงแปดหน้า	ลูกบาศก์	ทรงยี่สิบหน้า	ทรงสิบสองหน้า
ระเบิด (rr) Expansion (e)	rr{p,q}	คิวบอกทาฮีดรอน	รอมบิคิวบอกทาฮีดรอน		รอมบิโคซิโดเดคาฮีดรอน
Snub rectified (sr) Snub (s)	sr{p,q}	snub tetratetrahedron (icosahedron)	snub cuboctahedron		snub icosidodecahedron
Cantitruncation (tr) Bevel (b)	tr{p,q}	truncated tetratetrahedron (truncated octahedron)	truncated cuboctahedron		truncated icosidodecahedron

ดูเพิ่ม

• ทรงตันเพลโต
• ทรงหลายหน้าเอกรูป
• ทรงตันจอห์นสัน

อ้างอิง

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)

แหล่งข้อมูลอื่น

• เอริก ดับเบิลยู. ไวส์สไตน์, "Archimedean solid" จากแมทเวิลด์.
• Paper models of Archimedean solids
• Free paper models (nets) of Archimedean solids เก็บถาวร 2007-02-20 ที่ เวย์แบ็กแมชชีน
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
• Penultimate Modular Origami
• Interactive 3D polyhedra เก็บถาวร 2005-04-03 ที่ เวย์แบ็กแมชชีน in Java
• Contemporary Archimedean Solid Surfaces Designed by Tom Barber