ตัวแปรเสริมสโตกส์

ตัวแปรเสริมสโตกส์ I, Q, U และ V

ตัวแปรเสริมสโตกส์ (Stokes parameters) เป็นชุดของค่าสี่ค่าที่ใช้อธิบายสถานะของโพลาไรเซชัน ของคลื่นแม่เหล็กไฟฟ้า ตั้งชื่อตาม จอร์จ กาเบรียล สโตกส์ นักคณิตศาสตร์และนักฟิสิกส์ชาวไอร์แลนด์ ซึ่งเป็นผู้เสนอขึ้นในปี 1852

ตัวแปรเสริมเหล่านี้มักจะถูกเขียนในรูปแบบของเวกเตอร์ เรียกว่า เวกเตอร์สโตกส์ (Stokes vector) โดยแสดงเป็นฟังก์ชันของความเข้มรวมของลำแสง ระดับของโพลาไรเซชัน และตัวแปรเสริมที่เกี่ยวข้องกับรูปร่างเชิงวงรีของการโพลาไรซ์ ใช้เพื่ออธิบายแสงทั้งที่ไม่โพลาไรซ์ โพลาไรซ์บางส่วน และโพลาไรซ์ทั้งหมด ต่างจากวิธีการคำนวณของโจนส์ ซึ่งสามารถอธิบายได้เฉพาะแสงโพลาไรซ์ทั้งหมดเท่านั้น ยิ่งไปกว่านั้น การแทนด้วยค่านี้เหมาะสมอย่างยิ่งสำหรับการทดลอง เนื่องจากแต่ละค่าสอดคล้องกับผลรวมหรือความแตกต่างของความเข้มที่วัดได้ง่าย

ผลของระบบทางแสงที่มีต่อโพลาไรเซชันของแสงสามารถกำหนดได้โดยการสร้างเวกเตอร์สโตกส์สำหรับแสงที่ตกกระทบและใช้เมทริกซ์มึลเลอร์ เพื่อให้ได้เวกเตอร์สโตกส์ของแสงขาออกจากระบบ

หลักการ

เรามักจะนำตัวแปรเสริมสโตกส์มาเขียนรวมเป็นเวกเตอร์สโตกส์ ดังนี้:

${\vec {S}}\ ={\begin{pmatrix}S_{0}\\S_{1}\\S_{2}\\S_{3}\end{pmatrix}}={\begin{pmatrix}I\\Q\\U\\V\end{pmatrix}}$

เราสามารถมองว่าตัวแปรเสริมสโตกส์เป็นความเข้มทั่วไปสามค่า

• $I$: ความเข้มทั้งหมดที่วัดได้รวมกัน
• $V$: ความเข้มของโพลาไรเซชันแบบวงกลม ซึ่งอาจมีค่าเป็นบวกหรือลบขึ้นอยู่กับทิศทางของการหมุน
• $L\equiv Q+iU\equiv |L|e^{i2\theta }$: ความเข้มของโพลาไรเซชันแบบเส้นตรง ซึ่งเป็นจำนวนเชิงซ้อน ที่อธิบายความเอียง $\theta$ ของทิศทางของโพลาไรเซชัน

สำหรับแสงโพลาไรซ์ทั้งหมด ซึ่งมีสถานะโพลาไรซ์แบบเดียวกันทั้งหมด สามารถแสดงได้เป็น

${\begin{matrix}Q^{2}+U^{2}+V^{2}=I^{2}\end{matrix}}$

สำหรับลำแสงโพลาไรซ์บางส่วน ตัวแปรเสริมสโตกส์จะถูกกำหนดเป็นค่าเฉลี่ย สมการก่อนหน้าจะกลายเป็นอสมการ:

$Q^{2}+U^{2}+V^{2}=I_{p}^{2}\leq I^{2}.$

โดย $I_{p}/I$ เรียกว่าเป็น อัตราโพลาไรเซชัน

คำจำกัดความ

เราสามารถให้คำจำกัดความของตัวแปรเสริมสโตกส์ได้หลายแบบขึ้นอยู่กับว่าอธิบายสถานะของโพลาไรซ์ของแสงอย่างไร

คลื่นระนาบอาจแสดงลักษณะเฉพาะด้วยเวกเตอร์คลื่น ${\vec {k}}$ และแอมพลิจูดเชิงซ้อนของสนามไฟฟ้า $E_{1}$ และ $E_{2}$ อธิบายด้วยฐาน $({\hat {\epsilon }}_{1},{\hat {\epsilon }}_{2})$ หรืออาจแสดงโดยใช้เวกเตอร์คลื่น เฟส $\phi$ และสถานะโพลาไรเซชัน $\Psi$ โดย $\Psi$ คือเส้นโค้งที่วาด สนามไฟฟ้าในระนาบหนึ่ง ๆ สถานะโพลาไรเซชันที่พบบ่อยที่สุดคือโพลาไรเซชันแบบเส้นตรง และแบบวงกลม ซึ่งเป็นกรณีพิเศษของสถานะทั่วไปของโพลาไรเซชันแบบวงรี

องค์ประกอบสนามไฟฟ้า

ตัวแปรเสริมสโตกส์ถูกนิยามตามองค์ประกอบของสนามไฟฟ้าโดย

${\begin{matrix}I&\equiv &|E_{x}|^{2}+|E_{y}|^{2}\\&=&|E_{a}|^{2}+|E_{b}|^{2}\\&=&|E_{l}|^{2}+|E_{r}|^{2}\\Q&\equiv &|E_{x}|^{2}-|E_{y}|^{2}&\\U&\equiv &|E_{a}|^{2}-|E_{b}|^{2}&\\V&\equiv &|E_{l}|^{2}-|E_{r}|^{2}&\end{matrix}}$

โดยที่ดัชนีอ้างอิงถึงสามฐาน: ฐานอ้างอิงในระบบพิกัดคาร์ทีเซียน (${\hat {x}},{\hat {y}}$) ฐานที่ทำมุม 45 องศากับฐานอ้างอิง (${\hat {a}},{\hat {b}}$) และฐานวงกลม (${\hat {l}},{\hat {r}}$) โดยฐานวงกลมถูกกำหนดโดย ${\hat {l}}=({\hat {x}}+i{\hat {y}})/{\sqrt {2}}$

รูปทางขวาแสดงให้เห็นว่าเครื่องหมายบวกลบของตัวแปรเสริมสโตกส์มีความสัมพันธ์กับทิศทางการหมุนและการวางแนวของแกนเอกของวงรีอย่างไร

นอกจากนี้ยังสามารถแสดงตัวแปรเสริมสโตกส์ในทั้งสามฐานแต่ละฐานแยกกัน

ในฐาน (${\hat {x}},{\hat {y}}$) ตัวแปรเสริมสโตกส์ถูกนิยามโดย

${\begin{matrix}I&=&|E_{x}|^{2}+|E_{y}|^{2}\\Q&=&|E_{x}|^{2}-|E_{y}|^{2}\\U&=&2{\mbox{Re}}(E_{x}E_{y}^{*})\\V&=&-2{\mbox{Im}}(E_{x}E_{y}^{*})\\\end{matrix}}$

ในฐาน $({\hat {a}},{\hat {b}})$ แสดงได้เป็น

${\begin{matrix}I&=&|E_{a}|^{2}+|E_{b}|^{2}\\Q&=&-2{\mbox{Re}}(E_{a}^{*}E_{b})\\U&=&|E_{a}|^{2}-|E_{b}|^{2}\\V&=&2{\mbox{Im}}(E_{a}^{*}E_{b})\\\end{matrix}}$

และในฐาน $({\hat {l}},{\hat {r}})$:

${\begin{matrix}I&=&|E_{l}|^{2}+|E_{r}|^{2}\\Q&=&2{\mbox{Re}}(E_{l}^{*}E_{r})\\U&=&-2{\mbox{Im}}(E_{l}^{*}E_{r})\\V&=&|E_{l}|^{2}-|E_{r}|^{2}\\\end{matrix}}$

ในรูปของวงรี

วงรีของโพลาไรเซชันและตัวแปรที่เกี่ยวข้อง

วิธีหนึ่งในการอธิบายโพลาไรเซชันคือการระบุแกนเอกและแกนโทของวงรีโพลาไรเซชัน การวางแนว และทิศทางการหมุน ความสัมพันธ์ระหว่างค่าต่าง ๆ ในของวงรีโพลาไรเซชันกับตัวแปรเสริมสโตกส์ อาจแสดงได้ดังนี้:

${\begin{matrix}I_{p}&=&A^{2}+B^{2}\\Q&=&(A^{2}-B^{2})\cos(2\theta )\\U&=&(A^{2}-B^{2})\sin(2\theta )\\V&=&2ABh\\\end{matrix}}$

และในทางกลับกัน:

${\begin{matrix}A&=&{\sqrt {{\frac {1}{2}}(I_{p}+|L|)}}\\B&=&{\sqrt {{\frac {1}{2}}(I_{p}-|L|)}}\\\theta &=&{\frac {1}{2}}\arg(L)\\h&=&\operatorname {sgn}(V).\\\end{matrix}}$

ในพิกัดทรงกลม

วงรีโพลาไรเซชัน แสดงความสัมพันธ์ระหว่างทรงกลมปวงกาเรกับค่า ψ และ χ

ตัวแปรเสริมสโตกส์อาจแสดงในรูปของพิกัดทรงกลม เรียกว่าทรงกลมปวงกาเร

${\begin{aligned}S_{0}&=I\\S_{1}&=Ip\cos 2\psi \cos 2\chi \\S_{2}&=Ip\sin 2\psi \cos 2\chi \\S_{3}&=Ip\sin 2\chi \end{aligned}}$

ในที่นี้ $Ip$, $2\psi$ และ $2\chi$ คือพิกัดทรงกลมของสถานะโพลาไรเซชันในปริภูมิสามมิติของตัวแปรเสริมสโตกส์สามตัวหลัง ตัวคูณ 2 อยู่ข้างหน้า $\psi$ แสดงถึงความจริงที่ว่าวงรีที่หมุนไป 180 องศาจะไม่ต่างจากเดิม ในขณะที่ตัวคูณ 2 ที่อยู่ข้างหน้า $\chi$ บ่งบอกว่าวงรีจะไม่สามารถแยกความแตกต่างได้เมื่อพลิกแกนทั้งสองตามด้วยการหมุน 90

สามารถหาค่าต่าง ๆ ในพิกัดทรงกลมจากตัวแปรเสริมสโตกส์ได้ด้วยสมการต่อไปนี้:

${\begin{aligned}I&=S_{0}\\p&={\frac {\sqrt {S_{1}^{2}+S_{2}^{2}+S_{3}^{2}}}{S_{0}}}\\2\psi &=\mathrm {atan} {\frac {S_{2}}{S_{1}}}\\2\chi &=\mathrm {atan} {\frac {S_{3}}{\sqrt {S_{1}^{2}+S_{2}^{2}}}}\\\end{aligned}}$

ตัวอย่าง

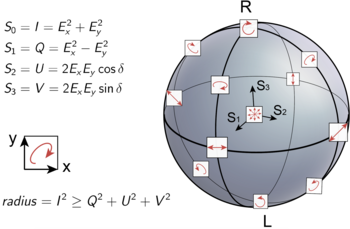ภาพอธิบายสถานะโพลาไรซ์บนทรงกลมปวงกาเร

ตารางต่อไปนี้แสดงเวกเตอร์สโตกส์สำหรับสถานะโพลาไรเซชันของแสงที่พบได้บ่อย

โพลาไรเซชัน	เวกเตอร์สโตกส์	โพลาไรเซชัน	เวกเตอร์สโตกส์
เส้นตรงแนวนอน	${\begin{pmatrix}1\\1\\0\\0\end{pmatrix}}$	เส้นตรงแนวตั้ง	${\begin{pmatrix}1\\-1\\0\\0\end{pmatrix}}$
วงกลมวนซ้าย	${\begin{pmatrix}1\\0\\0\\-1\end{pmatrix}}$	วงกลมวนขวา	${\begin{pmatrix}1\\0\\0\\1\end{pmatrix}}$
เส้นตรงเฉียง $\pm 45$ องศา	${\begin{pmatrix}1\\0\\\pm 1\\0\end{pmatrix}}$	ไม่โพลาไรซ์	${\begin{pmatrix}1\\0\\0\\0\end{pmatrix}}$