ผู้ใช้:Prame tan/พีชคณิตเชิงเรขาคณิต

พื้นผิว Togliatti เป็นพื้นผิวพีชคณิตที่มีดีกรีเท่ากับระดับห้า รูปนี้จำลองส่วนหนึ่งของโลคัสค่าจริงของพื้นผิวดังกล่าว

 เรขาคณิตเชิงพีชคณิต เป็นสาขาหนึ่งของ คณิตศาสตร์ ที่เริ่มแรกศึกษารากของพหุนามหลายตัวแปร เรขาคณิตเชิงพีชคณิตสมัยใหม่อาศัยวิธีการทางพีชคณิตนามธรรม โดยเฉพาะอย่างยิ่งเครื่องมือจากพีชคณิตสลับที่เพื่อใช้การแก้ปัญหาทางเรขาคณิตเกี่ยวกับเซตของรากของพหุนามดังกล่าว

วัตถุพื้นฐานของการศึกษาในเรขาคณิตเชิงพีชคณิตคือวาไรตีเชิงพีชคณิต ซึ่งเป็นผลเฉลยของระบบสมการพหุนามผ่านมุมมองเชิงเรขาคณิต ตัวอย่างวาไรตีเชิงพีชคณิตที่ได้รับการศึกษามากที่สุด เช่น เส้นโค้งเชิงพีชคณิตระนาบ ซึ่งรวมถึง เส้น วงกลม พาราโบลา วงรี ไฮเพอร์โบลา, เส้นโค้งคิวบิก เช่น เส้นโค้งเชิงวงรี และเส้นโค้งควอร์ติกเช่น เลมนิสเคต และ วงรีแคสสินี

ประเด็นพื้นฐานของเรขาคณิตเชิงพีชคณิตคือศึกษาจุดประเภทหนึ่งบนเส้นโค้งเชิงวงรีที่มีสมบัติน่าสนใจเป็นพิเศษ เช่น จุดเอกฐาน จุดเปลี่ยนความเว้า และจุดที่อนันต์ ในขณะที่ปัญหาขั้นสูงนั้นเชื่อมโยงไปยังโทโพโลยีของเส้นโค้งและความสัมพันธ์ระหว่างเส้นโค้งที่กำหนดโดยสมการที่แตกต่างกัน

เรขาคณิตเชิงพีชคณิตเป็นหัวใจสำคัญของคณิตศาสตร์สมัยใหม่ และมีความเชื่อมโยงไปยังสาขาต่าง ๆ อย่างหลากหลาย เช่น การวิเคราะห์เชิงซ้อน ทอพอโลยี และ ทฤษฎีจำนวน

ในศตวรรษที่ 20 เรขาคณิตเชิงพีชคณิตได้แยกย่อยของเป็นสาขาย่อยจำนวนมาก

แนวคิดพื้นฐาน

รากของระบบพหุนาม

ทรงกลมและวงกลมเอียง

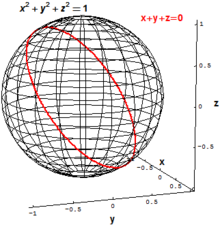
ในเรขาคณิตเชิงพีชคณิตคลาสสิก นักคณิตศาสตร์ศึกษาเซตของจุดที่เป็นรากของระบบสมการพหุนามรูปแบบหนึ่ง ตัวอย่างเช่น ทรงกลมในสองมิติที่มีรัศมีเท่ากับ 1 ใน ปริภูมิแบบยุคลิดสามมิติ R³ อาจนิยามให้เป็นเซตของจุด (x,y,z) ทั้งหมดที่ทำให้

$x^{2}+y^{2}+z^{2}-1=0.\,$

วงกลม"เอียง" ใน R³ สามารถกำหนดให้เป็นเซตของจุด (x,y,z) ทั้งหมด ที่สอดคล้องกับระบบสมการพหุนามสองสมการ

${\begin{cases}x^{2}+y^{2}+z^{2}-1=0\\x+y+z=0\end{cases}}$

วาไรตีสัมพรรค

กำหนดฟิลด์ $k$ ในเรขาคณิตเชิงพีชคณิตคลาสสิกนิยมให้ฟิลด์นี้เป็นฟิลด์จำนวนเชิงซ้อน C เสมอ แต่เราสามารถเปลี่ยน C เป็นฟีลด์ปิดเชิงพีชคณิตใด ๆ ได้ และทฤษฎียังคงเป็นจริง

เราพิจารณา ปริภูมิสัมพรรค (affine space) ในมิติเท่ากับ n เหนือฟิลด์ k ซึ่งเขียนแทนด้วย $\mathbf {A} ^{n}(k)$ (บางครั้งเขียน $\mathbf {A} ^{n}$ เมื่อ $k$ ชัดเจนจากบริบท) หากเรากำหนดระบบพิกัดฉากให้ $\mathbf {A} ^{n}(k)$ เราสามารถระบุ $\mathbf {A} ^{n}(k)$ ว่าเป็น $k^{n}$ เหตุผลที่เราไม่พิจารณา $k^{n}$ โดยตรงก็เพื่อลืมว่า $k^{n}$ มีโครงสร้างเป็นปริภูมิเวกเตอร์

จะเรียกฟังก์ชัน $f\colon \mathbf {A} ^{n}\to \mathbf {A} ^{1}$ ว่าเป็น ฟังก์ชันพหุนาม (หรือ ฟังก์ชันปกติ) หากสามารถเขียนเป็นพหุนามได้ นั่นคือถ้ามีพหุนาม p ใน k [ x ₁, ..., x _n ] เช่น ที่ f ( M ) = p ( t ₁, ..., t _n ) สำหรับทุกจุด M ที่ มีพิกัด ( t ₁, ..., t _n ) ใน A ⁿ คุณสมบัติของฟังก์ชันที่จะเป็นพหุนาม (หรือปกติ) ไม่ได้ขึ้นอยู่กับการเลือกระบบพิกัดใน Aⁿ

$V(S)=\{(t_{1},\dots ,t_{n})\mid p(t_{1},\dots ,t_{n})=0{\text{ for all }}p\in S\}.\,$

เซตเชิงพีชคณิตจะเป็น เซตลดทอนไม่ได้ หากมันไม่เป็นยูเนียนของเซตเชิงพีชคณิตที่เล็กกว่าสองเซตได้ เราพบว่า เซตเชิงพีชคณิตใด ๆ อยู่ในรูปยูเนียนจำกัดของเซตเชิงพีชคณิตที่ลดรูปไม่ได้ และการแยกส่วนดังนี้มีได้แบบเดียว ดังนั้นองค์ประกอบของมันจึงถูกเรียกว่า ส่วนประกอบที่ไม่สามารถลดทอนได้ ของเซตพีชคณิต เซตเชิงพีชคณิตที่ลดทอนไม่ได้เรียกอีกอย่างว่า วาไรตี

มีทฤษฎีว่า เซตเชิงพีชคณิตจะเป็นวาไรตีก็ต่อเมื่อ มีไอดีลเฉพาะของริงพหุนามหนึ่ง ที่ทำให้เซตเชิงพีชคณิตนั้นเป็นเซตของรากของไอดีล

ฟังก์ชันปกติ

เราทราบแล้วว่าฟังก์ชันต่อเนื่องเป็นการส่งธรรมชาติบนปริภูมิเชิงทอพอโลยี และฟังก์ชันเรียบเป็นการส่งธรรมชาติบนแมนิโฟลด์หาอนุพันธ์ได้ สำหรับเซตเชิงพีชคณิตก็มีฟังก์ชันประเภทหนึ่ง เรียกว่า ฟังก์ชันปกติ หรือ ฟังก์ชันเชิงพหุนาม

ฟังก์ชันปกติของเซตเชิงพีชคณิต V ที่เป็นส่วนอยู่ใน Aⁿ คือข้อ จำกัด ของ V ของฟังก์ชันปกติบน A ⁿ สำหรับชุดพีชคณิตที่กำหนดไว้ในฟิลด์ของจำนวนเชิงซ้อนฟังก์ชันปกติจะราบรื่นและแม้กระทั่ง การวิเคราะห์

มุมมองสมัยใหม่

วิธีการสมัยใหม่ในสาขาเรขาคณิตเชิงพีชคณิต ได้นิยามแนวคิดพื้นฐานจำนวนมากใหม่ ให้มีความเป็นนัยทั่วไปมากยิ่งขึ้น ตัวอย่างวัตถุที่เป็นที่สนใจเช่น สกีม สกีมรูปนัย อินด์-สกีม ปริภูมิเชิงพีชคณิต สแต็กเชิงพีชคณิต เป็นต้น เหตุผลที่ต้องขยายนัยทั่วไปเป็นเพราะว่าทฤษฎีของวาไรตี เช่น ฟังก์ชันรูปนัยของซาริสกี

ประวัติศาสตร์

ศตวรรษที่ 20

วาน เดอร์ วาร์เดน ออสการ์ ซาริสกี และ อองเดร์ แวย์ พัฒนารากฐานสำหรับเรขาคณิตเชิงพีชคณิตโดยอาศัย พีชคณิตสลับที่ร่วมสมัย รวมถึง ทฤษฎีแวลิวเอชัน และทฤษฎีของไอดีล เป้าหมายประการหนึ่งเพื่อสร้างโครงร่างที่รัดกุมในการพิสูจน์ผลลัพธ์จากเรขาคณิตเชิงพีชคณิตสกุลอิตาลี ทั้งนี้เพราะว่า นักคณิตศาสตร์ในสกุลนี้ใช้แนวคิดเรื่อง จุดทั่วไป ในงานคณิตศาสตร์โดยไม่มีคำจำกัดความที่ชัดเจน นิยามจุดทั่วไปกำหนดเป็นครั้งแรกโดยนักคณิตศาสตร์ข้างต้นในช่วงทศวรรษ 1930

ในช่วงทศวรรษที่ 1950 และ 1960 ฌ็อง-ปิแยร์ แซร์ และ อเล็กซองดร์ โกรเธนดีก สร้างรากฐานใหม่โดยใช้ ทฤษฎีชีฟ ในภายหลังโกรเธนดีกได้ริเริ่มเสนอแนวคิดเกี่ยวกับ สกีม ร่วมกับวิธีการทางฮอมอโลยี

วาไรตีที่สำคัญรูปแบบหนึ่งคือ วาไรตีอาบีเลียน ซึ่งเป็นวาไรตีเชิงภาพฉายที่มีจุดบนวาไรตีนี้เป็นกรุปอาบีเลียน ตัวอย่างต้นแบบของวาไรตีอาบีเลียนคือ เส้นโค้งเชิงวงรี ซึ่งมีทฤษฎีที่เกี่ยวข้องมากมาย เส้นโค้งเชิงวงรีเป็นเครื่องมือในการพิสูจน์ทฤษฎีบทสุดท้ายของแฟร์มาต์ และยังใช้ใน การเข้ารหัสเส้นโค้งเชิงวงรีอีกด้วย [[หมวดหมู่:สาขาของคณิตศาสตร์]]