ผิวกำลังสอง

ผิวกำลังสอง หรือ ควอดริก (อังกฤษ: quadric surface) ในทางคณิตศาสตร์ หมายถึง ผิว (hypersurface) ใน D มิติ ซึ่งกำหนดโดยคำตอบหรือทางเดินรากของสมการพหุนามกำลังสอง (quadratic polynomial) ถ้าเราพิจารณาพิกัด $\{x_{0},x_{1},x_{2},\ldots ,x_{D}\}$ ผิวกำลังสองถูกกำหนดด้วยสมการพีชคณิตดังต่อไปนี้

$\sum _{i,j=0}^{D}Q_{i,j}x_{i}x_{j}+\sum _{i=0}^{D}P_{i}x_{i}+R=0$

โดย Q คือ เมทริกซ์ มิติ D+1 และ P คือ เวกเตอร์ มิติ D+1 และ R คือ ค่าคงที่ ค่าของ Q, P และ R มักกำหนดเป็นจำนวนจริงหรือจำนวนเชิงซ้อน แต่อาจเป็นค่าฟีลด์ใด ๆ โดยทั่วไปแล้วคำตอบหรือทางเดินรากของกลุ่มของพหุนามนั้นเรียกว่าประเภทเชิงพีชคณิต (algebraic variety) ซึ่งเป็นสาขาหนึ่งของเรขาคณิตเชิงพีชคณิต (algebraic geometry) ควอดริกนั้นเป็นประเภทหนึ่งของประเภทเชิงพีชคณิต และประเภทของภาพฉายนั้นจะสมสัณฐานกับการตัดกันของควอดริก

สมการบรรทัดฐานของผิวกำลังสองใน 3 มิติ และมีจุดศูนย์กลางที่ (0,0,0) คือ

$\pm {x^{2} \over a^{2}}\pm {y^{2} \over b^{2}}\pm {z^{2} \over c^{2}}=1$

โดยการย้ายตำแหน่งและหมุนรูปผิวกำลังสองทุกรูป สามารถแปลงให้อยู่ในรูปบรรทัดฐานได้ ในปริภูมิแบบยุคลิดสามมิติ ผิวกำลังสองนี้จะมีรูปบรรทัดฐาน 16 รูป โดยมีรูปแบบที่น่าสนใจดังต่อไปนี้:

ทรงรี	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1\,$
ทรงคล้ายทรงกลม (กรณีพิเศษของ ทรงรี)	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{a^{2}}}+{\frac {z^{2}}{b^{2}}}=1\,$
ทรงกลม (กรณีพิเศษของทรงคล้างทรงกลม)	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{a^{2}}}+{\frac {z^{2}}{a^{2}}}=1\,$
ทรงพาราโบลาเชิงวงรี	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-z=0\,$
ทรงพาราโบลาเชิงวงกลม	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{a^{2}}}-z=0\,$
ทรงพาราโบลาเชิงไฮเพอร์โบลา	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}-z=0\,$
ทรงไฮเพอร์โบลาชิ้นเดี่ยว	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1\,$
ทรงไฮเพอร์โบลาสองชิ้น	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1\,$
ทรงกรวย	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=0\,$
ทรงกระบอกเชิงวงรี	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\,$
ทรงกระบอกเชิงวงกลม	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{a^{2}}}=1\,$
ทรงกระบอกเชิงไฮเพอร์โบลา	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1\,$
ทรงกระบอกเชิงไฮพาราโบลา	$x^{2}+2y=0\,$

ภาคขยายของผิวกำลังสอง

นอกเหนือจากรูปแบบผิวกำลังสองมาตรฐานที่ได้กล่าวถึงไปแล้ว ยังมีการดัดแปลงรูปแบบของสมการพื้นผิวดังกล่าวเพื่อใช้ในการแทนรูปทรงเรขาคณิตที่ซับซ้อนขึ้น เช่น ซุปเปอร์ควอดริก และไฮเปอร์ควอดริก

ซุปเปอร์ควอดริก

สมการบรรทัดฐานของซุปเปอร์ควอดริกที่มีจุดศูนย์กลางที่ (0,0,0) คือ

$\left({x^{2} \over a^{2}}\right)^{1 \over \epsilon _{1}}+\left({y^{2} \over b^{2}}\right)^{1 \over \epsilon _{2}}+\left({z^{2} \over c^{2}}\right)^{1 \over \epsilon _{3}}=1$

หรือ ในรูป

$\,x(\theta ,\phi )=\,$	$a\,\operatorname {sign} (\cos \theta \cos \phi )\,|\cos \theta \cos \phi |^{\epsilon _{1}})$
$\,y(\theta ,\phi )=\,$	$b\,\operatorname {sign} (\sin \theta \cos \phi )\,|\sin \theta \cos \phi |^{\epsilon _{2}})$
$\,z(\theta ,\phi )=\,$	$c\,\operatorname {sign} (\sin \phi )\,|\sin \phi |^{\epsilon _{3}})$

โดย ${-\pi \over 2}\leq \phi \leq {\pi \over 2}$ และ $-\pi \leq \theta <\pi$

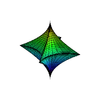
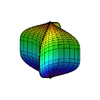
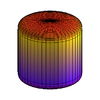
สิ่งที่ซุปเปอร์ควอดริกแตกต่างไปจากผิวกำลังสองคือ เลขยกกำลัง $\,\epsilon _{1},\ \epsilon _{2},\ \epsilon _{3}\,$ โดยที่ค่า $\,\epsilon _{1}\,$ และ $\,\epsilon _{2}\,$ นั้นมีผลต่อรูปร่างในแนวนอน ส่วน $\,\epsilon _{3}\,$ นั้นผลต่อรูปร่างในแนวตั้ง ดังแสดงในรูปด้านล่าง

$\,\epsilon _{3}=4\,$
$\,\epsilon _{3}=2\,$
$\,\epsilon _{3}=1\,$
$\,\epsilon _{3}=0.5\,$
$\,\epsilon _{3}=0.1\,$
$\,\epsilon _{3}=0\,$
$\,\epsilon _{1}=\epsilon _{2}=0\,$	$\,\epsilon _{1}=\epsilon _{2}=0.5\,$	$\,\epsilon _{1}=\epsilon _{2}=1\,$	$\,\epsilon _{1}=\epsilon _{2}=2\,$	$\,\epsilon _{1}=\epsilon _{2}=4\,$

ไฮเปอร์ควอดริก

ไฮเปอร์ควอดริกเป็นส่วนที่ขยายต่อจากซุปเปอร์ควอดริกให้มีความสามารถในการจำลองผิวที่ซับซ้อนยิ่งขึ้น โดยซุปเปอร์ควอดริกนั้นเป็นเพียงกรณีพิเศษของไฮเปอร์ควอดริก ไฮเปอร์ควอดริกนั้นสามารถเขียนในรูปสมการทางคณิตศาสตร์ดังต่อไปนี้

$\sum _{i=1}^{N}{|l_{i}(x,y,z)|^{1 \over \epsilon _{i}}}=1$

โดย

$\,l_{i}(x,y,z)=a_{i}x+b_{i}y+c_{i}z+d_{i}\,$

และ $\,N\geq 3\,$

$\,\epsilon _{1}=\epsilon _{2}=\epsilon _{3}=1\,$	$\,\epsilon _{1}=\epsilon _{2}=\epsilon _{3}=2\,$	$\,\epsilon _{1}=\epsilon _{3}=2,\epsilon _{2}=0.2\,$

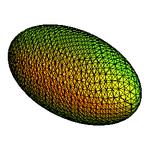
นอกเหนือจากรูปแบบของไฮเปอร์ควอดริกข้างต้น แล้วก็ยังมีการพัฒนาเพิ่มเติมความซับซ้อนของรูปร่างไฮเปอร์ควอดริก เรียกว่า "คอมโพสิทไฮเปอร์ควอดริก" หรือ "ไฮบริดไฮเปอร์ควอดริก" โดยส่วนที่เพิ่มอาจอยู่ในรูปพหุนามของเลขชี้กำลัง

$\sum _{i=1}^{N_{p}}{|l_{i}^{(pol)}(x,y,z)|^{1 \over \epsilon _{i}}}+\sum _{m=1}^{M}{w_{m}\cdot e^{-\sum _{j=1}^{N_{e}}{|l_{mj}^{(exp)}(x,y,z)|^{1 \over \epsilon _{mj}}}}}=1$

พจน์ที่เพิ่มเข้ามา มีผลในการปรับแต่งรูปทรงของผิวเฉพาะที่ เช่นใช้ในการเพิ่มหลุมหรือรอยบุ๋ม ดังแสดงในภาพด้านล่าง

	$\Rightarrow$
ไฮเปอร์ควอดริก		ภาพคอมโพสิทไฮเปอร์ควอดริก โดยการเพิ่มพจน์ของเลขยกกำลัง 1 พจน์