ควาร์ก

โปรตอน อนุภาคมูลฐานของอะตอมประกอบไปด้วยอัพควาร์กสองตัว (สีน้ำเงินและแดง) กับดาวน์ควาร์กอีกหนึ่งตัว (สีเขียว)

ควาร์ก (อังกฤษ: quark อ่านว่า /kwɔrk/ หรือ /kwɑrk/) คืออนุภาคที่มีขนาดเล็กกว่าอะตอม ตัวอย่างคือเมื่อมีสิ่งๆ หนึ่งล่วงล้ำเข้าสู่อาณาเขตของหลุมดำ หากมันมีความเร็วน้อยกว่าหรือเท่ากับแสง มันจะถูกดูดและบดขยี้ทันที โดยจะถูกบดจนกลายเป็นอะตอม และถูกบดอีกจนกลายเป็นควาร์ก และไม่สามารถแยกย่อยได้อีก ถือเป็นอนุภาคที่มีขนาดเล็กที่สุดในจักรวาล นี่เป็นตัวอย่างหนึ่งของความเข้าใจของนักวิทยาศาสตร์ซึ่งได้รับการพิสูจน์แล้ว และอาจเป็นบันไดสู่เทคโนโลยีในอนาคต

ควาร์กมีอยู่ 6 ชนิด เรียกว่า 6 เฟลเวอร์ (flavor) ได้แก่ อัพ (up), ดาวน์ (down), ชาร์ม (charm), สเตรนจ์ (strange), ท็อป (top), และ บ็อทท็อม (bottom) ควาร์กแบบอัพและดาวน์เป็นแบบที่มีมวลต่ำที่สุดในบรรดาควาร์กทั้งหมด ควาร์กที่หนักกว่าจะเปลี่ยนแปลงมาเป็นควาร์กแบบอัพและดาวน์อย่างรวดเร็วโดยผ่านกระบวนการการเสื่อมสลายของอนุภาค (particle decay) ซึ่งเป็นกระบวนการที่เปลี่ยนสถานะมวลมากกว่ามาเป็นสถานะมวลต่ำกว่า ด้วยเหตุนี้ ควาร์กแบบอัพและดาวน์จึงเป็นชนิดที่เสถียร และพบได้ทั่วไปมากที่สุดในเอกภพ ขณะที่ควาร์กแบบชาร์ม สเตรนจ์ ท็อป และบ็อทท็อม จะเกิดขึ้นได้ก็จากการชนที่มีพลังงานสูงเท่านั้น (เช่นที่อยู่ในรังสีคอสมิกและในเครื่องเร่งอนุภาค)

ควาร์กมีคุณสมบัติในตัวหลายประการ ซึ่งรวมถึงประจุไฟฟ้า ประจุสี สปิน และมวล ควาร์กเป็นอนุภาคมูลฐานเพียงชนิดเดียวในแบบจำลองมาตรฐานของฟิสิกส์อนุภาคที่สามารถมีปฏิกิริยากับแรงพื้นฐานได้ครบหมดทั้ง 4 ชนิด (คือ แรงแม่เหล็กไฟฟ้า, แรงโน้มถ่วง, อันตรกิริยาอย่างเข้ม และอันตรกิริยาอย่างอ่อน) รวมถึงยังเป็นอนุภาคเพียงชนิดเดียวเท่าที่รู้จักซึ่งประจุไฟฟ้าไม่ใช่เลขจำนวนเต็มคูณกับประจุมูลฐาน ทุกๆ เฟลเวอร์ของควาร์กจะมีคู่ปฏิอนุภาค เรียกชื่อว่า แอนติควาร์ก ซึ่งมีความแตกต่างกับควาร์กแค่เพียงคุณสมบัติบางส่วนที่มีค่าทางขนาดเท่ากันแต่มีสัญลักษณ์ตรงกันข้าม

มีการนำเสนอแบบจำลองควาร์กจากนักฟิสิกส์ 2 คนโดยแยกกัน คือ เมอร์เรย์ เกลล์-แมนน์ และ จอร์จ ซวิก ในปี ค.ศ. 1964 ซึ่งเสนอว่าควาร์กเป็นส่วนหนึ่งของรูปแบบของฮาดรอน มีหลักฐานที่แสดงถึงการมีอยู่จริงของพวกมันเพียงเล็กน้อยเท่านั้น จนกระทั่งมีการทดลองการชนแบบไม่ยืดหยุ่น (Deep inelastic scattering) ที่ห้องทดลองการเร่งอนุภาคแห่งชาติ SLAC (SLAC National Accelerator Laboratory) ในปี ค.ศ. 1968 เริ่มมีการสังเกตเฟลเวอร์ทั้งหกของควาร์กจากการทดลองเร่งอนุภาคในครั้งนั้น ควาร์กแบบท็อป ซึ่งสังเกตพบครั้งแรกที่ เฟอร์มิแล็บ ในปี ค.ศ. 1995 นับเป็นเฟลเวอร์ที่ถูกค้นพบเป็นลำดับสุดท้าย

การจัดประเภท

ดูเพิ่มที่ แบบจำลองมาตรฐาน

อนุภาค 6 ชนิดในแบบจำลองมาตรฐานเป็นควาร์ก (แสดงด้วยสีม่วง) สามคอลัมน์แรกของตารางเรียกว่าเป็น เจเนเรชั่น ของสสาร

แบบจำลองมาตรฐานเป็นกรอบการทำงานในทางทฤษฎีใช้เพื่ออธิบายถึงอนุภาคมูลฐานทั้งหมดที่รู้จักกันในปัจจุบัน ซึ่งรวมถึงอนุภาคที่ยังไม่อาจสังเกตพบ คือ อนุภาคฮิกส์ ด้วย แบบจำลองนี้มีควาร์กทั้ง 6 เฟลเวอร์ ชื่อว่า อัพ (u), ดาวน์ (d), ชาร์ม (c), สเตรนจ์ (s), ท็อป (t), และบ็อทท็อม (b) ปฏิอนุภาคของควาร์กเรียกว่า แอนติควาร์ก แสดงด้วยสัญลักษณ์ขีดบนอยู่เหนือตัวอักษรของควาร์ก เช่น u แสดงถึงแอนติควาร์กของอัพ แอนติควาร์กมีลักษณะเหมือนกับปฏิสสารโดยทั่วไป คือมีมวลที่เท่ากัน ช่วงชีวิตเฉลี่ยเท่ากัน และมีสปินเหมือนกันกับควาร์กคู่ของมัน แต่มีประจุไฟฟ้ากับประจุอื่นๆ ในสัญลักษณ์ที่ตรงกันข้าม

ควาร์กเป็นอนุภาคที่มีสปิน spin-1/2 หมายความว่า มันเป็นเฟอร์มิออนตามทฤษฎีบทสปินเชิงสถิติ (spin-statistics theorem) มีลักษณะตามหลักการกีดกันของเพาลีซึ่งระบุว่า ไม่มีเฟอร์มิออนที่เหมือนกันสองตัวใดๆ จะสามารถมีสถานะควอนตัมเดียวกันได้ ซึ่งตรงกันข้ามกับโบซอน (อนุภาคที่มีสปินเป็นเลขจำนวนเต็ม) ที่สามารถมีหลายตัวอยู่ในสถานะเดียวกันได้ ส่วนที่แตกต่างจากเลปตอน คือ ควาร์กมีประจุสี อันเป็นเหตุให้มันสามารถเข้าร่วมในอันตรกิริยาอย่างเข้มได้ ผลจากความดึงดูดระหว่างควาร์กที่แตกต่างกันสองตัว ทำให้เกิดการรวมตัวกันเป็นอนุภาคประกอบที่รู้จักกันในชื่อ ฮาดรอน (ดูหัวข้อ "อันตรกิริยาอย่างเข้มกับประจุสี" ด้านล่าง)

คุณสมบัติ

ประจุไฟฟ้า

ดูเพิ่มที่ ประจุไฟฟ้า

ควาร์กมีค่าประจุไฟฟ้าเป็นเศษส่วน คือ −1/3 or +2/3 ของขนาดประจุมูลฐานขึ้นกับว่าเป็นเฟลเวอร์อะไร ถ้าเป็นควาร์กแบบอัพ ชาร์ม และท็อป (รวมๆ กันมักเรียกว่า "ควาร์กประเภทอัพ") จะมีประจุ +2/3 ขณะที่ควาร์กแบบดาวน์ สเตรนจ์ และบ็อททอม ("ควาร์กประเภทดาวน์") จะมีประจุ −1/3 แอนติควาร์กจะมีประจุตรงกันข้ามกับควาร์กที่เป็นคู่ของมัน คือ แอนติควาร์กประเภทอัพมีประจุ −2/3 และแอนติควาร์กประเภทดาวน์มีประจุ +1/3 ในเมื่อประจุไฟฟ้าของฮาดรอนนั้นเป็นผลรวมของประจุของควาร์กทั้งหมดที่เป็นส่วนประกอบ ดังนั้นฮาดรอนทั้งหมดจึงมีประจุเป็นจำนวนเต็ม ส่วนประสมของควาร์ก 3 ตัว (แบริออน), แอนติควาร์ก 3 ตัว (แอนติแบริออน) หรือควาร์กและแอนติควาร์ก 1 ตัว (มีซอน) ก็มีค่าประจุเป็นจำนวนเต็มเสมอ ยกตัวอย่างเช่น ส่วนประกอบนิวเคลียสอะตอมของฮาดรอนประกอบด้วยนิวตรอนและโปรตอน มีประจุ 0 และ +1 ตามลำดับ โดยที่นิวตรอนประกอบด้วยดาวน์ควาร์ก 2 ตัวและอัพควาร์ก 1 ตัว ส่วนโปรตอนประกอบด้วยอัพควาร์ก 2 ตัวและดาว์นควาร์ก 1 ตัว

สปิน

ดูเพิ่มที่ สปิน (ฟิสิกส์)

สปิน คือคุณสมบัติภายในของอนุภาคพื้นฐาน ทิศทางของสปินเป็นองศาอิสระที่มีความสำคัญ ในบางครั้งอาจมองภาพเป็นการหมุนของวัตถุรอบแกนของมันเองก็ได้ (ซึ่งเป็นที่มาของคำว่า สปิน ที่หมายถึง การปั่น) แม้จะเป็นการชี้นำที่ผิดไปบ้างในระดับของซับอะตอมมิกเนื่องจากเชื่อกันว่าอนุภาคพื้นฐานนั้นมีลักษณะเป็นจุด

เราสามารถแสดงสปินได้ด้วยเวกเตอร์ซึ่งมีความยาววัดได้ในหน่วยของค่าคงที่ของพลังค์แบบย่อ ħ (อ่านว่า "เอชบาร์") สำหรับควาร์กนั้น การวัดองค์ประกอบเวกเตอร์ของสปินในแกนใดๆ จะได้ค่าออกมาเป็น +ħ/2 หรือ −ħ/2 อย่างใดอย่างหนึ่ง ด้วยเหตุนี้ ควาร์กจึงจัดว่าเป็นอนุภาค spin-1/2 องค์ประกอบของสปินตามแกนที่กำหนด (เรียกว่าแกน z) มักย่อด้วยรูปลูกศรชี้ขึ้น ↑ สำหรับค่า +1/2 และลูกศรชี้ลง ↓ สำหรับค่า −1/2 โดยวางไว้ที่ด้านหลังสัญลักษณ์ของเฟลเวอร์ ตัวอย่างเช่น อัพควาร์กที่มีสปิน +1/2 ตามแกน z จะเขียนย่อว่า u↑.

อันตรกิริยาอย่างอ่อน

ดูบทความหลักที่ อันตรกิริยาอย่างอ่อน

ไดอะแกรมของเฟย์นแมนของการสลายให้อนุภาคบีตาโดยที่แกนเวลาชี้ขึ้นด้านบน ซึ่ง CKM matrix (ดูคำอธิบายข้างล่าง) เป็นตัวเข้ารหัสความน่าจะเป็นของเหตุการณ์นี้ รวมถึงการสลายตัวของควาร์กแบบอื่นๆ

ควาร์กที่มีเฟลเวอร์แบบหนึ่งสามารถเปลี่ยนรูปไปเป็นควาร์กของเฟลเวอร์อีกแบบหนึ่งได้ก็โดยผ่านอันตรกิริยาอย่างอ่อน ซึ่งเป็นอันตรกิริยาพื้นฐานชนิดหนึ่งในจำนวนสี่ชนิดของฟิสิกส์อนุภาค ทั้งนี้โดยการดูดซับหรือแผ่ W boson ทำให้ควาร์กประเภทอัพ (อัพ ชาร์ม และท็อปควาร์ก) สามารถเปลี่ยนไปเป็นควาร์กประเภทดาวน์ (ดาวน์ สเตรนจ์ และบ็อทท็อม) ได้ ในทางกลับกันก็เช่นเดียวกัน กลไกการเปลี่ยนรูปของเฟลเวอร์นี้ทำให้เกิดกระบวนการแผ่รังสีที่ทำให้เกิดการสลายให้อนุภาคบีตา ซึ่งนิวตรอน (n) 1 ตัวจะแบ่งตัวกลายเป็นโปรตอน (p) 1 ตัว อิเล็กตรอน (e⁻) 1 ตัว และอิเล็กตรอนแอนตินิวตริโน (νe) 1 ตัว (ดูภาพประกอบ) สิ่งนี้จะเกิดขึ้นเมื่อดาวน์ควาร์กตัวหนึ่งในนิวตรอน (udd) เสื่อมสลายลงเป็นอัพควาร์กโดยการแผ่อนุภาคเสมือนของ W⁻ โบซอน เปลี่ยนให้นิวตรอนกลายไปเป็นโปรตอน (uud) จากนั้นโบซอน W⁻ นี้จะเสื่อมสลายไปเป็นอิเล็กตรอน 1 ตัวกับอิเล็กตรอนแอนตินิวตริโน 1 ตัว

n	→	p	+	e−	+	νe	(Beta decay, hadron notation)
udd	→	uud	+	e−	+	νe	(Beta decay, quark notation)

การสลายให้อนุภาคบีตาทั้ง 2 แบบนี้ รวมถึงการกระบวนการย้อนกลับ มักมีการใช้อย่างสม่ำเสมอในทางการแพทย์ เช่น การตรวจเอกซ์เรย์ด้วยโพสิตรอน (PET) และในการทดลองฟิสิกส์พลังงานสูง เช่น การตรวจจับนิวตริโน

ภาพแสดงแรงของอันตรกิริยาอย่างอ่อนระหว่างควาร์กทั้งหก "ความเข้ม" ของเส้นถูกนิยามขขึ้นโดยองค์ประกอบของ CKM matrix

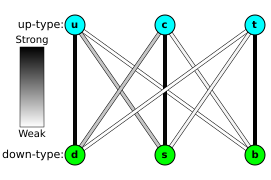
ขณะที่กระบวนการเปลี่ยนรูปเฟลเวอร์นี้เกิดขึ้นเหมือนๆ กันในควาร์กทุกชนิด ควาร์กแต่ละตัวก็มีแนวโน้มจะเปลี่ยนรูปไปเป็นควาร์กในตระกูลเดียวกันกับตัวเอง แนวโน้มความสัมพันธ์ในการเปลี่ยนรูปของเฟลเวอร์เหล่านี้เขียนได้ในรูปแบบตารางเมทริกซ์ เรียกว่า Cabibbo–Kobayashi–Maskawa matrix (CKM matrix) ค่าโดยประมาณของค่าต่างๆ ใน CKM matrix เป็นดังนี้:

$|V_ud| ≅ 0.974; |V_us| ≅ 0.225; |V_ub| ≅ 0.003; |V_cd| ≅ 0.225; |V_cs| ≅ 0.973; |V_cb| ≅ 0.041; |V_td| ≅ 0.009; |V_ts| ≅ 0.040; |V_tb| ≅ 0.999.$

โดยที่ V_ij แทนแนวโน้มของควาร์กที่มีเฟลเวอร์ i ที่จะเปลี่ยนไปเป็นควาร์กแบบเฟลเวอร์ j (หรือในทางกลับกัน)

มีตารางเมทริกซ์อันตรกิริยาอย่างอ่อนที่เทียบเท่ากันนี้สำหรับเลปตอน (อยู่ทางขวาของ W boson ในไดอะแกรมการสลายอนุภาคบีตาที่แสดงไว้ข้างบน) เรียกว่า Pontecorvo–Maki–Nakagawa–Sakata matrix (PMNS matrix) ทั้งเมทริกซ์ CKM และ PMNS ล้วนอธิบายถึงการเปลี่ยนรูปของเฟลเวอร์ แต่ความเชื่อมโยงระหว่างเมทริกซ์ทั้งสองนี้ยังไม่เป็นที่เข้าใจชัดเจน

หนังสืออ่านเพิ่ม

• D.J. Griffiths (2008). Introduction to Elementary Particles (2nd ed.). Wiley–VCH. ISBN 3527406018. 
• I.S. Hughes (1985). Elementary particles (2nd ed.). Cambridge University Press. ISBN 0-521-26092-2. 
• R. Oerter (2005). The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics. Pi Press. ISBN 0132366789. 
• A. Pickering (1984). Constructing Quarks: A Sociological History of Particle Physics. The University of Chicago Press. ISBN 0-226-66799-5. 
• B. Povh (1995). Particles and Nuclei: An Introduction to the Physical Concepts. Springer–Verlag. ISBN 0-387-59439-6. 
• M. Riordan (1987). The Hunting of the Quark: A true story of modern physics. Simon & Schuster. ISBN 0-671-64884-5. 
• B.A. Schumm (2004). Deep Down Things: The Breathtaking Beauty of Particle Physics. Johns Hopkins University Press. ISBN 0-8018-7971-X. 

แหล่งข้อมูลอื่น

• 1969 Physics Nobel Prize lecture by Murray Gell-Mann
• 1976 Physics Nobel Prize lecture by Burton Richter
• 1976 Physics Nobel Prize lecture by Samuel C.C. Ting
• 2008 Physics Nobel Prize lecture by Makoto Kobayashi
• 2008 Physics Nobel Prize lecture by Toshihide Maskawa
• The Top Quark And The Higgs Particle by T.A. Heppenheimer – A description of CERN's experiment to count the families of quarks.