ไซคลอยด์
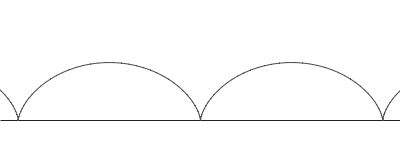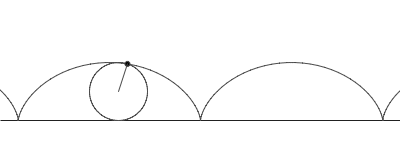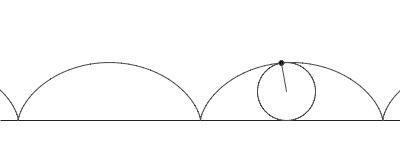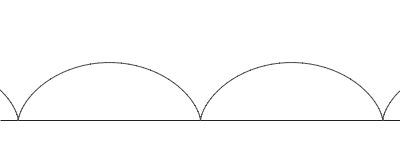
ไซคลอยด์ (อังกฤษ: cycloid) คือเส้นโค้งชนิดหนึ่ง นิยามจากรอยเคลื่อนที่ของจุดจุดหนึ่งบนเส้นรอบรูปวงกลม (ล้อกลม) ซึ่งรูปวงกลมนั้นกลิ้งไปตามเส้นตรง ทำให้เกิดเส้นโค้งนูนเป็นลอนเป็นราย
ไซคลอยด์เป็นตัวอย่างหนึ่งของรูเลตต์ (roulette) ซึ่งเกิดจากกลิ้งล้อกลมบนเส้นโค้งอื่น และเป็นกรณีหนึ่งของโทรคอยด์ (trochoid) ซึ่งจุดไม่จำเป็นต้องอยู่บนเส้นรอบรูปวงกลม
สมการ
[แก้]
ไซคลอยด์ที่ลากผ่านจุดกำเนิด ซึ่งสร้างขึ้นโดยรูปวงกลมรัศมี r ที่กลิ้งบนแกน x มีสมการอิงตัวแปรเสริมดังนี้
เมื่อ t เป็นจำนวนจริง คือมุมในหน่วยเรเดียนที่รูปวงกลมกลิ้งไป (บางครั้งอาจใช้ θ แทน t)
เส้นโค้งชนิดนี้สามารถหาอนุพันธ์ได้ทุกตำแหน่งยกเว้น บัพแหลม (cusp) คือจุดที่สัมผัสกับแกน x ซึ่งอนุพันธ์จะกลายเป็น ∞ หรือ −∞ เมื่อเข้าใกล้จุดบัพแหลม ซึ่งตรงตามสมการเชิงอนุพันธ์สามัญดังนี้
พื้นที่ใต้กราฟ
[แก้]เนื่องจากไซคลอยด์หนึ่งรอบ ที่สร้างโดยรูปวงกลมรัศมี r จากสมการอิงตัวแปรเสริมด้านบน จะได้ค่าของตัวแปรเสริม t ที่มีค่าอยู่ในช่วง [0, 2π]
และเนื่องจาก
เราสามารถคำนวณหาพื้นที่ใต้กราฟของไซคลอยด์หนึ่งรอบโดยการหาปริพันธ์ดังนี้
นั่นคือเท่ากับสามเท่าของพื้นที่ของรูปวงกลม
ความยาวเส้นโค้ง
[แก้]ความยาวของเส้นโค้งไซคลอยด์หนึ่งรอบ สามารถหาได้จากความยาวของส่วนย่อยๆ บนเส้นโค้ง ซึ่ง t มีค่าในช่วง [0, 2π]
นั่นคือเท่ากับแปดเท่าของรัศมีของรูปวงกลม
ดูเพิ่ม
[แก้]- เอพิไซคลอยด์ (epicycloid)
- ไฮโพไซคลอยด์ (hypocycloid)
- โทรคอยด์ (trochoid)
- เอพิโทรคอยด์ (epitrochoid)
- ไฮโพโทรคอยด์ (hypotrochoid)






