ทรงลูกบาศก์
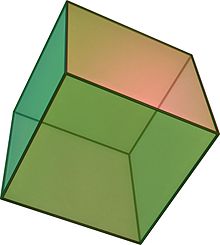
ทรงลูกบาศก์ (อังกฤษ: cube) เป็นทรงหลายหน้า (polyhedron) ที่ประกอบด้วยหน้ารูปสี่เหลี่ยมจัตุรัสทั้ง 6 หน้า โดยแต่ละจุดยอด (vertex) จะล้อมรอบด้วยหน้ารูปสี่เหลี่ยมเป็นจำนวน 3 หน้าทุกจุด ทรงนี้มี 8 จุดยอดมุม 12 ขอบ และเป็นหนึ่งในทรงตันเพลโต (Platonic solid) ทรงลูกบาศก์เป็นทรงหลายหน้าที่คู่กันกับทรงแปดหน้า มีสมมาตรแบบทรงลูกบาศก์ (หรือเรียกว่าสมมาตรแบบทรงแปดหน้า Oh) ทรงลูกบาศก์คือรูปทรงไฮเพอร์คิวบ์ (hypercube) ที่อยู่บนสามมิติ
ทรงลูกบาศก์สามารถเรียกได้ในชื่ออื่น ๆ เช่น ทรงสี่เหลี่ยมจัตุรัส, ปริซึมสี่เหลี่ยมจัตุรัส, ทรงหกหน้าปรกติ (regular hexahedron), เทรปโซฮีดรอนสามเหลี่ยม (trigonal trapezohedron) เป็นต้น
พิกัดคาร์ทีเซียน[แก้]
สำหรับทรงลูกบาศก์ที่มีจุดศูนย์กลางอยู่ที่จุดกำเนิด โดยขอบทั้งหมดขนานกับแกนและมีความยาวด้านละ 2 หน่วย พิกัดคาร์ทีเซียนของจุดยอดทั้งหมดคือ
- (±1, ±1, ±1)
ซึ่งเนื้อในของทรงลูกบาศก์ประกอบด้วยจุดทุกจุด (x0, x1, x2) ที่ −1 < xi < 1
สูตรคำนวณ[แก้]
สำหรับทรงลูกบาศก์ที่มีด้านยาวด้านละ a หน่วย
| พื้นที่ผิว (A) | |
| ปริมาตร (V) | |
| รัศมีของทรงกลมภายนอก | |
| รัศมีของทรงกลมที่สัมผัสกับขอบ | |
| รัศมีของทรงกลมภายใน |
และเนื่องจากปริมาตรของทรงลูกบาศก์มีค่าเท่ากับกำลังสามของด้านหนึ่งด้าน a×a×a ดังนั้นค่ากำลังสามของจำนวนใด ๆ จึงถูกเรียกอีกชื่อหนึ่งว่า cube ในภาษาอังกฤษ ทำนองเดียวกับ square ที่ใช้เรียกแทนกำลังสอง
ทรงลูกบาศก์เป็นทรงสี่เหลี่ยมมุมฉากที่มีปริมาตรมากที่สุด เมื่อเทียบกับทรงสี่เหลี่ยมมุมฉากอื่น ๆ ที่มีพื้นที่ผิวเท่ากัน หรือเมื่อมีความยาวของด้านรวมทั้งหมดเท่ากัน (กว้าง+ยาว+สูง)
ดูเพิ่ม[แก้]
- ลูกเต๋า
- ทรงสี่เหลี่ยมมุมฉาก (cuboid)
- ทรงสี่เหลี่ยมขนมเปียกปูน (rhombohedron)





