เศรษฐมิติ

เศรษฐมิติ (อังกฤษ: econometrics) เป็นการประยุกต์วิธีทางสถิติเพื่อวิเคราะห์ความสัมพันธ์ทางเศรษฐศาสตร์ด้วยหลักฐานเชิงประจักษ์ วิธีทางเศรษฐมิติถูกใช้เพื่อการทดสอบทฤษฎีเศรษฐศาสตร์ การพยากรณ์ทางเศรษฐกิจ ไปจนถึงการประเมินผลนโยบายต่างๆ^[1] เครื่องมือพื้นฐานของเศรษฐมิติที่ใช้กันทั่วไปมีพื้นฐานมาจากการวิเคราะห์การถดถอย โดยเฉพาะแบบจำลองการถดถอยเชิงเส้น^[2] ทฤษฎีเศรษฐมิติใช้ทฤษฎีสถิติศาสตร์และคณิตสถิติศาสตร์เพื่อประเมินและพัฒนาระเบียบวิธีทางเศรษฐมิติ นักเศรษฐมิติทดลองที่จะหาตัวประมาณค่าใหม่ๆ ที่มีคุณสมบัติทางสถิติที่เหมาะสม ซึ่งประกอบไปด้วย ความไม่เบี่ยงเบน ประสิทธิภาพ และความต้องกัน เศรษฐมิติประยุกต์ ใช้เศรษฐมิติเชิงทฤษฎีและข้อมูลในโลกความเป็นจริงในการประเมินทฤษฎีเศรษฐศาสตร์ สร้างแบบจำลองทางเศรษฐมิติ วิเคราะห์ประวัติศาสตร์เศรษฐกิจ และการพยากรณ์

การจัดวิชาเศรษฐมิติเป็นสาขาวิชาในตัวเองและเรียกชื่อในภาษาอังกฤษว่า econometrics มีที่มาจากรากนาร์ ฟริสช์^[1] ซึ่งเป็นผู้ร่วมก่อตั้งสมาคมเศรษฐมิติและเป็นบรรณาธิการคนแรกของวารสารอิโคโนเมทริคา

แบบจำลองพื้นฐาน: การถดถอยเชิงเส้น

เครื่องมือพื้นฐานของเศรษฐมิติคือแบบจำลองถดถอยเชิงเส้นหลายตัวแปร ในเศรษฐมิติสมัยใหม่ เครื่องมือทางสถิติอื่น ๆ มักถูกใช้อยู่บ่อยครั้ง แต่การถดถอยเชิงเส้นก็ยังถูกใช้เป็นจุดเริ่มของการวิเคราะห์อยู่เป็นประจำ^[3] การถดถอยเชิงเส้นเป็นวิธีประมาณค่าพารามิเตอร์ในแบบจำลอง การประมาณการถดถอยเชิงเส้นของตัวแปรสองตัวแปรสามารถแสดงได้ด้วยภาพเป็นเส้นที่ลากผ่านข้อมูล

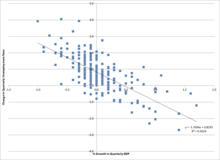
ตัวอย่าง กฎของโอคุน (Okun's law) ซึ่งเป็นความสัมพันธ์ระหว่างการเติบโตของ GDP และอัตราการว่างงาน ความสัมพันธ์นี้ถูกแทนที่ได้ด้วยการถดถอยเชิงเส้นซึ่งการเปลี่ยนแปลงของอัตราการว่างงาน ( $\Delta \ {\text{Unemployment}}$ ) เป็นฟังก์ชันของจุดตัดแกนตั้ง ( $\beta _{0}$ ) ค่าของอัตราการเติบโตของ GDP (Growth) คูณด้วยค่าสหสัมพันธ์ความชัน $\beta _{1}$ และค่าความคลาดเคลื่อน $\varepsilon$ ดังนี้

$\Delta \ {\text{Unemployment}}$ = $\beta _{0}$ + $\beta _{1}\ {\text{Growth}}$ + $\varepsilon$

ค่าพารามิเตอร์ $\beta _{0}$ and $\beta _{1}$ สามารถถูกประมาณการขึ้นได้ด้วยวิธีถดถอยเชิงเส้น สมมติว่า $\beta _{1}$ ถูกประมาณค่าเท่ากับ −1.77 และ $\beta _{0}$ ถูกประมาณค่าเท่ากับ 0.83 หมายความว่าถ้าอัตราการเติบโตของ GDP เพิ่มขึ้นร้อยละ 1 อัตราการว่างงานคาดว่าจะลดลงร้อยละ 1.77 แบบจำลองนี้สามารถถูกทดสอบนัยสำคัญทางสถิติว่าการลดลงของอัตราการว่างงานมีความเกี่ยวพันธ์กับการเพิ่มของอัตราการเติบโตของ GDP หรือไม่ ได้ด้วยการทดสอบสมมติฐาน ถ้าค่าประมาณของ $\beta _{1}$ ไม่มีความแตกต่างอย่างมีนัยสำคัญจาก 0 แล้ว จะถือว่าไม่มีหลักฐานที่รับรองว่าการเปลี่ยนแปลงของอัตราการเติบโตของ GDP และอัตราการว่างงานมีความสัมพันธ์กัน

ทฤษฎีทางเศรษฐมิติ

ทฤษฎีทางเศรษฐมิติจะใช้ทฤษฎีสถิติมาการประเมินและพัฒนาวิธีการทางเศรษฐมิติ นักเศรษฐมิติจะพยายามหาตัวประมาณการ (estimator) ที่มีคุณสมบัติทางสถิติที่ต้องการประกอบด้วยความไม่เอนเอียง (unbiasedness) ประสิทธิภาพ (efficiency) และความคงเส้นคงวา (consistency) ตัวประมาณการจะไม่เอนเอียงก็ต่อเมื่อค่าคาดหวังของพารามิเตอร์มีค่าเท่าค่าจริงของพารามิเตอร์ ตัวประมาณการจะมีประสิทธิภาพก็ต่อเมื่อตัวประมาณการมีค่าความคลาดเคลื่อนมาตรฐานน้อยกว่าตัวประมาณการที่ไม่เอนเอียงอื่นๆ ที่มีขนาดตัวอย่างเท่ากัน และตัวประมาณการจะมีความคงเส้นคงวาก็ต่อเมื่อตัวมาณการมีค่าเข้าหาค่าจริงของพารามิเตอร์มากขึ้นเมื่อขนาดตัวอย่างเพิ่มขึ้นกับ วิธีกำลังสองน้อยที่สุด หรือ Ordinary least squares (OLS) เป็นวิธีประมาณการที่มักจะถูกใช้อยู่บ่อยครั้งเนื่องจากให้ความเป็นตัวประมาณการที่ไม่เอนเอียงเชิงเส้นที่ดีที่สุด best linear unbiased estimator หรือ BLUE ภายใต้สมมติฐาน Gauss-Markov assumptions เมื่อสมมติฐานเหล่านี้ถูกละเมิดหรือมีความต้องการคุณสมบัติเชิงสถิติอื่นๆ เทคนิคการประมาณค่าอื่น เช่น การประมาณด้วยวิธีความน่าจะเป็นสูงสุด วิธีการเชิงโมเมนต์ทั่วไป หรือวิธีการกำลังสองน้อยที่สุดแบบทั้วไป จะถูกนำมาใช้ ตัวประมาณค่าที่ใช้ความเชื่อก่อนหน้าได้รับการสนับสนุนจากผู้ที่ชอบในสถิติแบบเบย์ มากกว่าการใช้วิธีแบบดั้งเดิม หรือวิธีการเชิงความถี่

วิธีทางเศรษฐมิติ

เศรษฐมิติประยุกต์ จะใช้ทฤษฎีทางสถิติและข้อมูลจริงในการประเมินทฤษฎีทางเศรษฐศาสตร์ พัฒนาแบบจำลองทางเศรษฐศาสตร์ วิเคราะห์ประวัติศาสตร์ของเศรษฐกิจ และใช้ในการพยากรณ์^[4]

เศรษฐมิติอาจะใช้แบบจำลองทางสถิติในการตอบปัญหาทางเศรษฐศาสตร์ แต่โดยส่วนใหญ่มักจะใช้ข้อมูลที่ได้จากการสังเกตมากกว่าข้อมูลจากการทดลอง^[5] การออกแบบการศึกษาในสาขาเศรษฐมิติจะเหมือนกับการออกแบบการศึกษาในสาขาที่ต้องใช้ข้อมูลที่ได้จากการสังเกตอื่นๆ ได้แก่ ดาราศาสตร์ วิทยาการระบาด สังคมวิทยา และรัฐศาสตร์ เศรษฐศาสตร์มักจะวิเคราะห์ระบบสมการหรือระบบอสมการ ได้แก่ อุปสงค์และอุปทานที่มีสมมติฐานว่าอยู่ในจุดสมดุล (equilibrium) ดังนั้นในสาขาเศรษฐมิติจึงได้พัฒนาวิธีสำหรับการระบุ (identification) และการประมาณค่าแบบจำลองที่เป็นสมการพร้อมกัน (simultaneous-equation models) วิธีการเหล่านี้อาจจะช่วยนักวิจัยประมาณค่าแบบจำลองและค้นหาผลลัพธ์เชิงประจักษ์โดยปราศจากการเข้าไปเกี่ยวข้องกับระบบ

วิธีทางสถิติอย่างหนึ่งที่ใช้โดยนักเศรษฐมิติคือ วิธีถดถอย วิธีถดถอยมีความสำคัญในเศรษฐมิติเพราะนักเศรษฐศาสตร์โดยทั่วไปไม่ค่อยได้ใช้การทดลองที่ความคุมได้ นักเศรษฐมิติมักจะใช้การทดลองโดยธรรมชาติ (natural experiments) อย่างไรก็ตามข้อมูลโดยธรรมชาติที่สังเกตได้มักจะเผชิญปัญหาความเอนเอียงของตัวแปรที่ละทิ้ง (omitted-variable bias) และปัญหาอื่นๆได้แก่ความเป็นเหตุเป็นผลของกันและกัน

ตัวอย่าง

ตัวอย่างอย่างง่ายของการสร้างความสัมพันธ์ทางเศรษฐมิติในเศรษฐศาสตร์แรงงาน คือ

$\ln {\text{(wage)}}$ = $\beta _{0}$ + $\beta _{1}\ {\text{years of education}}$ + $\varepsilon$

ตัวอย่างนี้สมมติว่ารายได้ของแต่ละคนในรูปลอการิทึมธรรมชาติเป็นฟังก์ชันเชิงเส้นของจำนวนปีที่ใช้ในการศึกษาที่แต่ละคนได้รับ พารามิเตอร์ $\beta _{1}$ วัดการเพิ่มขึ้นของค่าจ้างในรูปของลอการิทึมธรรมชาติเมื่อจำนวนปีในการศึกษาเพิ่มขึ้นหนึ่งปี และค่า $\varepsilon$ เป็นตัวแปรสุ่มแสดงถึงปัจจัยอื่นๆ ที่อาจจะมีผลกระทบโดยตรงต่อค่าจ้าง เป้าหมายทางเศรษฐมิติคือการประมาณค่าพารามิเตอร์ $\beta _{0}$ และ $\beta _{1}$ ภายใต้สมมติฐานบางอย่างที่เกี่ยวกับตัวแปรสุ่ม $\varepsilon$ ตัวอย่างเช่น ถ้า $\varepsilon$ ไม่มีความสัมพันธ์กับจำนวนปีที่การศึกษา สมการนี้จะสามารถประมาณการได้โดยใช้วิธีการกำลังสองน้อยที่สุด

ถ้านักวิจัยสามารถสุ่มประชากรให้มีระดับการศึกษาที่แตกต่างกันได้ ข้อมูลที่มีจะสามารถประมาณผลของการเปลี่ยนแปลงของจำนวนปีที่ใช้ในการเรียนต่อค่าจ้างได้ แต่ในความเป็นจริง การทดลองเช่นนี้ไม่สามารถทำได้ ดังนั้น นักเศรษฐมิติจึงใช้จำนวนปีในการศึกษาและค่าจ้างที่แต่ละคนได้รับ ซึ่งแต่ละคนนั้นมีความแตกต่างในหลายๆ มิติ หากมีข้อมูลเช่นนี้ ค่าสัมประสิทธิ์ที่ประมาณค่าได้ของจำนวนปีในการเรียนในสมการข้างต้นจะสะท้อนทั้งผลของการศึกษาต่อรายได้ และผลของตัวแปรอื่นๆ ต่อรายได้ ถ้าตัวแปรอื่นๆ เหล่านั้นมีความสัมพันธ์กับการศึกษา ตัวอย่างเช่น คนที่เกิดในบางพื้นที่อาจจะได้รับรายได้ที่สูงและมีการศึกษาที่สูง หากนักเศรษฐมิติไม่ควบคุมผลของสถานที่เกิดในสมการข้างต้น ผลของสถานที่เกิดต่อค่าจ้างอาจส่งกระทบให้เกิดความผิดเพี้ยนต่อผลของการศึกษาต่อค่าจ้าง

ทางที่ดีและเป็นที่นิยมที่สุดคือการควบคุมสถานที่เกิดโดยเพิ่มผลของสถานที่เกิดเข้าไปในสมการข้างต้นด้วย การละเลยสถานที่เกิด และสมมติฐานที่ว่า $\varepsilon$ ไม่มีความสัมพันธ์ต่อการศึกษาส่งผลให้เกิดแบบจำลองที่ผิดพลาด อีกวิธีหนึ่งที่นิยมคือการเพิ่มตัวแปรที่มีความสัมพันธ์ร่วมที่ไม่ใช่ตัวแปรเครื่องมือเข้าไปในสมการเพื่อทำให้สามารถหาค่า $\beta _{1}$ ได้ ภาพรวมของการใช้วิธีทางเศรษฐมิติที่ใช้ศึกษาปัญหานี้พบได้ใน Card (1999)

วารสาร

วารสารหลักที่ตีพิมพ์งานเกี่ยวกับเศรษฐมิติ ได้แก่ Econometrica, the Journal of Econometrics, the Review of Economics and Statistics, Econometric Theory, the Journal of Applied Econometrics, Econometric Reviews, the Econometrics Journal ^[6], Applied Econometrics and International Development, the Journal of Business & Economic Statistics

ข้อจำกัดและข้อวิจารณ์

เช่นเดียวกับรูปแบบการวิเคราะห์สถิติอื่นๆ แบบจำลองเศรษฐมิติที่ไม่ดีอาจจะแสดงความสัมพันธ์หลอก ซึ่งหมายถึงตัวแปรสองตัวแปรมีความสัมพันธ์กันแต่ไม่ได้มีความเป็นเหตุเป็นผลกัน ในการศึกษาเกี่ยวกับการใช้เศรษฐมิติในวารสารทางเศรษฐศาสตร์ที่สำคัญ แมคโคลสคีย์สรุปว่าเศรษฐกรบางคนนำเสนอค่าพี (ซึ่งตามธรรมเนียมปฏิบัติแบบฟิชเชอร์ในด้านการทดสอบนัยสำคัญของสมมติฐานหลักแบบจุด) และละเลยปัญหาความผิดพลาดแบบที่สอง เศรษฐกรบางคนไม่สมาถนำเสนอผลการประมาณการของขนาดของผลกระทบที่เกิดขึ้นได้ (นอกเหนือไปจากนัยสำคัญทางสถิติ) และอภิปรายความสำคัญในทางเศรษฐศาสตร์ เธอยังอ้างว่าเศรษฐกรบางคนไม่สามารถที่จะใช้เหตุผลในทางเศรษฐศาสตร์ในการเลือกแบบจำลอง โดยเฉพาะการตัดสินใจว่าตัวแปรใดที่ควรใส่ในสมการถดถอย

อ้างอิง

↑ ^1.0 ^1.1 Geweke, John; Horowitz, Joel; Pesaran, Hashem (2018). "Econometrics". The New Palgrave Dictionary of Economics (3 ed.). Palgrave Macmillan. pp. 3199–3242. doi:10.1057/978-1-349-95189-5. ISBN 9781349951888.
↑ Greene, William (2012). Econometric Analysis (7th ed.). Pearson Education. pp. 34, 41–42. ISBN 9780273753568.
↑ Greene (2012), 12.
↑ Clive Granger (2008). "forecasting," The New Palgrave Dictionary of Economics, 2nd Edition. Abstract.
↑ Wooldridge, Jeffrey (2013). Introductory Econometrics, A modern approach. South-Western, Cengage learning. ISBN 978-1-111-53104-1.
↑ "The Econometrics Journal - Wiley Online Library". Wiley.com. คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2011-10-06. สืบค้นเมื่อ 2013-10-08.

[Palgrave-1] 1.0 ^1.1 Geweke, John; Horowitz, Joel; Pesaran, Hashem (2018). "Econometrics". The New Palgrave Dictionary of Economics (3 ed.). Palgrave Macmillan. pp. 3199–3242. doi:10.1057/978-1-349-95189-5. ISBN 9781349951888.

[Greene-2] Greene, William (2012). Econometric Analysis (7th ed.). Pearson Education. pp. 34, 41–42. ISBN 9780273753568.

[3] Greene (2012), 12.

[4] Clive Granger (2008). "forecasting," The New Palgrave Dictionary of Economics, 2nd Edition. Abstract.

[Introductory_econometrics-5] Wooldridge, Jeffrey (2013). Introductory Econometrics, A modern approach. South-Western, Cengage learning. ISBN 978-1-111-53104-1.

[6] "The Econometrics Journal - Wiley Online Library". Wiley.com. คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2011-10-06. สืบค้นเมื่อ 2013-10-08.

[1]

[2]

[3]

[4]

[5]

[6]