สมบัติการสลับที่
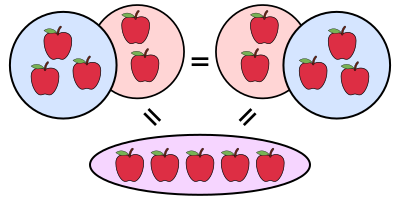
ในคณิตศาสตร์ สมบัติการสลับที่ (อังกฤษ: commutativity) คือกระบวนการเปลี่ยนลำดับของบางสิ่ง โดยไม่ทำให้ผลลัพธ์สุดท้ายเปลี่ยนแปลง เป็นสมบัติเบื้องต้นของการดำเนินการทางคณิตศาสตร์หลายชนิด และการพิสูจน์หลายอย่างก็ขึ้นอยู่กับสมบัตินี้
สมบัติการสลับที่ของการดำเนินการพื้นฐาน อาทิการบวกหรือการคูณของจำนวน ถูกสมมติขึ้นโดยไร้ข้อกังขามาเป็นเวลายาวนาน และสมบัตินี้ไม่เคยมีการตั้งชื่อหรือการให้เหตุผลจนกระทั่งคริสต์ศตวรรษที่ 19 ซึ่งเป็นช่วงเวลาที่นักคณิตศาสตร์เริ่มจัดระเบียบแบบแผนของทฤษฎีต่าง ๆ ทางคณิตศาสตร์
การใช้ทั่วไป
[แก้]สมบัติการสลับที่ (หรือกฎการสลับที่) เป็นสมบัติที่เกี่ยวข้องกับการดำเนินการทวิภาคและฟังก์ชัน และในทางเดียวกัน ถ้าสมบัติการสลับที่มีอยู่สำหรับสมาชิกคู่หนึ่ง ภายใต้การดำเนินการทวิภาคที่แน่นอนแล้ว เราจะกล่าวได้ว่าสมาชิกสองตัวนั้นสามารถสลับที่ (commute) บนการดำเนินการดังกล่าว
ในทฤษฎีกรุปและทฤษฎีเซต เราจะเรียกโครงสร้างเชิงพีชคณิตว่าเป็นโครงสร้างสลับที่ได้ (commutative) เมื่อมีตัวดำเนินการที่แน่นอนทำให้เกิดสมบัติการสลับที่ ในสาขาทางคณิตศาสตร์ที่สูงขึ้นไป เช่นคณิตวิเคราะห์หรือพีชคณิตเชิงเส้น สมบัติการสลับที่ของการดำเนินการที่รู้จักเป็นอย่างดี (อย่างการบวกและการคูณของจำนวนจริงและจำนวนเชิงซ้อน) มักจะมีการใช้งานมาก (หรือสมมติขึ้นมา) ในการพิสูจน์ต่าง ๆ [1][2]
นิยาม
[แก้]คำว่า สลับที่ (commute) หรือ สลับที่ได้ (commutative) มีการใช้งานในหลายประเด็นดังนี้ [3][4]
- กำหนดการดำเนินการทวิภาค ∗ บนเซต S เราจะกล่าวว่าการดำเนินการนั้น สลับที่ได้ ถ้าหาก
- ส่วนการดำเนินการที่ไม่เป็นไปตามเงื่อนไขด้านบน จะถือว่าเป็นการดำเนินการที่ สลับที่ไม่ได้ หรือ ไม่สลับที่ (non-commutative)
- เราอาจกล่าวได้ว่า x สามารถ สลับที่ กับ y ภายใต้การดำเนินการ ∗ ถ้าหาก
- กำหนดฟังก์ชันทวิภาค f : A×A → B เราจะกล่าวว่าฟังก์ชันนั้น สลับที่ได้ ถ้าหาก
ตัวอย่าง
[แก้]การดำเนินการสลับที่ได้ในชีวิตประจำวัน
[แก้]- การใส่รองเท้าก็เหมือนกับการดำเนินการสลับที่ได้ เพราะไม่สำคัญว่าจะใส่รองเท้าข้างซ้ายหรือข้างขวาก่อน ผลสุดท้ายก็เหมือนกันคือได้ใส่รองเท้าทั้งสองข้าง
- ในการแลกเปลี่ยนเงินตรา เราสามารถใช้ประโยชน์จากสมบัติการสลับที่ของการบวก ซึ่งไม่สำคัญว่าเราจะแลกเปลี่ยนอะไรก่อน ผลลัพธ์สุดท้ายก็จะรวมกันได้เท่าเดิม
การดำเนินการสลับที่ได้ในคณิตศาสตร์
[แก้]ตัวอย่างการดำเนินการทวิภาคที่มีสมบัติการสลับที่ ซึ่งเป็นที่รู้จักกันดีได้แก่ [3]
- การบวกของจำนวนจริง สลับที่ได้เนื่องจาก
- ตัวอย่างเช่น 4 + 5 = 5 + 4 ซึ่งนิพจน์ทั้งสองข้างมีค่าเท่ากับ 9
- การคูณของจำนวนจริง สลับที่ได้เนื่องจาก
- ตัวอย่างเช่น 3 × 5 = 5 × 3 ซึ่งนิพจน์ทั้งสองข้างมีค่าเท่ากับ 15
ตัวอย่างการดำเนินการอื่น ๆ เช่น การบวกและการคูณของจำนวนเชิงซ้อน การบวกของเวกเตอร์ อินเตอร์เซกชันและยูเนียนของเซต เป็นต้น
การดำเนินการสลับที่ไม่ได้ในชีวิตประจำวัน
[แก้]
- การซักผ้าและการตากผ้าก็เหมือนกับการดำเนินการสลับที่ไม่ได้ เพราะถ้าหากเราตากผ้าก่อนซักผ้า ผลลัพธ์จะต่างไปจากที่เราซักผ้าก่อนแล้วค่อยตาก คือผ้าเปียกหรือไม่เปียกน้ำ
- ลูกบาศก์ของรูบิคไม่สามารถสลับที่ได้ เช่น ถ้าหากบิดส่วนหน้าตามเข็มนาฬิกา ส่วนบนตามเข็ม และส่วนหน้าทวนเข็ม (FUF') หน้าบนลูกบาศก์จะให้ผลไม่เหมือนกับการบิดส่วนหน้าตามเข็ม และบิดทวนเข็มกลับ ตามด้วยส่วนบนตามเข็ม (FF'U) ลำดับการบิดลูกบาศก์ของรูบิคจึงสลับที่ไม่ได้ เป็นกรณีหนึ่งที่มีการศึกษาในทฤษฎีกรุป
การดำเนินการสลับที่ไม่ได้ในคณิตศาสตร์
[แก้]ตัวอย่างการดำเนินการทวิภาคที่ไม่มีสมบัติการสลับที่เช่น [5]
โครงสร้างทางคณิตศาสตร์อื่น ๆ
[แก้]- อาบีเลียนกรุป คือกรุปที่มีการดำเนินการของกรุป ที่สลับที่ได้ [2]
- ริงสลับที่ คือริงที่มีการคูณ ที่สลับที่ได้ (สำหรับการบวกนั้นสลับที่ได้อยู่แล้วตามนิยาม) [2]
- ในฟีลด์หนึ่ง ๆ ทั้งการบวกและการคูณสามารถสลับที่ได้ [2]
อ้างอิง
[แก้]- ↑ Axler, Sheldon (1997). Linear Algebra Done Right, 2e. Springer. ISBN 0-387-98258-2.
- ↑ 2.0 2.1 2.2 2.3 Gallian, Joseph (2006). Contemporary Abstract Algebra, 6e. ISBN 0-618-51471-6.
- ↑ 3.0 3.1 Krowne, Aaron, Commutative ที่ PlanetMath., เข้าถึงเมื่อ 8 สิงหาคม 2550.
- ↑ เอริก ดับเบิลยู. ไวส์สไตน์, "Commute" จากแมทเวิลด์., เข้าถึงเมื่อ 8 สิงหาคม 2550.
- ↑ Yark. Examples of non-commutative operations ที่ PlanetMath., เข้าถึงเมื่อ 8 สิงหาคม 2550.
ดูเพิ่ม
[แก้]- สมบัติการสลับที่กลับเครื่องหมาย (anticommutativity)
- สมบัติการเปลี่ยนหมู่
- สมบัติการแจกแจง






