ผู้ใช้:Keeplearn/กระบะทราย2ExteriorAlgebra

"Wedge product" เปลี่ยนทางมาที่นี่ สำหรับthe wedge sum, sometimes called wedge product, in Topology ดูที่ wedge sum

การตีความเชิงเรขาคณิตสำหรับพีชคณิตภายนอกของ n เวกเตอร์ (u, v, w) ในการหา n-เวกเตอร์ (สมาชิกรูปทรงขนาน) ซึ่ง n = อันดับ, สำหรับ n = 1, 2, 3. "การหมุนเวียน"แสดงทิศทางของปริภูมิเวกเตอร์.

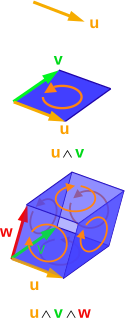
ในทางคณิตศาสตร์ ผลคูณภายนอก หรือ ผลคูณเวดจ์ ของเวกเตอร์ คือโครงสร้างหนึ่งทางพีชคณิตที่เราใช้ในเรขาคณิตแบบยูคลิดเพื่อที่จะศึกษาพื้นที่, ปริมาตร, และปริมาณอื่นๆ ที่มีมิติที่สูงกว่า ผลคูณภายนอกของสองเวกเตอร์ u และ v เขียนแทนด้วย u ∧ v (ยู เวดจ์ วี) เรียกว่า ไบเวกเตอร์ และอยู่ในปริภูมิหนึ่งที่เราเรียกว่ากำลังสองภายนอก (เอกซทีเรียร์สแควร์) ซึ่งเป็นปริภูมิเวกเตอร์ทางเรขาคณิตที่แตกต่างจากปริภูมิตั้งต้นของเวกเตอร์ เราตีความขนาด ของผลคูณ u ∧ v เป็นพื้นที่ของสี่เหลี่ยมด้านขนานที่มีด้านเป็น u และ v ซึ่งเราคำนวณได้โดยการใช้ผลคูณครอสส์ของสองเวกเตอร์ในสามมิติ ผลคูณภายนอกมีสมบัติต่อต้านการสลับที่เหมือนกับผลคูณครอสส์ ซึ่งหมายความว่า u ∧ v = −(v ∧ u) สำหรับทุกเวกเตอร์ u และ v วิธีหนึ่งที่จะจินตนาการถึงไบเวกเตอร์คือกลุ่มของสี่เหลี่ยมด้านขนานซึ่งทั้งหมดอยู่ในระนาบเดียวกัน มีพื้นที่เหมือนกัน และมีทิศทางของขอบเขตเหมือนกัน โดยที่อาจมีทิศทางตามเข็ม หรือ ทวนเข็มก็ได้

เมื่อเราพิจารณาผลคูณภายนอกในลักษณะนี้ เราจะเรียกผลคูณภายนอกของสองเวกเตอร์ว่า 2-เบลด และเราจะนิยามรูปแบบทั่วไปของผลคูณภายนอกของ k เวกเตอร์และเรียกมันว่า k-เบลด ซึ่งอยู่ในปริภูมิเรขาคณิตที่เราเรียกว่าปริภูมิภายนอกอันดับที่ k ขนาดของผลคูณ k-เบลดคือปริมาณของรูปทรงขนานมิติที่ k ที่มีด้านขอบเป็นเวกเตอร์ตั้งต้น ซึ่งเหมือนกันกับขนาดของผลคูณเชิงสเกลาร์ของสามเวกเตอร์ในสามมิติที่ให้ปริมาตรของรูปทรงขนานที่เป็นส่วนขยายของเวกเตอร์เหล่านั้น

พีชคณิตภายนอก หรือ พีชคณิตของกรัสส์แมน ตั้งชื่อตามแฮร์มันน์ กรัสส์มันน์, เป็นระบบพีชคณิตที่ผลลัพธ์ของมันคือผลคูณภายนอกปริภูมิตั้งต้น พีชคณิตภายนอกให้สภาพแวดล้อมเพื่อตอบคำถามทางเรขาคณิต ตัวอย่างเช่น เบลดมีความหมายทางเรขาคณิตที่ชัดเจน เราสามารถจัดการกับวัตถุในพีชคณิตภายนอกตามชุดของกฎที่ชัดเจน พีชคณิตภายนอกประกอบด้วย k-เบลด และผลรวมของk-เบลดที่เราเรียกว่า''k''-เวกเตอร์. เราเรียกk-เบลดว่าสมาชิกมูลฐานของพีชคณิตภายนอกเพราะพวกมันเป็นผลลัพธ์มูลฐานของเวกเตอร์ เรานิยามrankของk-เวกเตอร์ใดๆ ว่าเป็นจำนวนที่เล็กที่สุดของสมาชิกมูลฐานที่ประกอบขึ้นเป็นผลรวม เราได้ขยายผลคูณภายนอกออกไปเพื่อให้ได้พีชคณิตภายนอกที่สมบูรณ์แบบเพื่อให้เราสามารถคูณสมาชิกใดๆของมันสองตัวได้อย่างมีเหตุมีผล ด้วยการเพิ่มผลคูณแบบนี้ให้กับพีชคณิตภายนอก ทำให้พีชคณิตภายนอกเป็นพีชคณิตการเปลี่ยนหมู่ (associative algebra) ซึ่งหมายความว่า α ∧ (β ∧ γ) = (α ∧ β) ∧ γ สำหรับสมาชิกใดๆ α, β, γ k-เวกเตอร์มีอันดับที่k หมายถึงพวกมันเป็นผลรวมของผลคูณของเวกเตอร์kตัว เมื่อนำสมาชิกที่มีอันดับต่างกันมาคูณกัน เราจะเอาอันดับของมันมาบวกกันเหมือนการคูณของพหุคูณ (polynomials) สิ่งนี้หมายความว่าพีชคณิตภายนอกเป็นพีชคณิตเชิงอันดับ (graded algebra)

ตามความรู้สึกในเชิงโครงสร้างสากล (universal construction) พีชคณิตภายนอกเป็นพีชคณิตที่ใหญ่ที่สุดที่รองรับผลคูณแบบอื่นของเวกเตอร์และเราสามารถนิยามมันในรูปของวัตถุอื่นที่เรารู้จักเช่น เทนเซอร์ (Tensors) นิยามของพีชคณิตภายนอกใช้ได้กับปริภูมิหลายแบบไม่ใช่แค่ปริภูมิเวกเตอร์เชิงเรขาคณิต แต่ใช้ได้กับวัตถุอื่นที่เหมือนเวกเตอร์ เช่น สนามเวกเตอร์ (vector field) หรือ ฟังก์ชันเวกเตอร์ (vector function) โดยทั่วไป เราสามารถนิยามพีชคณิตภายนอกสำหรับส่วนจำเพาะ (module) บนวงแหวนสับเปลี่ยน (commutative ring) และสำหรับโครงสร้างอื่นที่เราสนใจในพีชคณิตเชิงทฤษฎี (abstract algebra) โครงสร้างทั่วไปแบบหนึ่งที่เราใช้พีชคณิตภายนอกกับงานที่สำคัญที่สุดอย่างหนึ่งคือ พีชคณิตของอนุพันธ์ (differential forms) ซึ่งเป็นพื้นฐานของเรขาคณิตเชิงอนุพันธ์ (differential geometry) อนุพันธ์เป็นวัตถุทางคณิตศาสตร์ซึ่งแสดงให้เห็นภาพบริเวณที่เล็กมากจนวัดไม่ได้ซึ่งวัตถุยังคงคุณสมบัตเฉพาะตัว (infinitesimal areas) ของรูปทรงขนานที่เล็กมากจนวัดไม่ได้ (และรูปทรงที่มิติสูงกว่า) และดังนั้นเราสามารถหาปริพันธ์ (integrate) ของมันบนพื้นผิวและรูปทรง (manifolds) ที่มีมิติที่สูงกว่า ในทางที่จะวางนัยทั่วไปให้ปริพันธ์เชิงเส้น (line integral) จากแคลคูลัส พีชคณิตเชิงเส้นก็มีคุณสมบัติทางพีชคณิตหลายอย่างซึ่งทำให้มันเป็นเครื่องมือที่ใช้งานได้สะดวกในพีชคณิต การรวมกันของพีชคณิตภายนอกกับปริภูมิเวกเตอร์อันหนึ่งคือรูปแบบหนึ่งของฟังก์เตอร์ (functor) บนปริภูมิเวกเตอร์ ซึ่งหมายถึงมันเข้ากันได้กับการแปลงเชิงเส้นของปริภูมิเวกเตอร์ พีชคณิตภายนอกเป็นตัวอย่างหนึ่งของพีชคณิตเชิงคู่ (bialgebra) ซึ่งหมายความว่าปริภูมิที่คู่กันของมัน (dual space) ก็มีผลคูณด้วยและผลคูณที่คู่กันนี้เข้ากันได้กับผลคูณภายนอก พีชคณิตเชิงคู่คือพีชคณิตของรูปแบบเชิงหลายเส้นอื่นๆ (alternating multilinear forms) บน ปริภูมิV, และการจับคู่กันระหว่างพีชคณิตภายนอกกับคู่ของมันคือผลคูณภายใน (interior product)

ตัวอย่างจูงใจ

พื้นที่ในระนาบ

พื้นที่ของสี่เหลี่ยมด้านขนานในนิพจน์ของตัวกำหนดของเมทริกซ์ของพิกัดของจุดยอดของมันสองจุด

ระนาบคาร์ทีเซียน (Cartesian plane) R² เป็นปริภูมิเวกเตอร์ที่ประกอบด้วยส่วนประกอบมูลฐานคือเวกเตอร์หนึ่งหน่วยคู่หนึ่ง

${\mathbf {e} }_{1}={\begin{bmatrix}1\\0\end{bmatrix}},\quad {\mathbf {e} }_{2}={\begin{bmatrix}0\\1\end{bmatrix}}.$

สมมติว่า

${\mathbf {v} }={\begin{bmatrix}a\\b\end{bmatrix}}=a{\mathbf {e} }_{1}+b{\mathbf {e} }_{2},\quad {\mathbf {w} }={\begin{bmatrix}c\\d\end{bmatrix}}=c{\mathbf {e} }_{1}+d{\mathbf {e} }_{2}$

เป็นเวกเตอร์คู่หนึ่งที่กำหนดมาให้ในปริภูมิ R², มีสี่เหลี่ยมด้านขนานรูปหนึ่งที่ไม่เหมือนใครที่มีเวกเตอร์ v และ w เป็นด้านทั้งสองของมัน พื้นที่ของสี่เหลี่ยมด้านขนานนี้หาได้จากสูตรมาตรฐานของตัวกำหนดเมทริกซ์ (ดีเทอร์มิแนนต์):

${\text{Area}}=\left|\det {\begin{bmatrix}{\mathbf {v} }&{\mathbf {w} }\end{bmatrix}}\right|=\left|\det {\begin{bmatrix}a&c\\b&d\end{bmatrix}}\right|=\left|ad-bc\right|.$

ตอนนี้ พิจารณาผลคูณภายนอกของ v และ w:

${\begin{aligned}{\mathbf {v} }\wedge {\mathbf {w} }&=(a{\mathbf {e} }_{1}+b{\mathbf {e} }_{2})\wedge (c{\mathbf {e} }_{1}+d{\mathbf {e} }_{2})\\&=ac{\mathbf {e} }_{1}\wedge {\mathbf {e} }_{1}+ad{\mathbf {e} }_{1}\wedge {\mathbf {e} }_{2}+bc{\mathbf {e} }_{2}\wedge {\mathbf {e} }_{1}+bd{\mathbf {e} }_{2}\wedge {\mathbf {e} }_{2}\\&=(ad-bc){\mathbf {e} }_{1}\wedge {\mathbf {e} }_{2}\end{aligned}}$

โดยขั้นตอนแรกใช้กฏการกระจายสำหรับผลคูณภายนอก และขั้นตอนสุดท้ายใช้คุณสมบัติการสลับที่ของผลคูณภายนอกคือ e₂ ∧ e₁ = −e₁ ∧ e₂ สังเกตว่าสัมประสิทธิ์ในนิพจน์สุดท้ายคือตัวกำหนดของเมทริกซ์ [v w] ข้อเท็จจริงที่ว่ามันอาจเป็นบวกหรือลบมีความหมายเป็นนัยว่า v และ w อาจมีทิศทวนเข็มหรือตามเข็มในฐานะจุดยอดของสี่เหลี่ยมด้านขนานที่พวกมันกำหนด เราเรียกพื้นที่แบบนี้ว่า พื้นที่มีเครื่องหมาย ของสี่เหลี่ยมด้านขนาน: ค่าสัมบูรณ์ของพื้นที่มีเครื่องหมายคือพื้นที่ธรรมดาและเครื่องหมายกำหนดทิศทางของมัน

ความจริงที่ว่าค่าสัมประสิทธิ์นี้คือพื้นที่มีเครื่องหมายไม่ใช่ความบังเอิญ ความจริงแล้ว เราจะเห็นได้อย่างง่ายๆ ว่าผลคูณภายนอกควรจะเกี่ยวข้องกับพื้นที่มีเครื่องหมาย ถ้าใครสักคนพยายามที่จะพิสูจน์สัจพจน์กับพื้นที่นี้ในฐานะเป็นโครงสร้างพีชคณิต โดยละเอียดคือ ถ้า A(v, w) แสดงถึงพื้นที่มีเครื่องหมายของสี่เหลี่ยมด้านขนานที่ถูกกำหนดด้วยคู่ของเวกเตอร์ v และ w แล้ว พื้นที่ A ต้องสอดคล้องกับคุณสมบัติต่อไปนี้:

1. A(jv, kw) = j k A(v, w) สำหรับจำนวนจริงใดๆ j และ k เนื่องจากการปรับมาตราส่วนของด้านเป็นการปรับมาตราส่วนของพื้นที่ด้วยปริมาณเหมือนกัน (และการกลับทิศทางของด้านหนึ่งด้านเป็นการกลับทิศทางของสี่เหลี่ยมด้านขนานด้วย)
2. A(v,v) = 0 เนื่องจากพื้นที่ของสี่เหลี่ยมด้านขนานลดรูป (degenerate) ถูกกำหนดด้วยเวกเตอร์ v นั่นคือส่วนตัดเชิงเส้น (line segment) เป็นศูนย์
3. A(w,v) = −A(v,w) เนื่องจากการสลับตำแหน่งของเวกเตอร์ v และ w กลับทิศทางของสี่เหลี่ยมด้านขนาน
4. A(v + jw,w) = A(v,w) สำหรับจำนวนจริงใดๆ j เนื่องจากการบวกส่วนขยายของเวกเตอร์ w เข้ากับเวกเตอร์ v ไม่กระทบทั้งฐานและความสูงของสี่เหลี่ยมด้านขนานและดังนั้นพื้นที่ของมันยังคงเดิม
5. A(e₁, e₂) = 1 เนื่องจากพื้นที่ของตารางหนึ่งหน่วยคือหนึ่ง

ด้วยข้อยกเว้นของคุณสมบัติข้อสุดท้าย จะเห็นว่าผลคูณภายนอกสอดคล้องกับคุณสมบัติอย่างเป็นทางการในฐานะพื้นที่ ในแง่หนึ่งผลคูณภายนอกสรุปคุณสมบัติสุดท้ายโดยการยอมให้เปรียบเทียบพื้นที่ของสี่เหลี่ยมด้านขนานรูปหนึ่งกับพื้นที่ของสี่เหลี่ยมด้านขนาน"มาตรฐาน"ใดๆ ที่เราเลือก (ในที่นี้คือ สี่เหลี่ยมด้านขนานที่ประกอบด้วยด้าน e₁ และ e₂). อีกแง่หนึ่งคือผลคูณภายนอกในสองมิติให้สูตรพื้นฐาน-อิสระของพื้นที่

ผลคูณไขว้และผลคูณสามเวกเตอร์

ผลคูณไขว้ (เวกเตอร์สีน้ำเงิน) เกี่ยวข้องกับผลคูณภายนอก(สี่เหลี่ยมด้านขนานสีน้ำเงินอ่อน)......... ความยาวของผลคูณไขว้คือความยาวของเวกเตอร์หนึ่งหน่วย(สีแดง) โดยที่ขนาดของผลคูณภายนอกคือขนาดของสี่เหลี่ยมด้านขนานที่อ้างอิง (สีแดงอ่อน).

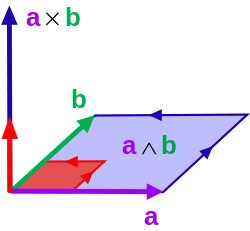
สำหรับเวกเตอร์ในปริภูมิ R³, พีชคณิตภายนอกเกี่ยวข้องอย่างมากกับผลคูณไขว้(ผลคูณสองเวกเตอร์) และผลคูณสามเวกเตอร์ การใช้สมาชิกมูลฐาน {e₁, e₂, e₃} แสดงผลคูณภายนอกของเวกเตกเตอร์คู่หนึ่ง

$\mathbf {u} =u_{1}\mathbf {e} _{1}+u_{2}\mathbf {e} _{2}+u_{3}\mathbf {e} _{3}$

และ

$\mathbf {v} =v_{1}\mathbf {e} _{1}+v_{2}\mathbf {e} _{2}+v_{3}\mathbf {e} _{3}$

คือ

$\mathbf {u} \wedge \mathbf {v} =(u_{1}v_{2}-u_{2}v_{1})(\mathbf {e} _{1}\wedge \mathbf {e} _{2})+(u_{3}v_{1}-u_{1}v_{3})(\mathbf {e} _{3}\wedge \mathbf {e} _{1})+(u_{2}v_{3}-u_{3}v_{2})(\mathbf {e} _{2}\wedge \mathbf {e} _{3})$

โดยที่ {e₁ ∧ e₂, e₃ ∧ e₁, e₂ ∧ e₃} เป็นสมาชิกมูลฐานสำหรับปริภูมิ Λ²(R³) ค่าสัมประสิทธิ์ข้างต้นเหมือนกับค่าในนิยามตามปกติของผลคูณไขว้ของเวกเตอร์ในสามมิติ ความแตกต่างเพียงอย่างเดียวคือผลคูณภายนอกไม่ได้เป็นเวกเตอร์ธรรมดาหนึ่งเวกเตอร์ แต่มันเป็นวัตถุสองเวกเตอร์ (วัตถุหนึ่งที่ประกอบด้วยสองเวกเตอร์)

นำเวกเตอร์ตัวที่สามเข้ามา

$\mathbf {w} =w_{1}\mathbf {e} _{1}+w_{2}\mathbf {e} _{2}+w_{3}\mathbf {e} _{3},$

ผลคูณภายนอกของสามเวกเตอร์คือ

$\mathbf {u} \wedge \mathbf {v} \wedge \mathbf {w} =(u_{1}v_{2}w_{3}+u_{2}v_{3}w_{1}+u_{3}v_{1}w_{2}-u_{1}v_{3}w_{2}-u_{2}v_{1}w_{3}-u_{3}v_{2}w_{1})(\mathbf {e} _{1}\wedge \mathbf {e} _{2}\wedge \mathbf {e} _{3})$

โดยที่ e₁ ∧ e₂ ∧ e₃ เป็นเวกเตอร์มูลฐานสำหรับปริภูมิ Λ³(R³) ค่าสัมประสิทธิ์สเกลาร์คือผลคูณสามเวกเตอร์

เราสามารถแปลผลคูณไขว้และผลคูณสามเวกเตอร์ในสามมิติทั้งในเชิงเรขาคณิตและพีชคณิต เราแปลผลคูณไขว้ u × v ว่าเป็นเวกเตอร์หนึ่งซึ่งตั้งฉากกับเวกเตอร์ u และ v และขนาดของมันเท่ากับพื้นที่ของสี่เหลี่ยมด้านขนานที่กำหนดโดยทั้งสองเวกเตอร์ เรายังสามารถแปลว่ามันเป็นเวกเตอร์ที่ประกอบด้วยไมเนอร์ (minors) ของเมทริกซ์ที่ประกอบด้วยเวกเตอร์หลักแนวตั้ง u และ v ผลคูณสามเวกเตอร์ของ u v และ w ในเชิงเรขาคณิตคือปริมาตร(ที่มีเครื่องหมาย) ในเชิงพีชคณิต มันคือตัวกำหนดของเมทริกซ์ที่ประกอบด้วยเวกเตอร์หลักแนวตั้ง u v และ w เราสามารถแปลความหมายของผลคูณภายนอกในสามมิติในแบบเดียวกัน ความจริงแล้วการปรากฏตัวของสมาชิกมูลฐานเชิงตั้งฉากเชิงบวก (Orthonormal basis) ของผลคูณภายนอกได้สรุปความคิดเหล่านี้ไว้ในฐานะเป็นมิติที่สูงขึ้น

นิยามอย่างเป็นทางการและคุณสมบัติเชิงพีชคณิต

พีชคณิตภายนอก Λ(V) บนปริภูมิเวกเตอร์ V บนสนามเวกเตอร์ (field) K ถูกนิยามว่าเป็นพีชคณิตผลหาร (quotient algebra) ของพีชคณิตเทนเซอร์ (tensor algebra) ด้วยเซตอุดมคติ (the two-sided ideal) I ที่ประกอบด้วยสมาชิกทุกสมาชิกของรูปแบบ x ⊗ x ซึ่ง x ∈ V. แสดงเป็นสัญลักษณ์,

$\Lambda (V):=T(V)/I.\,$

ผลคูณภายนอก ∧ ของสมาชิกสองตัวของปริภูมิ Λ(V) ถูกนิยามโดย

$\alpha \wedge \beta =\alpha \otimes \beta {\pmod {I}}.$

Anticommutativity of the exterior product

The exterior product is alternating on elements of V, which means that x ∧ x = 0 for all x ∈ V. It follows that the product is also anticommutative on elements of V, for supposing that x, y ∈ V,

$0=(x+y)\wedge (x+y)=x\wedge x+x\wedge y+y\wedge x+y\wedge y=x\wedge y+y\wedge x$

hence

$x\wedge y=-y\wedge x.$

Conversely, it follows from the anticommutativity of the product that the product is alternating, unless K has characteristic two.

More generally, if x₁, x₂, ..., x_k are elements of V, and σ is a permutation of the integers [1,...,k], then

$x_{\sigma (1)}\wedge x_{\sigma (2)}\wedge \dots \wedge x_{\sigma (k)}=\operatorname {sgn} (\sigma )x_{1}\wedge x_{2}\wedge \dots \wedge x_{k},$

where sgn(σ) is the signature of the permutation σ.

The exterior power

The kth exterior power of V, denoted Λ^k(V), is the vector subspace of Λ(V) spanned by elements of the form

$x_{1}\wedge x_{2}\wedge \dots \wedge x_{k},\quad x_{i}\in V,i=1,2,\dots ,k.$

If α ∈ Λ^k(V), then α is said to be a k-vector. If, furthermore, α can be expressed as an exterior product of k elements of V, then α is said to be decomposable. Although decomposable k-vectors span Λ^k(V), not every element of Λ^k(V) is decomposable. For example, in R⁴, the following 2-vector is not decomposable:

$\alpha =e_{1}\wedge e_{2}+e_{3}\wedge e_{4}.$

(This is in fact a symplectic form, since α ∧ α ≠ 0.)

Basis and dimension

If the dimension of V is n and {e₁,...,e_n} is a basis of V, then the set

$\{e_{i_{1}}\wedge e_{i_{2}}\wedge \cdots \wedge e_{i_{k}}\mid 1\leq i_{1}<i_{2}<\cdots <i_{k}\leq n\}$

is a basis for Λ^k(V). The reason is the following: given any exterior product of the form

$v_{1}\wedge \cdots \wedge v_{k}$

then every vector v_j can be written as a linear combination of the basis vectors e_i; using the bilinearity of the exterior product, this can be expanded to a linear combination of exterior products of those basis vectors. Any exterior product in which the same basis vector appears more than once is zero; any exterior product in which the basis vectors do not appear in the proper order can be reordered, changing the sign whenever two basis vectors change places. In general, the resulting coefficients of the basis k-vectors can be computed as the minors of the matrix that describes the vectors v_j in terms of the basis e_i.

By counting the basis elements, the dimension of Λ^k(V) is equal to a binomial coefficient:

$\operatorname {dim} (\Lambda ^{k}(V))={\binom {n}{k}}$

In particular, Λ^k(V) = {0} for k > n.

Any element of the exterior algebra can be written as a sum of k-vectors. Hence, as a vector space the exterior algebra is a direct sum

$\Lambda (V)=\Lambda ^{0}(V)\oplus \Lambda ^{1}(V)\oplus \Lambda ^{2}(V)\oplus \cdots \oplus \Lambda ^{n}(V)$

(where by convention Λ⁰(V) = K and Λ¹(V) = V), and therefore its dimension is equal to the sum of the binomial coefficients, which is 2ⁿ.

Rank of a k-vector

If α ∈ Λ^k(V), then it is possible to express α as a linear combination of decomposable k-vectors:

$\alpha =\alpha ^{(1)}+\alpha ^{(2)}+\cdots +\alpha ^{(s)}$

where each α⁽ⁱ⁾ is decomposable, say

$\alpha ^{(i)}=\alpha _{1}^{(i)}\wedge \cdots \wedge \alpha _{k}^{(i)},\quad i=1,2,\dots ,s.$

The rank of the k-vector α is the minimal number of decomposable k-vectors in such an expansion of α. This is similar to the notion of tensor rank.

Rank is particularly important in the study of 2-vectors (Sternberg 1974, §III.6) (Bryant et al. 1991). The rank of a 2-vector α can be identified with half the rank of the matrix of coefficients of α in a basis. Thus if e_i is a basis for V, then α can be expressed uniquely as

$\alpha =\sum _{i,j}a_{ij}e_{i}\wedge e_{j}$

where a_ij = −a_ji (the matrix of coefficients is skew-symmetric). The rank of the matrix a_ij is therefore even, and is twice the rank of the form α.

In characteristic 0, the 2-vector α has rank p if and only if

${\underset {p}{\underbrace {\alpha \wedge \cdots \wedge \alpha } }}\not =0$

and

${\underset {p+1}{\underbrace {\alpha \wedge \cdots \wedge \alpha } }}=0.$

Graded structure

The exterior product of a k-vector with a p-vector is a (k+p)-vector, once again invoking bilinearity. As a consequence, the direct sum decomposition of the preceding section

$\Lambda (V)=\Lambda ^{0}(V)\oplus \Lambda ^{1}(V)\oplus \Lambda ^{2}(V)\oplus \cdots \oplus \Lambda ^{n}(V)$

gives the exterior algebra the additional structure of a graded algebra. Symbolically,

$\left(\Lambda ^{k}(V)\right)\wedge \left(\Lambda ^{p}(V)\right)\subset \Lambda ^{k+p}(V).$

Moreover, the exterior product is graded anticommutative, meaning that if α ∈ Λ^k(V) and β ∈ Λ^p(V), then

$\alpha \wedge \beta =(-1)^{kp}\beta \wedge \alpha .$

In addition to studying the graded structure on the exterior algebra, Bourbaki (1989) studies additional graded structures on exterior algebras, such as those on the exterior algebra of a graded module (a module that already carries its own gradation).

Universal property

Let V be a vector space over the field K. Informally, multiplication in Λ(V) is performed by manipulating symbols and imposing a distributive law, an associative law, and using the identity v ∧ v = 0 for v ∈ V. Formally, Λ(V) is the "most general" algebra in which these rules hold for the multiplication, in the sense that any unital associative K-algebra containing V with alternating multiplication on V must contain a homomorphic image of Λ(V). In other words, the exterior algebra has the following universal property:

Given any unital associative K-algebra A and any K-linear map j : V → A such that j(v)j(v) = 0 for every v in V, then there exists precisely one unital algebra homomorphism f : Λ(V) → A such that j(v) = f(i(v)) for all v in V.

Universal property of the exterior algebra

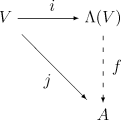
To construct the most general algebra that contains V and whose multiplication is alternating on V, it is natural to start with the most general algebra that contains V, the tensor algebra T(V), and then enforce the alternating property by taking a suitable quotient. We thus take the two-sided ideal I in T(V) generated by all elements of the form v⊗v for v in V, and define Λ(V) as the quotient

$\Lambda (V)=T(V)/I\$

(and use ∧ as the symbol for multiplication in Λ(V)). It is then straightforward to show that Λ(V) contains V and satisfies the above universal property.

As a consequence of this construction, the operation of assigning to a vector space V its exterior algebra Λ(V) is a functor from the category of vector spaces to the category of algebras.

Rather than defining Λ(V) first and then identifying the exterior powers Λ^k(V) as certain subspaces, one may alternatively define the spaces Λ^k(V) first and then combine them to form the algebra Λ(V). This approach is often used in differential geometry and is described in the next section.

Generalizations

Given a commutative ring R and an R-module M, we can define the exterior algebra Λ(M) just as above, as a suitable quotient of the tensor algebra T(M). It will satisfy the analogous universal property. Many of the properties of Λ(M) also require that M be a projective module. Where finite dimensionality is used, the properties further require that M be finitely generated and projective. Generalizations to the most common situations can be found in (Bourbaki 1989).

Exterior algebras of vector bundles are frequently considered in geometry and topology. There are no essential differences between the algebraic properties of the exterior algebra of finite-dimensional vector bundles and those of the exterior algebra of finitely generated projective modules, by the Serre–Swan theorem. More general exterior algebras can be defined for sheaves of modules.

Duality

Alternating operators

Given two vector spaces V and X, an alternating operator (or anti-symmetric operator) from V^k to X is a multilinear map

$f:V^{k}\to X$

such that whenever v₁,...,v_k are linearly dependent vectors in V, then

$f(v_{1},\ldots ,v_{k})=0$

The map

$w:V^{k}\to \Lambda ^{k}(V)$

which associates to k vectors from V their exterior product, i.e. their corresponding k-vector, is also alternating. In fact, this map is the "most general" alternating operator defined on V^k: given any other alternating operator f : V^k → X, there exists a unique linear map φ : Λ^k(V) → X with f = φ ∘ w. This universal property characterizes the space Λ^k(V) and can serve as its definition.

Alternating multilinear forms

Geometric interpretation for the exterior product of n 1-forms (ε, η, ω) to obtain an n-form ("mesh" of coordinate surfaces, here planes), for n = 1, 2, 3. The "circulations" show orientation.

The above discussion specializes to the case when X = K, the base field. In this case an alternating multilinear function

$f:V^{k}\to K\$

is called an alternating multilinear form. The set of all alternating multilinear forms is a vector space, as the sum of two such maps, or the product of such a map with a scalar, is again alternating. By the universal property of the exterior power, the space of alternating forms of degree k on V is naturally isomorphic with the dual vector space (Λ^kV)^∗. If V is finite-dimensional, then the latter is naturally isomorphic to Λ^k(V^∗). In particular, the dimension of the space of anti-symmetric maps from V^k to K is the binomial coefficient n choose k.

Under this identification, the exterior product takes a concrete form: it produces a new anti-symmetric map from two given ones. Suppose ω : V^k → K and η : V^m → K are two anti-symmetric maps. As in the case of tensor products of multilinear maps, the number of variables of their exterior product is the sum of the numbers of their variables. It is defined as follows:

$\omega \wedge \eta ={\frac {(k+m)!}{k!\,m!}}\operatorname {Alt} (\omega \otimes \eta )$

where the alternation Alt of a multilinear map is defined to be the signed average of the values over all the permutations of its variables:

$\operatorname {Alt} (\omega )(x_{1},\ldots ,x_{k})={\frac {1}{k!}}\sum _{\sigma \in S_{k}}\operatorname {sgn} (\sigma )\,\omega (x_{\sigma (1)},\ldots ,x_{\sigma (k)}).$

This definition of the exterior product is well-defined even if the field K has finite characteristic, if one considers an equivalent version of the above that does not use factorials or any constants:

${\omega \wedge \eta (x_{1},\ldots ,x_{k+m})}=\sum _{\sigma \in Sh_{k,m}}\operatorname {sgn} (\sigma )\,\omega (x_{\sigma (1)},\ldots ,x_{\sigma (k)})\eta (x_{\sigma (k+1)},\ldots ,x_{\sigma (k+m)}),$

where here Sh_k,m ⊂ S_k+m is the subset of (k,m) shuffles: permutations σ of the set {1,2,…,k + m} such that σ(1)  < σ(2) < … < σ(k), and σ(k + 1) < σ(k + 2) < … < σ(k + m).

Bialgebra structure

In formal terms, there is a correspondence between the graded dual of the graded algebra Λ(V) and alternating multilinear forms on V. The exterior product of multilinear forms defined above is dual to a coproduct defined on Λ(V), giving the structure of a coalgebra.

The coproduct is a linear function Δ : Λ(V) → Λ(V) ⊗ Λ(V) given on decomposable elements by

$\Delta (x_{1}\wedge \dots \wedge x_{k})=\sum _{p=0}^{k}\sum _{\sigma \in Sh_{p,k-p}}\operatorname {sgn} (\sigma )(x_{\sigma (1)}\wedge \dots \wedge x_{\sigma (p)})\otimes (x_{\sigma (p+1)}\wedge \dots \wedge x_{\sigma (k)}).$

For example,

$\Delta (x_{1})=1\otimes x_{1}+x_{1}\otimes 1,$

$\Delta (x_{1}\wedge x_{2})=1\otimes (x_{1}\wedge x_{2})+x_{1}\otimes x_{2}-x_{2}\otimes x_{1}+(x_{1}\wedge x_{2})\otimes 1.$

This extends by linearity to an operation defined on the whole exterior algebra. In terms of the coproduct, the exterior product on the dual space is just the graded dual of the coproduct:

$(\alpha \wedge \beta )(x_{1}\wedge \dots \wedge x_{k})=(\alpha \otimes \beta )\left(\Delta (x_{1}\wedge \dots \wedge x_{k})\right)$

where the tensor product on the right-hand side is of multilinear linear maps (extended by zero on elements of incompatible homogeneous degree: more precisely, α∧β = ε ∘ (α⊗β) ∘ Δ, where ε is the counit, as defined presently).

The counit is the homomorphism ε : Λ(V) → K which returns the 0-graded component of its argument. The coproduct and counit, along with the exterior product, define the structure of a bialgebra on the exterior algebra.

With an antipode defined on homogeneous elements by S(x) = (−1)^{deg x}x, the exterior algebra is furthermore a Hopf algebra.

Interior product

ดูเพิ่ม: Interior product

Suppose that V is finite-dimensional. If V^* denotes the dual space to the vector space V, then for each α ∈ V^*, it is possible to define an antiderivation on the algebra Λ(V),

$i_{\alpha }:\Lambda ^{k}V\rightarrow \Lambda ^{k-1}V.$

This derivation is called the interior product with α, or sometimes the insertion operator, or contraction by α.

Suppose that w ∈ Λ^kV. Then w is a multilinear mapping of V^* to K, so it is defined by its values on the k-fold Cartesian product V^* × V^* × ... × V^*. If u₁, u₂, ..., u_k−1 are k − 1 elements of V^*, then define

$(i_{\alpha }{\mathbf {w} })(u_{1},u_{2}\dots ,u_{k-1})={\mathbf {w} }(\alpha ,u_{1},u_{2},\dots ,u_{k-1}).$

Additionally, let i_αf = 0 whenever f is a pure scalar (i.e., belonging to Λ⁰V).

Axiomatic characterization and properties

The interior product satisfies the following properties:

1. For each k and each α ∈ V^*,

   $i_{\alpha }:\Lambda ^{k}V\rightarrow \Lambda ^{k-1}V.$

   (By convention, Λ⁻¹ = {0}.)

2. If v is an element of V (= Λ¹V), then i_αv = α(v) is the dual pairing between elements of V and elements of V^*.
3. For each α ∈ V^*, iα is a graded derivation of degree −1:

   $i_{\alpha }(a\wedge b)=(i_{\alpha }a)\wedge b+(-1)^{\deg a}a\wedge (i_{\alpha }b).$

In fact, these three properties are sufficient to characterize the interior product as well as define it in the general infinite-dimensional case.

Further properties of the interior product include:

• $i_{\alpha }\circ i_{\alpha }=0.$
• $i_{\alpha }\circ i_{\beta }=-i_{\beta }\circ i_{\alpha }.$

Hodge duality

บทความหลัก: Hodge dual

Suppose that V has finite dimension n. Then the interior product induces a canonical isomorphism of vector spaces

$\Lambda ^{k}(V^{*})\otimes \Lambda ^{n}(V)\to \Lambda ^{n-k}(V).\,$

In the geometrical setting, a non-zero element of the top exterior power Λⁿ(V) (which is a one-dimensional vector space) is sometimes called a volume form (or orientation form, although this term may sometimes lead to ambiguity.) Relative to a given volume form σ, the isomorphism is given explicitly by

$\alpha \in \Lambda ^{k}(V^{*})\mapsto i_{\alpha }\sigma \in \Lambda ^{n-k}(V).\,$

If, in addition to a volume form, the vector space V is equipped with an inner product identifying V with V^*, then the resulting isomorphism is called the Hodge dual (or more commonly the Hodge star operator)

$*:\Lambda ^{k}(V)\rightarrow \Lambda ^{n-k}(V).\,$

The composite of $*$ with itself maps Λ^k(V) → Λ^k(V) and is always a scalar multiple of the identity map. In most applications, the volume form is compatible with the inner product in the sense that it is an exterior product of an orthonormal basis of V. In this case,

$*\circ *:\Lambda ^{k}(V)\to \Lambda ^{k}(V)=(-1)^{k(n-k)+q}I$

where I is the identity, and the inner product has metric signature (p,q) — p plusses and q minuses.

Inner product

For V a finite-dimensional space, an inner product on V defines an isomorphism of V with V^∗, and so also an isomorphism of Λ^kV with (Λ^kV)^∗. The pairing between these two spaces also takes the form of an inner product. On decomposable k-vectors,

$\left\langle v_{1}\wedge \cdots \wedge v_{k},w_{1}\wedge \cdots \wedge w_{k}\right\rangle =\det(\langle v_{i},w_{j}\rangle ),$

the determinant of the matrix of inner products. In the special case v_i = w_i, the inner product is the square norm of the k-vector, given by the determinant of the Gramian matrix (⟨v_i, v_j⟩). This is then extended bilinearly (or sesquilinearly in the complex case) to a non-degenerate inner product on Λ^kV. If e_i, i=1,2,...,n, form an orthonormal basis of V, then the vectors of the form

$e_{i_{1}}\wedge \cdots \wedge e_{i_{k}},\quad i_{1}<\cdots <i_{k},$

constitute an orthonormal basis for Λ^k(V).

With respect to the inner product, exterior multiplication and the interior product are mutually adjoint. Specifically, for v ∈ Λ^k−1(V), w ∈ Λ^k(V), and x ∈ V,

$\langle x\wedge \mathbf {v} ,\mathbf {w} \rangle =\langle \mathbf {v} ,i_{x^{\flat }}\mathbf {w} \rangle$

where x^♭ ∈ V^* is the linear functional defined by

$x^{\flat }(y)=\langle x,y\rangle$

for all y ∈ V. This property completely characterizes the inner product on the exterior algebra.

Functoriality

Suppose that V and W are a pair of vector spaces and f : V → W is a linear transformation. Then, by the universal construction, there exists a unique homomorphism of graded algebras

$\Lambda (f):\Lambda (V)\rightarrow \Lambda (W)$

such that

$\Lambda (f)|_{\Lambda ^{1}(V)}=f:V=\Lambda ^{1}(V)\rightarrow W=\Lambda ^{1}(W).$

In particular, Λ(f) preserves homogeneous degree. The k-graded components of Λ(f) are given on decomposable elements by

$\Lambda (f)(x_{1}\wedge \dots \wedge x_{k})=f(x_{1})\wedge \dots \wedge f(x_{k}).$

Let

$\Lambda ^{k}(f)=\Lambda (f)_{\Lambda ^{k}(V)}:\Lambda ^{k}(V)\rightarrow \Lambda ^{k}(W).$

The components of the transformation Λ(k) relative to a basis of V and W is the matrix of k × k minors of f. In particular, if V = W and V is of finite dimension n, then Λⁿ(f) is a mapping of a one-dimensional vector space Λⁿ to itself, and is therefore given by a scalar: the determinant of f.

Exactness

If

$0\rightarrow U\rightarrow V\rightarrow W\rightarrow 0$

is a short exact sequence of vector spaces, then

$0\to \Lambda ^{1}(U)\wedge \Lambda (V)\to \Lambda (V)\rightarrow \Lambda (W)\rightarrow 0$

is an exact sequence of graded vector spaces as is

$0\to \Lambda (U)\to \Lambda (V).$

Direct sums

In particular, the exterior algebra of a direct sum is isomorphic to the tensor product of the exterior algebras:

$\Lambda (V\oplus W)=\Lambda (V)\otimes \Lambda (W).$

This is a graded isomorphism; i.e.,

$\Lambda ^{k}(V\oplus W)=\bigoplus _{p+q=k}\Lambda ^{p}(V)\otimes \Lambda ^{q}(W).$

Slightly more generally, if

$0\rightarrow U\rightarrow V\rightarrow W\rightarrow 0$

is a short exact sequence of vector spaces then Λ^k(V) has a filtration

$0=F^{0}\subseteq F^{1}\subseteq \dotsb \subseteq F^{k}\subseteq F^{k+1}=\Lambda ^{k}(V)$

with quotients :$F^{p+1}/F^{p}=\Lambda ^{k-p}(U)\otimes \Lambda ^{p}(W)$. In particular, if U is 1-dimensional then

$0\rightarrow U\otimes \Lambda ^{k-1}(W)\rightarrow \Lambda ^{k}(V)\rightarrow \Lambda ^{k}(W)\rightarrow 0$

is exact, and if W is 1-dimensional then

$0\rightarrow \Lambda ^{k}(U)\rightarrow \Lambda ^{k}(V)\rightarrow \Lambda ^{k-1}(U)\otimes W\rightarrow 0$

is exact.

The alternating tensor algebra

If K is a field of characteristic 0, then the exterior algebra of a vector space V can be canonically identified with the vector subspace of T(V) consisting of antisymmetric tensors. Recall that the exterior algebra is the quotient of T(V) by the ideal I generated by x ⊗ x.

Let T^r(V) be the space of homogeneous tensors of degree r. This is spanned by decomposable tensors

$v_{1}\otimes \dots \otimes v_{r},\quad v_{i}\in V.$

The antisymmetrization (or sometimes the skew-symmetrization) of a decomposable tensor is defined by

$\operatorname {Alt} (v_{1}\otimes \dots \otimes v_{r})={\frac {1}{r!}}\sum _{\sigma \in {\mathfrak {S}}_{r}}\operatorname {sgn} (\sigma )v_{\sigma (1)}\otimes \dots \otimes v_{\sigma (r)}$

where the sum is taken over the symmetric group of permutations on the symbols {1,...,r}. This extends by linearity and homogeneity to an operation, also denoted by Alt, on the full tensor algebra T(V). The image Alt(T(V)) is the alternating tensor algebra, denoted A(V). This is a vector subspace of T(V), and it inherits the structure of a graded vector space from that on T(V). It carries an associative graded product ${\widehat {\otimes }}$ defined by

$t{\widehat {\otimes }}s=\operatorname {Alt} (t\otimes s).$

Although this product differs from the tensor product, the kernel of Alt is precisely the ideal I (again, assuming that K has characteristic 0), and there is a canonical isomorphism

$A(V)\cong \Lambda (V).$

Index notation

Suppose that V has finite dimension n, and that a basis e₁, ..., e_n of V is given. then any alternating tensor t ∈ A^r(V) ⊂ T^r(V) can be written in index notation as

$t=t^{i_{1}i_{2}\dots i_{r}}\,{\mathbf {e} }_{i_{1}}\otimes {\mathbf {e} }_{i_{2}}\otimes \dots \otimes {\mathbf {e} }_{i_{r}}$

where t^{i₁ ... i_r} is completely antisymmetric in its indices.

The exterior product of two alternating tensors t and s of ranks r and p is given by

$t{\widehat {\otimes }}s={\frac {1}{(r+p)!}}\sum _{\sigma \in {\mathfrak {S}}_{r+p}}\operatorname {sgn} (\sigma )t^{i_{\sigma (1)}\dots i_{\sigma (r)}}s^{i_{\sigma (r+1)}\dots i_{\sigma (r+p)}}{\mathbf {e} }_{i_{1}}\otimes {\mathbf {e} }_{i_{2}}\otimes \dots \otimes {\mathbf {e} }_{i_{r+p}}.$

The components of this tensor are precisely the skew part of the components of the tensor product s ⊗ t, denoted by square brackets on the indices:

$(t{\widehat {\otimes }}s)^{i_{1}\dots i_{r+p}}=t^{[i_{1}\dots i_{r}}s^{i_{r+1}\dots i_{r+p}]}.$

The interior product may also be described in index notation as follows. Let $t=t^{i_{0}i_{1}\dots i_{r-1}}$ be an antisymmetric tensor of rank r. Then, for α ∈ V^*, i_αt is an alternating tensor of rank r − 1, given by

$(i_{\alpha }t)^{i_{1}\dots i_{r-1}}=r\sum _{j=0}^{n}\alpha _{j}t^{ji_{1}\dots i_{r-1}}.$

where n is the dimension of V.

Applications

Linear algebra

In applications to linear algebra, the exterior product provides an abstract algebraic manner for describing the determinant and the minors of a matrix. For instance, it is well known that the magnitude of the determinant of a square matrix is equal to the volume of the parallelotope whose sides are the columns of the matrix. This suggests that the determinant can be defined in terms of the exterior product of the column vectors. Likewise, the k×k minors of a matrix can be defined by looking at the exterior products of column vectors chosen k at a time. These ideas can be extended not just to matrices but to linear transformations as well: the magnitude of the determinant of a linear transformation is the factor by which it scales the volume of any given reference parallelotope. So the determinant of a linear transformation can be defined in terms of what the transformation does to the top exterior power. The action of a transformation on the lesser exterior powers gives a basis-independent way to talk about the minors of the transformation.

Linear geometry

The decomposable k-vectors have geometric interpretations: the bivector $u\wedge v$ represents the plane spanned by the vectors, "weighted" with a number, given by the area of the oriented parallelogram with sides u and v. Analogously, the 3-vector $u\wedge v\wedge w$ represents the spanned 3-space weighted by the volume of the oriented parallelepiped with edges u, v, and w.

Projective geometry

Decomposable k-vectors in Λ^kV correspond to weighted k-dimensional linear subspaces of V. In particular, the Grassmannian of k-dimensional subspaces of V, denoted Gr_k(V), can be naturally identified with an algebraic subvariety of the projective space P(Λ^kV). This is called the Plücker embedding.

Differential geometry

The exterior algebra has notable applications in differential geometry, where it is used to define differential forms. A differential form at a point of a differentiable manifold is an alternating multilinear form on the tangent space at the point. Equivalently, a differential form of degree k is a linear functional on the k-th exterior power of the tangent space. As a consequence, the exterior product of multilinear forms defines a natural exterior product for differential forms. Differential forms play a major role in diverse areas of differential geometry.

In particular, the exterior derivative gives the exterior algebra of differential forms on a manifold the structure of a differential algebra. The exterior derivative commutes with pullback along smooth mappings between manifolds, and it is therefore a natural differential operator. The exterior algebra of differential forms, equipped with the exterior derivative, is a cochain complex whose cohomology is called the de Rham cohomology of the underlying manifold and plays a vital role in the algebraic topology of differentiable manifolds.

Representation theory

In representation theory, the exterior algebra is one of the two fundamental Schur functors on the category of vector spaces, the other being the symmetric algebra. Together, these constructions are used to generate the irreducible representations of the general linear group; see fundamental representation.

Physics

The exterior algebra is an archetypal example of a superalgebra, which plays a fundamental role in physical theories pertaining to fermions and supersymmetry. For a physical discussion, see Grassmann number. For various other applications of related ideas to physics, see superspace and supergroup (physics).

Lie algebra homology

Let L be a Lie algebra over a field K, then it is possible to define the structure of a chain complex on the exterior algebra of L. This is a K-linear mapping

$\partial :\Lambda ^{p+1}L\to \Lambda ^{p}L$

defined on decomposable elements by

$\partial (x_{1}\wedge \cdots \wedge x_{p+1})={\frac {1}{p+1}}\sum _{j<\ell }(-1)^{j+\ell +1}[x_{j},x_{\ell }]\wedge x_{1}\wedge \cdots \wedge {\hat {x}}_{j}\wedge \cdots \wedge {\hat {x}}_{\ell }\wedge \cdots \wedge x_{p+1}.$

The Jacobi identity holds if and only if ∂∂ = 0, and so this is a necessary and sufficient condition for an anticommutative nonassociative algebra L to be a Lie algebra. Moreover, in that case ΛL is a chain complex with boundary operator ∂. The homology associated to this complex is the Lie algebra homology.

Homological algebra

The exterior algebra is the main ingredient in the construction of the Koszul complex, a fundamental object in homological algebra.

History

The exterior algebra was first introduced by Hermann Grassmann in 1844 under the blanket term of Ausdehnungslehre, or Theory of Extension. This referred more generally to an algebraic (or axiomatic) theory of extended quantities and was one of the early precursors to the modern notion of a vector space. Saint-Venant also published similar ideas of exterior calculus for which he claimed priority over Grassmann.

The algebra itself was built from a set of rules, or axioms, capturing the formal aspects of Cayley and Sylvester's theory of multivectors. It was thus a calculus, much like the propositional calculus, except focused exclusively on the task of formal reasoning in geometrical terms. In particular, this new development allowed for an axiomatic characterization of dimension, a property that had previously only been examined from the coordinate point of view.

The import of this new theory of vectors and multivectors was lost to mid 19th century mathematicians, until being thoroughly vetted by Giuseppe Peano in 1888. Peano's work also remained somewhat obscure until the turn of the century, when the subject was unified by members of the French geometry school (notably Henri Poincaré, Élie Cartan, and Gaston Darboux) who applied Grassmann's ideas to the calculus of differential forms.

A short while later, Alfred North Whitehead, borrowing from the ideas of Peano and Grassmann, introduced his universal algebra. This then paved the way for the 20th century developments of abstract algebra by placing the axiomatic notion of an algebraic system on a firm logical footing.

See also

• Symmetric algebra, the symmetric analog
• Clifford algebra, a quantum deformation of the exterior algebra by a quadratic form
• Weyl algebra, a quantum deformation of the symmetric algebra by a symplectic form
• Multilinear algebra
• Tensor algebra
• Geometric algebra
• Koszul complex

References

Mathematical references

• Bishop, R.; Goldberg, S.I. (1980), Tensor analysis on manifolds, Dover, ISBN 0-486-64039-6

Includes a treatment of alternating tensors and alternating forms, as well as a detailed discussion of Hodge duality from the perspective adopted in this article.

• Bourbaki, Nicolas (1989), Elements of mathematics, Algebra I, Springer-Verlag, ISBN 3-540-64243-9

This is the main mathematical reference for the article. It introduces the exterior algebra of a module over a commutative ring (although this article specializes primarily to the case when the ring is a field), including a discussion of the universal property, functoriality, duality, and the bialgebra structure. See chapters III.7 and III.11.

• Bryant, R.L.; Chern, S.S.; Gardner, R.B.; Goldschmidt, H.L.; Griffiths, P.A. (1991), Exterior differential systems, Springer-Verlag

This book contains applications of exterior algebras to problems in partial differential equations. Rank and related concepts are developed in the early chapters.

• Mac Lane, S.; Birkhoff, G. (1999), Algebra, AMS Chelsea, ISBN 0-8218-1646-2

Chapter XVI sections 6–10 give a more elementary account of the exterior algebra, including duality, determinants and minors, and alternating forms.

• Sternberg, Shlomo (1964), Lectures on Differential Geometry, Prentice Hall

Contains a classical treatment of the exterior algebra as alternating tensors, and applications to differential geometry.

Historical references

• Bourbaki, Nicolas (1989), "Historical note on chapters II and III", Elements of mathematics, Algebra I, Springer-Verlag
• Clifford, W. (1878), "Applications of Grassmann's Extensive Algebra", American Journal of Mathematics, The Johns Hopkins University Press, 1 (4): 350–358, doi:10.2307/2369379, JSTOR 2369379
• Forder, H. G. (1941), The Calculus of Extension, Cambridge University Press
• Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre – Ein neuer Zweig der Mathematik (The Linear Extension Theory – A new Branch of Mathematics) alternative reference
• Kannenberg, Lloyd (2000), Extension Theory (translation of Grassmann's Ausdehnungslehre), American Mathematical Society, ISBN 0-8218-2031-1
• Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva; Kannenberg, Lloyd (1999), Geometric calculus: According to the Ausdehnungslehre of H. Grassmann, Birkhäuser, ISBN 978-0-8176-4126-9.
• Whitehead, Alfred North (1898), a Treatise on Universal Algebra, with Applications, Cambridge

Other references and further reading

• Browne, J.M. (2007), Grassmann algebra – Exploring applications of Extended Vector Algebra with Mathematica, Published on line {{citation}}: แหล่งข้อมูลอื่นใน |publisher= (help)

An introduction to the exterior algebra, and geometric algebra, with a focus on applications. Also includes a history section and bibliography.

• Spivak, Michael (1965), Calculus on manifolds, Addison-Wesley, ISBN 978-0-8053-9021-6

Includes applications of the exterior algebra to differential forms, specifically focused on integration and Stokes's theorem. The notation Λ^kV in this text is used to mean the space of alternating k-forms on V; i.e., for Spivak Λ^kV is what this article would call Λ^kV*. Spivak discusses this in Addendum 4.

• Strang, G. (1993), Introduction to linear algebra, Wellesley-Cambridge Press, ISBN 978-0-9614088-5-5

Includes an elementary treatment of the axiomatization of determinants as signed areas, volumes, and higher-dimensional volumes.

• Onishchik, A.L. (2001), "Exterior algebra", ใน Hazewinkel, Michiel (บ.ก.), Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
• Wendell H. Fleming (1965) Functions of Several Variables, Addison-Wesley.

Chapter 6: Exterior algebra and differential calculus, pages 205–38. This textbook in multivariate calculus introduces the exterior algebra of differential forms adroitly into the calculus sequence for colleges.

• Winitzki, S. (2010), Linear Algebra via Exterior Products, Published on line {{citation}}: แหล่งข้อมูลอื่นใน |publisher= (help)

An introduction to the coordinate-free approach in basic finite-dimensional linear algebra, using exterior products.

• Shafarevich, I. R. (2012). Linear Algebra and Geometry. Springer. ISBN 978-3-642-30993-9. {{cite book}}: ไม่รู้จักพารามิเตอร์ |coauthors= ถูกละเว้น แนะนำ (|author=) (help)

Chapter 10: The Exterior Product and Exterior Algebras

• "The Grassmann method in projective geometry" A compilation of English translations of three notes by Cesare Burali-Forti on the application of exterior algebra to projective geometry
• C. Burali-Forti, "Introduction to Differential Geometry, following the method of H. Grassmann" An English translation of an early book on the geometric applications of exterior algebras
• "Mechanics, according to the principles of the theory of extension" An English translation of one Grassmann's papers on the applications of exterior algebra