ความสูงมาตราส่วน

ความสูงมาตราส่วนของโลกอยู่ที่ประมาณ 8.5 km ดังที่เห็นได้จากไดอะแกรมนี้ของความดันอากาศ p ที่ระดับความสูง h: ที่ระดับความสูง 0, 8.5, และ 17 กิโลเมตร ความดันอากาศอยู่ที่ประมาณ 1000, 370, และ 140 hPa ตามลำดับ

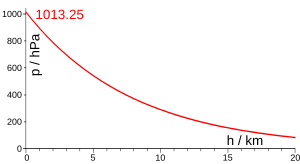
ในวิทยาศาสตร์บรรยากาศ, วิทยาศาสตร์โลก, และ วิทยาศาสตร์ดาวเคราะห์, ความสูงมาตราส่วน, ซึ่งมักแสดงด้วยตัวอักษร H, เป็นระยะทาง (ระยะทางแนวตั้ง หรือ รัศมี) ที่ ปริมาณทางกายภาพ จะลดลงด้วยปัจจัย e (ฐานของ ลอการิทึมธรรมชาติ, ซึ่งมีค่าประมาณ 2.718)

ความสูงมาตราส่วนที่ใช้ในแบบจำลองความดันบรรยากาศง่าย ๆ

สำหรับชั้นบรรยากาศของดาวเคราะห์ ความสูงมาตราส่วนคือการเพิ่มความสูงที่ทำให้ ความดันบรรยากาศ ลดลงด้วยปัจจัย e โดยความสูงมาตราส่วนจะคงที่สำหรับอุณหภูมิที่กำหนด สามารถคำนวณได้จาก

$$H={\frac {k_{\text{B}}T}{mg}}$$ หรือในรูปแบบสมการเดียวกัน $$H={\frac {RT}{Mg}}$$ โดยที่:

• k_B = ค่าคงตัวบ็อลทซ์มัน = 1.381×10⁻²³ J⋅K⁻¹‍
• R = ค่าคงที่ก๊าซ
• T = ค่าเฉลี่ยของ อุณหภูมิ บรรยากาศในหน่วย เคลวิน = 250 K สำหรับโลก
• m = มวลเฉลี่ยของโมเลกุล (หน่วยกิโลกรัม)
• M = มวลเฉลี่ยของหนึ่งโมลของอนุภาคในชั้นบรรยากาศ = 0.029 กิโลกรัม/โมล สำหรับโลก
• g = ความเร่งเนื่องจาก แรงโน้มถ่วง ณ ตำแหน่งปัจจุบัน (m/s²)

ความดัน (แรงต่อหน่วยพื้นที่) ที่ความสูงหนึ่ง ๆ เป็นผลมาจากน้ำหนักของชั้นบรรยากาศที่อยู่เหนือขึ้นไป หากที่ความสูง z ชั้นบรรยากาศมี ความหนาแน่น ρ และความดัน P การเลื่อนขึ้นไปที่ความสูง dz จะลดความดันลงเป็นจำนวน dP ซึ่งเท่ากับน้ำหนักของชั้นบรรยากาศที่มีความหนา dz

ดังนั้น: $${\frac {dP}{dz}}=-g\rho$$ โดยที่ g คือความเร่งเนื่องจากแรงโน้มถ่วง สำหรับ dz ขนาดเล็กสามารถสมมติว่า g เป็นค่าคงที่ เครื่องหมายลบหมายถึงเมื่อความสูงเพิ่มขึ้น ความดันจะลดลง ดังนั้น โดยใช้ สมการสถานะ สำหรับ ก๊าซอุดมคติ ที่มีมวลโมเลกุลเฉลี่ย M ที่อุณหภูมิ T ความหนาแน่นสามารถแสดงเป็น $$\rho ={\frac {MP}{RT}}$$

การรวมสมการเหล่านี้จะให้ผลลัพธ์เป็น $${\frac {dP}{P}}={\frac {-dz}{\frac {k_{\text{B}}T}{mg}}}$$ ซึ่งสามารถรวมกับสมการของ H ที่กำหนดไว้ข้างต้นได้ว่า: $${\frac {dP}{P}}=-{\frac {dz}{H}}$$ ซึ่งจะไม่เปลี่ยนแปลงเว้นแต่อุณหภูมิจะเปลี่ยน การรวมสมการข้างต้นและสมมติว่า P₀ คือความดันที่ความสูง z = 0 (ความดันที่ ระดับน้ำทะเล) ความดันที่ความสูง z สามารถเขียนได้ว่า: $$P=P_{0}\exp \left(-{\frac {z}{H}}\right)$$

ซึ่งแปลว่าความดันจะ ลดลงแบบเอกซ์โพเนนเชียล ตามความสูง

ใน ชั้นบรรยากาศของโลก ความดันที่ระดับน้ำทะเล P₀ มีค่าเฉลี่ยประมาณ 1.01×10⁵ Pa, มวลโมเลกุลเฉลี่ยของอากาศแห้งเท่ากับ 28.964 u ดังนั้น m = 28.964 × 1.660×10⁻²⁷ = 4.808×10⁻²⁶ kg เป็นฟังก์ชันของอุณหภูมิ ความสูงมาตราส่วนของชั้นบรรยากาศโลกคือ H/T = k/mg = (1.38/ (4.808×9.81) ) ×10³ = 29.26 m/K ซึ่งให้ผลลัพธ์เป็นความสูงมาตราส่วนต่อไปนี้สำหรับอุณหภูมิอากาศที่เป็นตัวแทน

• T = 290 K, H = 8500 m
• T = 273 K, H = 8000 m
• T = 260 K, H = 7610 m
• T = 210 K, H = 6000 m

ตัวเลขเหล่านี้ควรเปรียบเทียบกับอุณหภูมิและความหนาแน่นของชั้นบรรยากาศโลกที่พล็อตใน NRLMSISE-00 ซึ่งแสดงให้เห็นว่าความหนาแน่นของอากาศลดลงจาก 1200 g/m³ ที่ระดับน้ำทะเลเหลือ 0.5³ = 0.125 g/m³ ที่ความสูง 70 กม. ซึ่งเป็นปัจจัย 9600 บ่งชี้ความสูงมาตราส่วนเฉลี่ยที่ 70/ln (9600) = 7.64 กม. ซึ่งสอดคล้องกับค่าเฉลี่ยอุณหภูมิอากาศในช่วงนั้นที่ใกล้เคียงกับ 260 K

หมายเหตุ:

• ความหนาแน่นสัมพันธ์กับความดันตาม กฎของแก๊สอุดมคติ ดังนั้นความหนาแน่นจะลดลงแบบเอกซ์โพเนนเชียลตามความสูงจากค่า ρ₀ ที่ระดับน้ำทะเลซึ่งมีค่าประมาณ 1.2 กก./ม³
• ที่ความสูงมากกว่า 100 กม. ชั้นบรรยากาศอาจไม่ผสมผสานกันได้ดี ในกรณีนี้แต่ละสปีชีส์เคมีจะมีความสูงมาตราส่วนของตัวเอง
• ที่นี่ถือว่าอุณหภูมิและความเร่งเนื่องจากแรงโน้มถ่วงคงที่ แต่ทั้งสองค่าอาจเปลี่ยนแปลงตามระยะทางที่ไกลออกไป

ตัวอย่างของดาวเคราะห์

ความสูงมาตราส่วนโดยประมาณสำหรับดาวเคราะห์ในระบบสุริยะที่เลือก:

• ดาวศุกร์: 15.9 กม.
• โลก: 8.5 กม.
• ดาวอังคาร: 11.1 กม.
• ดาวพฤหัสบดี: 27 กม.
• ดาวเสาร์: 59.5 กม.
  • ไททัน: 21 กม.
• ดาวยูเรนัส: 27.7 กม.
• ดาวเนปจูน: 19.1–20.3 กม.
• พลูโต: ~50 กม.

ความสูงมาตราส่วนในดิสก์บาง

ภาพสเกเมติกของความสมดุลของแรงในดิสก์ก๊าซรอบวัตถุกลาง เช่น ดาวฤกษ์

สำหรับดิสก์ของก๊าซรอบวัตถุกลางที่ควบแน่น เช่น ดาวฤกษ์เริ่มต้น สามารถคำนวณระยะชั้นดิสก์ซึ่งคล้ายคลึงกับระยะชั้นของดาวเคราะห์ได้ เราเริ่มจากดิสก์ก๊าซที่มีมวลน้อยกว่าวัตถุกลางอย่างมาก เราสมมุติว่าดิสก์อยู่ในสมดุลไฮโดรสแตติกกับส่วนประกอบ z ของแรงโน้มถ่วงจากดาวฤกษ์ โดยที่แรงโน้มถ่วงจะชี้ไปที่กลางดิสก์:

$${\frac {dP}{dz}}=-{\frac {GM_{*}\rho z}{(r^{2}+z^{2})^{3/2}}}$$

โดยที่:

• G = ค่าคงที่แรงโน้มถ่วง ≈ 6.674×10⁻¹¹ m³⋅kg⁻¹⋅s⁻²‍
• r = ระยะทางเชิงรัศมีจากศูนย์กลางของดาวฤกษ์หรือวัตถุกลาง
• z = ความสูง/ระยะห่างจากกลางดิสก์ (หรือศูนย์กลางของดาวฤกษ์)
• M_* = มวลของดาวฤกษ์/วัตถุกลาง
• P = ความดันของก๊าซในดิสก์
• $\rho$ = ความหนาแน่นของมวลก๊าซในดิสก์

ในกรณีที่ถือว่าดิสก์บาง $z\ll r$ และสมการสมดุลไฮโดรสแตติกจะเป็น: $${\frac {dP}{dz}}\approx -{\frac {GM_{*}\rho z}{r^{3}}}$$

ในการคำนวณความดันของก๊าซ สามารถใช้ กฎของก๊าซอุดมคติ: $$P={\frac {\rho k_{\text{B}}T}{\bar {m}}}$$ โดยที่:

• T = อุณหภูมิของก๊าซในดิสก์ ซึ่งเป็นฟังก์ชันของ r แต่ไม่ขึ้นกับ z
• ${\bar {m}}$ = มวลโมเลกุลเฉลี่ยของก๊าซ

การใช้ กฎของก๊าซอุดมคติ และสมการสมดุลไฮโดรสแตติกจะให้: $${\frac {d\rho }{dz}}\approx -{\frac {GM_{*}{\bar {m}}\rho z}{kTr^{3}}}$$ ซึ่งมีคำตอบเป็น: $$\rho =\rho _{0}\exp \left(-\left({\frac {z}{h_{D}}}\right)^{2}\right)$$ โดยที่ $\rho _{0}$ คือความหนาแน่นของมวลก๊าซที่กลางดิสก์ที่ระยะ r จากศูนย์กลางของดาวฤกษ์ และ $h_{D}$ คือระยะชั้นของดิสก์ โดยมี:

$$h_{D}={\sqrt {\frac {2kTr^{3}}{GM_{*}{\bar {m}}}}}\approx 0.0306{\sqrt {\frac {\left(T/100\ {\text{K}}\right)\left(r/1{\text{ au}}\right)^{3}}{\left(M_{*}/M_{\odot }\right)\left({\bar {m}}/2{\text{ amu}}\right)}}}\ {\text{ au}}$$ โดยที่ $M_{\odot }$ คือ มวลดวงอาทิตย์, ${\text{au}}$ คือ หน่วยดาราศาสตร์ และ ${\text{amu}}$ คือ หน่วยมวลอะตอม

เป็นการประมาณที่ช่วยให้เห็นภาพ หากเรามองข้ามความแปรผันตามรัศมีในอุณหภูมิ $T$ เราจะเห็นว่า $h_{D}\propto r^{3/2}$ และดิสก์จะเพิ่มความสูงขึ้นเมื่อเคลื่อนที่ออกจากวัตถุกลาง

เนื่องจากสมมุติฐานว่าอุณหภูมิของก๊าซในดิสก์ T ไม่ขึ้นกับ z, $h_{D}$ บางครั้งเรียกว่า ระยะชั้นของดิสก์ที่มีอุณหภูมิคงที่

ระยะชั้นดิสก์ในสนามแม่เหล็ก

สนามแม่เหล็กในดิสก์ก๊าซบางรอบวัตถุกลางสามารถเปลี่ยนแปลงระยะชั้นของดิสก์ได้ ตัวอย่างเช่น หากดิสก์ที่ไม่เป็นตัวนำไฟฟ้าอย่างสมบูรณ์หมุนผ่านสนามแม่เหล็กพอลอยดอล (เช่น สนามแม่เหล็กเริ่มต้นตั้งฉากกับระนาบของดิสก์) จะมีการผลิตสนามแม่เหล็กโทริคัล (เช่น ขนานกับระนาบดิสก์) ภายในดิสก์ ซึ่งจะทำให้ดิสก์ถูก "หนีบ" และบีบอัด ในกรณีนี้ ความหนาแน่นของก๊าซในดิสก์คือ

$$\rho (r,z)=\rho _{0}(r)\exp \left(-\left({\frac {z}{h_{D}}}\right)^{2}\right)-\rho _{\text{cut}}(r)\left[1-\exp \left(-\left({\frac {z}{h_{D}}}\right)^{2}\right)\right]$$ โดยที่ความหนาแน่น "ตัดขาด" $\rho _{\text{cut}}$ มีรูปแบบเป็น: $$\rho _{\rm {cut}}(r)=(\mu _{0}\sigma _{D}r)^{2}\left({\frac {B_{z}^{2}}{\mu _{0}}}\right)\left({\frac {\Omega _{*}}{\Omega _{K}}}-1\right)^{2}$$ โดยที่:

• $\mu _{0}$ คือ ความสามารถในการนำของสุญญากาศ
• $\sigma _{D}$ คือ ความสามารถในการนำไฟฟ้าของดิสก์
• $B_{z}$ คือ ความหนาแน่นของฟลักซ์แม่เหล็กของสนามพอลอยดอลในทิศทาง $z$
• $\Omega _{*}$ คือ ความเร็วเชิงมุมการหมุนของวัตถุกลาง (หากสนามแม่เหล็กพอลอยดอลไม่ขึ้นกับวัตถุกลาง $\Omega _{*}$ สามารถตั้งเป็นศูนย์ได้)
• $\Omega _{K}$ คือ ความเร็วเชิงมุมเคปเลอเรียนของดิสก์ที่ระยะ $r$ จากวัตถุกลาง

สูตรเหล่านี้ให้ความสูงสูงสุดของดิสก์ที่มีแม่เหล็ก $H_{B}$ เป็น: $$H_{B}=h_{D}{\sqrt {\ln \left(1+\rho _{0}/\rho _{\rm {cut}}\right)}},$$ ในขณะที่ระยะชั้นแม่เหล็ก e-folding $h_{B}$ คือ: $$h_{B}=h_{D}{\sqrt {\ln \left(1+{\frac {1-1/e}{1/e+\rho _{\text{cut}}/\rho _{0}}}\right)}}\ .$$