ออร์บิทัลเชิงอะตอม

ในทฤษฎีอะตอมและกลศาสตร์ควอนตัม ออร์บิทัลเชิงอะตอม (Atomic orbitals) เป็นฟังก์ชันที่สามารถอธิบายตำแหน่งและพฤติกรรมคล้ายคลื่นของอิเล็กตรอนในอะตอม ฟังก์ชันนี้สามารถใช้ในการคำนวณความน่าจะเป็นที่จะพบอิเล็กตรอนใดๆ ของอะตอมในบริเวณรอบนิวเคลียสของอะตอม คำว่าออร์บิทัลเชิงอะตอมยังอาจหมายถึงบริเวณหรือช่องว่างทางกายภาพที่สามารถคำนวณได้ว่าอิเล็กตรอนมีอยู่ ตามที่คำนวณไว้โดยรูปแบบทางคณิตศาสตร์เฉพาะของออร์บิทัล
แต่ละออร์บิทัลในอะตอมมีลักษณะเฉพาะด้วยชุดค่าของเลขควอนตัมสามชุด คือ n ℓ และ mℓ ซึ่งสอดคล้องกับพลังงานของอิเล็กตรอนและโมเมนตัมเชิงมุมตามลำดับ แทนที่จะใช้เลขควอนตัมแม่เหล็ก ออร์บิทัลมักถูกระบุด้วยพหุนามฮาร์โมนิก (เช่น xy, x2 − y2) และแต่ละออร์บิทัลสามารถบรรจุอิเล็กตรอนได้สูงสุดสองตัว โดยแต่ละตัวจะมีเลขควอนตัมของสปินเป็นค่าเฉพาะ ส่วนสัญลักษณ์ s orbital, p orbital, d orbital, และ f orbital แสดงถึงออร์บิทัลซึ่งขึ้นอยู่กับเลขควอนตัมโมเมนตัมเชิงมุม ℓ = 0, 1, 2, และ 3 ตามลำดับ. ชื่อเหล่านี้พร้อมกับค่าของ n, aใช้เพื่ออธิบายโครงร่างอิเล็กตรอนของอะตอม พวกมันได้มาจากคำอธิบายโดยนักสเปกโทรสโกปีในยุคแรกๆ ของเส้นสเปกโทรสโกปีของโลหะอัลคาไลบางชุดว่ามีความ sharp, principal, diffuse และ fundamental. ออร์บิทัลที่มีค่า ℓ > 3 จะใช้เป็นตัวอักษรที่ต่อเนื่องจาก f ไปเรื่อย ๆ (g, h, i, k, ...), โดยละเว้น j เนื่องจากบางภาษาไม่แยกความแตกต่างระหว่างตัวอักษร "i" และ "j"
ออร์บิทัลเชิงอะตอมเป็นองค์ประกอบพื้นฐานของแบบจำลองของอะตอมเชิงออร์บิทัล (กลุ่มหมอกอิเล็กตรอนหรือแบบจำลองกลศาสตร์ของคลื่น) ซึ่งเป็นวิธีคิดที่ทันสมัยสำหรับการแสดงพฤติกรรมของอิเล็กตรอนในสสาร ในแบบจำลองนี้ กลุ่มหมอกอิเล็กตรอนของอะตอมอาจถูกมองว่าสร้างขึ้นจากการจัดเรียงอิเล็กตรอนที่เป็นผลมาจากออร์บิทัลของอะตอม ส่วนคาบซ้ำของหมู่ธาตุ 2, 6, 10 และ 14 ภายในตารางธาตุเกิดขึ้นจากจำนวนอิเล็กตรอนทั้งหมดที่บรรจุเต็มในออร์บิทัล s, p, d และ f ตามลำดับ พลังงานของออร์บิทัลบางชนิดจะใกล้เคียงกันมาก ดังนั้นลำดับในการเติมอิเล็กตรอนในออร์บิทัล ไม่ขึ้นอยู่กับเลขควอมตัม n (เช่น Cr = [Ar] 4s1 3d5 และ Cr2+ = [Ar] 3d4) ที่มีการเติมอิเล็กตรอนใน 4s ก่อน 3d แต่เมื่ออะตอมมีประจุบวก จะดึงอิเล็กตรอนออกจาก 4s ก่อน เนื่องจากอยู่ในระดับชั้นพลังงานที่สูงกว่า

คุณสมบัติของอิเล็กตรอน[แก้]
ด้วยการพัฒนากลศาสตร์ควอนตัมและการค้นพบจากการทดลอง (เช่น การเลี้ยวเบนของอิเล็กตรอนแบบสลิตสองช่อง) พบว่าอิเล็กตรอนที่โคจรรอบนิวเคลียสไม่สามารถอธิบายได้แน่ชัดว่าเป็นอนุภาค แต่จำเป็นต้องอธิบายด้วยทวิภาคของคลื่น–อนุภาค ซึ่งอธิบายได้ดังนี้
คุณสมบัติคล้ายคลื่น:
- อิเล็กตรอนไม่ได้โคจรรอบนิวเคลียสในลักษณะของดาวเคราะห์ที่โคจรรอบดวงอาทิตย์ แต่มีอยู่ในรูปของคลื่นนิ่ง ดังนั้นพลังงานที่ต่ำที่สุดเท่าที่จะเป็นไปได้ที่อิเล็กตรอนสามารถรับได้จะคล้ายกับความถี่มูลฐานของคลื่นบนเส้นเชือก ส่วนสถานะพลังงานที่สูงขึ้นจะเป็นลักษณะฮาร์มอนิกของความถี่มูลฐานนั้น
- อิเล็กตรอนไม่อยู่ในตำแหน่งที่แน่นอน แม้ว่าความน่าจะเป็นจากอิเล็กตรอนเพียงหนึ่งตัวสามารถพบได้จากฟังก์ชันคลื่นของอิเล็กตรอน แต่ประจุของอิเล็กตรอนจะถูกกระจายออกไปในโดยกระจายอย่างต่อเนื่อง เป็นสัดส่วน ณ จุดใดๆ เทียบกับขนาดกำลังสองของฟังก์ชันคลื่นของอิเล็กตรอน
คุณสมบัติคล้ายอนุภาค:
- จำนวนอิเล็กตรอนที่โคจรรอบนิวเคลียสสามารถเป็นจำนวนเต็มได้เท่านั้น
- อิเล็กตรอนสามารถเคลื่อนที่ระหว่างระดับชั้นพลังงานเหมือนอนุภาค ตัวอย่างเช่น ถ้าโฟตอนหนึ่งตัวกระทบกับอิเล็กตรอน ผลที่ตามมาคืออิเล็กตรอนเพียงตัวเดียวจะเปลี่ยนเป็นสถานะกระตุ้น
- อิเล็กตรอนยังคงคุณสมบัติคล้ายอนุภาค เช่น แต่ละสถานะของคลื่นมีประจุไฟฟ้าเท่ากับอิเล็กตรอน แต่ละสถานะของคลื่นจะมีการหมุนแบบไม่ต่อเนื่องเพียงครั้งเดียว (หมุนขึ้นหรือหมุนลง) ซึ่งขึ้นอยู่กับการซ้อนทับของควอนตัม
ดังนั้น อิเล็กตรอนจึงไม่สามารถอธิบายง่ายๆ ได้ว่าเป็นอนุภาค แต่อาจเป็นกลุ่มหมอกขนาดใหญ่และมักมีรูปร่างแปลกประหลาด กระจายอยู่รอบๆ นิวเคลียส ออร์บิทัลเชิงอะตอมจะอธิบายรูปร่างของกลุ่มหมอกนี้ได้ก็ต่อเมื่อมีอิเล็กตรอนอยู่ตัวเดียว เมื่อมีการเพิ่มอิเล็กตรอนมากขึ้น อิเล็กตรอนเพิ่มเติมมีแนวโน้มที่จะเติมเต็มปริมาตรของพื้นที่รอบนิวเคลียสให้เท่าๆ กันมากขึ้น เพื่อให้กลุ่มหมอกที่ได้มีแนวโน้มไปทางทรงกลม จากหลักความไม่แน่นอนที่ใช้อธิบายตำแหน่งของอิเล็กตรอนได้
คำนิยามควอนตัมเชิงกลอย่างเป็นทางการ[แก้]
ออร์บิทัลของอะตอมอาจกำหนดได้แม่นยำกว่าในภาษาควอนตัมเชิงกลที่เป็นทางการ ซึ่งเป็นคำตอบโดยประมาณของสมการชโรดิงเงอร์สำหรับอิเล็กตรอนที่จับกับอะตอมด้วยสนามไฟฟ้าของนิวเคลียสในอะตอม โดยเฉพาะอย่างยิ่ง ในกลศาสตร์ควอนตัม สถานะของอะตอมจะถูกประมาณจากชุดค่าผสมเชิงเส้นของผลเฉลยจากหนึ่งฟังก์ชันของอิเล็กตรอน ส่วนประกอบเชิงพื้นที่ของฟังก์ชันอิเล็กตรอนเดี่ยวเหล่านี้เรียกว่าออร์บิทัลของอะตอม (เมื่อพิจารณาส่วนประกอบของสปินด้วย จะสามารถอธิบายได้ถึงวงโคจรของอะตอม) ดังนั้นการเคลื่อนที่ของอิเล็กตรอนจึงสัมพันธ์กัน แต่มักจะประมาณโดยแบบจำลองอนุภาคอิสระของผลเฉลยของฟังก์ชันคลื่นอิเล็กตรอน (ตัวอย่างเช่น แรงกระจายของลอนดอน ขึ้นอยู่กับความสัมพันธ์ของการเคลื่อนที่ของอิเล็กตรอน)
ในฟิสิกส์อะตอม เส้นสเปกตรัมของอะตอมสอดคล้องกับการเปลี่ยนผ่านระหว่างสถานะควอนตัมของอะตอม สถานะเหล่านี้ถูกระบุด้วยชุดของเลขควอนตัมที่สรุปไว้ในสัญลักษณ์ของคำศัพท์ และมักจะเกี่ยวข้องกับการกำหนดค่าอิเล็กตรอนเฉพาะ (เช่น 1s2 2s2 2p6 สำหรับสถานะพื้นของสัญลักษณ์นีออน: 1S0) .
สัญกรณ์นี้หมายความว่าสเลเตอร์ดีเทอร์มิแนนต์ที่สอดคล้องกันนั้นมีน้ำหนักที่สูงกว่าใน configuration interaction expansion แนวคิดเกี่ยวกับวงโคจรของอะตอมจึงเป็นแนวคิดหลักในการแสดงภาพกระบวนการกระตุ้นที่เกี่ยวข้องกับการเปลี่ยนแปลงที่กำหนด ตัวอย่างเช่น เราสามารถบอกได้ว่าการเปลี่ยนผ่านเฉพาะนั้นสอดคล้องกับการกระตุ้นของอิเล็กตรอนจากออร์บิทัลที่มีอิเล็กตรอนไปยังอีกออร์บิทัลหนึ่งที่ว่างอยู่ แต่สิ่งสำคัญคือต้องจำไว้ว่าอิเล็กตรอนเป็นเฟอร์มิออนและอยู่ภายใต้หลักการกีดกันของเพาลี อิเล็กตรอนจึงไม่สามารถแยกความแตกต่างจากกันได้ ยิ่งกว่านั้น บางครั้งมันเกิดขึ้นที่ configuration interaction expansion เกิดช้ามากและเราไม่สามารถพูดถึงฟังก์ชันคลื่นเพียงหนึ่งตัวได้ เพราะมันเป็นความสัมพันธ์ของอิเล็กตรอนที่มีขนาดใหญ่
โดยพื้นฐานแล้ว ออร์บิทัลเชิงอะตอมเป็นฟังก์ชันคลื่นที่มีอิเล็กตรอนหนึ่งตัว แม้ว่าอะตอมส่วนใหญ่มีอิเล็กตรอนหลายตัว ดังนั้นมุมมองของอิเล็กตรอนหนึ่งตัวจึงเป็นค่าประมาณ และเมื่อนึกถึงออร์บิทัล ส่วนใหญ่เราจะได้รับข้อมูลจากการประมาณแบบฮาร์ทรี-ฟ็อก ซึ่งเป็นวิธีหนึ่งที่ช่วยลดความซับซ้อนของทฤษฎีออร์บิทัลเชิงโมเลกุล
ชนิดของออร์บิทัล[แก้]
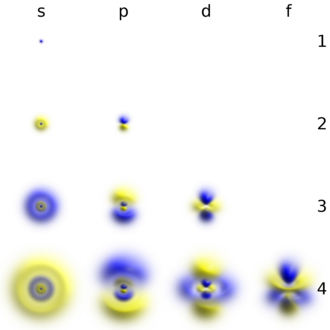
ออร์บิทัลเชิงอะตอมเป็นออร์บิทัลคล้ายไฮโดรเจน (The hydrogen-like orbitals) ซึ่งเป็นคำตอบที่ถูกต้องของสมการชโรดิงเงอร์สำหรับอะตอมที่คล้ายไฮโดรเจน (เช่น อะตอมที่มีอิเล็กตรอน 1 ตัว) อีกทางหนึ่ง ออร์บิทัลของอะตอมหมายถึงฟังก์ชันที่ขึ้นอยู่กับพิกัดของอิเล็กตรอนหนึ่งตัว แต่ใช้เป็นจุดเริ่มต้นสำหรับการประมาณฟังก์ชันคลื่นที่ขึ้นอยู่กับ simultaneous coordinates ของอิเล็กตรอนทั้งหมดในอะตอมหรือโมเลกุล ระบบพิกัดที่เลือกสำหรับออร์บิทัลมักจะเป็นระบบพิกัดเชิงขั้ว (r, θ, φ) ในอะตอม และระบบพิกัดคาร์ทีเซียน (x, y, z) ในโมเลกุลที่มีหลายอะตอม ข้อได้เปรียบของพิกัดเชิงขั้วในที่นี้คือฟังก์ชันคลื่นโคจรเป็นผลคูณของสามตัวแปรที่แต่ละส่วนขึ้นอยู่กับพิกัดเดียว: ψ(r, θ, φ) = R(r) Θ(θ) Φ(φ) ส่วนเชิงมุมของออร์บิทัลเชิงอะตอม Θ(θ) Φ(φ) สามารถบอกรูปร่างออร์บิทัลได้ และทำหน้าที่เป็นหนึ่งในชุดตัวแปรของฮาร์มอนิกทรงกลม Yℓm(θ, φ) (โดยที่ ℓ และ m เป็นเลขควอนตัม) และสำหรับส่วนเชิงรัศมี R(r) สามารถบอกขนาดออร์บิทัลได้ และเป็นจุดเริ่มต้นสำหรับการคำนวณคุณสมบัติของอะตอมและโมเลกุลที่มีอิเล็กตรอนจำนวนมากได้:
- ออร์บิทัลคล้ายไฮโดรเจนได้มาจากผลเฉลยของสมการชโรดิงเงอร์สำหรับอิเล็กตรอน 1 ตัวและนิวเคลียสสำหรับอะตอมคล้ายไฮโดรเจน ส่วนของฟังก์ชันที่ขึ้นอยู่กับระยะทาง r จากนิวเคลียสจะมี radial node และสลายเป็น
- ออร์บิทัลชนิดสเลเตอร์ (The Slater-type orbital: STO) เป็นรูปแบบที่ไม่มี radial node แต่แยกตัวออกจากนิวเคลียส เช่นเดียวกับออร์บิทัลที่มีลักษณะคล้ายไฮโดรเจน
- รูปแบบของออร์บิทัลแบบเกาส์เซียน (Gaussians) ไม่มีโหนดในแนวรัศมีและแยกออกเป็น
แม้ว่าออร์บิทัลคล้ายไฮโดรเจนยังคงใช้เป็นเครื่องมือในการสอน แต่การกำเนิดของคอมพิวเตอร์ทำให้ STO เป็นที่นิยมมากกว่าสำหรับอะตอมและโมเลกุลไดอะตอมมิก เนื่องจากการรวมกันของ STO สามารถแทนที่โหนดในออร์บิทัลคล้ายไฮโดรเจนได้ Gaussians มักใช้ในโมเลกุลที่มีอะตอมตั้งแต่สามอะตอมขึ้นไป แม้ว่าตัวเองจะไม่แม่นยำเท่า STO แต่การรวมกันของเกาส์เซียนจำนวนมากสามารถบรรลุความแม่นยำของออร์บิทัลคล้ายไฮโดรเจนได้
อ้างอิง[แก้]
- McCaw, Charles S. (2015). Orbitals: With Applications in Atomic Spectra (ภาษาอังกฤษ). Singapore: World Scientific Publishing Company. ISBN 9781783264162.
- Tipler, Paul; Llewellyn, Ralph (2003). Modern Physics (4 ed.). New York: W. H. Freeman and Company. ISBN 978-0-7167-4345-3.
- Griffiths, David (2000). Introduction to Quantum Mechanics (2 ed.). Benjamin Cummings. ISBN 978-0-13-111892-8.
- Cohen, Irwin; Bustard, Thomas (1966). "Atomic Orbitals: Limitations and Variations". J. Chem. Educ. 43 (4): 187. Bibcode:1966JChEd..43..187C. doi:10.1021/ed043p187.



