สลิเทอร์ลิงก์


สลิเทอร์ลิงก์ (Slitherlink) เป็นปริศนาตรรกะอย่างหนึ่ง คิดค้นโดย นิโคะริ (Nikoli) ผู้ผลิตนิตยสารปริศนาของประเทศญี่ปุ่น ตีพิมพ์ครั้งแรกในนิตยสาร Puzzle Communication Nikoli เล่มที่ 26 ประจำเดือนมิถุนายน พ.ศ. 2532
สำหรับชื่ออื่นๆ ที่เป็นที่รู้จักในต่างประเทศได้แก่ Fences, Takegaki, Loop the Loop, Ouroboros และ Dotty Dilemma ส่วนในประเทศไทย นิตยสารในเครือ ปริศนา ของบริษัท สำนักพิมพ์อาทร จำกัด ได้เรียกชื่อเกมนี้ว่า ปริศนาผนังสร้างอาณาเขต
ฮัดสัน (Hudson) เป็นผู้นำปริศนานี้ไปสร้างเป็นเกมบนเครื่องนินเทนโด ดีเอส ซึ่งใช้หน้าจอระบบสัมผัส ในชื่อ Puzzle Series Vol. 5: Slitherlink
ลักษณะและกติกา
[แก้]สลิเทอร์ลิงก์เป็นปริศนาที่เล่นบนจุดที่เรียงแถวต่อกันคล้ายตาราง ในช่องสี่เหลี่ยมจัตุรัสระหว่างจุดบางช่องมีตัวเลขกำกับอยู่ (ในยุคแรกๆ มีตัวเลขกำกับทุกช่อง) จุดประสงค์ของปริศนานี้คือให้ลากเส้นตรงเชื่อมต่อระหว่างจุดในแนวตั้งและแนวนอนให้ได้เป็นรูปปิดรูปหนึ่ง (เพียงรูปเดียว ไม่มีหลายรูป) ห้ามลากแนวทแยง เชื่อมกัน หรือตัดกัน โดยช่องที่มีตัวเลขจะหมายถึงจำนวนเส้นที่ต้องล้อมรอบช่องนั้น เช่น "2" หมายความว่าจะต้องมีเส้นที่ล้อมรอบช่องนี้สองเส้น รูปปิดที่ได้จะมีรูปแบบเดียวเท่านั้นเป็นผลเฉลย ไม่มีหลายรูปแบบ
เทคนิคการไขปริศนา
[แก้]เมื่อใดก็ตามที่จำนวนเส้นรอบช่องสี่เหลี่ยม มีเส้นล้อมรอบครบตามจำนวนที่ระบุไว้ในช่อง ช่องว่างที่เหลือสามารถทำเครื่องหมายเล็กๆ เช่นกากบาท เพื่อบ่งบอกว่าจะไม่มีเส้นอื่นผ่านทางนี้อีก อย่างไรก็ตาม วิธีของการลากเส้นล้อมรอบช่องหนึ่งๆ อาจมีได้หลายวิธี มีเพียงบางกรณีที่สามารถระบุลงไปได้ว่ามีกรณีเดียวโดยพิจารณาจากเส้นหรือตัวเลขที่อยู่ข้างเคียงประกอบ ซึ่งสามารถแจกแจงได้ดังนี้
- ช่องเลข "0" – ทั้งสี่ด้านของช่องนี้สามารถกากบาททิ้งไปได้ทันที เนื่องจากจะไม่มีเส้นใดที่ลากผ่านช่องนี้
- ช่องเลข "1" ที่มุม – สองด้านที่ชิดมุมปริศนาสามารถกากบาททิ้งไปได้ เนื่องจากเส้นที่ลากเข้าไปจะต้องลากออกมาอีกทางหนึ่ง ซึ่งทำให้จำนวนเส้นที่ล้อมรอบช่องนั้นเป็นสองเส้น ไม่ใช่หนึ่งเส้น ดังรูปที่ 1
- ช่องเลข "3" สองช่องที่ติดกันในแนวตั้งหรือแนวนอน – สำหรับกรณีนี้จะมีเส้นตรงที่ล้อมรอบทั้งสองช่องเป็นรูปตัว S หรือ Z เพียงสองกรณี ดังนั้นเราสามารถบอกได้ว่าจะมีเส้นตรงสามเส้นที่ลากผ่านส่วนบน ส่วนกลาง และส่วนล่างเสมอ (หรือส่วนซ้าย กลาง ขวา) นอกจากนั้นทั้งสองข้างของส่วนกลางจะไม่สามารถลากเส้นอื่นต่อไปได้ สามารถใส่กากบาทลงไปได้เลย ดังรูปที่ 2
- ช่องเลข "3" สองช่องที่ติดกันในแนวทแยง – ความเป็นได้ของการลากเส้นผ่านมีได้สี่กรณีคือ รูปตัว S, Z, E, 3 อย่างไรก็ตามที่ขอบด้านนอกของเลข "3" จะต้องมีเส้นลากผ่านเสมอทุกกรณี ดังรูปที่ 3
- ช่องเลข "3" สองช่องที่เรียงกันโดยมีช่องเลข "2" คั่นกลางในแนวทแยง – คล้ายกับกรณีก่อนหน้า คือจะต้องมีขอบด้านนอกของเลข "3" เสมอ ไม่ว่าจะมีเลข "2" มาคั่นกลางกี่ตัวก็ตาม (ต้องเป็นเลข "2" ล้วนเท่านั้น)
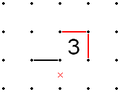
- เส้นที่เชื่อมเข้ามายังช่องเลข "3" – ด้านที่อยู่ตรงข้ามกับจุดที่เชื่อมจะต้องมีเส้นเสมอ เนื่องจากด้านที่ไม่มีเส้นของช่องเลข "3" จะต้องอยู่ติดกับจุดที่เชื่อมทางใดทางหนึ่งโดยมีความเป็นไปได้เพียงสองกรณี ดังรูปที่ 4
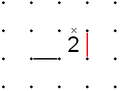
- เส้นที่เชื่อมเข้ามายังช่องเลข "2" และมีด้านตรงข้ามด้านหนึ่งเป็นกากบาท – ด้านตรงข้ามที่เหลืออีกด้านจะต้องเป็นเส้นตรงเสมอ ดังรูปที่ 5
- เส้นที่เชื่อมเข้ามายังช่องเลข "1" และมีกากบาทที่จุดเชื่อม – เส้นที่ลากเข้ามาจะเลี้ยวไปทางอื่นไม่ได้ จำเป็นต้องลากเข้ามายังช่องเลข "1" เพียงด้านเดียว ดังนั้นเส้นตรงจะไม่ถูกลากผ่านด้านตรงข้ามอย่างแน่นอน ดังรูปที่ 6
-
ช่องเลข "1" ที่มุม
-
ช่องเลข "3" สองช่องที่ติดกันในแนวตั้งหรือแนวนอน
-
ช่องเลข "3" สองช่องที่ติดกันในแนวทแยง
-
เส้นที่เชื่อมเข้ามายังช่องเลข "3"
-
เส้นที่เชื่อมเข้ามายังช่องเลข "2" และมีด้านตรงข้ามด้านหนึ่งเป็นกากบาท
แหล่งข้อมูลอื่น
[แก้]- Nikoli's English page on Slitherlink เก็บถาวร 2006-09-08 ที่ เวย์แบ็กแมชชีน
- On the NP-completeness of the Slitherlink Puzzle เก็บถาวร 2013-01-20 ที่ เวย์แบ็กแมชชีน - Slitherlink is NP-complete
- Eurogamer review of Slitherlink on the Nintendo DS เก็บถาวร 2007-09-30 ที่ เวย์แบ็กแมชชีน
- Puzzles in Southwest Airlines magazine เก็บถาวร 2007-11-17 ที่ เวย์แบ็กแมชชีน