มัชฌิมพีทาโกรัส

บทสร้างเรขาคณิตของมัชฌิมกําลังสอง และมัชฌิมพีทาโกรัส (ของตัวเลขสองจำนวน a และ b) มัชฌิมฮาร์มอนิกแสดงโดย   H, มัชฌิมเรขาคณิตโดย   G, มัชฌิมเลขคณิตโดย   A และมัชฌิมกําลังสอง (หรือรากที่สองของค่าเฉลี่ย) แสดงโดย   Q

ในคณิตศาสตร์ สามชนิดดั้งเดิมของมัชฌิมพีทาโกรัส (อังกฤษ: Pythagorean means) คือ มัชฌิมเลขคณิต (AM) มัชฌิมเรขาคณิต (GM) และมัชฌิมฮาร์มอนิก (HM) มัชฌิมเหล่านี้ถูกศึกษาโดยชาวพีทาโกรัส และนักคณิตศาสตร์ชาวกรีกรุ่นหลัง เพราะความสำคัญในเรขาคณิต และดนตรี

นิยาม

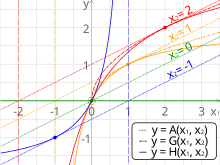การเปรียบเทียบมัชฌิมเลขคณิต เรขาคณิต และฮาร์มอนิกของตัวเลขคู่หนึ่ง เส้นประแนวตั้งเป็นมัชฌิมฮาร์มอนิก

${\begin{aligned}\operatorname {AM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\frac {1}{n}}\left(x_{1}+\;\cdots \;+x_{n}\right)\\[9pt]\operatorname {GM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\sqrt[{n}]{\left\vert x_{1}\times \,\cdots \,\times x_{n}\right\vert }}\\[9pt]\operatorname {HM} \left(x_{1},\;\ldots ,\;x_{n}\right)&={\frac {n}{\displaystyle {\frac {1}{x_{1}}}+\;\cdots \;+{\frac {1}{x_{n}}}}}\end{aligned}}$

สมบัติ

มัชฌิม $\operatorname {M}$ แต่ละตัวมีสมบัติดังนี้

การแจกแจง

$\operatorname {M} (bx_{1},\,\ldots ,\,bx_{n})=b\operatorname {M} (x_{1},\,\ldots ,\,x_{n})$

การสลับที่

$\operatorname {M} (\ldots ,\,x_{i},\,\ldots ,\,x_{j},\,\ldots )=\operatorname {M} (\ldots ,\,x_{j},\,\ldots ,\,x_{i},\,\ldots )$

สำรับทุก $i$ และ $j$

ความโมโนโทนิค

$a<b\rightarrow \operatorname {M} (a,x_{1},x_{2},\ldots x_{n})<\operatorname {M} (b,x_{1},x_{2},\ldots x_{n})$

นิจพล

$\forall x,\;\operatorname {M} (x,x,\ldots x)=x$

ความโมโนโทนิค และนิจพลบอกว่ามัชฌิมของเซตจะอยู่ระหว่างค่าน้อยสุด และค่ามากสุด

$\min(x_{1},\,\ldots ,\,x_{n})\leq \operatorname {M} (x_{1},\,\ldots ,\,x_{n})\leq \max(x_{1},\,\ldots ,\,x_{n})$

มัชฌิมฮาร์มอนิก และมัชฌิมเลขคณิตเป็นส่วนกลับของกันและกัน

$\operatorname {HM} \left({\frac {1}{x_{1}}},\,\ldots ,\,{\frac {1}{x_{n}}}\right)={\frac {1}{\operatorname {AM} \left(x_{1},\,\ldots ,\,x_{n}\right)}}$

มัชฌิมเรขาคณิตเป็นส่วนกลับของตัวเอง

$\operatorname {GM} \left({\frac {1}{x_{1}}},\,\ldots ,\,{\frac {1}{x_{n}}}\right)={\frac {1}{\operatorname {GM} \left(x_{1},\,\ldots ,\,x_{n}\right)}}$

ความไม่สมมูลระหว่างมัชฌิม

การพิสูจน์ด้วยรูปภาพ (proof without words) ทางเรขาคณิตโดย max (a,b) > มัชฌิมกำลังสอง (RMS) หรือ quadratic mean (QM) > มัชฌิมเลขคณิต (AM) > มัชฌิมเรขาคณิต (GM) > มัชฌิมฮาร์มอนิก (HM) > min (a,b) ของตัวเลขบวกสองจำนวน a และ b

หากค่า $x_{i}$ ทั้งหมดเป็นบวก การเรียงลำดับของมัชฌิมเหล่านี้คือ

$\min \leq \operatorname {HM} \leq \operatorname {GM} \leq \operatorname {AM} \leq \max$

ที่มีความสมมูลกันก็ต่อเมื่อ $x_{i}$ เท่ากันทั้งหมด

นี่คือลักษณะทั่วไปของความไม่สมมูลกันของมัชฌิมเลขคณิตและมัชฌิมเรขาคณิต และกรณีพิเศษของความไม่สมมูลกันสำหรับมัชฌิมทั่วไป หลักฐานดังต่อไปนี้จากความไม่สมมูลกันของมัชฌิมเลขคณิต-เรขาคณิต $\operatorname {AM} \leq \max$ และความเป็นคู่ส่วนกลับ ($\min$ และ $\max$ ก็เป็นส่วนกลับซึ่งกันและกันด้วย)

การศึกษาวิธีพีทาโกรัสมีความสัมพันธ์อย่างใกล้ชิดกับการศึกษาฟังก์ชัน majorization และ Schur-convex มัชฌิมฮาร์มอนิกและเรขาคณิตเป็นฟังก์ชันสมมาตรเว้าของอาร์กิวเมนต์ด้วยเหตุนี้จึงเป็นฟังก์ชัน Schur-concave ขณะที่มัชฌิมเลขคณิตเป็นฟังก์ชันเชิงเส้นของอาร์กิวเมนต์ ดังนั้นจึงเป็นทั้งฟังก์ชันสมมาตรเว้าและนูน

ดูเพิ่ม

• ค่าเฉลี่ย
• อัตราส่วนทอง

แหล่งข้อมูลอื่น

• Cantrell, David W. "Pythagorean Means". MathWorld.