ทฤษฎีบทสี่สี

ทฤษฎีบทสี่สี (อังกฤษ: Four color theorem) กล่าวว่า แผนที่ทางภูมิศาสตร์สามารถระบายด้วยสี 4 สี ซึ่งไม่มีพื้นที่ที่อยู่ติดกันมีสีเดียวกันได้เสมอ เราเรียกพื้นที่ว่าติดกันก็ต่อเมื่อมันมีส่วนของขอบร่วมกัน ไม่ใช่แค่จุดร่วมกัน และพื้นที่แต่ละชิ้นจะต้องติดเป็นอันหนึ่งอันเดียวกัน ไม่ใช่แยกเป็นหลายๆ ส่วน อย่างมิชิแกน หรืออาเซอร์ไบจาน
เป็นที่ประจักษ์ว่าสี 3 สีนั้นไม่เพียงพอ ซึ่งพิสูจน์ได้ไม่ยาก นอกจากนั้น เราสามารถพิสูจน์ได้ว่าสี 5 สีนั้นเพียงพอในการระบายแผนที่
ทฤษฎีบทสี่สี เป็นทฤษฎีบทแรกที่ถูกพิสูจน์ด้วยคอมพิวเตอร์ แต่การพิสูจน์นี้ไม่เป็นที่ยอมรับจากนักคณิตศาสตร์ส่วนใหญ่ เพราะว่ามันไม่สามารถตรวจสอบด้วยคนได้ และบางคนถึงกับกังวลในความถูกต้องของตัวแปลภาษา (คอมไพเลอร์) และฮาร์ดแวร์ที่ใช้ทำงานโปรแกรมสำหรับการพิสูจน์
การขาดความสง่างามทางคณิตศาสตร์ก็เป็นอีกสาเหตุหนึ่ง ดังคำกล่าวอันหนึ่งว่า "บทพิสูจน์ทางคณิตศาสตร์ที่ดีเป็นดั่งบทกวี — แต่นี่มันคือสมุดจดเบอร์โทรศัพท์ชัดๆ!"
ประวัติ[แก้]
ข้อความคาดการณ์อันนี้ถูกกล่าวถึงครั้งแรกในปี พ.ศ. 2395 (ค.ศ. 1852) เมื่อ ฟรานซิส กูทรี (Francis Guthrie) ได้สังเกตเห็นว่าสามารถใช้เพียงสี่สีก็เพียงพอในการระบาย ขณะที่กำลังระบายแผนที่ของเขตหนึ่งในอังกฤษ ในขณะนั้นกูทรีเป็นลูกศิษย์ของ ออกัสตัส เดอ มอร์แกน (Augustus De Morgan) ที่ ยูนิเวอร์ซิตีคอลเลจลอนดอน (University College London) (กูทรีจบการศึกษาในปี พ.ศ. 2393 (ค.ศ. 1850) และต่อมาได้เป็นศาสตราจารย์สาขาคณิตศาสตร์ในประเทศแอฟริกาใต้) โดยตามคำบอกเล่าของเดอร์มอร์แกน:
- วันนี้ลูกศิษย์ของผมคนหนึ่ง [กูทรี] ขอให้ผมช่วยให้เหตุผลของความจริงอันหนึ่ง - ทั้งที่ผมก็ยังไม่รู้จนถึงบัดนี้เลยว่ามันเป็นความจริง เขาบอกว่า ไม่ว่าเราจะแบ่งรูปออกเป็นส่วนๆในลักษณะใดก็ตาม แล้วระบายสีแต่ละส่วนโดยให้ส่วนที่มีขอบร่วมกันเป็นคนละสีกัน แล้วมันเพียงพอที่จะใช้สีเพียงสี่สี กรณีต่อไปนี้คือกรณีที่ต้องการสี่สีพอดี เรายังไม่สามารถหากรณีที่ต้องการห้าสีหรือมากกว่านั้นได้ ...
หลักฐานอ้างอิงที่มีการตีพิมพ์เป็นอันแรกถูกพบในงานของ อาร์เทอร์ เคย์เลย์ (Arthur Cayley) On the colourings of maps., Proc. Royal Geography Society 1, 259-261, 1879.
นับตั้งแต่ข้อความคาดการณ์นี้ถูกประกาศขึ้นมา ก็มีผู้คนจำนวนมากต้องประสบความล้มเหลวในการพิสูจน์มัน บทพิสูจน์หนึ่งของทฤษฎีบทนี้คืองานของ อัลเฟรด เคมป์ (Alfred Kempe) ในปี พ.ศ. 2422 (ค.ศ. 1879) ซึ่งเป็นชิ้นที่ผู้คนยอมรับกันทั่วไป บทพิสูจน์อีกอันหนึ่งคือของ ปีเตอร์ เทท (Peter Tait) ในปี พ.ศ. 2423(1880) จวบจนกระทั่งปี พ.ศ. 2433 (ค.ศ. 1890) เพอร์ซี เฮวูด (Percy Heawood) จึงได้แสดงว่าบทพิสูจน์ของเคมป์มีข้อผิดพลาด และใน พ.ศ. 2434 (ค.ศ. 1891) จูเลียส ปีเตอร์เซน (Julius Petersen) จึงได้แสดงว่าบทพิสูจน์ของเททผิดพลาด น่าแปลกใจว่าไม่มีผู้ใดเห็นข้อผิดพลาดเหล่านี้ในบทพิสูจน์แต่ละอันถึง 11 ปี
ใน พ.ศ. 2433 (ค.ศ. 1890) นอกจากเฮวูดจะชี้ให้เห็นถึงข้อผิดพลาดของบทพิสูจน์ของเคมป์แล้ว เขายังได้พิสูจน์ว่ากราฟเชิงระนาบทุกอันสามารถระบายได้ด้วยสี 5 สี - ดู ทฤษฎีบทห้าสี
ผลงานที่สำคัญได้ถูกสร้างขึ้นโดยนักคณิตศาสตร์ชาวโครเอเชียชื่อ ดานีโล บลานูซา (Danilo Blanuš) ในช่วงปี พ.ศ. 2483-2492 (1940s) โดยการสร้างสนาร์ค (snark) ต้นแบบขึ้น
ในช่วงปี พ.ศ. 2503-2522 (1960s และ 70s) นักคณิตศาสตร์ชาวเยอรมัน ไฮน์ริค ฮีช (Heinrich Heesch) ได้พัฒนาวิธีการในการใช้คอมพิวเตอร์ช่วยหาบทพิสูจน์
ในพ.ศ. 2512 (ค.ศ. 1969) นักคณิตศาสตร์ชาวอังกฤษ จี สเปนเซอร์-บราวน์ (G. Spencer-Brown) อ้างว่าทฤษฎีบทนี้สามารถพิสูจน์ได้ด้วยระบบคณิตศาสตร์ที่เขาได้พัฒนาขึ้นมา อย่างไรก็ตาม เขาไม่เคยสามารถที่จะสร้างบทพิสูจน์นี้ขึ้นมาจริงๆ ได้
จนกระทั่งปี พ.ศ. 2519 (ค.ศ. 1976) นั่นเอง จึงได้มีผู้พิสูจน์ข้อคาดการณ์สี่สีนี้ได้สำเร็จ โดย เคนเน็ท แอพเพล (Kenneth Appel) และ โวล์ฟแกง เฮเคน (Wolfgang Haken) แห่งมหาวิทยาลัยอิลลินอยส์ เออร์บานา-แชมเปญ โดยได้รับคำปรึกษาทางด้านขั้นตอนวิธีจาก เจ คอช (J. Koch)
บทพิสูจน์เริ่มต้นด้วยการลดรูปแบบของแผนที่ทั้งหมดให้เหลือเพียง 1,936 รูปแบบ (และภายหลังสามารถลดลงเหลือ 1,476 รูปแบบ) จากนั้นจึงนำไปตรวจสอบทีละอันด้วยคอมพิวเตอร์ และมีการตรวจสอบซ้ำสองแยกต่างหากโดยโปรแกรมและเครื่องคอมพิวเตอร์ที่ต่างกัน อย่างไรก็ตามบทพิสูจน์นี้มีความยาวถึง 500 หน้า และเต็มไปด้วยตัวอย่างค้านของตัวอย่างค้าน (counter-counter-example) ที่เขียนด้วยมือ โดยส่วนใหญ่เป็นการทดสอบการระบายสีกราฟ ของลูกชายวัยสิบกว่าๆ ของเฮเคน โปรแกรมคอมพิวเตอร์นี้ใช้เวลาทำงานหลายร้อยชั่วโมง
ในปี พ.ศ. 2539 (ค.ศ. 1996) นีล โรเบิร์ตสัน (Neil Robertson) , แดเนียล แซนเดอร์ส (Daniel Sanders) , พอล ซีมัวร์ (Paul Seymour) และ โรบิน โทมัส (Robin Thomas) สร้างบทพิสูจน์ที่คล้ายๆ กัน แต่มีกรณีที่ต้องทดสอบเพียง 633 กรณี บทพิสูจน์อันใหม่นี้ก็ยังจำเป็นต้องใช้คอมพิวเตอร์ช่วย และเป็นการยากที่จะตรวจสอบด้วยคน
ในปี พ.ศ. 2547 (ค.ศ. 2004) เบนจามิน เวอร์เนอร์ (Benjamin Werner) และ จอร์จส์ กอนทิเออร์ (Georges Gonthier) พิสูจน์ทฤษฎีบทนี้ด้วยใช้โปรแกรมพิสูจน์ทฤษฎีบทชื่อ Coq ซึ่งช่วยลดความจำเป็นที่จะต้องเชื่อในความถูกต้องของโปรแกรมหลายๆ โปรแกรม ที่ใช้ในการสอบกรณีแต่ละกรณี — เหลือเพียงแค่ต้องเชื่อใน Coq เท่านั้น
ตั้งแต่ได้มีการพิสูจน์ทฤษฎีบทนี้สำเร็จ ขั้นตอนวิธีที่มีประสิทธิภาพมากมายก็ได้ถูกสร้างขึ้นสำหรับระบายสีแผนที่ด้วนสี่สี โดยทำงานในเวลาเพียง O(n2) เมื่อ n คือจำนวนจุดยอด นอกจากนี้ยังมีขั้นตอนวิธีทรงประสิทธิภาพที่สามารถตรวจสอบได้ว่าแผนที่ใช้สี 1 หรือ 2 สีระบายได้หรือไม่ สำหรับกรณี 3 สีนั้นเป็นปัญหาเอ็นพีสมบูรณ์ และดังนั้นจึงเป็นไปได้สูงว่าจะไม่มีวิธีการเร็วๆ การตรวจสอบว่ากราฟโดยทั่วไป (ไม่จำเป็นต้องเป็นกราฟเชิงระนาบ) สามารถระบายด้วยสี่สีได้หรือไม่ ก็เป็นปัญหาเอ็นพีสมบูรณ์เช่นกัน
ไม่เกี่ยวกับการทำแผนที่[แก้]
ทฤษฎีบทสี่สีนี้ไม่ได้ถูกค้นพบ หรือมีต้นกำเนิด เกี่ยวข้องใดๆกับการเขียนแผนที่จริงๆ ตามคำกล่าวอ้างของเคนเนธ เมย์ นักประวัติศาสตร์คณิตศาสตร์ ซึ่งได้ศึกษาตัวอย่างของสมุดแผนที่ในห้องสมุดรัฐสภาสหรัฐฯ เขาสรุปว่า ไม่มีข้อบ่งชี้เลยว่าจะมีความพยายามที่จะลดจำนวนสีที่ใช้ แผนที่ส่วนใหญ่ใช้มากกว่าสี่สี และเมื่อใดก็ตามที่ใช้เพียงสี่สี จำนวนสีที่ต้องการจริงๆกลับน้อยกว่านั้น
หนังสือเรียนวิชาการเขียนแผนที่ และประวัติศาสตร์การเขียนแผนที่ ไม่ได้กล่าวถึงทฤษฎีบทสี่สีเลย ถึงแม้ว่าการระบายสีแผนที่จะเป็นหัวข้อหนึ่งที่ให้ความสนใจกัน นักเขียนแผนที่บอกว่า โดยทั่วไปพวกเขาจะสนถึงการระบายสีให้เกิดความสมดุล ไม่ให้มีสีใดกลืนสีอื่นไปหมดมากกว่า เรื่องจำนวนสีไม่ได้อยู่ในความสนใจของพวกเขาเท่าใดนัก
รูปอย่างเป็นทางการในทฤษฎีกราฟ[แก้]
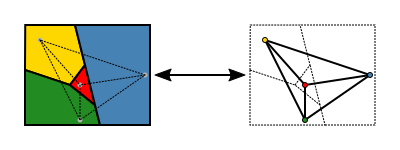
ในการทำทฤษฎีบทสี่สีให้อยู่ในรูปเป็นทางการโดยใช้ทฤษฎีกราฟ เราจะกล่าวว่าจุดยอด (vertices) ในกราฟเชิงระนาบสามารถระบายด้วยสีโดยใช้อย่างมากเพียง 4 สีได้เสมอ โดยไม่มีจุดยอดที่ประชิดกันมีสีเดียวกัน หรือกล่าวสั้นๆ ว่า "กราฟเชิงระนาบทุกกราฟเป็น กราฟ 4 สี (four-colorable) " ทุกพื้นที่ของแผนที่จะถูกแทนด้วยจุดยอดของกราฟ และจุดยอดสองจุดจะเชื่อมกันด้วยเส้นเชื่อม (edge) ก็ต่อเมื่อทั้งสองพื้นที่มีส่วนของขอบร่วมกัน
บทพิสูจน์แย้งที่ผิด[แก้]
ดังเช่นปัญหาคณิตศาสตร์ที่มีชื่อเสียงข้ออื่นๆ ทฤษฎีบทสี่สีได้ก่อให้เกิดบทพิสูจน์และบทพิสูจน์แย้งที่ผิดๆ ขึ้นมากมาย ตลอดประวัติศาสตร์อันยาวนานของมัน บทพิสูจน์บางอัน เช่น งานของเคมป์และเททที่ได้กล่าวถึงไปแล้ว ยืนหยัดต้านทานการตรวจสอบอยู่ในวงการได้นานนับสิบปี ก่อนที่จะมีผู้ค้นพบข้อผิดพลาด แต่งานอื่นๆ อีกหลายชิ้น ซึ่งมักมาจากมือสมัครเล่นและพวกสติไม่เต็ม อาจจะไม่เคยถูกนำมาแสดงต่อสาธารณะเลย
ความพยายามเบื้องต้นที่สุดในการหา "ตัวอย่างค้าน" มักจะเริ่มด้วยการสร้างพื้นที่ที่ติดกับพื้นที่อื่นหลายๆ อัน ซึ่งช่วยบังคับให้บริเวณโดยรอบ ใช้สีจำกัดได้เพียงสามสีเท่านั้น (ถ้าทฤษฎีเป็นจริง) อย่างไรก็ตาม หลายคนอาจสนใจอยู่กับพื้นที่อันใหญ่มากเกินไป จนลืมสังเกตไปว่า ที่จริงแล้วแผนที่สามารถระบายได้ด้วยสีเพียงสามสี
ความผิดพลาดลักษณะนี้ ยังสามารถนำมาพูดในลักษณะที่กว้างขึ้นได้ นั่นคือ หากมีพื้นที่บางส่วนถูกกำหนดสีที่แน่นอนเอาไว้ก่อนแล้ว อาจเป็นไปได้ว่าพื้นที่ส่วนที่เหลือจะไม่สามารถระบายด้วยสี่สีได้ (ทั้งที่ในความจริงแล้ว หากเรายอมให้บางสีที่กำหนดไปแล้วเปลี่ยนแปลงได้ เราก็อาจจะยังสามารถระบายพื้นที่ที่เหลือด้วยสี่สีได้อยู่) ดังนั้นการทดสอบโดยการค่อยๆ ระบายสี จึงมักจะเกิดความผิดพลาดลักษณะนี้ และได้ผลลัพธ์เป็นตัวอย่างค้านแบบผิดๆ
เป็นไปได้ว่าต้นเหตุของความเข้าใจผิดอันนี้ มาจากความจริงที่ว่า การบังคับสีนั้นไม่ได้มีลักษณะถ่ายทอด นั่นคือพื้นที่หนึ่งๆ ถูกบังคับให้มีสีแตกต่างจากพื้นที่ที่ติดกับมันเท่านั้น แต่มันไม่ได้เกี่ยวข้องอะไรกับพื้นที่อันถัดไป (อันที่ติดกับอันที่ติดกับมัน) เลย และถ้าหากคุณสมบัตินี้เป็นจริงขึ้นมา กราฟเชิงระนาบก็คงต้องใช้สีสำหรับระบายจำนวนมหาศาลทีเดียว
บทพิสูจน์แย้งอื่นๆ ก็มักจะทำผิดข้อกำหนดบางอย่างของทฤษฎีบทโดยไม่ได้ตั้งใจ เช่น นำพื้นที่หนึ่งเข้าไปเป็นส่วนหนึ่งของอีกพื้นที่หนึ่ง, สร้างพื้นที่ที่แตกกระจายเป็นหลายส่วนไม่ติดกัน (เช่น มิชิแกน) หรือบังคับไม่ให้พื้นที่ที่มีจุดร่วมกันมีสีเดียวกัน (ที่จริงแล้วข้อกำหนดบังคับเฉพาะพื้นที่ที่มีขอบร่วมกัน)
นัยทั่วไป[แก้]


พิจารณาปัญหาการระบายสีลงบนพื้นผิวใดๆนอกเหนือไปจากระนาบ การระบายสีลงบนพื้นผิวทรงกลมมีลักษณะเดียวกับบนระนาบ สำหรับพื้นผิวแบบปิด(แบบพลิกได้หรือพลิกไม่ได้ก็ได้(orientable or non-orientable)) ที่มีจีนัสเป็นบวก จำนวนสีสูงสุด p ที่ต้องการขึ้นอยู่กับค่าเฉพาะออยเลอร์ χ ของพื้นผิวนั้นๆ ตามสมการ
ข้อยกเว้นเดียวของสมการนี้คือ ขวดไคลน์(Klein bottle) ซึ่งมีค่าเฉพาะออยเลอร์เป็น 0 แต่ต้องการ 6 สี นี่เป็นที่รู้จักกันตอนแรกในฐานะข้อความคาดการณ์เฮวูด และถูกพิสูจน์เป็นทฤษฎีบทการระบายสีแผนที่ โดยเกอร์ฮาร์ด ริงเกล(Gerhard Ringel) และยังส์ (J. T. W. Youngs) ในปีพ.ศ. 2511
ตัวอย่างเช่น ทอรัสมีค่าเฉพาะออยเลอร์ χ = 0 และต้องการ p = 7 สี ในทอรัส แผนที่ทุกๆแบบต้องการสี 7 สีเพื่อระบายมัน
ตัวอย่างค้านจากการใช้งานจริง[แก้]
ในความเป็นจริง บางประเทศอาจไม่ได้มีพื้นที่ติดเป็นแผ่นเดียวกัน (เช่น รัฐอะแลสกา ซึ่งเป็นส่วนหนึ่งของสหรัฐอเมริกา) หากเราบังคับให้พื้นที่ที่เป็นประเทศเดียวกันต้องมีสีเดียวกัน สีจำนวนสี่สีอาจไม่เพียงพอ เนื่องจากเมื่อเขียนแผนที่เป็นกราฟแล้วมันอาจไม่เป็นกราฟเชิงระนาบ ดังนั้นจึงไม่สามารถใช้ทฤษฎีบทสี่สีได้ ตัวอย่างเช่น พิจารณาแผนที่ต่อไปนี้

พื้นที่ A สองอันเป็นของประเทศเดียวกัน ดังนั้นจึงต้องใช้สีเดียวกัน เมื่อเป็นดังนี้ทำให้แผนที่นี้ต้องการห้าสี เนื่องจากพื้นที่ A ทั้งคู่อยู่ติดกับพื้นที่สี่ผืนที่เหลือ และทั้งสี่ผืนต่างก็ติดกับพื้นที่อื่นๆทั้งหมด ถ้า A มีสามผืนแยกจากกัน เราก็จะจำเป็นต้องใช้หกสี และในการสร้างลักษณะนี้ เราสามารถสร้างแผนที่ที่ต้องการสีเท่าใดก็ได้
อ้างอิง[แก้]
- Appel, Kenneth & Haken, Wolfgang & Koch, John, Every Planar map is Four Colorable, Illinois: Journal of Mathematics: vol.21: pp.439-567, December 1977.
- Appel, Kenneth & Haken, Wolfgang, Solution of the Four Color Map Problem, Scientific American, vol.237 no.4: pp.108-121, October 1977.
- Appel, Kenneth & Haken, Wolfgang, Every Planar Map is Four-Colorable. Providence, RI: American Mathematical Society, 1989.
- O'Connor and Robertson, History of the Four Color Theorem, MacTutor project, http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/The_four_colour_theorem.html เก็บถาวร 2013-01-16 ที่ เวย์แบ็กแมชชีน
- Saaty and Kainen, The Four Color Problem: Assaults and Conquest (ISBN 0-486-65092-8)
- Robin Thomas, An Update on the Four-Color Theorem (PDF File) , Notices of the American Mathematical Society, Volume 45, number 7 (August 1998)
- Robin Thomas, The Four Color Theorem, http://www.math.gatech.edu/~thomas/FC/fourcolor.html เก็บถาวร 2007-12-21 ที่ เวย์แบ็กแมชชีน



