การกระจาย (ทัศนศาสตร์)
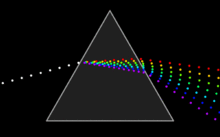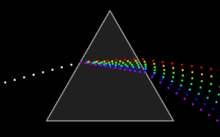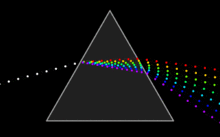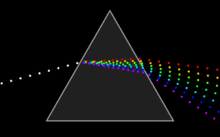
ในทัศนศาสตร์ การกระจาย (dispersion) เป็นปรากฏการณ์ที่ลำแสงที่ตกกระทบถูกแบ่งแยกออกเป็นความยาวคลื่นต่าง ๆ เกิดขึ้นเนื่องจากดรรชนีหักเหในตัวกลางแปรผันไปตามความยาวคลื่น
การกระจายแบบปกติและผิดปกติ[แก้]
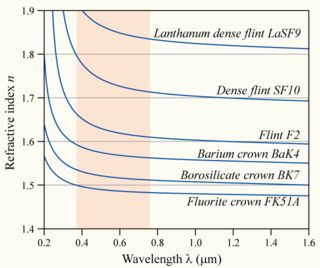
ในกรณีที่ดรรชนีหักเหเพิ่มขึ้นเมื่อความยาวคลื่นลดลง จะเรียกว่าเกิด การกระจายแบบปกติ (normal dispersion) สารที่โปร่งใสในช่วงแสงที่มองเห็นได้จะมีการกระจายแบบปกติในช่วงแสงที่มองเห็นได้ การกระจายแบบปกติยังเกิดขึ้นในบริเวณอื่นที่ไม่ใช่แสงที่มองเห็นได้ในบริเวณที่ห่างจากความยาวคลื่นสั่นพ้องของสสาร นอกจากนี้ โดยทั่วไป ยิ่งวัสดุดรรชนีหักเหสูง การกระจายแบบปกติก็จะยิ่งมากขึ้นเท่านั้น
ในทางกลับกัน ที่ใกล้กับความยาวคลื่นสั่นพ้อง ดรรชนีหักเหจะกลับลดลงและแสงที่มีความยาวคลื่นยาวจะหักเหมากกว่าแสงที่มีความยาวคลื่นสั้น เราเรียกสิ่งนี้ว่า การกระจายแบบผิดปกติ (anomalous dispersion)
สูตรการกระจายตัวของเซ็ลไมเออร์[แก้]
ดรรชนีหักเหของคลื่นนอกเหนือจากย่านใกล้กับความยาวคลื่นสั่นพ้องจะคำนวณได้โดย สมการเซ็ลไมเออร์ (Sellmeier equation)
A′, B′ ,... และ λ A, λ B ,... เป็นตัวแปรช่วยที่แตกต่างกันไปในแต่ละวัสดุ λ A, λ B ,... คือความยาวคลื่นสั่นพ้อง กล่าวคือ มีพจน์มากมาย (นอกเหนือจาก n∞2) เท่ากับความยาวคลื่นสั่นพ้อง
เมื่อดำเนินการกระจายรอบจุดกับ จะได้สูตรต่อไปนี้
สูตรการกระจายของเซ็ลไมเออร์จะให้ผลแตกต่างกันที่ความยาวคลื่นสั่นพ้อง แต่ที่นอกพื้นที่ใกล้เคียงแถบนั้น จะพบว่ามีความตรงกันระหว่างการกระจายแบบปกติกับแบบผิดปกติ สมการที่คำนึงถึงการดูดกลืนนั้นถูกแสดงโดยแฮร์มัน ฟ็อน เฮ็ล์มฮ็อลทซ์
สำหรับตัวกลางที่มีความหนาแน่นสูง จะใช้สูตรการกระจายตัวของเซ็ลไมเออร์ ซึ่งคำนึงถึงความยาวคลื่นของคลื่นสั่นพ้องของไอออนในย่านอินฟราเรด
แก้วเชิงทัศนศาสตร์[แก้]
ความแตกต่างของดรรชนีหักเหที่ความยาวคลื่นอ้างอิงสองช่วง เช่น เส้น F' (สีน้ำเงิน) และ C' (สีแดง) ของเส้นเฟราน์โฮเฟอร์ เรียกว่า ค่าเฉลี่ยการกระจาย หรือ การกระจายหลัก และความแตกต่างของดรรชนีหักเหที่อีกสองค่าความยาวคลื่น นี้เรียกว่า การกระจายบางส่วน การกระจายบางส่วนหารด้วยการกระจายหลักเรียกว่า อัตราส่วนการกระจายบางส่วน
ในแก้วเชิงทัศนศาสตร์ธรรมดานั้นเมื่อวาดกราฟซึ่งมีเลขอับเบอเป็นแกนนอนและอัตราส่วนการกระจายบางส่วนเป็นแกนตั้ง จะได้ค่าที่วางตัวอยู่บนเส้นตรง ซึ่งเรียกว่า การกระจายบางส่วนแบบปกติ ในขณะที่ถ้าเป็นการกระจายแบบผิดปกติจะได้กราฟที่ไม่อยู่บนเส้นตรง ซึ่งเรียกว่า การกระจายบางส่วนแบบผิดปกติ
อ้างอิง[แก้]
- Max Born (2005). 光学の原理 1. แปลโดย 草川徹 ((7th (expanded) ed.) ed.). 東海大学出版会. ISBN 4-486-01678-5.
- 鶴田匡夫 (2004). 第4・光の鉛筆 : 光技術者のための応用光学 (第3版 ed.). 新技術コミュニケーションズ. ISBN 4-915851-15-X.鶴田匡夫 (2004). 第4・光の鉛筆 : 光技術者のための応用光学 (第3版 ed.). 新技術コミュニケーションズ. ISBN 4-915851-15-X.
- 鶴田匡夫 (1990). 応用光学 1. 応用物理工学選書. 培風館. ISBN 4-563-02331-0.



