สมการจรวดซีออลคอฟสกี
ลิงก์ข้ามภาษาในบทความนี้ มีไว้ให้ผู้อ่านและผู้ร่วมแก้ไขบทความศึกษาเพิ่มเติมโดยสะดวก เนื่องจากวิกิพีเดียภาษาไทยยังไม่มีบทความดังกล่าว กระนั้น ควรรีบสร้างเป็นบทความโดยเร็วที่สุด |
สมการจรวดของซีออลคอฟสกี (อังกฤษ: Tsiolkovsky rocket equation) หรือ สมการจรวดอุดมคติ (อังกฤษ: ideal rocket equation) อธิบายถึงการเคลื่อนที่ของยานพาหนะที่เป็นไปตามหลักการพื้นฐานของจรวด: จรวดเป็นอุปกรณ์ที่สามารถประยุกต์ความเร่งของตัวมันเอง (แรงขับดัน) โดยการขับไล่ส่วนหนึ่งของมวลของมันด้วยความเร็วที่สูงออกมาและทำให้เกิดการเคลื่อนที่ไปได้เนื่องมาจากกฏการอนุรักษ์โมเมนตัม สมการนี้มีความเกี่ยวข้องสัมพันธ์กันโดยค่าเดลต้า-วี (การเปลี่ยนแปลงสูงสุดของความเร็วของจรวดถ้าไม่มีแรงภายนอกอื่น ๆ มากระทำ) กับประสิทธิภาพความเร็วไอเสียและมวลเมื่อเริ่มต้นและครั้งสุดท้ายของจรวด (หรือจะเป็นเครื่องยนต์แห่งแรงปฏิกิริยาอื่น ๆ ก็ตามแต่)
สมการคือ:
เมื่อ:
- คือ มวลรวมตอนเริ่มต้น, รวมทั้งมวลของเชื้อเพลิงจรวด,
- คือ มวลรวมตอนสุดท้าย,
- คือ ประสิทธิภาพความเร็วไอเสีย ( เมื่อ คือ แรงดลจำเพาะ มีค่าตามช่วงเวลา, คือ ค่าความเร่งโน้มถ่วงมาตรฐาน),
- คือ เดลต้า-v - การเปลี่ยนแปลงสูงสุดของอัตราเร็วของยานพาหนะ, (เมื่อไม่มีแรงภายนอกมากระทำ),: หมายถึงฟังก์ชันลอการิทึมธรรมชาติ,
หน่วยที่ใช้สำหรับมวลหรือความเร็วนั้นไม่สำคัญตราบเท่าที่พวกมันยังมีความสอดคล้องกัน
สมการถูกตั้งตามชื่อของคอนสแตนติน ซีออลคอฟสกี ซึ่งเป็นผู้ที่คิดขึ้นมาและผลงานของเขาได้รับการตีพิมพ์ในปี 1903 [1]
ประวัติ[แก้]
สมการนี้มีที่มาอย่างอิสระโดย คอนสแตนติน ซีออลคอฟสกี (Konstantin Tsiolkovsky) ในช่วงปลายของศตวรรษที่ 19 และเป็นที่รู้จักกันอย่างกว้างขวางในนามภายใต้ชื่อของเขาหรือเป็น 'สมการจรวดในอุดมคติ' อย่างไรก็ดีหนังสือเล่มเล็ก ๆ ที่เพิ่งค้นพบเมื่อไม่นานมานี้คือ "ตำราเกี่ยวกับการเคลื่อนที่ของจรวด" (A Treatise on the Motion of Rockets) โดยวิลเลียม มัวร์ (William Moore) [2] ได้แสดงให้เห็นว่าแหล่งที่มาของสมการนี้ที่รู้จักกันเป็นครั้งแรกในข้อเท็จจริงคือมาจากโรงเรียนนายร้อยทหารบกแห่งวัลลิช (Royal Military Academy at Woolwich) ในประเทศอังกฤษในปี 1813,[3] และได้ถูกนำมาใช้สำหรับการวิจัยอาวุธ
ที่มา[แก้]
ในแหล่งที่มาดังต่อไปนี้ คำว่า "จรวด" จะถูกนำไปใช้ในความหมายว่า "จรวดและเชื้อเพลิงจรวดที่ยังไม่ถูกเผาไหม้ทั้งหมด"
กฎข้อที่สองของนิวตันของการเคลื่อนที่เกี่ยวข้องกับแรงภายนอก () ไปสู่การเปลี่ยนแปลงในโมเมนตัมเชิงเส้นของระบบดังต่อไปนี้:
เมื่อ คือ โมเมนตัมของจรวดที่เวลา t=0:
และ คือ โมเมนตัมของจรวดและโมเมนตัมของมวลไอเสียที่เวลา :
และเมื่อเทียบกับผู้สังเกต:
คือ ความเร็วของจรวดที่เวลา t=0 คือ ความเร็วของจรวดที่เวลา คือ ความเร็วของมวลที่เพิ่มขึ้นให้กับไอเสีย (และมวลที่สูญเสียไปของจรวด) ในระหว่างช่วงเวลา คือ มวลของจรวดที่เวลา t=0 คือ มวลของจรวดที่เวลา
ความเร็วของไอเสีย อยู่ในกรอบของผู้สังเกตการณ์ที่สัมพันธ์กับความเร็วของไอเสีย ในกรอบของจรวดโดย (เนื่องจากความเร็วของไอเสียเป็นไปในทิศทางที่เป็นลบ)
ดังนั้น จะได้
และ, โดยใช้ , เนื่องจากขณะดันออก เป็นบวก จึงส่งผลให้เกิดการลดลงของมวล,
ถ้าไม่มีแรงภายนอกแล้ว และ
สมมติว่า เป็นค่าคงที่, นี่อาจจะทำการอินทิเกรทให้ได้ผลเป็น:
หรือสมมูลกับ
- หรือ หรือ
เมื่อ คือ มวลรวมเริ่มต้นรวมทั้งเชื้อเพลิงจรวด, คือ มวลรวมสุดท้าย และ คือ ความเร็วของไอเสียจรวดส่วนที่เกี่ยวกับจรวด (แรงดลจำเพาะ, หรือหากวัดในเวลาจะคูณด้วยอัตราเร่งเนื่องจากแรงโน้มถ่วงของโลก)
ค่า เป็นมวลรวมของเชื้อเพลิงจรวดที่ถูกใช้, และด้วยเหตุนี้:
เมื่อ เป็นเศษส่วนมวลของเชื้อเพลิงจรวด (ส่วนหนึ่งของมวลรวมเริ่มต้นที่ใช้เป็นมวลปฏิกิริยา)
(เดลต้า v) คือการอินทิเกรทในช่วงเวลาของขนาดของความเร่งที่ผลิตโดยใช้เครื่องยนต์จรวด (สิ่งที่จะเป็นความเร่งที่เกิดขึ้นจริงถ้าแรงจากภายนอกไม่มี) ในพื้นที่ว่าง (หรือ อวกาศอิสระ), สำหรับกรณีของความเร่งในทิศทางของความเร็ว, นี้คือการเพิ่มขึ้นของความเร็ว ในกรณีที่มีความเร่งในทิศทางตรงข้าม (ชะลอความเร็วลง) มันคือการลดลงของอัตราเร็ว แน่นอนว่าแรงโน้มถ่วงและแรงฉุดก็คือตัวทำให้เกิดความเร่งต่อจรวด, และสามารถเพิ่มหรือลดลงได้ในการเพื่อที่จะเปลี่ยนแปลงความเร็วของมันโดยการได้รับประสบการณ์จากการควบคุมอากาศยานลำนั้น ๆ นั่นเอง ดังนั้น เดลต้า-v มักจะไม่ได้มีการเปลี่ยนแปลงที่เกิดขึ้นจริงในอัตราเร็วหรือความเร็วของอากาศยาน
ถ้าทฤษฎีสัมพัทธภาพพิเศษถูกนำมาพิจารณา, สมการดังต่อไปนี้จะสามารถได้มาจากการเคลื่อนที่แบบจรวดเชิงสัมพัทธ (relativistic rocket), [4] ด้วย อีกครั้งโดยถูกกำหนดให้เป็นความเร็วสุดท้ายของจรวด (หลังจากการเผาไหม้เชื้อเพลิงออกไปหมดและมีการลดลงของมวลส่วนที่เหลือ ) ในกรอบอ้างอิงเฉื่อยเมื่อจรวดเริ่มต้นเคลื่อนที่ที่จุดหยุดนิ่ง (ที่มีมวลส่วนที่เหลือรวมทั้งเชื้อเพลิงที่เป็น ในตอนเริ่มต้น) และ ถูกกำหนดให้เป็นค่าสำหรับอัตราเร็วของแสงในสูญญากาศ:
การเขียน ให้เป็น , ด้วยพีชคณิตเล็ก ๆ น้อย ๆ แบบนี้จะช่วยทำให้สมการนี้ได้รับการปรับปรุงใหม่เป็น
จากนั้นใช้เอกลักษณ์ (ในที่นี่ "exp" หมายถึงฟังก์ชันเอกซ์โพเนนเชียล (exponential function); ดูเพิ่มเติม ลอการิทึมธรรมชาติ มีค่าเช่นเดียวกับ "ยกกำลัง" ของเอกลักษณ์ของเอกลักษณ์ลอการิทึม (Logarithmic identities) และเอกลักษณ์ (ดู ฟังก์ชันไฮเพอร์โบลิก (Hyperbolic function)) นี้จะเทียบเท่ากับ
ดูเพิ่ม[แก้]
- Delta-v
- Delta-v budget
- Oberth effect
- Specific impulse
- Spacecraft propulsion
- Mass ratio
- Working mass
- Relativistic rocket
- Reversibility of orbits
- Variable-mass systems
อ้างอิง[แก้]
- ↑ К. Э. Циолковский, Исследование мировых пространств реактивными приборами, 1903. It is available online here เก็บถาวร 2011-08-15 ที่ เวย์แบ็กแมชชีน in a RARed PDF
- ↑ Moore, William; of the Military Academy at Woolwich (1813). A Treatise on the Motion of Rockets. To which is added, An Essay on Naval Gunnery. London: G. and S. Robinson.
- ↑ Johnson, W. (1995). "Contents and commentary on William Moore's a treatise on the motion of rockets and an essay on naval gunnery". International Journal of Impact Engineering. 16 (3): 499–521. doi:10.1016/0734-743X(94)00052-X. ISSN 0734-743X.
- ↑ Forward, Robert L. "A Transparent Derivation of the Relativistic Rocket Equation" เก็บถาวร 2018-09-06 ที่ เวย์แบ็กแมชชีน (see the right side of equation 15 on the last page, with R as the ratio of initial to final mass and w as the exhaust velocity, corresponding to ve in the notation of this article)










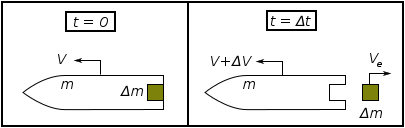
































![{\displaystyle {\frac {m_{0}}{m_{1}}}=\left[{\frac {1+{\frac {\Delta v}{c}}}{1-{\frac {\Delta v}{c}}}}\right]^{\frac {c}{2v_{e}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80b17588a3cf48740fdf5e53bb7d9a6d38ebf9d)



![{\displaystyle R^{\frac {2v_{e}}{c}}=\exp \left[{\frac {2v_{e}}{c}}\ln R\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7466886986a08129e115343fbab4b9d624056dc)

