การลบ
บทความนี้ไม่มีการอ้างอิงจากแหล่งที่มาใด |

การลบ (อังกฤษ: subtraction) ในคณิตศาสตร์เป็นหนึ่งในสี่การดำเนินการพื้นฐานของเลขคณิต มักเขียนแทนด้วยการเติมเครื่องหมายลบ
ชื่อของแต่ละพจน์ของการลบ
- c − b = a
คือ ผลลบ (a), ตัวตั้งลบ (c), ตัวลบ (b)
เครื่องหมาย
[แก้]การลบมักจะเขียนโดยใช้เครื่องหมายลบ "−" ระหว่างเทอม คำตอบจะอยู่หลังเครื่องหมายเท่ากับ เช่น
- (อ่านว่า "สองลบหนึ่งเท่ากับหนึ่ง")
- (อ่านว่า "สี่ลบสองเท่าหับสอง")
- (อ่านว่า "หกลบสามเท่ากับสาม")
- (อ่านว่า "สี่ลบหกเท่ากับลบสอง")
การลบพื้นฐาน
[แก้]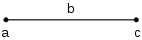
เส้นตรงที่มีความยาว b ซึ่งปลายด้านซ้ายเขียนว่า a และปลายด้านขวาเขียนว่า c
เริ่มต้นที่ตำแหน่ง a ถ้าเดินไปทางขวา b ก้าว จะไปอยู่ตำแหน่งที่ c การเคลื่อนที่ไปทางขวานี้เรียกว่า การบวก สามารถเขียนได้ว่า
- a + b = c
จากตำแหน่ง c ถ้าเดินไปทางซ้าย b ก้าว จะไปอยู่ตำแหน่งที่ a การเคลื่อนที่ไปทางซ้ายนี้เรียกว่า การลบ สามารถเขียนได้ว่า
- c − b = a

เส้นตรงที่เขียนเลข 1, 2 และ 3
จากตำแหน่ง 3 ถ้าไม่เดินเลยสักก้าว จะอยู่ตำแหน่งที่ 3 เหมือนเดิม ดังนั้น
- 3 − 0 = 3
จากตำแหน่ง 3 ถ้าเดินไปทางซ้าย 1 จะไปอยู่ตำแหน่งที่ 2 ดังนั้น
- 3 − 1 = 2
จากตำแหน่ง 3 ถ้าเดินไปทางซ้าย 2 จะไปอยู่ตำแหน่งที่ 1 ดังนั้น
- 3 − 2 = 1
ถ้าเดินไปทางซ้าย 3 ก้าวจากตำแหน่งที่ 3 จะเดินออกนอกเส้นซึ่งทำไม่ได้ ดังนั้น ถ้าการดำเนินการนี้จะใช้ได้ เส้นจะต้องขยายออกไปกว่านี้
สำหรับการลบของจำนวนธรรมชาติ เส้นจะมีจำนวนธรรมชาติทุก ๆ จำนวน (0, 1, 2, 3, 4, ...) อยู่บนเส้น
ใช้เส้นจำนวนธรรมชาติ จากตำแหน่งที่ 3 ถ้าเดินไปทางซ้าย 3 ก้าว จะไปถึงตำแหน่งที่ 0 ดังนั้น
- 3 − 3 = 0
แต่สำหรับจำนวนธรรมชาติ 3 − 4 จะใช้ไม่ได้ตั้งแต่ที่มันเริ่มเดินออกจากเส้น ดังนั้น ถ้าการดำเนินการนี้จะใช้ได้ เส้นจะต้องขยายออกไปกว่านี้
ใช้เส้นจำนวนเต็ม (…, −3, −2, −1, 0, 1, 2, 3, …) จากตำแหน่งที่ 3 ถ้าเดินไปทางซ้าย 4 ก้าว จะไปอยู่ที่ตำแหน่งที่ −1 ดังนั้น
- 3 − 4 = −1




