ปัญหามอนตี ฮอลล์
บทความนี้ได้รับแจ้งให้ปรับปรุงหลายข้อ กรุณาช่วยปรับปรุงบทความ หรืออภิปรายปัญหาที่หน้าอภิปราย
|

ปัญหามอนตี ฮอลล์ หรือ เกมประตูดวง (อังกฤษ: Monty Hall problem) เป็นปริศนาทางคณิตศาสตร์เกี่ยวกับความน่าจะเป็น เนื้อหาของปริศนาระบุว่า
- สมมติว่าผู้เล่นเกมโชว์มีประตูสามบานให้เลือก หลังประตูบานหนึ่งจะมีรางวัลอยู่ (มักจะบรรยายว่าเป็นรถยนต์) ส่วนหลังประตูบานที่เหลือไม่มีรางวัล (มักจะบรรยายว่ามีแพะอยู่หลังประตู) ผู้เล่นเลือกประตูหนึ่งบาน (สมมติว่าเรียกว่าประตูบานที่ 1) เมื่อผู้เล่นเลือกแล้ว พิธีกรซึ่งรู้ว่าหลังประตูแต่ละบานมีรางวัลหรือไม่ จะเปิดประตูอีกบานหนึ่งซึ่งไม่มีรางวัล (สมมติว่าเป็นประตูบานที่ 3) หลังจากนั้น พิธีกรจะให้โอกาสผู้เล่นในการเปลี่ยนไปเลือกประตูอีกบานหนึ่งที่ไม่ได้เลือกในตอนแรก (บานที่ 2) คำถามคือ การเปลี่ยนไปเลือกประตูที่ไม่ได้เลือกตอนแรก จะทำให้มีความน่าจะเป็นในการได้รางวัลมากขึ้นหรือไม่
ปัญหามอนตี ฮอลล์ได้รับการกล่าวถึงครั้งแรกในจดหมายของสตีฟ เซลวิน ที่ตีพิมพ์ในวารสาร American Statistician ในปี 1975 และมาได้รับความสนใจจากสาธารณชนเมื่อมาริลิน วอส ซาวานท์ เขียนถึงปัญหานี้ในนิตยสาร Parade ในปี 1990 ชื่อปัญหามอนตี ฮอลล์ มีที่มาจากรายการเกมโชว์ในสหรัฐอเมริกาชื่อว่า Let's Make a Deal ซึ่งมีมอนตี ฮอลล์ เป็นพิธีกร โดยมีเกมโชว์ภาษาไทยที่มีลักษณะเดียวกันชื่อประตูดวง ปัญหานี้มีชื่อเรียกอีกชื่อหนึ่งว่า มอนตี ฮอลล์ พาราดอกซ์ (Monty Hall paradox) เนื่องจากคำตอบของปัญหานั้นค่อนข้างจะสวนกับสามัญสำนึก ถึงแม้ว่าปัญหานี้จะไม่ได้เป็นพาราดอกซ์จริง ๆ ก็ตาม
คำตอบของปริศนานี้คือ หากว่าผู้เล่นเปลี่ยนประตูบานที่เลือก จะมีความน่าจะเป็นที่ได้รับรางวัลเท่ากับ 23 และถ้ายืนยันเลือกประตูบานเดิม จะมีความน่าจะเป็นที่จะได้รับรางวัลเท่ากับ 13 แต่คำตอบนี้มีลักษณะสวนทางกับสามัญสำนึก ทำให้เมื่อวอส ซาวานท์ อธิบายคำตอบข้างต้น ผู้อ่านประมาณหนึ่งหมื่นคนเขียนจดหมายมาถึงนิตยสารว่าคำตอบนี้ไม่ถูกต้อง
ปัญหา และ คำตอบ[แก้]
เงื่อนไข ของปัญหา[แก้]
รายละเอียดของปํญหา
- หลังประตู 3 บาน จะมี แพะ หรือ รถ อยู่ โดยมี 1 ประตูที่มีรถยนต์ และ 2 ประตูที่มีแพะ
- ผู้เล่นเลือก 1 ประตูจาก 3 ประตู แต่ยังไม่เปิดดูว่ามีอะไรอยู่หลังประตู
- ผู้ดำเนินรายการรู้ล่วงหน้าว่ามีอะไรอยู่หลังประตูแต่ละบาน
- ผู้ดำเนินรายการจะต้องเปิดประตู 1 บานจากประตูที่เหลืออยู่ และ ให้โอกาสผู้เล่นเลือกเปลี่ยน
- ผู้ดำเนินรายการจะเปิดประตูที่มีแพะอยู่เสมอ
- ถ้าประตูที่ผู้เล่นเลือกไว้มีแพะอยู่ ผู้ดำเนินรายการจะเลือกเปิดประตูที่มีแพะอีกประตูที่เหลืออยู่
- ถ้าประตูที่ผู้เล่นเลือกไว้มีรถยนต์อยู่ ผู้ดำเนินรายการจะสุ่มเลือกเปิดประตูใดประตูหนึ่งจาก 2 ประตูที่เหลืออยู่
- ผู้ดำเนินรายการ ให้โอกาสแก่ผู้เล่นในการเลือกว่าจะ เลือกประตูเดิมที่เลือกไว้แล้ว หรือจะสลับกับประตูที่เหลืออยู่
คำถาม คือ โอกาสที่ผู้เล่นจะเลือกรถยนต์จะเพิ่มขึ้นหรือไม่ จะผู้เล่นเลือกที่จะสลับประตู บานที่เลือกไว้กับบานที่เหลืออยู่?
คำตอบ[แก้]
คำตอบของปัญหานี้คือ ผู้เล่นควรจะ สลับประตู โอกาสที่ผู้เล่นจะเลือกได้รถนั้นจะเพิ่มขึ้นเป็นสองเท่า หากผู้เล่นเลือกสลับประตูที่เลือกไว้เดิมกับประตูที่เหลืออยู่
กำหนดให้สิ่งที่อยู่หลังประตู คือ รถยนต์ แพะหมายเลข 1 และ แพะหมายเลข 2 รูปแบบของเหตุการณ์ที่เกิดขึ้นได้มี 3 แบบ แต่ละแบบมีความน่าจะเป็น 1/3 เท่า ๆ กัน คือ
- ผู้เล่นเลือกถูก แพะหมายเลข 1 ผู้ดำเนินรายการเลือก แพะที่เหลืออยู่คือ หมายเลข 2 และ ผู้เล่น สลับประตูจะได้รถยนต์
- ผู้เล่นเลือกถูก แพะหมายเลข 2 ผู้ดำเนินรายการเลือก แพะที่เหลืออยู่คือ หมายเลข 1 และ ผู้เล่น สลับประตูจะได้รถยนต์
- ผู้เล่นเลือกถูก รถ ผู้ดำเนินรายการเลือกประตูหนึ่งจากประตูที่เหลือ และ และ ผู้เล่น สลับประตูจะไม่ได้รถยนต์
จะเห็นว่า สองกรณีแรกนั้น ผู้เล่นได้รถยนต์ด้วยการสลับ และ กรณีที่สามเพียงกรณีเดียวเท่านั้นที่ ได้รถยนต์ด้วยการไม่สลับ ดังนั้นโอกาสในการถูกรางวัลด้วยการสลับประตูนั้นจะเป็น 2/3 และ ไม่สลับประตูจะเป็น 1/3
หรือ อาจอธิบายได้อีกทางหนึ่งก็คือ สมมุติไว้ก่อนว่าคุณจะสลับประตู ดังนั้นวิธีที่คุณจะได้รถยนต์ก็คือ ต้องเลือกประตูที่ไม่มีรถยนต์อยู่ ซึ่งใน 2 ประตูที่ไม่เลือกจะมี 1 ประตูที่มีแพะ และ 1 ประตูที่มีรถยนต์ ประตูที่มีแพะนั้นจะถูกเลือกเปิดโดยผู้ดำเนินรายการ และ เมื่อสลับประตูคุณจะได้รถยนต์ จะเห็นได้ว่าโอกาสที่คุณจะต้องเลือกให้ได้ประตูที่ไม่มีรถยนต์อยู่ในตอนแรกสุดนั้นเป็น 2/3 ซึ่งก็คือโอกาสในการถูกรางวัลรถยนต์ หากสลับประตู
คำอธิบายเพิ่มเติม[แก้]
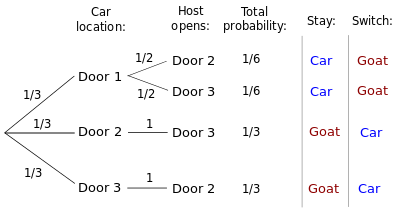
แผนผังแสดงความน่าจะเป็น[แก้]
ตัวอย่าง[แก้]
สมมุติว่า:
ประตู 1 - รถยนต์ ประตู 2 - แพะ ประตู 3 - แพะ
กรณีที่ 1: คุณเลือกประตู 1. ผู้ดำเนินรายการเปิดประตู 3 ให้ดูว่าเป็นแพะ ก) คุณอยู่กับประตู 1 = คุณชนะ ข) คุณสลับไปประตู 2 = คุณแพ้
กรณีที่ 2: คุณเลือกประตู 2. ผู้ดำเนินรายการเปิดประตู 3 ให้ดูว่าเป็นแพะ ก) คุณอยู่กับประตู 2 = คุณแพ้ ข) คุณสลับไปประตู 1 = คุณชนะ
กรณีที่ 3: คุณเลือกประตู 3. ผู้ดำเนินรายการเปิดประตู 2 ให้ดูว่าเป็นแพะ ก) คุณอยู่กับประตู 3 = คุณแพ้ ข) คุณสลับไปประตู 1 = คุณชนะ
จะเห็นได้ว่าถ้าคุณสลับประตู คุณจะมีโอกาสชนะ 2/3 ครั้ง หรือ 66.66% แต่ถ้าคุณอยู่กับประตูเดิม คุณจะมีโอกาสชนะ 1/3 ครั้ง หรือ 33.33%
ทฤษฎีของเบย์[แก้]
ให้
- : ผู้ดำเนินรายการเปิดประตู หมายเลข i
- : รถยนต์อยู่หลังประตูหมายเลข i
การวิเคราะห์ความน่าจะเป็นตามทฤษฎีของเบย์ สมมุติในตอนแรกผู้เล่นเลือกประตูหมายเลข 3 ความน่าจะเป็นที่รถยนต์อยู่หลังประตูหมายเลข 2 คือ มีค่าเท่ากับ 1/3 จากนั้นความน่าจะเป็นที่ผู้ดำเนินรายการจะเปิดประตูหมายเลข 1 มีค่าเท่ากับ 1/2 คือเลือกจากประตูหมายเลข 1 หรือ 2 แต่จากข้อมูลที่ผู้ดำเนินรายการมีอยู่ ผู้ดำเนินรายการจะไม่เปิดประตูที่มีรถยนต์อยู่ด้านหลัง ดังนั้น ในกรณีที่รถยนต์อยู่หลังประตูหมายเลข 2 ผู้ดำเนินจะถูกบังคับให้เปิดประตูหมายเลข 1 ซึ่งก็คือ และ และ ความน่าจะเป็นที่รถยนต์จะอยู่หลังประตูหมายเลข 2 ถ้าหากผู้ดำเนินรายการเลือกเปิดประตูหมายเลข 1 คือ