NOR (ตรรกศาสตร์)
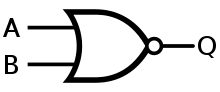
ในตรรกะแบบบูล ตรรกะ nor หรือ การปฏิเสธแบบร่วม (อังกฤษ: joint denial) เป็นการดำเนินการทางตรรกะที่ผลผกผันกับตรรกะ or โดยที่ p nor q เป็นจริงได้ก็ต่อเมื่อทั้ง p และ q เป็น เท็จ
NOR รู้จักกันในอีกชื่อหนึ่งคือ Webb-operation หรือ Peirce arrow ซึ่งได้ชื่อตาม Charles Peirce ผู้พิสูจน์ว่าการดำเนินการทางตรรกะสามารถแสดงในรูปพจน์ของ NOR เหมือนกับ ตรรกะ NAND เราสามารถใช้ NOR เพียงตรรกะเดียว โดยไม่ใช้ตรรกะอื่นมาประกอบเป็นระบบตรรกะได้ (ใช้วิธี NOR functionally complete) หรือที่รู้จักกันในชื่อ Quine's dagger
นิยาม[แก้]
NORเป็นการดำเนินการตรรกะบนค่าตรรกะสองค่า ถ้ามีตัวดำเนินการทางตรรกศาสตร์ 2 ค่า จะใด้ค่า จริง ก็ต่อเมื่อตัวถูกดำเนินการทั้งสองเป็นเท็จ ในกรณีอื่นๆจะให้ค่าเป็น เท็จ ถ้ามีตัวถูกดำเนินการค่าใดค่าหนึ่งเป็นจริงเพียงค่าเดียวหรือเป็นจริงทั้งคู่
ตารางค่าความจริง[แก้]
ตารางค่าความจริง ของ p NOR q (หรือเขียนตาม p ⊥ q หรือ p ↓ q) เป็นดังนี้:
| p | q | ↓ |
|---|---|---|
| T | T | F |
| T | F | F |
| F | T | F |
| F | F | T |
แผนภาพเวนน์[แก้]
แผนภาพเวนน์ของ "A nor B" (ในพื้นที่สีแดงค่าเป็นจริง)
เราสามารถเขียนแทน p NOR q ด้วย , โดยที่สัญลักษณ์ แทน OR และขีดบนแทนสัญลักษณ์นิเสธที่ตรรกะที่แสดงอยู่ภายใต้ ซึ่งเขียนโดยทั่วไปในรูป หรือเขียนแทน p NOR q ด้วย
การปฏิเสธแบบร่วม[แก้]
NOR มีลักษณะที่น่าสนใจโดยตัวดำเนินการตรรกะอื่นๆสามารถแสดงในรูปแบบฟังก์ชันของ NOR
| "not p" is equivalent to "p NOR p" | |
| "p and q" สมมูลในรูป "(p NOR p) NOR (q NOR q)" | |
| "p or q" สมมูลในรูป "(p NOR q) NOR (p NOR q)" | |
| "p implies q" สมมูลในรูป "((p NOR q) NOR q) NOR ((p NOR q) NOR q)" |
ตรรกะ NAND มีความสามารถแสดงแทนได้เช่นกัน
ดูเพิ่ม[แก้]
|
|
- PlanetMath entry on "Ampheck" เก็บถาวร 2008-09-27 ที่ เวย์แบ็กแมชชีน









