ขั้นตอนวิธีของครูสกาล
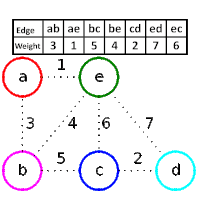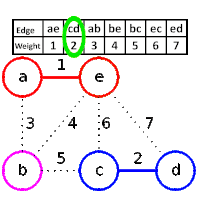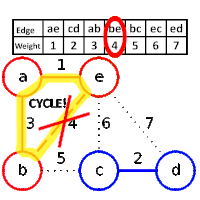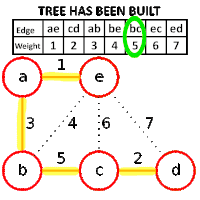
ขั้นตอนวิธีของครูสกาล (อังกฤษ: Kruskal's algorithm) เป็นขั้นตอนวิธีแบบละโมบในทฤษฎีกราฟ ที่ใช้หา ต้นไม้แบบทอดข้ามน้อยสุด (Minimum spanning tree) สำหรับกราฟเชื่อมโยงแบบมีน้ำหนัก นั้นหมายความว่าเราจะได้เซตย่อยของเส้นเชื่อมในต้นไม้ที่เชื่อมทุกๆปม โดยที่ผลรวมของน้ำหนักบนเส้นเชื่อมจะมีค่าน้อยที่สุด หากกราฟไม่เป็นกราฟเชื่อมโยง เราจะได้ ป่าแบบทอดข้ามน้อยสุด (คือต้นไม้แบบทอดข้ามน้อยสุดแต่ละต้นในกราฟ)
ขั้นตอนวิธีนี้ปรากฏครั้งแรกบนนิตยสารทางวิทยาศาสตร์ชื่อ Proceedings of the American Mathematical Society หน้า. 48-50 ในปี 1956, และเขียนโดย โจเซฟ ครูสกาล
และยังมีขั้นตอนวิธีสำหรับแก้ปัญหาแบบเดียวกัน เช่น ขั้นตอนวิธีของพริม ขั้นตอนวิธีการลบย้อนกลับ และ ขั้นตอนวิธีของโบรุฟกา
อธิบาย[แก้]
- สร้างป่า F (เซตของต้นไม้) ที่มีจุดยอดหรือปมในกราฟเป็นต้นไม้
- สร้างเซต S ที่บรรจุทุกเส้นเชื่อมในกราฟไว้
- ในขณะที่ S ไม่เป็นเซตว่าง และ F ยังไม่ทอดข้าม
- ลบเส้นเชื่อมที่มีน้ำหนักน้อยที่สุดจาก S
- ถ้าเส้นเชื่อมนั้นเชื่อมจุดสองจุดที่ต่างกันบนต้นไม้ แล้วเพิ่มเข้าไปในป่าดังกล่าวรวมต้นไม้สองต้นให้เป็นต้นเดียว
เมื่อขั้นตอนวิธีสิ้นสุดลง ป่าจะอยู่ในรูปป่าแบบทอดข้ามน้อยสุดของกราฟ ถ้ากราฟเป็นกราฟเชื่อมโยง ป่าดังกล่าวจะประกอบกันในรูปของต้นไม้แบบทอดข้ามน้อยสุด
รหัสเทียม[แก้]
จากรหัสสามารถทำให้เกิดผลด้วยโครงสร้างข้อมูลแบบเซตไม่ต่อเนื่อง (disjoint-set data structure)
KRUSKAL(G):
1 A = ∅
2 foreach v ∈ G.V:
3 MAKE-SET(v)
4 foreach (u, v) ordered by weight(u, v), increasing:
5 if FIND-SET(u) ≠ FIND-SET(v):
6 A = A ∪ {(u, v)}
7 UNION(u, v)
8 return A
ประสิทธิภาพ[แก้]
ถ้า E คือจำนวนเส้นเชื่อมในกราฟ และ V คือจำนวนของจุดยอด ขั้นตอนวิธีนี้สามารถทำงานได้ในเวลา O(E log E) หรือเท่ากับ O(E log V) โดยในทุกโครงสร้าข้อมูล เวลาการทำงานจะเท่าเทียมกันเพราะ:
- E มีค่ามากที่สุดประมาณ และ นั่นคือ O(log V)
- แต่ละจุดยอดเดี่ยวเป็นส่วนประกอบแยกของป่าแบบทอดข้ามน้อยสุด ถ้าเราไม่สนใจจุดยอดเดี่ยว เราจะได้ V ≤ E+1 ดังนั้น log V คือ O(log E)
เราสามารถเพิ่มประสิทธิภาพได้ดังนี้ เริ่มจากเรียงลำดับเส้นเชื่อมตามน้ำหนักใช้เวลา O(E log E) ขั้นตอนนี้อนุญาตให้ ลบเส้นเชื่อมที่มีน้ำหนักน้อยที่สุดจาก S เพื่อที่จะดำเนินการในเวลาคงที่ ขั้นตอนต่อไปเราใช้ ข้อมูลแบบเซตไม่ต่อเนื่อง เพื่อเก็บลู่ของจุดยอดต้องการการปฏิบัติการใน O(E) การดำเนินการ ทุกๆ โครงสร้างข้อมูลแบบเซตไม่ต่อเนื่อง สามารถทำได้ปฏิบัติการได้ใน O(E) การดำเนินการ ในเวลา O(E log V) ดังนั้นจะได้เวลารวม O(E log E) = O(E log V)
ถ้าได้เรียงลำดับเส้นเชื่อมก่อนแล้วหรือสามารถเรียงดำลับในเวลาเชิงเส้น (เช่น การเรียงลำดับแบบนับจำนวน (counting sort)) หรือ การเรียงลำดับแบบสมุฎฐาน (radix sort)) ขั้นตอนวิธีนี้ลดความซับซ้อนของโครงสร้างข้อมูลแบบเซตไม่ต่อเนื่อง เพื่อลดเวลาการทำงานใน O(E α(V)) เมื่อ α เป็นค่าที่มีอัตราการเติบโตน้อยมากๆ
ตัวอย่าง[แก้]
ดาวน์โหลดข้อมูลตัวอย่าง เก็บถาวร 2012-07-16 ที่ เวย์แบ็กแมชชีน
| รูปภาพ | คำอธิบาย |
|---|---|

|
AD และ CE เป็นเส้นเชื่อมที่สั้นที่สุดมีความยาว 5 หน่วย แล้วทำการเลือก AD โดยพลการ และทำการเน้นเส้นเชื่อมนั้น |

|
CE เป็นเส้นเชื่อมที่สั้นที่สุด ณ ตอนนี้ที่ไม่เป็นวัฏจักรโดยมีความยาว 5 แล้วทำการเน้นเป็นเส้นเชื่อมที่สอง |

|
เส้นเชื่อมต่อไปคือ DF มีความยาว 6 หน่วย ได้ถูกเน้นตามวิธีการเดิม |

|
เส้นเชื่อมที่สั้นที่สุดต่อไปคือ AB และ BE ทั้งคือมีความยาว 7 หน่วย เลือก AB โดยใช้หลักพลการ เส้นเชื่อม BD ได้ถูกเน้นเป็นสีแดงเพราะมันอยู่ในแนวเดินระหว่าง B และ D อยู่แล้ว ดังนั้นถ้าเราเลือกจะเกิดวัฏจักรขึ้น (ABD) |

|
กระทำเช่นเดิมไปเรื่อยๆทำการเน้นเส้นเชื่อมที่สั้นที่สุดต่อไป BE ยาว 7 หน่วย และหลายๆเส้นเชื่อมจะถูกเน้นสีแดง: BC เพราะจะเกิดวงวน BCE DE เพราะจะเกิดวงวน DEBA และ FE เพราะจะเกิด FEBAD |

|
ในที่สุด เมื่อกระบวนการเสร็จสิ้นโดยเลือก EG ยาว 9 หน่วยก็จะได้ต้นไม้แบบทอดข้ามน้อยที่สุด |
พิสูจน์ความถูกต้อง[แก้]
การพิสูจน์ประกอบไปด้วยสองส่วน คือ ส่วนแรกเป็นการพิสูจน์ว่าขั้นตอนวิธีนี้สร้างต้นไม้แบบทอดข้ามได้ ส่วนที่สองคือพิสูจน์ว่าต้นไม้ทอดข้ามดังกล่าวมีน้ำหนักรวมน้อยที่สุด
ต้นไม้ทอดข้าม[แก้]
ให้ P เป็นกราฟเชื่อมโยงที่มีน้ำหนัก และให้ Y เป็นกราฟย่อยของ P ที่สร้างโดยขั้นตอนวิธีนี้ Y ไม่มีวัฏจักร มีหนึ่งต้นไม้ย่อย และไม่มีต้นไม้สองต้นที่แตกต่างกัน Y ไม่สามารถไม่เชื่อมโยงได้ เพราะ เส้นเชื่อมแรกที่พบจะเชื่อมสองจุดยอดใน Y แล้วจะถูกเพิ่มตามขั้นตอนวิธี ดังนั้น Y จึงเป็นต้นไม้แบบทอดข้ามของ P
ความต่ำสุด[แก้]
เราจะแสดงว่าประพจน์ P เป็นจริงโดยใช้ อุปนัยเชิงคณิตศาสตร์ ถ้า F เป็นเซตของเส้นเชื่อมที่ถูกเลือกที่แต่ละระดับของขั้นตอนวิธี แล้วจะได้ต้นไม้แบบทอดข้ามน้อยที่สุดที่มี F อยู่ด้วย
- ชัดเจนว่า P เป็นจริงตั้งแต่เริ่มต้น เมื่อ F เป็นเซตว่าง ทุกต้นไม้แบบทอดข้ามน้อยที่สุดจะเป็นเช่นนั้น และถ้ามีอย่างน้อยหนึ่งเส้นเชื่อมก็จะเป็นต้นไม้แบบทอดข้ามน้อยที่สุดเพราะเป็นกราฟเชื่อมโยงที่มีน้ำหนัก
- สมมติให้ P เป็นจริงสำหรับบางเซตของเส้นเชื่อม F และให้ T เป็นต้นไม้แบบทอดข้ามน้อยที่สุดที่บรรจุ F ไว้ ถ้าเลือกเส้นเชื่อมถัดไป e ก็ยังอยู่ใน T ดังนั้น P เป็นจริงสำหรับ F + e มิฉะนั้น T + e จะมีวัฏจักร C และเส้นเชื่อมอื่น f ที่อยู่ใน C แต่ไม่อยู่ใน F (ถ้าไม่มีเส้นเชื่อม f เลยแล้ว e จะไม่อยู่เพิ่มเข้าไปใน F เพราะการกระทำนั้นจะทำให้เกิดวัฏจักร C) แล้ว T − f + e เป็นต้นไม้ และมีน้ำหนักเท่ากับ T เพราะ T เป็นมีน้ำหนักน้อยที่สุด และน้ำหนักของ f จะไม่น้อยไปกว่า e มิฉะนั้นขั้นตอนวิธีจะเลือก f แทน e ดังนั้น T − f + e คือต้นไม้แบบทอดข้ามน้อยที่สุด ที่มี F + e
- ดังนั้นจากอุปนัยเชิงคณิตศาสตร์จึงสรุปได้ว่า P เป็นจริง เมื่อ F เป็นต้นไม้ทอดข้าม
ดูเพิ่ม[แก้]
อ้างอิง[แก้]
แหล่งข้อมูลอื่น[แก้]
- Kruskal's algorithm explanation and example with c implementation
- Download the example minimum spanning tree data. เก็บถาวร 2012-07-16 ที่ เวย์แบ็กแมชชีน
- Animation of Kruskal's algorithm (Requires Java plugin)
- download kruskal algorithm Implement with C++ and java(graphical)(Requires java 7+) เก็บถาวร 2013-12-31 ที่ เวย์แบ็กแมชชีน
- C# Implementation
- Open source java graph library with implementation of Kruskal's algorithm
- Auto-generated PowerPoint Slides for Teaching and Learning



