การค้นหาแบบทวิภาค

การค้นหาแบบทวิภาค

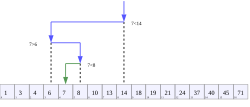ตัวอย่างการค้นหาแบบทวิภาค โดยมี 7 เป็นค่าเป้าหมาย
ประเภท	ขั้นตอนวิธีการค้นหา
โครงสร้างข้อมูล	แถวลำดับ
ประสิทธิภาพเมื่อเกิดกรณีแย่ที่สุด	$O(\log n)$
ประสิทธิภาพเมื่อเกิดกรณีดีที่สุด	$O(1)$
ประสิทธิภาพเมื่อเกิดกรณีทั่วไป	$O(\log n)$
ปริมาณความต้องการพื้นที่เมื่อเกิดกรณีแย่ที่สุด	$O(1)$

ในสาขาวิทยาการคอมพิวเตอร์ การค้นหาแบบทวิภาค (อังกฤษ: binary search, half-interval search หรือ bisection search) เป็นขั้นตอนวิธีเพื่อหาตำแหน่งของค่าที่ต้องการ (ข้อมูลนำเข้า หรือ "key") ที่ใช้ในแถวลำดับที่ได้มีการเรียงลำดับข้อมูลแล้ว ขั้นตอนวิธีจะเริ่มจากเปรียบเทียบข้อมูลที่นำเข้ากับข้อมูลที่อยู่ตรงกลางของแถวลำดับ ถ้าข้อมูลมีค่าเท่ากันแสดงว่าพบ "คีย์" ที่ต้องการ อาจจะทำการคืนค่าตำแหน่งหรือในที่นี้คือ ดัชนี (index) กลับไป มิฉะนั้นถ้าค่าของข้อมูลนำเข้าที่ต้องการค้นหามีการน้อยกว่าค่าตรงกลางของแถวลำดับ ก็จะทำขั้นตอนวิธีนี้อีกครั้งแต่เปลี่ยนมาค้นหาในแถวลำดับย่อยของแถวลำดับที่ต้องการค้นหาโดยแถวลำดับย่อยจะมีจุดสิ้นสุดที่ตรงกลางของแถวลำดับหลัก หรือถ้าข้อมูลที่ต้องการค้นหามีค่ามากกว่าแล้วจะค้นหาในแถวลำดับย่อยเช่นกันแต่ย้ายจุดเริ่มต้นมาที่ตรงกลางของแถวลำดับหลัก เมื่อทำไปจนแถวลำดับไม่มีสมาชิกอยู่หรือจุดเริ่มต้นมากกว่าจุดสิ้นสุด แสดงว่าไม่มีสมาชิกในแถวลำดับตัวใดที่มีค่าเท่ากับข้อมูลนำเข้าที่ต้องการค้นหา อาจจะคืนค่าว่า "ไม่พบ"

ในกรณีแย่ที่สุด การค้นหาแบบทวิภาคจะดำเนินงานโดยมีความซับซ้อนของเวลาในรูปลอการิทึม ซึ่งจะมีค่า $O(\log n)$ เมื่อ $n$ คือจำนวนแถวลำดับของข้อมูล การค้นหาแบบทวิภาคจะใช้เวลาดำเนินงานน้อยกว่าการค้นหาแบบเชิงเส้น ยกเว้นในกรณีที่แถวลำดับมีจำนวนน้อย อย่างไรก็ตาม แถวลำดับนั้นจะต้องมีการเรียงลำดับข้อมูลก่อนจึงจะสามารถดำเนินการค้นหาแบบทวิภาคได้ นอกจากการค้นหาแบบทวิภาคแล้ว ยังมีโครงสร้างข้อมูลเฉพาะแบบอื่น ๆ ที่ถูกออกแบบมาเพื่อให้สามารถค้นหาได้อย่างรวดเร็ว เช่น ตารางแฮช ซึ่งสามารถนำมาใช้ในการค้นหาข้อมูลได้มีประสิทธิภาพกว่าการค้นหาแบบทวิภาค อย่างไรก็ตาม การค้นหาแบบทวิภาคยังคงสามารถใช้แก้ปัญหาได้อย่างกว้างขวาง เช่น การหาข้อมูลที่มีขนาดเล็กที่สุดหรือใหญ่ที่สุดตัวถัดไปในแถวลำดับ ถึงแม้ข้อมูลนั้นจะไม่ปรากฏในแถวลำดับก็ตาม

การค้นหาแบบทวิภาคมีหลากหลายรูปแบบ โดยเฉพาะอย่างยิ่ง การเรียงซ้อนแบบเศษส่วน ที่ช่วยเพิ่มความเร็วในการค้นหาแบบทวิภาคสำหรับข้อมูลที่มีค่าเดียวกันในหลายแถวลำดับ การเรียงซ้อนแบบเศษส่วนช่วยแก้ปัญหาเกี่ยวกับเรขาคณิตเชิงคำนวณ และด้านอื่น ๆ จำนวนมากได้อย่างมีประสิทธิภาพ นอกจากนั้นยังมีการค้นหาแบบเอกซ์โพเนนเชียล ที่ช่วยขยายขอบเขตการค้นหาแบบทวิภาคได้อย่างไม่จำกัด และต้นไม้ค้นหาแบบทวิภาคและต้นไม้แบบบีซึ่งเป็นโครงสร้างข้อมูลที่อ้างอิงมาจากการค้นหาแบบทวิภาค

การค้นหาแบบทวิภาคจะแบ่งครึ่งชุดข้อมูลที่ต้องการค้นหา ดังนั้นจึงจัดให้การค้นหาแบบทวิภาคเป็นขั้นตอนวิธีแบ่งแยกและเอาชนะ และขั้นตอนวิธีการค้นหา

ขั้นตอนวิธี

การค้นหาแบบทวิภาคสามารถดำเนินการได้ในแถวลำดับที่มีการเรียงลำดับข้อมูลแล้ว โดยจะเริ่มจากการเปรียบเทียบค่าของข้อมูลที่อยู่ตรงกลางของแถวลำดับกับค่าเป้าหมาย หากข้อมูลตรงกลางนั้นมีค่าเท่ากับค่าเป้าหมาย จะทำการคืนค่าตำแหน่งในแถวลำดับของข้อมูลนั้น แต่หากข้อมูลตรงกลางมีค่าน้อยกว่าค่าเป้าหมาย การค้นหาแบบทวิภาคจะถูกดำเนินการต่อไปกับแถวลำดับครึ่งหลัง ในทำนองเดียวกัน หากข้อมูลตรงกลางมีค่ามากกว่าค่าเป้าหมาย การค้นหาก็จะถูกดำเนินการในแถวลำดับครึ่งหน้า ด้วยขั้นตอนวิธีนี้ทำให้สามารถกำจัดข้อมูลได้ครึ่งหนึ่งเสมอในทุกการวนซ้ำ

แบบเวียนเกิด

การค้นหาแบบทวิภาคสามารถใช้การเรียกซ้ำได้ โดยมีสิ่งที่ต้องการคือพารามิเตอร์อันได้แก่ แถวลำดับที่มีการเรียงลำดับมาแล้ว (ในต้วอย่างจะเป็นการเรียงลำดับจากน้อยไปมาก) ซึ่งสามารถอ้างถึงแถวลำดับตรงกลางได้ด้วยดัชนี (index) ต้น และปลายของแถวลำดับ ซึ่งพารามิเตอร์เหล่านี้จะทำให้สามารถเรียกฟังก์ชันแบบเรียกซ้ำได้ และโดยขั้นตอนวิธีแล้ว การเขียนการค้นหาแบบทวิภาคด้วยการเวียนเกิดหรือเรียกซ้ำนั้น คอมไพเลอร์จะไม่มีการสร้างกองซ้อนกองใหม่ขึ้นมา โดยจะใช้เพียงกองเดียวเท่านั้น พิจารณาตัวแปร $A$ คือแถวลำดับที่ต้องการค้นหา, $T$ คือค่าของตัวแปรที่ต้องการค้นหาในแถวลำดับ $A$, $L$ คือดัชนีของต้นแถวลำดับ $A$, $R$ คือดัชนีของปลายแถวลำดับ $A$ และ $n$ คือจำนวนแถวลำดับของข้อมูล

function binary_search(A, T, L, R) is
    if L > R then
        return unsuccessful
    else:
        m := floor((L + R) / 2)
        if A[m] < T then
            return binary_search(A, T, m + 1, R)
        else if A[m] > T then
            return binary_search(A, T, L, m - 1)
        else:
            return m

การวนซ้ำ

กำหนดให้แถวลำดับ $A$ มีสมาชิก $n$ ตัว โดยแต่ละตัวมีค่าหรือระเบียน $A_{0},A_{1},A_{2},\ldots ,A_{n-1}$ ซึ่งถูกเรียงลำดับข้อมูลเพื่อให้ $A_{0}\leq A_{1}\leq A_{2}\leq \cdots \leq A_{n-1}$ มีดัชนีของต้นแถวลำดับ $L$ และดัชนีปลายแถวลำดับ $R$ และกำหนดค่าเป้าหมาย $T$ ซับรูทีนต่อไปนี้ใช้การค้นหาแบบทวิภาคเพื่อหาดัชนีตำแหน่งของ $T$ ใน $A$

1. กำหนดให้ $L=0$ และ $R=n-1$
2. ถ้า $L>R$ แล้วการค้นหาจะสิ้นสุดลง และคืนค่าว่าค้นหาไม่สำเร็จ
3. กำหนดให้ $m$ (ตำแหน่งกึ่งกลางของแถวลำดับที่สนใจ) มีค่าเท่ากับฟังก์ชันพื้นของ ${\frac {L+R}{2}}$ หรือหมายถึงจำนวนเต็มที่มากที่สุดที่มีค่าน้อยกว่าหรือเท่ากับ ${\frac {L+R}{2}}$
4. ถ้า $A_{m}<T$ แล้วกำหนดให้ $L=m+1$ และกลับไปยังขั้นตอนที่ 2
5. ถ้า $A_{m}>T$ แล้วกำหนดให้ $R=m-1$ และกลับไปยังขั้นตอนที่ 2
6. ถ้า $A_{m}=T$ แสดงว่าการค้นหาเสร็จสิ้น คืนค่า $m$

ขั้นตอนการวนซ้ำนี้จะติดตามขอบเขตการค้นหาด้วยตัวแปร $L$ และ $R$ และสามารถแสดงผลในรูปรหัสเทียมได้ดังตัวอย่างด้านล่าง โดยชื่อตัวแปรที่ใช้จะคงเดิมเหมือนตัวอย่างด้านบน floor คือ ฟังก์ชันพื้น และ unsuccessful แทนค่าเฉพาะที่สื่อถึงความล้มเหลวของการค้นหา

function binary_search(A, n, T) is
    L := 0
    R := n − 1
    while L ≤ R do
        m := floor((L + R) / 2)
        if A[m] < T then
            L := m + 1
        else if A[m] > T then
            R := m − 1
        else:
            return m
    return unsuccessful

ในอีกทางเลือกหนึ่ง ขั้นตอนวิธีนี้อาจใช้ค่าฟังก์ชันเพดานของ ${\frac {L+R}{2}}$ ซึ่งจะทำให้ผลลัพธ์เปลี่ยนแปลงไปหากค่าเป้าหมายปรากฏในแถวลำดับมากกว่า 1 ครั้ง

ขั้นตอนทางเลือก

ในขั้นตอนวิธีด้านบนอาศัยการตรวจสอบในทุก ๆ การวนซ้ำว่าค่ากลาง ($m$) มีค่าเท่ากับค่าเป้าหมายที่ต้องการ ($T$) หรือไม่ กระบวนการบางอย่างได้ละเว้นวิธีการตรวจสอบนี้ในแต่ละการวนซ้ำ ทำให้ขั้นตอนวิธีนั้นจะทำการตรวจสอบนี้เฉพาะเมื่อการวนซ้ำครั้งนั้นเหลือสมาชิกเพียงตัวเดียว (เมื่อ $L=R$) ส่งผลให้ใช้เวลาน้อยลงในระหว่างรอบการวนซ้ำ เนื่องจากชุดเปรียบเทียบจะถูกกำจัดทิ้งหนึ่งชุดในหนึ่งรอบการวนซ้ำ ในขณะที่มีจำนวนรอบการวนซ้ำเพิ่มขึ้นเพียงหนึ่งครั้งโดยเฉลี่ยเท่านั้น

Hermann Bottenbruch ได้ตีพิมพ์กระบวนการแรกที่ละเว้นวิธีการตรวจสอบนี้ในปีค.ศ. 1962

1. กำหนดให้ $L=0$ และ $R=n-1$
2. เมื่อ $L\neq R$
   1. กำหนดให้ $m$ (ตำแหน่งกึ่งกลางของแถวลำดับที่สนใจ) มีค่าเท่ากับฟังก์ชันเพดานของ ${\frac {L+R}{2}}$ หรือหมายถึงจำนวนเต็มที่น้อยที่สุดที่มีค่ามากกว่าหรือเท่ากับ ${\frac {L+R}{2}}$
   2. ถ้า $A_{m}>T$ แล้วกำหนดให้ $R=m-1$
   3. มิฉะนั้น ถ้า $A_{m}\leq T$ แล้วกำหนดให้ $L=m$
3. เมื่อ $L=R$ การค้นหาจะเสร็จสิ้นลง ถ้า $A_{L}=T$ แล้วจะคืนค่า $L$ มิฉะนั้นจะคืนค่าว่าไม่สำเร็จ

เมื่อ ceil คือฟังก์ชันเพดาน รหัสเทียมของกระบวนการนี้ คือ:

function binary_search_alternative(A, n, T) is
    L := 0
    R := n − 1
    while L != R do
        m := ceil((L + R) / 2)
        if A[m] > T then
            R := m − 1
        else:
            L := m
    if A[L] = T then
        return L
    return unsuccessful

สมาชิกที่ซ้ำกัน

การค้นหาแบบทวิภาคอาจคืนค่าดัชนีใด ๆ ของสมาชิกที่มีค่าเท่ากับค่าเป้าหมาย ถึงแม้ในแถวลำดับจะมีสมาชิกที่มีค่าซ้ำกัน ยกตัวอย่างเช่น ถ้าแถวลำดับที่ต้องการค้นหาคือ $[1,2,3,4,4,5,6,7]$ และค่าเป้าหมายคือ $4$ แล้วขั้นตอนวิธีอาจคืนค่าที่ถูกต้องได้ทั้งตำแหน่งที่ 4 (ดัชนีที่ 3) หรือตำแหน่งที่ 5 (ดัชนีที่ 4) ซึ่งกระบวนการปกติมักจะคืนค่าตำแหน่งที่ 4 (ดัชนีที่ 3) แต่ก็ไม่ใช่เสมอไปที่ค่าที่ถูกคืนจะเป็นตำแหน่งแรกของสมาชิกที่ซ้ำกัน อย่างไรก็ตาม ในบางครั้งการหาค่าเป้าหมายที่มีสมาชิกที่ซ้ำกันในแถวลำดับก็จำเป็นที่จะต้องหาสมาชิกขอบซ้ายสุดหรือขวาสุด ในตัวอย่างข้างต้น สมาชิกซ้ายสุดที่มีค่าเท่ากับ 4 คือสมาชิกตำแหน่งที่ 4 และสมาชิกขวาสุดที่มีค่าเท่ากับ 4 คือสมาชิกตำแหน่งที่ 5 ซึ่งการค้นหาโดยใช้ขั้นตอนทางเลือกจะคืนค่าดัชนีของสมาชิกขวาสุด (ถ้ามี)

กระบวนการหาสมาชิกซ้ายสุด

ในการจะหาสมาชิกซ้ายสุดสามารถทำได้ดังนี้:

1. กำหนดให้ $L=0$ และ $R=n$
2. เมื่อ $L<R$
   1. กำหนดให้ $m$ (ตำแหน่งกึ่งกลางของแถวลำดับที่สนใจ) มีค่าเท่ากับฟังก์ชันพื้นของ ${\frac {L+R}{2}}$ หรือหมายถึงจำนวนเต็มที่มากที่สุดที่มีค่าน้อยกว่าหรือเท่ากับ ${\frac {L+R}{2}}$
   2. ถ้า $A_{m}<T$ แล้วกำหนดให้ $L=m+1$
   3. มิฉะนั้น ถ้า $A_{m}\geq T$ แล้วกำหนดให้ $R=m$
3. คืนค่า $L$

ถ้า $L<n$ และ $A_{L}=T$ แล้ว $A_{L}$ คือสมาชิกซ้ายสุดที่มีค่าเท่ากับ $T$ ในกรณีที่ไม่มีสมาชิกใดในแถวลำดับที่มีค่าเท่ากับ $T$ $L$ จะถือว่าเป็นอันดับของ $T$ ในแถวลำดับ หรือคือจำนวนสมาชิกทั้งหมดในแถวลำดับที่มีค่าน้อยกว่า $T$

เมื่อ floor คือฟังก์ชันพื้น รหัสเทียมของกระบวนการนี้ คือ:

function binary_search_leftmost(A, n, T):
    L := 0
    R := n
    while L < R:
        m := floor((L + R) / 2)
        if A[m] < T:
            L := m + 1
        else:
            R := m
    return L

กระบวนการหาสมาชิกขวาสุด

ในการจะหาสมาชิกขวาสุดสามารถทำได้ดังนี้:

1. กำหนดให้ $L=0$ และ $R=n$
2. เมื่อ $L<R$
   1. กำหนดให้ $m$ (ตำแหน่งกึ่งกลางของแถวลำดับที่สนใจ) มีค่าเท่ากับฟังก์ชันพื้นของ ${\frac {L+R}{2}}$ หรือหมายถึงจำนวนเต็มที่มากที่สุดที่มีค่าน้อยกว่าหรือเท่ากับ ${\frac {L+R}{2}}$
   2. ถ้า $A_{m}>T$ แล้วกำหนดให้ $R=m$
   3. มิฉะนั้น ถ้า $A_{m}\leq T$ แล้วกำหนดให้ $L=m+1$
3. คืนค่า $R-1$

ถ้า $R>0$ และ $A_{R}-1=T$ แล้ว $A_{R}-1$ คือสมาชิกขวาสุดที่มีค่าเท่ากับ $T$ ในกรณีที่ไม่มีสมาชิกใดในแถวลำดับที่มีค่าเท่ากับ $T$ $n-R$ จะเป็นจำนวนสมาชิกทั้งหมดในแถวลำดับที่มีค่ามากกว่ากว่า $T$

เมื่อ floor คือฟังก์ชันพื้น รหัสเทียมของกระบวนการนี้ คือ:

function binary_search_rightmost(A, n, T):
    L := 0
    R := n
    while L < R:
        m := floor((L + R) / 2)
        if A[m] > T:
            R := m
        else:
            L := m + 1
    return R - 1

การหาคู่ที่ใกล้เคียง

การค้นหาแบบทวิภาคสามารถปรับปรุงเพื่อคำนวณหาคู่ที่ใกล้เคียงได้ ในตัวอย่างด้านบน อันดับ (rank) สมาชิกก่อนหน้า (predecessor) สมาชิกตามหลัง (successor) และเพื่อนบ้านใกล้สุด (nearest neighbor) ได้ถูกแสดงสำหรับค่าเป้าหมายเท่ากับ $5$ ซึ่งไม่อยู่ในแถวลำดับนี้

กระบวนการด้านต้นจะดำเนินการหาคู่ที่ถูกต้องซึ่งคือตำแหน่งของสมาชิกที่มีค่าเท่ากับค่าเป้าหมายเท่านั้น อย่างไรก็ตาม การขยายขอบเขตการค้นหาแบบทวิภาคเพื่อดำเนินการหาคู่ที่ใกล้เคียงก็สามารถทำได้โดยง่าย เพราะการค้นหาแบบทวิภาคจะดำเนินการในแถวลำดับที่เรียงลำดับแล้ว ยกตัวอย่างเช่น การค้นหาแบบทวิภาคสามารถใช้เพื่อคำนวณอันดับ (จำนวนสมาชิกที่มีค่าน้อยกว่า) สมาชิกก่อนหน้า (predecessor) สมาชิกตามหลัง (successor) และเพื่อนบ้านใกล้สุดของค่าที่กำหนด ซึ่งการหาขอบเขตหรือคือการหาจำนวนสมาชิกระหว่างค่าสองค่าก็สามารถดำเนินการได้ด้วยการหาอันดับ 2 ครั้ง

• การหาอันดับสามารถดำเนินการได้ด้วยกระบวนการหาสมาชิกซ้ายสุด โดยจะคืนค่าจำนวนสมาชิกที่มีค่าน้อยกว่าค่าเป้าหมาย
• การหาสมาชิกก่อนหน้าสามารถดำเนินการได้ด้วยการหาอันดับ ถ้าอันดับของค่าเป้าหมายคือ $r$ แล้วอันดับของสมาชิกก่อนหน้าคือ $r-1$
• การหาสมาชิกตามหลังสามารถดำเนินการได้ด้วยกระบวนการหาสมาชิกขวาสุด ถ้ากระบวนการนั้นคืนค่า $r$ แล้วอันดับของสมาชิกตามหลังคือ $r+1$
• เพื่อนบ้านใกล้สุดของค่าเป้าหมายอาจเป็นสมาชิกก่อนหน้าหรือสมาชิกตามหลังก็ได้ ขึ้นอยู่กับว่าค่าไหนใกล้เคียงค่าเป้าหมายมากกว่ากัน
• การหาขอบเขตสามารถทำได้อย่างตรงไปตรงมา โดยเมื่อรู้อันดับของค่าทั้งสอง (สมาชิกก่อนหน้าและสมาชิกตามหลัง) แล้ว จำนวนสมาชิกที่มีค่ามากกว่าหรือเท่ากับค่าสมาชิกก่อนหน้าและน้อยกว่าค่าสมาชิกตามหลังจะเป็นผลต่างระหว่างอันดับของค่าทั้งสอง การนับแบบนี้สามารถมีค่าเพิ่มขึ้นหรือลดลง 1 ค่าได้ขึ้นอยู่กับว่าจุดปลายของขอบเขตควรถูกพิจารณาเป็นส่วนหนึ่งของขอบเขตหรือไม่ และแถวลำดับมีข้อมูลที่เข้าคู่กับจุดปลายเหล่านั้นหรือไม่

ประสิทธิภาพ

A ต้นไม้แสดงถึงการค้นหาแบบทวิภาค แถวลำดับที่กำลังถูกค้นหาอยู่คือ $[20,30,40,50,80,90,100]$ และค่าเป้าหมายคือ $40$.

กรณีที่แย่ที่สุดจะเกิดขึ้นเมื่อการค้นหาดำเนินการไปถึงชั้นล่างสุดของต้นไม้ ในขณะที่กรณีที่ดีที่สุดจะเกิดขึ้นเมื่อค่าเป้าหมายคือค่ากลางของแถวลำดับ

ในแง่ของจำนวนการเปรียบเทียบ ประสิทธิภาพของการค้นหาแบบทวิภาคสามารถวิเคราะห์ได้จากการดูการทำงานของต้นไม้แบบทวิภาค โดยปมรากของต้นไม้คือค่ากลางของแถวลำดับ ค่ากลางของครึ่งแถวล่างคือปมลูกด้านซ้ายของราก และค่ากลางของครึ่งแถวบนคือปมลูกด้านขวาของราก ส่วนที่เหลือของต้นไม้ก็มีโครงสร้างที่คล้ายคลึงกับรูปแบบที่กล่าวไปด้านต้น คือ เริ่มจากปมราก การตัดสินใจว่าจะผ่านต้นไม้ย่อยด้านซ้ายหรือขวาจะขึ้นอยู่กับว่า ค่าเป้าหมายมีค่าน้อยหรือมากกว่าปมที่กำลังตัดสินใจอยู่

ในกรณีที่แย่ที่สุด การค้นหาแบบทวิภาคจะถูกวนซ้ำทั้งหมด ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ รอบการเปรียบเทียบ เมื่อ ${\textstyle \lfloor \rfloor }$ คือสัญลักษณ์ที่แสดงถึงฟังก์ชันพื้นที่ให้ผลลัพธ์เป็นจำนวนเต็มที่มากที่สุดที่น้อยกว่าหรือเท่ากับอาร์กิวเมนต์ (argument) และ ${\textstyle \log _{2}}$ คือลอการิทึมฐานสอง เนื่องจากกรณีที่แย่ที่สุดจะเกิดขึ้นเมื่อการค้นหาดำเนินการไปถึงชั้นล่างสุดของต้นไม้ ซึ่งต้นไม้แบบทวิภาคจะมีทั้งหมด ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ ชั้นเสมอ

กรณีที่แย่ที่สุดอาจเกิดขึ้นได้เช่นกันในกรณีที่ค่าเป้าหมายไม่อยู่ในแถวลำดับ ถ้า ${\textstyle n}$ มีค่าน้อยกว่ากำลังของสองอยู่หนึ่งค่า แล้วกรณีนี้จะเป็นจริงเสมอ มิฉะนั้น การค้นหาอาจวนซ้ำ ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ รอบเมื่อการค้นหาดำเนินการไปถึงชั้นล่างสุดของต้นไม้ อย่างไรก็ตาม หากการค้นหาสิ้นสุดที่ชั้นที่ลึกที่สุดเป็นอันดับสองของต้นไม้ แล้วการค้นหาจะวนซ้ำทั้งหมด ${\textstyle \lfloor \log _{2}(n)\rfloor }$ รอบ ซึ่งน้อยกว่าจำนวนการวนซ้ำของกรณีที่แย่ที่สุดอยู่หนึ่งครั้ง

หากสมมุติให้สมาชิกทุกตัวมีโอกาสที่จะถูกค้นหาเท่ากัน แล้วการค้นหาแบบทวิภาคจะวนซ้ำทั้งหมด $\lfloor \log _{2}(n)\rfloor +1-(2^{\lfloor \log _{2}(n)\rfloor +1}-\lfloor \log _{2}(n)\rfloor -2)/n$ รอบโดยเฉลี่ย เมื่อค่าเป้าหมายมีอยู่ในแถวลำดับ ซึ่งจะประมาณเท่ากับ $\log _{2}(n)-1$ รอบ ถ้าค่าเป้าหมายไม่อยู่ในแถวลำดับ แล้วการค้นหาแบบทวิภาคจะวนซ้ำ $\lfloor \log _{2}(n)\rfloor +2-2^{\lfloor \log _{2}(n)\rfloor +1}/(n+1)$ รอบโดยเฉลี่ย โดยสมมุติให้ขอบเขตระหว่างและนอกเหนือจากสมาชิกมีโอกาสที่จะถูกค้นหาเท่ากัน

ในกรณีที่ดีที่สุด หรือเมื่อค่าเป้าหมายคือค่ากลางของแถวลำดับ ตำแหน่งของค่าเป้าหมายจะถูกคืนค่าหลังจากการวนซ้ำเพียงหนึ่งรอบ

ในแง่ของการวนซ้ำ ไม่มีขั้นตอนวิธีการค้นหาใดที่ทำการค้นหาโดยการเปรียบเทียบสมาชิกในแถวลำดับแล้วจะมีประสิทธิภาพทั้งในกรณีเฉลี่ยและกรณีที่แย่ที่สุดดีกว่าการค้นหาแบบทวิภาค ต้นไม้ตัดสินใจแสดงให้เห็นว่าการค้นหาแบบทวิภาคมีจำนวนชั้นน้อยที่สุดเท่าที่จะเป็นไปได้เมื่อจำนวนชั้นที่อยู่สูงกว่าชั้นล่างสุดทั้งหมดของต้นไม้ถูกเติมเต็มหมดแล้ว มิฉะนั้น ขั้นตอนวิธีการค้นหาสามารถกำจัดสมาชิกในหนึ่งการวนซ้ำได้เล็กน้อย ซึ่งจะเป็นการเพิ่มจำนวนการวนซ้ำที่จำเป็นทั้งในกรณีเฉลี่ยและกรณีที่แย่ที่สุด และนั่นจะเป็นกรณีสำหรับขั้นตอนวิธีการค้นหาแบบอื่น ๆ ที่อาศัยการเปรียบเทียบสมาชิก ถึงแม้ว่าขั้นตอนวิธีการค้นหาอื่นอาจดำเนินการได้เร็วกว่าสำหรับค่าเป้าหมายบางค่า แต่ประสิทธิภาพโดยเฉลี่ยก็ยังคงน้อยกว่าการค้นหาแบบทวิภาค เนื่องจากการค้นหาแบบทวิภาคจะมีการแบ่งครึ่งแถวลำดับเสมอ ดังนั้นจึงจะมั่นใจได้ว่าขนาดของแถวลำดับย่อยที่ถูกแบ่งทั้งสองแถวจะมีค่าใกล้เคียงกันมากที่สุด อย่างไรก็ตาม การค้นหาแบบทวิภาคจะสามารถดำเนินการได้ในแถวลำดับที่มีการเรียงลำดับแล้วเท่านั้น

ความซับซ้อนด้านพื้นที่

การค้นหาแบบทวิภาคจำเป็นต้องใช้พอยน์เตอร์ (pointer) 3 อันในการเก็บตำแหน่งที่อยู่ของตัวแปร โดยอาจเป็นดัชนีของแถวลำดับ หรือพอยน์เตอร์ไปยังตำแหน่งที่อยู่หน่วยความจำ โดยไม่คำนึงถึงขนาดของแถวลำดับ ดังนั้น ความซับซ้อนด้านพื้นที่ของการค้นหาแบบทวิภาคคือ $O(1)$ ในรูปแบบการคำนวณ word RAM

แหล่งที่มาของกรณีเฉลี่ย

จำนวนการวนซ้ำโดยเฉลี่ยของการค้นหาแบบทวิภาคขึ้นอยู่กับความน่าจะเป็นที่สมาชิกแต่ละตัวในแถวลำดับจะถูกค้นหา กรณีเฉลี่ยจะแตกต่างกันไปสำหรับการค้นหาที่สำเร็จและไม่สำเร็จ สำหรับการค้นหาที่สำเร็จจะถูกอนุมานว่าสมาชิกแต่ละตัวในแถวลำดับมีโอกาสที่จะถูกค้นหาเท่ากัน สำหรับการค้นหาที่ไม่สำเร็จจะถูกอนุมานว่าช่วงระหว่างและนอกเหนือจากสมาชิกมีโอกาสที่จะถูกค้นหาเท่ากัน กรณีเฉลี่ยสำหรับการค้นที่สำเร็จคือจำนวนการวนซ้ำเพื่อค้นหาสมาชิกทุกตัวในครั้งเดียว หารด้วย $n$ ซึ่งก็คือจำนวนสมาชิกในแถวลำดับ ส่วนกรณีเฉลี่ยสำหรับการค้นหาที่ไม่สำเร็จคือจำนวนการวนซ้ำเพื่อค้นหาสมาชิกในทุกช่วงในครั้งเดียว หารด้วยจำนวน $n+1$ ช่วง

การค้าหาที่สำเร็จ

ในต้นไม้แบบทวิภาค การค้นหาที่สำเร็จสามารถถูกอธิบายได้ด้วยเส้นทางจากรากถึงปมเป้าหมาย เรียกว่า เส้นทางภายใน (internal path) ความยาวของเส้นทางจะเท่ากับจำนวนขอบ (เส้นเชื่อมต่อระหว่างปม) ที่เส้นทางเดินทางผ่าน เมื่อกำหนดให้เส้นทางที่สอดคล้องนั้นมีความยาว $l$ จำนวนการวนซ้ำในการค้นจะเท่ากับ $l+1$ โดยนับการวนซ้ำรอบแรกด้วย ความยาวของเส้นทางภายในจะเท่ากับผลรวมของความยาวของเส้นทางภายในที่เฉพาะ เนื่องจากจะมีเพียงหนึ่งเส้นทางที่เดินทางจากรากไปยังปมเดี่ยวใด ๆ ดังนั้น เส้นทางภายในแต่ละเส้นจะเป็นตัวแทนของการค้นหาสมาชิกแต่ละตัวโดยเฉพาะ ถ้ามีสมาชิกทั้งหมด $n$ ตัว (ซึ่ง $n$ จะเป็นจำนวนเต็มบวก) และความยาวของเส้นทางภายในคือ $I(n)$ แล้วจำนวนการวนซ้ำโดยเฉลี่ยสำหรับการค้นหาที่สำเร็จคือ $T(n)=1+{\frac {I(n)}{n}}$ โดยจำนวนการวนซ้ำ 1 ครั้งที่ถูกบวกเข้าไปเพิ่มคือการวนซ้ำครั้งแรก

เนื่องจากการค้นหาแบบทวิภาคคือขั้นตอนวิธีที่ดีที่สุดในการค้นหาแบบเปรียบเทียบ ปัญหานี้จะถูกลดลงเหลือเพียงการคำนวณความยาวของเส้นทางภายในที่น้อยที่สุดของต้นไม้แบบทวิภาคทั้งหมดที่มีปม $n$ ปม ซึ่งจะเท่ากับ:

$I(n)=\sum _{k=1}^{n}\left\lfloor \log _{2}(k)\right\rfloor$

ตัวอย่างเช่น ในแถวลำดับที่มีสมาชิก 7 ตัว หากค่าเป้าหมายคือราก การค้นหาจะต้องใช้การวนซ้ำหนึ่งครั้ง หากเป็นสมาชิกที่อยู่ล่างรากหนึ่งชั้นจะต้องใช้การวนซ้ำสองครั้ง และสมาชิกสี่ตัวล่างสุดจะต้องใช้การวนซ้ำสามครั้ง ในกรณีนี้ ความยาวของเส้นทางภายในคือ:

$\sum _{k=1}^{7}\left\lfloor \log _{2}(k)\right\rfloor =0+2(1)+4(2)=2+8=10$

จากสมการการคำนวณกรณีเฉลี่ย จำนวนการวนซ้ำโดยเฉลี่ยจะเท่ากับ $1+{\frac {10}{7}}=2{\frac {3}{7}}$ และผลรวม $I(n)$ สามารถเขียนให้อยู่ในรูปอย่างง่ายได้ดังนี้:

$I(n)=\sum _{k=1}^{n}\left\lfloor \log _{2}(k)\right\rfloor =(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2$

แทนค่าสมการ $I(n)$ ในสมการ $T(n)$:

$T(n)=1+{\frac {(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2}{n}}=\lfloor \log _{2}(n)\rfloor +1-(2^{\lfloor \log _{2}(n)\rfloor +1}-\lfloor \log _{2}(n)\rfloor -2)/n$

สำหรับจำนวนเต็ม $n$ สมการด้านบนนี้คือสมการของกรณีเฉลี่ยสำหรับการค้นหาที่สำเร็จ

การค้าหาที่ไม่สำเร็จ

การค้นหาที่ไม่สำเร็จสามารถถูกอธิบายได้โดยการแผ่ขยายต้นไม้ด้วยปมภายนอก (external nodes) ซึ่งจะเกิดเป็นต้นไม้ทวิภาคแบบแผ่ขยาย (extended binary tree) ถ้าปมภายในหรือปมที่ปรากฏในต้นไม้มีปมลูกน้อยกว่า 2 ปม แล้วปมลูกเพิ่มเติมหรือปมภายนอกจะถูกเพิ่มในต้นไม้เพื่อให้ปมภายในแต่ละปมมีปมลูกครบ 2 ปม ด้วยวิธีการนี้แล้วจะทำให้การค้นหาที่ไม่สำเร็จสามารถถูกอธิบายได้ด้วยเส้นทางไปยังปมภายนอกที่มีพ่อแม่เป็นปมเดี่ยวเดียวที่มีอยู่ในการวนซ้ำครั้งสุดท้าย เส้นทางภายนอกคือเส้นทางจากรากสู่ปมภายนอก ซึ่งความยาวของเส้นทางภายนอกนั้นจะเท่ากับผลรวมของความยาวของเส้นทางภายนอกที่เฉพาะ ถ้ามีสมาชิกทั้งหมด $n$ ตัว (ซึ่ง $n$ จะเป็นจำนวนเต็มบวก) และความยาวของเส้นทางภายนอกคือ $E(n)$ แล้วจำนวนการวนซ้ำโดยเฉลี่ยสำหรับการค้นหาที่ไม่สำเร็จคือ $T'(n)={\frac {E(n)}{n+1}}$ โดยจำนวนการวนซ้ำ 1 ครั้งที่ถูกบวกเข้าไปเพิ่มคือการวนซ้ำครั้งแรก สมการความยาวของเส้นทางภายนอกถูกหารด้วย $n+1$ แทนที่จะเป็น $n$ เพราะมีเส้นทางภายนอกทั้งหมด $n+1$ เส้น ซึ่งคือช่วงระหว่างและนอกเหนือจากสมาชิกในแถวลำดับ

เช่นเดียวกับการค้นหาที่สำเร็จ ปัญหานี้จะถูกลดลงเหลือเพียงการคำนวณความยาวของเส้นทางภายนอกที่น้อยที่สุดของต้นไม้แบบทวิภาคทั้งหมดที่มีปม $n$ ปม สำหรับต้นไม้แบบทวิภาคทั้งหมด ความยาวของเส้นทางภายนอกเท่ากับความยาวของเส้นทางภายในบวกด้วย $2n$ แทนค่าสมการ $I(n)$:

$E(n)=I(n)+2n=\left[(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2\right]+2n=(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}$

แทนค่าสมการ $E(n)$ ในสมการ $T'(n)$ สมการของกรณีเฉลี่ยสำหรับการค้นหาที่ไม่สำเร็จคือ:

$T'(n)={\frac {(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}}{(n+1)}}=\lfloor \log _{2}(n)\rfloor +2-2^{\lfloor \log _{2}(n)\rfloor +1}/(n+1)$

ประสิทธิภาพของขั้นตอนทางเลือก

ในการวนซ้ำแต่ละครั้งของขั้นตอนการค้นหาแบบทวิภาคด้านบนจะมีการเปรียบเทียบหนึ่งหรือสองครั้ง คือการเปรียบเทียบว่าค่าตรงกลางเท่ากับค่าเป้าหมายหรือไม่ในแต่ละการวนซ้ำ สมมุติให้สมาชิกแต่ละตัวในแถวลำดับมีโอกาสที่จะถูกค้นหาเท่ากัน การวนซ้ำแต่ละครั้งจะมีการเปรียบเทียบทั้งหมด 1.5 ครั้งโดยเฉลี่ย ตัวแปรของขั้นตอนวิธีจะตรวจสอบว่าค่าตรงกลางมีค่าเท่ากับค่าเป้าหมายหรือไม่ในตอนท้ายของการค้นหา ซึ่งทำให้ตัวเปรียบเทียบถูกกำจัดทิ้งไปครึ่งหนึ่งโดยเฉลี่ยในแต่ละการวนซ้ำ สิ่งนี้จะช่วยลดเวลาที่ใช้ในการค้นหาต่อจำนวนการวนซ้ำหนึ่งรอบในคอมพิวเตอร์ส่วนมาก อย่างไรก็ตาม การค้นหานี้จะมีจำนวนการวนซ้ำมากที่สุดอย่างแน่นอน โดยเฉลี่ยแล้วจำนวนการวนซ้ำจะเพิ่มขึ้นหนึ่งครั้ง แต่เนื่องจากการวนเปรียบเทียบจะทำทั้งหมด ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ ครั้งในกรณีที่แย่ที่สุด ประสิทธิภาพที่เพิ่มขึ้นเล็กน้อยในแต่ละการวนซ้ำจึงไม่สามารถทดแทนจำนวนการวนซ้ำที่เพิ่มขึ้นได้ (ยกเว้นในกรณีที่ $n$ มีค่ามาก ๆ)

ระยะเวลาดำเนินการและแคชที่ใช้ (Running time and cache use)

ในการวิเคราะห์ประสิทธิภาพของการค้นหาแบบทวิภาคจะต้องพิจารณาระยะเวลาที่ใช้ในการเปรียบเทียบสมาชิกสองตัว สำหรับจำนวนเต็มและสตริง (string) ระยะเวลาที่ใช้ในการดำเนินการจะเพิ่มขึ้นแปรผันตรงกับความยาวของการเข้ารหัสสมาชิกหรือก็คือจำนวนบิตของสมาชิก ตัวอย่างเช่น การเปรียบเทียบคู่ของจำนวนเต็มเฉพาะค่าบวกขนาด 64 บิทจะอาศัยการเปรียบเทียบเป็นสองเท่าของการเปรียบเทียบคู่ของจำนวนเต็มเฉพาะค่าบวกขนาด 32 บิท กรณีที่แย่ที่สุดจะเกิดขึ้นเมื่อจำนวนเต็มทั้งสองมีค่าเท่ากัน ซึ่งระยะเวลาดำเนินการนี้จะยิ่งมากอย่างมีนัยสำคัญเมื่อความยาวของการเข้ารหัสสมาชิกมีค่ามาก เช่น การเปรียบเทียบข้อมูลชนิดจำนวนเต็มขนาดใหญ่หรือสตริงแบบยาว ซึ่งจะทำให้การเปรียบเทียบข้อมูลมีราคาแพง นอกจากนั้น การเปรียบเทียบค่าของจำนวนจุดลอยตัว (การแทนจำนวนจริงแบบดิจิทัลที่พบเห็นบ่อยที่สุด) จะแพงกว่าการเปรียบเทียบจำนวนเต็มและสตริงแบบสั้น

ในสถาปัตยกรรมคอมพิวเตอร์ส่วนมาก หน่วยประมวลผลกลางจะมีแคชของฮาร์ดแวร์แยกจากแรม เนื่องจากอยู่ในหน่วยประมวลผลกลาง แคชจะเข้าถึงได้รวดเร็วกว่าแต่ก็กักเก็บข้อมูลได้น้อยกว่าแรม ดังนั้น หน่วยประมวลผลกลางส่วนมากจะกักเก็บตำแหน่งหน่วยความจำ (memory location) ที่ถูกเข้าถึงเมื่อไม่นานมานี้และที่อยู่ใกล้เคียงกัน ยกตัวอย่างเช่น เมื่อเข้าถึงสมาชิกของแถวลำดับ สมาชิกนั้นอาจถูกกักเก็บควบคู่ไปกับสมาชิกที่อยู่ใกล้เคียงกับมันในแรม ทำให้สามารถเข้าถึงสมาชิกที่มีดัชนีใกล้เคียงกัน (locality of reference) ได้อย่างรวดเร็ว ในแถวลำดับที่มีการเรียงลำดับแล้ว การค้นหาแบบทวิภาคสามารถกระโดดไปยังตำแหน่งหน่วยความจำที่อยู่ไกลได้ถ้าแถวลำดับนั้นมีขนาดใหญ่ ต่างจากขั้นตอนวิธีอื่น เช่น การค้นหาเชิงเส้น และการตรวจสอบเชิงเส้นในตารางแฮช ซึ่งเข้าถึงสมาชิกได้ตามลำดับเท่านั้น ในระบบส่วนใหญ่ สิ่งนี้อาจเพิ่มระยะเวลาดำเนินการของการค้นหาแบบทวิภาคในแถวลำดับขนาดใหญ่ได้เล็กน้อย

การค้าหาแบบทวิภาคเปรียบเทียบกับการค้นหาแบบอื่น ๆ

การใช้การค้นหาแบบทวิภาคในการดำเนินการเพิ่มและลบสมาชิกในแถวลำดับที่มีการเรียงลำดับไว้แล้วนับเป็นวิธีการที่ไม่มีประสิทธิภาพ เนื่องจากใช้เวลาถึง $O(n)$ ในการดำเนินการแต่ละครั้ง นอกจากนั้นแล้ว แถวลำดับที่มีการเรียงลำดับแล้วยังมีการใช้หน่วยความจำที่ซับซ้อน โดยเฉพาะเมื่อสมาชิกถูกเพิ่มเข้าไปในแถวลำดับบ่อย ๆ ดังนั้นจึงมีโครงสร้างข้อมูลอื่น ๆ ที่สามารถดำเนินการเพิ่มและลบได้มีประสิทธิภาพมากกว่า การค้นหาแบบทวิภาคสามารถใช้เพื่อการดำเนินการหาคู่ที่ถูกต้องและการตรวจสอบการเป็นสมาชิกของเซต (ตรวจสอบว่าค่าเป้าหมายอยู่ในกลุ่มสมาชิกข้อมูลหรือไม่) ซึ่งถึงแม้โครงสร้างข้อมูลอื่น ๆ จะสามารถดำเนินการหาคู่ที่ถูกต้องและตรวจสอบการเป็นสมาชิกของเซตได้รวดเร็วกว่าการค้นหาแบบทวิภาค แต่การค้นหาแบบทวิภาคสามารถใช้หาคู่ที่ใกล้เคียงได้อย่างมีประสิทธภาพในขณะที่การค้นหาแบบอื่น ๆ ไม่สามารถทำได้ ซึ่งการค้นหาแบบทวิภาคใช้เวลา ${\textstyle O(\log n)}$ โดยไม่คำนึงถึงชนิดของโครงสร้างข้อมูล นอกจากนั้น ยังมีการดำเนินการบางอย่าง เช่น การหาค่าที่มากและน้อยที่สุด ที่สามารถดำเนินการได้อย่างมีประสิทธิภาพในแถวลำดับที่มีการเรียงลำดับแล้ว

การค้นหาเชิงเส้น

การค้นหาเชิงเส้นเป็นขั้นตอนวิธีการค้นหาที่เรียบง่าย โดยจะใช้วิธีการตรวจสอบข้อมูลทุก ๆ ตัวจนกว่าจะเจอค่าเป้าหมาย การค้นหาเชิงเส้นสามารถทำได้ในรายการโยง (linked list) ซึ่งสามารถดำเนินการเพิ่มหรือลบสมาชิกได้รวดเร็วกว่าแถวลำดับ การค้นหาแบบทวิภาคดำเนินการการค้นหาในแถวลำดับได้รวดเร็วกว่าการค้นหาเชิงเส้น (ยกเว้นแถวลำดับที่มีขนาดสั้น) แต่แถวลำดับนั้นจะต้องมีการเรียงลำดับมาก่อน ขั้นตอนวิธีการเรียงลำดับทั้งหมดมีพื้นฐานมาจากการเปรียบเทียบค่าของสมาชิก เช่น ควิกซอร์ต และการเรียงลำดับแบบผสาน ซึ่งใช้การเปรียบเทียบทั้งหมด ${\textstyle O(n\log n)}$ ในกรณีที่แย่ที่สุด การค้นหาแบบทวิภาคสามารถใช้หาคู่ที่ใกล้เคียงได้อย่างมีประสิทธภาพในขณะที่การค้นหาเชิงเส้นไม่สามารถทำได้ นอกจากนั้น การดำเนินการ เช่น การหาสมาชิกที่มีค่ามากและน้อยที่สุด สามารถทำได้อย่างมีประสิทธิภาพในแถวลำดับที่มีการเรียงลำดับแล้วเท่านั้น

ต้นไม้

ต้นไม้ค้นหาแบบทวิภาคถูกใช้ในการค้นหาด้วยขั้นตอนวิธีที่คล้ายกับการค้นหาแบบทวิภาค

ต้นไม้ค้นหาแบบทวิภาค คือโครงสร้างข้อมูลต้นไม้แบบทวิภาคที่มีการดำเนินการโดยอาศัยหลักการของการค้นหาแบบทวิภาค ระเบียนในต้นไม้สามารถถูกค้นหาได้โดยใช้ขั้นตอนวิธีที่คล้ายกับการค้นหาแบบทวิภาค โดยใช้เวลาโดยเฉลี่ยในรูปฟังก์ชันอัลกอริทึม การเพิ่มและลบข้อมูลในต้นไม้ค้นหาแบบทวิภาคก็ใช้เวลาโดยเฉลี่ยในรูปฟังก์ชันอัลกอริทึมเช่นเดียวกัน ซึ่งวิธีนี้จะใช้เวลาน้อยกว่าเวลาในรูปแบบเชิงเส้นที่ใช้ในการเพิ่มหรือลบข้อมูลในแถวลำดับที่มีการเรียงลำดับแล้ว และต้นไม้แบบทวิภาคยังสามารถดำเนินการทุกอย่างได้เหมือนกับที่สามารถทำในแถวลำดับที่มีการเรียงลำดับแล้ว รวมไปถึงการหาขอบเขตและค่าที่ใกล้เคียง

อย่างไรก็ตาม ต้นไม้ค้นหาแบบทวิภาคมักจะมีความไม่สมดุลระหว่างสองข้าง ทำให้มีประสิทธิภาพในการค้นหาน้อยกว่าการค้นหาแบบทวิภาคเล็กน้อย สิ่งนี้ยังนำไปใช้ได้กับต้นไม้ค้นหาแบบทวิภาคที่มีโครงสร้างปรับสมดุลเองได้ หรือคือต้นไม้ค้นหาแบบทวิภาคที่สามารถทำให้ปมของตนเองมีความสมดุลได้ เพราะ ต้นไม้ที่มีจำนวนชั้นน้อยที่สุดเท่าที่จะเป็นไปได้แทบจะไม่ถูกสร้างขึ้นมาเลย นอกเหนือจากต้นไม้ค้นหาแบบทวิภาคที่มีโครงสร้างปรับสมดุลเองได้แล้ว ต้นไม้มักจะมีความไม่สมดุลอย่างรุนแรงเนื่องจากมีจำนวนปมภายในที่มีปมลูกครบสองปมน้อยมาก ทำให้ระยะเวลาในการค้นหาโดยเฉลี่ยและในกรณีที่แย่ที่สุดใกล้เคียงกับเวลาที่ใช้ในกรณีที่มีการเปรียบเทียบ $n$ ครั้ง นอกจากนั้นต้นไม้ค้นหาแบบทวิภาคยังใช้พื้นที่เก็บข้อมูลมากกว่าแถวลำดับที่เรียงลำดับแล้ว

ต้นไม้ค้นหาแบบทวิภาคจะยืมหน่วยความจำภายนอกของฮาร์ดดิสก์เพื่อใช้ในการค้นหาแบบรวดเร็วเนื่องจากต้นไม้ค้นหาแบบทวิภาคสามารถจัดโครงสร้างในระบบแฟ้มข้อมูลได้ ซึ่งต้นไม้แบบบีคือการสรุปวิธีการการจัดระเบียบต้นไม้นี้ โดยต้นไม้แบบบีมักถูกใช้ในการจัดระเบียบพื้นที่จัดเก็บข้อมูลระยะยาว เช่น ฐานข้อมูล และแฟ้มข้อมูล

แฮชชิง

โดยปกติแล้วสำหรับการใช้แถวลำดับแบบจับคู่ ตารางแฮช ซึ่งคือโครงสร้างข้อมูลที่เชื่อมโยงคีย์กับระเบียนโดยใช้ฟังก์ชันแฮช จะสามารถนำแถวลำดับแบบจับคู่ไปใช้ได้รวดเร็วกว่าการค้นหาแบบทวิภาคในแถวลำดับระเบียนที่มีการเรียงลำดับแล้ว การใช้ตารางแฮชส่วนมากใช้เวลาโดยเฉลี่ยแบบถัวเฉลี่ย อย่างไรก็ตาม แฮชชิงไม่สามารถใช้ในการหาคู่ที่ใกล้เคียง เช่น การคำนวณหาค่าที่น้อยที่สุดตัวถัดไป ค่าที่มากที่สุดตัวถัดไป และคีย์ที่ใกล้เคียงที่สุดได้ เนื่องจากหากการค้นหาไม่สำเร็จจะมีการคืนค่าได้เพียงว่าค่าเป้าหมายนั้นไม่มีอยู่ในระเบียนใด ๆ ดังนั้น การค้นหาแบบทวิภาคจึงถือเป็นวิธีการที่ดีที่สุดสำหรับการหาคู่ประเภทนั้น เนื่องจากใช้เวลาในรูปฟังก์ชันลอการิทึมเท่านั้น นอกจากนั้น การดำเนินการบางอย่าง เช่น การหาสมาชิกที่มีค่ามากหรือน้อยที่สุด สามารถทำได้อย่างมีประสิทธิภาพในแถวลำดับที่มีการเรียงลำดับแล้ว แต่ไม่สามารถทำได้ในตารางแฮช

ขั้นตอนวิธีการตรวจสอบการเป็นสมาชิกของเซต

ปัญหาที่เกี่ยวข้องกับการค้นหาคือ การตรวจสอบการเป็นสมาชิกของเซต ขั้นตอนวิธีที่มีฟังก์ชันการค้นหา เช่น การค้นหาแบบทวิภาค สามารถนำมาใช้ในการตรวจสอบการเป็นสมาชิกของเซตได้ นอกจาการค้นหาแบบทวิภาคแล้วยังมีขั้นตอนวิธีอื่น ๆ ที่เหมาะสมกับการตรวจสอบการเป็นสมาชิกของเซตโดยเฉพาะมากกว่า แถวลำดับบิต คือโครงสร้างข้อมูลที่เรียบง่ายและเป็นประโยชน์ดีสุดเมื่อขอบเขตของคีย์มีจำกัด โดยแถวลำดับบิตจะเก็บข้อมูลโดยใช้พื้นที่น้อยที่สุดในรูปแบบของบิต ซึ่งบิตแต่ละตัวก็จะเป็นตัวแทนของคีย์แต่ละตัวในขอบเขตของคีย์ แถวลำดับบิตมีการดำเนินการที่รวดเร็วมาก โดยใช้เวลาเพียง $O(1)$ เท่านั้น นอกจากแถวลำดับบิตแล้ว Judy1 ของแถวลำดับจูดี้ก็ยังสามารถจัดเก็บคีย์ขนาด 64 บิตได้อย่างมีประสิทธิภาพ

สำหรับผลลัพธ์ที่ใกล้เคียง ตัวกรองของบลูม หรือคือโครงสร้างข้อมูลที่เกี่ยวกับความเป็นไปได้ซึ่งอาศัยการแฮชชิง จะกักเก็บเซตของคีย์โดยการเข้ารหัสคีย์ซึ่งจะอาศัยแถวลำดับบิต และฟังก์ชันแฮชหลายฟังก์ชัน ส่วนมากแล้ว ตัวกรองของบลูมจะใช้พื้นที่กักเก็บข้อมูลน้อยกว่าแถวลำดับบิตในขณะที่ก็ใช้เวลาดำเนินการไม่ได้นานกว่า โดยหากอาศัยฟังก์ชันแฮชทั้งหมด $k$ ฟังก์ชัน การตรวจสอบการเป็นสมาชิกของเซตจะใช้เวลาดำเนินการเพียง $O(k)$ เท่านั้น อย่างไรก็ตาม ตัวกรองของบลูมยังคงมีปัญหาเรื่องผลบวกลวงอยู่

โครงสร้างข้อมูลอื่น ๆ

ยังมีโครงสร้างข้อมูลอื่น ๆ อีกที่มีการปรับปรุงจากการค้นหาแบบทวิภาคทั้งในด้านการค้นหาและการดำเนินการอื่น ๆ ที่สามารถทำได้ในแถวลำดับที่มีการเรียงลำดับแล้ว ตัวอย่างเช่น โครงสร้างข้อมูลแบบเฉพาะด้าน เช่น Van Emde Boas tree ต้นไม้ฟิวชัน และแถวลำดับบิต สามารถดำเนินการค้นหา การหาคู่ที่ใกล้เคียง และการดำเนินการอื่น ๆ ที่สามารถทำได้ในแถวลำดับที่มีการเรียงลำดับแล้ว ได้อย่างมีประสิทธิภาพมากกว่าการค้นหาแบบทวิภาค โครงสร้างข้อมูลแบบเฉพาะด้านเหล่านี้สามารถดำเนินการได้รวดเร็วกว่า เพราะใช้ประโยชน์จากคุณสมบัติของคีย์ที่มีแอททริบิวต์ (attribute) บางอย่าง (โดยปกติจะเป็นคีย์ที่เป็นจำนวนเต็มที่มีขนาดเล็ก) ดังนั้นสำหรับคีย์ที่ไม่มีแอททริบิวต์เหล่านั้นก็จะทำให้ใช้เวลาและพื้นที่จัดเก็บข้อมูลมากขึ้น ตราบใดที่คีย์นั้นสามารถจัดลำดับได้ การดำเนินการเหล่านี้ก็สามารถดำเนินการได้โดยไม่ต้องคำนึงถึงคีย์ ซึ่งจะมีประสิทธิภาพอย่างต่ำเทียบเท่ากับประสิทธิภาพในแถวลำดับที่มีการเรียงลำดับไว้แล้ว โครงสร้างข้อมูลบางอย่าง เช่น แถวลำดับจูดี้ สามารถใช้วิธีการหลายอย่างร่วมกันเพื่อลดปัญหาที่ได้กล่าวไปในขณะที่ก็ยังคงประสิทธิภาพและความสามารถในการดำเนินการหาคู่ที่ใกล้เคียงไว้อยู่

การค้นหาแบบอื่น ๆ

การค้นหาแบบทวิภาคอย่างมีเอกรูป

บทความหลัก: การค้นหาแบบทวิภาคอย่างมีเอกรูป

การค้นหาแบบทวิภาคอย่างมีเอกรูปจะกักเก็บผลต่างระหว่างดัชนีของค่ากลางปัจจุบันและค่ากลางสองตัวต่อไปในการวนซ้ำครั้งหน้าไว้แทนค่าขอบเขต

การค้นหาแบบทวิภาคอย่างมีเอกรูปจะเก็บค่าผลต่างระหว่างดัชนีของค่ากลางในการวนซ้ำครั้งปัจจุบันและดัชนีของค่ากลางในการวนซ้ำครั้งต่อไป ซึ่งต่างจากการค้นหาแบบทวิภาคที่เก็บค่าดัชนีของขอบเขตบนและล่าง โดยตารางค้นหา ที่เก็บค่าผลต่างนี้จะถูกคำนวณไว้ล่วงหน้า ตัวอย่างเช่น ถ้าแถวลำดับที่กำลังถูกค้นหาคือ [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11] แล้วค่ากลาง ($m$) คือ 6 ในขณะที่ค่ากลางของแถวลำดับย่อยฝั่งซ้ายหรือ ([1, 2, 3, 4, 5]) คือ 3 และค่ากลางของแถวลำดับย่อยฝั่งขวาหรือ ([7, 8, 9, 10, 11]) คือ 9 การค้นหาแบบทวิภาคอย่างมีเอกรูปจะเก็บค่า 3 เนื่องจากดัชนีค่ากลางตัวต่อไปทั้งสองต่างก็มีผลต่างกับ 6 เท่ากัน เพื่อที่จะลดพื้นที่ที่ใช้ในการค้นหา ขั้นตอนวิธีจะบวกหรือลบผลต่างดังกล่าวจากดัชนีของค่ากลางตัวปัจจุบัน การค้นหาแบบทวิภาคอย่างมีเอกรูปอาจดำเนินการได้รวดเร็วเมื่อถูกใช้ในระบบที่ไม่สามารถคำนวณค่ากลางได้อย่างมีประสิทธิภาพนัก เช่น ในคอมพิวเตอร์แบบทศนิยม

การค้นหาแบบเอกซ์โพเนนเชียล

บทความหลัก: Exponential search

ภาพการจำลองการค้นหาแบบเอกซ์โพเนนเชียลในขั้นตอนการหาขอบเขตบนเพื่อใช้สำหรับการค้นหาแบบทวิภาคในภายหลัง

การค้นหาแบบเอกซ์โพเนนเชียลขยายขอบเขตจากการค้นหาแบบทวิภาคทำให้สามารถดำเนินการได้ในรายการที่ไม่จำกัดขอบเขต โดยจะเริ่มต้นจากการค้นหาสมาชิกตัวแรกที่ดัชนีอยู่ในรูปกำลังของสองและมีค่ามากกว่าค่าเป้าหมาย จากนั้นจึงกำหนดดัชนีของค่านั้นให้เป็นขอบเขตบน และเริ่มดำเนินการค้นหาแบบทวิภาค การค้นหาสมาชิกตัวแรกที่ตรงตามเงื่อนไขจะมีการวนซ้ำทั้งหมด ${\textstyle \lfloor \log _{2}x+1\rfloor }$ ครั้ง ก่อนที่จะเริ่มการค้นหาแบบทวิภาคซึ่งจะมีการวนซ้ำสูงสุด ${\textstyle \lfloor \log _{2}x\rfloor }$ ครั้ง เมื่อ $x$ คือตำแหน่งของค่าเป้าหมาย การค้นหาแบบเอกซ์โพเนนเชียลสามารถทำงานได้ในรายการที่มีการจำกัดขอบเขตเช่นกัน แต่จะมีประสิทธิภาพดีกว่าการค้นหาแบบทวิภาคก็ต่อเมื่อค่าเป้าหมายอยู่ใกล้กับบริเวณเริ่มต้นของแถวลำดับ

การค้นหาโดยการประมาณช่วง

บทความหลัก: การค้นหาโดยการประมาณช่วง

ภาพการจำลองการค้นหาโดยการประมาณช่วงโดยใช้การประมาณค่าในช่วงเชิงเส้น โดยในตัวอย่างนี้ไม่จำเป็นต้องมีการค้นหาเพิ่มเพราะการประมาณตำแหน่งของเป้าหมายในแถวลำดับนั้นถูกต้องแล้ว การนำไปใช้อื่น ๆ อาจมีการใช้ฟังก์ชันอื่นในการประมาณตำแหน่งของเป้าหมาย

การค้นหาโดยการประมาณช่วงใช้การประมาณตำแหน่งของค่าเป้าหมายโดยพิจารณาจากสมาชิกที่มีค่าสูงสุดและต่ำสุดในแถวลำดับ และขนาดของแถวลำดับ แตกต่างจากการค้นหาแบบก่อนหน้าที่ใช้การคำนวณค่ากลางเป็นหลัก เนื่องจากอาศัยหลักการที่ว่า ค่ากลางมักไม่ใช่การคาดการณ์ที่ดีที่สุดในหลายกรณีที่เป็นไปได้ เช่น ในกรณีที่ค่าเป้าหมายอยู่ใกล้เคียงกับค่าปลายสุดของแถวลำดับ

ฟังก์ชันการประมาณช่วงที่นิยมใช้กัน คือ การประมาณค่าในช่วงเชิงเส้น กำหนดให้ $A$ คือแถวลำดับ $L,R$ คือขอบเขตล่างและขอบเขตบนตามลำดับ และ $T$ คือค่าเป้าหมาย จะได้ว่าค่าเป้าหมายจะอยู่ห่างจาก $L$ และ $R$ เป็นระยะประมาณ $(T-A_{L})/(A_{R}-A_{L})$ เมื่อใช้การประมาณค่าในช่วงเชิงเส้นในแถวลำดับที่มีการแจกแจงของสมาชิกแบบเอกรูปหรือใกล้เคียงกับเอกรูป การค้นหาโดยการประมาณช่วงจะทำการเปรียบเทียบทั้งหมด ${\textstyle O(\log \log n)}$ ครั้ง

ในการทำงานจริง การค้นหาโดยการประมาณช่วงจะดำเนินการช้ากว่าการค้นหาแบบทวิภาคในแถวลำดับที่มีขนาดเล็ก เนื่องจากการค้นหาโดยการประมาณช่วงจะต้องมีการคำนวณเพิ่มเติม แต่เมื่อขนาดแถวลำดับเพิ่มขึ้น อัตราการเพิ่มขึ้นของความซับซ้อนของเวลาในการค้นหาโดยการประมาณช่วงจะช้ากว่าการค้นหาแบบทวิภาค อย่างไรก็ตาม สิ่งนี้สามารถชดเชยได้ในกรณีที่แถวลำดับมีขนาดใหญ่มากเท่านั้น

การเรียงซ้อนแบบเศษส่วน

ในการเรียงซ้อนแบบเศษส่วน แถวลำดับแต่ละตัวจะมีพอยน์เตอร์ที่ชี้ไปยังสมาชิกทุกตัวของแถวลำดับต่อไป ดังนั้นจึงใช้การค้นหาแบบทวิภาคเพียงหนึ่งครั้งในการค้นหาในทุกแถวลำดับ

การเรียงซ้อนแบบเศษส่วน คือเทคนิคที่ใช้ในการเพิ่มความเร็วในการค้นหาแบบทวิภาคสำหรับข้อมูลที่มีค่าเดียวกันในหลายแถวลำดับที่มีการเรียงลำดับแล้ว การค้นหาแยกกันในแต่ละแถวลำดับจะใช้เวลา ${\textstyle O(k\log n)}$ เมื่อ $k$ คือจำนวนแถวลำดับทั้งหมด การเรียงซ้อนแบบเศษส่วนจะลดเวลาการดำเนินการนั้นเหลือเพียง ${\textstyle O(k+\log n)}$ โดยอาศัยการเก็บข้อมูลเกี่ยวกับสมาชิกแต่ละตัวและตำแหน่งของมันในแถวลำดับอื่นลงไปในแถวลำดับแต่ละอัน

แต่เดิม การเรียงซ้อนแบบเศษส่วนถูกพัฒนามาเพื่อแก้ปัญหาเกี่ยวกับเรขาคณิตเชิงคำนวณได้อย่างมีประสิทธิภาพ ปัจจุบันการเรียงซ้อนแบบเศษส่วนยังถูกนำไปประยุกต์ใช้ในด้านอื่น ๆ อีก เช่น ในการทำเหมืองข้อมูล และในอินเทอร์เน็ตโพรโทคอล

การประยุกต์ใช้ในกราฟ

การค้นหาแบบทวิภาคถูกนำมาใช้กับกราฟบางประเภท โดยค่าเป้าหมายนั้นจะถูกเก็บในรูปของโหนดแทนสมาชิกในแถวลำดับ ต้นไม้ค้นหาแบบทวิภาคคือหนึ่งในตัวอย่างนั้น เมื่อโหนดของต้นไม้ถูกตรวจสอบ ขั้นตอนวิธีจะได้รู้ว่าโหนดนั้นคือเป้าหมายหรือไม่ หรือค่าเป้าหมายจะอยู่ในต้นไม้ย่อยต้นไหน อย่างไรก็ตาม การค้นหาแบบทวิภาคสามารถนำไปใช้ได้ในกราฟอื่นได้อีก เช่น ในกราฟแบบไม่มีทิศทางและถ่วงน้ำหนักเชิงบวก (an undirected, positively weighted graph) ขั้นตอนวิธีจะทราบจากการตรวจสอบโหนดใด ๆ ว่า โหนดนั้นมีค่าเท่ากับค่าเป้าหมายหรือไม่ ถ้าไม่แล้วเส้นเชื่อม (incident edge) ใดที่เป็นเส้นทางที่สั้นที่สุดจากโหนดที่กำลังตรวจสอบอยู่ไปยังโหนดเป้าหมาย เช่นเดียวกัน ต้นไม้ค้นหาแบบทวิภาคจะพิจารณาเส้นเชื่อมไปยังต้นไม้ย่อยฝั่งซ้ายและฝั่งขวาเมื่อโหนดที่กำลังตรวจสอบอยู่มีค่าไม่เท่ากับค่าเป้าหมาย สำหรับกราฟแบบไม่มีทิศทางและถ่วงน้ำหนักเชิงบวกทุกกราฟ ในกรณีที่แย่ที่สุด ขั้นตอนวิธีจะใช้การตรวจสอบทั้งหมด $O(\log n)$ ครั้งจนกว่าจะเจอโหนดเป้าหมาย

Noisy binary search

ใน noisy binary search มีความน่าจะเป็นที่การเปรียบเทียบนั้นจะให้ผลลัพธ์ที่ไม่ถูกต้อง

ขั้นตอนวิธีของ Noisy binary search ถูกใช้แก้ปัญหาในกรณีที่ขั้นตอนวิธีไม่สามารถเปรียบเทียบค่าของสมาชิกในแถวลำดับได้อย่างน่าเชื่อถือ ในการเปรียบเทียบแต่ละคู่สมาชิกนั้นมีโอกาสที่ขั้นตอนวิธีจะเปรียบเทียบได้ผลลัพธ์ที่ไม่ถูกต้อง Noisy binary search สามารถค้นหาตำแหน่งที่ถูกต้องของเป้าหมายได้โดยมีความน่าจะเป็นที่ควบคุมความน่าเชื่อถือของผลลัพธ์ที่ได้ ทุก ๆ Noisy binary search จะต้องมีการเปรียบเทียบอย่างน้อย $(1-\tau ){\frac {\log _{2}(n)}{H(p)}}-{\frac {10}{H(p)}}$ ครั้งโดยเฉลี่ย โดยที่ $H(p)=-p\log _{2}(p)-(1-p)\log _{2}(1-p)$ คือ binary entropy function และ $\tau$ คือ ความน่าจะเป็นที่กระบวนการนั้นจะคืนค่าตำแหน่งเป้าหมายที่ไม่ถูกต้อง ปัญหา noisy binary search เช่น เกมของอุลาม คือการถามคำถามยี่สิบข้อที่แตกต่างกันเพื่อทายวัตถุหรือตัวเลขนั้น โดยคำตอบที่ได้รับจากคำถามนั้นอาจไม่ถูกต้อง

การค้นหาแบบทวิภาคควอนตัม

การดำเนินการค้นหาแบบทวิภาคในคอมพิวเตอร์แบบดั้งเดิมจะใช้การวนซ้ำทั้งหมด ${\textstyle \lfloor \log _{2}n+1\rfloor }$ ครั้งในกรณีที่แย่ที่สุด ขั้นตอนวิธีควอนตัมสำหรับการค้นหาแบบทวิภาคจะมีการตรวจสอบทั้งหมด ${\textstyle \log _{2}n}$ ครั้ง (แทนจำนวนการวนซ้ำในกระบวนการดั้งเดิม) แต่ตัวประกอบคงที่ (constant factor) จะมีค่าน้อยกว่าหนึ่ง ทำให้มีค่าความซับซ้อนของเวลาน้อยลงเมื่อทำงานในคอมพิวเตอร์เชิงควอนตัม กระบวนการของการค้นหาแบบทวิภาคควอนตัมที่แท้จริง หรือคือกระบวนการที่จะคืนค่าผลลัพธ์ที่ถูกต้องเสมอ จะต้องมีการตรวจสอบอย่างน้อย ${\textstyle {\frac {1}{\pi }}(\ln n-1)\approx 0.22\log _{2}n}$ ครั้งในกรณีที่แย่ที่สุด เมื่อ ${\textstyle \ln }$ คือ ลอการิทึมธรรมชาติ กระบวนการของการค้นหาแบบทวิภาคควอนตัมที่แท้จริงบางอันดำเนินการตรวจสอบทั้งหมด ${\textstyle 4\log _{605}n\approx 0.433\log _{2}n}$ ครั้งในกรณีที่แย่ที่สุด ในทางตรงกันข้าม ขั้นตอนวิธีของโกรเวอร์ คือขั้นตอนวิธีควอนตัมที่ดีที่สุดสำหรับการค้นหาสมาชิกในรายการแบบไม่มีลำดับ โดยใช้การตรวจสอบทั้งหมด $O({\sqrt {n}})$ ครั้ง

การใช้ในงานทั่วไป

การค้นหาในข้อมูลที่มีการเรียงลำดับแล้วในงานทั่วไป เช่น พจนานุกรมที่มีการเรียงรายการของคำและความหมาย ถ้ารู้คำเราก็จะสามารถหาความหมายได้, สมุดโทรศัพท์ที่มีการเรียงลำดับรายการชื่อ, ที่อยู่ และเบอร์โทรศัพท์ หากรู้ชื่อก็จะหาเบอร์โทรศัพท์และที่อยู่ได้อย่างรวดเร็ว

ถ้ารายการที่ได้ค้นหามีข้อมูลเล็กน้อยเช่น 1 โหล การค้นหาแบบทวิภาคจะใช่เวลาเพียงเล็กน้อยเมื่อเปรียบเทียบกับการค้นหาแบบเชิงเส้น แต่มันต้องการรายการที่มีการเรียงลำดับมาแล้ว คล้ายกับตารางแฮชหรือการค้นหาแบบแฮชที่มีความเร็วมากกว่าการค้นหาแบบทวิภาคแต่ยังมีลักษณะของข้อมูลที่ค่อนข้างเจาะจงกว่าด้วยเช่นกัน ถ้ารู้ว่าต้องทำการค้นหาเป็นจำนวนหลายครั้งหรือลักษณะของข้อมูลตรงกับที่ต้องการแล้วควรเลือกใช้การค้นหาแบบทวิภาค แต่ถ้าต้องค้นหาเพียงไม่ก็ครั้งหรือเพียงครั้งเดียวการเลือกใช้การค้นหาแบบเชิงเส้นก็น่าจะเป็นตัวเลือกที่ดีที่สุด

ตัวอย่าง

เกมเดาตัวเลข

นี่คือเกมพื้นฐานที่ใช้หลักการเดียวกันกับขั้นตอนวิธีนี้โดยเริ่มจากคำพูดว่า "ผมกำหนดจำนวนเต็มหนึ่งจำนวนที่มีค่าระหว่าง 40 ถึง 60 และเพื่อที่คุณจะเดาได้ ผมจะบอกว่า 'มากกว่า', 'น้อยกว่า' หรือ 'ใช่!' เมื่อคำตอบถูกต้อง" การค้นหาข้อมูลจำนวน "N" ข้อมูลที่เป็นไปได้ดังนั้นมากกว่า $\lfloor \log _{2}N\rfloor$ คำถามที่ต้องถาม หรือกล่าวง่ายๆว่าเกมจะต้องกำหนดจำนวนคำถามมากกว่า $\lfloor \log _{2}N\rfloor$ คำถาม เมื่อมีการถามแต่ละครั้งพื้นที่ในการค้นหาแต่ละครั้งก็จะถูกแบ่งครึ่งไปเรื่อยๆ ดังนั้นจำนวนการค้นหาจึงถูกบีบให้อยู่ในช่วงๆหนึ่ง แม้ว่าจำนวนที่จะเดามีขนาดใหญ่ก็ตาม, ในกรณีที่ไม่มีขอบเขตบนก็จะสามารถค้นหาได้ที่ประสิทธิภาพ $2\lfloor \log _{2}k\rfloor +1$ เริ่มด้วยหาขอบเขตบนโดยการเพิ่มค่าที่เดาซ้ำแล้วซ้ำอีก ตัวอย่างเช่น คำตอบคือ 11 โดยจะเดาเป็นแบบรูปดังนี้ 1(มากกว่า), 2(มากกว่า), 4(มากกว่า), 8(มากกว่า), 16(น้อยกว่า), 12(น้อยกว่า), 10(มากกว่า) และนี่เรารู้ว่าจำนวนนั้นคือ 11 เพราะเป็นจำนวนที่มากกว่า 10 และน้อยกว่า 12 ถ้าลองใช้วิธีการนี้กับจำนวนเต็มลบและศูนย์บ้าง เช่น จะหา −13: 0, −1, −2, −4, −8, −16, −12, −14 ในที่สุดแล้วก็จะรู้ว่าเลขที่ต้องการคือ -13 เพราะเป็นเลขที่น้อยกว่า -12 และมากกว่า -14

รายการของคำ

ในการค้นหาทั่วไปมีการใช้การค้นหาแบบทวิภาคและการค้นหาแบบสอดแทรกโดยที่ไม่รู้ตัว เมื่อจะหารายชื่อของบุคคลในสมุดโทรศัพท์ เราต้องเริ่มด้วยการเดาจนเมื่อเรารู้ว่ารายการที่กำลังค้นหานั้นได้มีการเรียงลำดับแล้ว นั่นทำให้เราสามารถค้นหารายชื่อที่ต้องการได้อย่างรวดเร็ว เช่น ถ้าจะหาชื่อ "สมชาย" แต่ถ้าเราเปิดไปเจอหน้าที่มีชื่อ "ศรราม" เราก็จะพลิกไปหน้าถัดๆไปที่เราคะเนไว้ว่าจะมีชื่อที่ต้องการ หากหน้าที่พริกไปนั่นมีชื่อ "องอาจ" ดังนั้นจะสรุปได้ว่ารายชื่อของ "สมชาย" ก็จะอยู่ระหว่างหน้าของ "ศรราม" กับ "องอาจ" ซึ่งขั้นตอนดังกล่าวจะทำให้เราแบ่งปัญหาให้เป็นปัญหาย่อยได้

คลังโปรแกรม

คลังโปรแกรมที่รองรับและพร้อมใช้ในภาษาคอมพิวเตอร์ต่างๆ มีดังต่อไปนี้

ดูเพิ่ม

• วิธีแบ่งครึ่ง

เชิงอรรถและอ้างอิง

บรรณานุกรม

• Bentley, Jon (2000). Programming pearls (2nd ed.). Addison-Wesley. ISBN 978-0-201-65788-3.
• Butterfield, Andrew; Ngondi, Gerard E. (2016). A dictionary of computer science (7th ed.). Oxford, UK: Oxford University Press. ISBN 978-0-19-968897-5.
• Chang, Shi-Kuo (2003). Data structures and algorithms. Software Engineering and Knowledge Engineering. Vol. 13. Singapore: World Scientific. ISBN 978-981-238-348-8.
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009). Introduction to algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 978-0-262-03384-8.
• Fitzgerald, Michael (2015). Ruby pocket reference. Sebastopol, California: O'Reilly Media. ISBN 978-1-4919-2601-7.
• Goldman, Sally A.; Goldman, Kenneth J. (2008). A practical guide to data structures and algorithms using Java. Boca Raton, Florida: CRC Press. ISBN 978-1-58488-455-2.
• Kasahara, Masahiro; Morishita, Shinichi (2006). Large-scale genome sequence processing. London, UK: Imperial College Press. ISBN 978-1-86094-635-6.
• Knuth, Donald (1997). Fundamental algorithms. The Art of Computer Programming. Vol. 1 (3rd ed.). Reading, MA: Addison-Wesley Professional. ISBN 978-0-201-89683-1.
• Knuth, Donald (1998). Sorting and searching. The Art of Computer Programming. Vol. 3 (2nd ed.). Reading, MA: Addison-Wesley Professional. ISBN 978-0-201-89685-5.
• Knuth, Donald (2011). Combinatorial algorithms. The Art of Computer Programming. Vol. 4A (1st ed.). Reading, MA: Addison-Wesley Professional. ISBN 978-0-201-03804-0.
• Moffat, Alistair; Turpin, Andrew (2002). Compression and coding algorithms. Hamburg, Germany: Kluwer Academic Publishers. doi:10.1007/978-1-4615-0935-6. ISBN 978-0-7923-7668-2.
• Sedgewick, Robert; Wayne, Kevin (2011). Algorithms (4th ed.). Upper Saddle River, New Jersey: Addison-Wesley Professional. ISBN 978-0-321-57351-3. Condensed web version ; book version .
• Stroustrup, Bjarne (2013). The C++ programming language (4th ed.). Upper Saddle River, New Jersey: Addison-Wesley Professional. ISBN 978-0-321-56384-2.

แหล่งข้อมูลอื่น

• NIST Dictionary of Algorithms and Data Structures: binary search
• Comparisons and benchmarks of a variety of binary search implementations in C