1 + 2 + 3 + 4 + ⋯
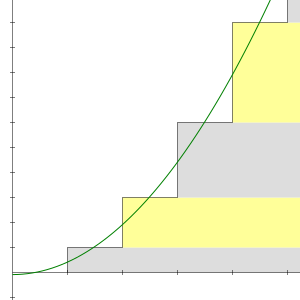
ผลบวกของทุกจำนวนธรรมชาติ 1 + 2 + 3 + 4 + ⋯ เป็นอนุกรมลู่ออก ผลบวกย่อยที่ n ของอนุกรมเป็นจำนวนสามเหลี่ยม
ซึ่งเพิ่มขึ้นอย่างไม่มีขอบเขต โดย n เป็นอนันต์ เนื่องจากลำดับของผลบวกย่อยไม่ลู่เข้าลิมิตจำกัดค่าหนึ่ง อนุกรมดังกล่าวจึงลู่ออก และไม่มีผลบวกในความหมายทั่วไป
แม้ว่าอนุกรมนี้ไม่มีค่าที่มีความหมายใด ๆ เมื่อแรกเห็น แต่อนุกรมนี้สามารถเปลี่ยนรูปให้ผลลัพธ์ที่น่าสนใจทางคณิตศาสตร์ ซึ่งบางผลลัพธ์นั้นมีการใช้ในสาขาอื่น เช่น การวิเคราะห์เชิงซ้อน ทฤษฎีสนามควอนตัมและทฤษฎีสตริง มีการใช้วิธีการรวมยอดจำนวนมากในวิชาคณิตศาสตร์เพื่อกำหนดค่าตัวเลขให้แม้แต่กับอนุกรมลู่ออก โดยเฉพาะอย่างยิ่ง วิธีการทำให้ปรกติของฟังก์ชันซีตา (zeta function regularization) และการรวมยอดรามานุจันกำหนดให้อนุกรมมีค่า −1/12 ซึ่งแสดงโดยสูตรอันขึ้นชื่อ[1]
ในเอกสารเฉพาะเรื่องว่าด้วยทฤษฎีแสงจันทร์ (moonshine theory) เทอร์รี แกนนอนเรียกสมการนี้ว่า "หนึ่งในสูตรที่สะดุดตาที่สุดของวิทยาศาสตร์"[2]
ผลบวกบางส่วน[แก้]

ผลบวกบางส่วนของอนุกรม 1 + 2 + 3 + 4 + 5 + ⋯ คือ 1, 3, 6, 10, 15 ฯลฯ ผลบวกที่ n หาได้จากสูตรง่าย ๆ
พีทาโกรัสและศิษย์ (Pythagorean) อาจทราบสมการดังกล่าวตั้งแต่ศตวรรษที่ 6 ก่อนคริสตกาล[3] จำนวนในรูปนี้เรียก จำนวนสามเหลี่ยม เพราะสามารถจัดจำนวนเหล่านี้เป็นสามเหลี่ยมได้
ลำดับอจำนวนสามเหลี่ยมอนันต์ลู่ออกเป็น +∞ ฉะนั้นโดยบทนิยาม อนุกรมอนันต์ 1 + 2 + 3 + 4 + ⋯ จึงลู่ออกเป็น +∞ เช่นกัน การลู่ออกเป็นผลอย่างง่ายของอนุกรมรูปแบบนี้ พจน์ไม่เข้าใกล้ศูนย์ ฉะนั้นอนุกรมจึงลู่ออกโดยการทดสอบพจน์
การรวมยอดได้[แก้]

ในบรรดาอนุกรมลู่ออกคลาสสิก 1 + 2 + 3 + 4 + · · · นั้นจัดรูปให้เป็นค่าจำกัดได้ค่อนข้างยาก มีการใช้วิธีการรวมยอดจำนวนมากเพื่อให้ค่าจำนวนแก่อนุกรมลู่ออก ซึ่งบางวิธีทรงพลัง (powerful) กว่าวิธีอื่น ตัวอย่างเช่น การรวมยอดเซซาโรซึ่งใช้หาผลบวกของอนุกรมแกรนดี (อนุกรมลู่ออก 1 − 1 + 1 − 1 + ⋯) เป็น 1/2 การรวมยอดอะเบลเป็นวิธีทรงพลังกว่าซึ่งไม่เพียงหาผลบวกของอนุกรมแกรนดีเป็น 1/2 เท่านั้น แต่ยังหาผลบวกของอนุกรมที่ซับซ้อนกว่า 1 − 2 + 3 − 4 + · · · เป็น 1/4 ด้วย
1 + 2 + 3 + 4 + · · · แตกต่างจากสองอนุกรมข้างต้น คือ ไม่สามารถรวมได้ด้วยการรวมยอดเซซาโรหรืออะเบล วิธีเหล่านั้นใช้ได้กับอนุกรมลู่ออกที่แกว่งกวัด แต่ไม่สามารถให้คำตอบจำกัดแก่อนุกรมที่ลู่ออกสู่ +∞ ได้[4] บทนิยามที่มูลฐานกว่าของผลบวกอนุกรมลู่ออกส่วนใหญ่เสถียรและเป็นเชิงเส้น และวิธีการใดที่ทั้งเสถียรและเป็นเชิงเส้นไม่สามารถหาผลบวกของ 1 + 2 + 3 +... เป็นค่าจำกัดได้ จึงจำเป็นต้องใช้วิธีการขั้นสูงกว่านั้น เช่น การทำให้ปรกติของฟังก์ชันซีตาหรือการรวมยอดรามานุจัน นอกจากนี้การสนับสนุนค่า −1/12 โดยใช้วิทยาการศึกษาสำนึกอย่างหยาบ ๆ ซึ่งสัมพันธ์กับวิธีเหล่านี้ยังเป็นไปได้ด้วย
ศรีนิวาสะ รามานุจันนำเสนอการแปลง "1 + 2 + 3 + 4 + ⋯ = −1/12" สองแบบในบทที่ 8 ของสมุดบันทึกเล่มแรกของเขา[5][6][7] การแปลงแบบง่ายและเคร่งครัดน้อยกว่ามีสองขั้นตอน ดังนี้
วิจารณญาณสำคัญอย่างแรก คือ อนุกรมจำนวนบวก 1 + 2 + 3 + 4 + · · · คล้ายกับอนุกรมสลับ 1 − 2 + 3 − 4 + · · · ซึ่งอนุกรมที่สองนี้ก็เป็นอนุกรมลู่ออกเช่นกัน แต่สามารถเปลี่ยนรูปได้ง่ายกว่า มีวิธีคลาสสิกหลายวิธีที่กำหนดค่าให้กับอนุกรมนี้ ซึ่งได้มีการสำรวจตั้งแต่คริสต์ศตวรรษที่ 18[8]
ในการแปลงอนุกรม 1 + 2 + 3 + 4 + · · · เป็น 1 − 2 + 3 − 4 + · · · สามารถลบ 4 จากพจน์ที่สอง 8 จากพจน์ที่สี่ 12 จากพจน์ที่หกไปเรื่อย ๆ จำนวนรวมที่จะถูกนำมาลบเป็น 4 + 8 + 12 + 16 + · · · ซึ่งเป็น 4 เท่าของอนุกรมดั้งเดิม ความสัมพันธ์เหล่านี้สามารถแสดงด้วยพีชคณิตเล็กน้อย ไม่ว่า "ผลบวก" ของอนุกรมนี้จะเป็นอะไร เรียกมันว่า c = 1 + 2 + 3 + 4 + ⋯ แล้วคูณสมการนี้ด้วย 4 และลบสมการที่สองออกจากสมการแรก จะได้
วิจารณญาณสำคัญอย่างที่สอง คือ อนุกรมสลับ 1 − 2 + 3 − 4 + · · · เป็นการกระจายอนุกรมกำลังรูปนัยของฟังก์ชัน 1/(1 + x)2 โดย 1 เข้าแทนที่ x ดังนั้น รามานุจันเขียนว่า
หารด้วย −3 ทั้งสองข้าง จะได้ว่า c = −1/12
กล่าวโดยทั่วไป เป็นการอันตรายที่จะจัดรูปอนุกรมอนันต์ราวกับเป็นผลบวกจำกัด และอันตรายเป็นพิเศษสำหรับอนุกรมลู่ออก หากแทรกศูนย์เข้าไปในตำแหน่งคงค่าของอนุกรมลู่ออกหนึ่ง ก็เป็นไปได้ที่จะได้ผลออกมาไม่ต้องกันกับตัวเอง (not self-consistent) ไม่ต้องกล่าวถึงความต้องกับวิธีอื่นเลย โดยเฉพาะอย่างยิ่ง ขั้น 4c = 0 + 4 + 0 + 8 + · · · ไม่เพียงแต่ให้เหตุผลโดยกฎเอกลักษณ์การบวกอย่างเดียว สำหรับตัวอย่างแบบสุดโต่ง การเพิ่มศูนย์ตัวเดียวเข้าไปหน้าอนุกรมนี้อาจนำไปสู่ผลที่ไม่ต้องกันได้ทีเดียว[9]
ทางหนึ่งที่จะแก้ไขสถานการณ์นี้ และเพื่อบังคับตำแหน่งที่อาจแทรกศูนย์เข้าไป คือ การติดตามแต่ละพจน์ในอนุกรมโดยการติดตัวไม่อิสระ (dependence) ในบางฟังก์ชัน[10] ในอนุกรม 1 + 2 + 3 + 4 + · · · แต่ละพจน์ n เป็นเพียงจำนวน หากพจน์ n ถูกกำหนดใหม่เป็นฟังก์ชัน n−s โดยที่ s เป็นตัวแปรเชิงซ้อน ก็จะสามารถประกันได้ว่ามีเฉพาะพจน์ประเภทเดียวกันเท่านั้นที่จะถูกเพิ่ม อนุกรมอันเป็นผลนี้อาจเปลี่ยนรูปในทำนองที่เคร่งครัดกว่า และตัวแปร s สามารถตั้งเป็น −1 ได้ทีหลัง การนำยุทธศาสตร์นี้ไปปฏิบัติเรียก การทำให้ปรกติของฟังก์ชันซีตา
อ้างอิง[แก้]
- ↑ Lepowsky, J. (1999). "Vertex operator algebras and the zeta function". ใน Naihuan Jing and Kailash C. Misra (บ.ก.). Recent Developments in Quantum Affine Algebras and Related Topics. Contemporary Mathematics. Vol. 248. pp. 327–340. arXiv:math/9909178. Bibcode:1999math......9178L..
- ↑ Gannon, Terry (April 2010), Moonshine Beyond the Monster: The Bridge Connecting Algebra, Modular Forms and Physics, Cambridge University Press, p. 140, ISBN 978-0521141888.
- ↑ Pengelley, David J. (2002). "The bridge between the continuous and the discrete via original sources". ใน Otto Bekken; และคณะ (บ.ก.). Study the Masters: The Abel-Fauvel Conference. National Center for Mathematics Education, University of Gothenburg, Sweden. p. 3. ISBN 978-9185143009..
- ↑ Hardy p.10
- ↑ Ramanujan's Notebooks, สืบค้นเมื่อ January 26, 2014
- ↑ Abdi, Wazir Hasan (1992), Toils and triumphs of Srinivasa Ramanujan, the man and the mathematician, National, p. 41
- ↑ Berndt, Bruce C. (1985), Ramanujan’s Notebooks: Part 1, Springer-Verlag, pp. 135–136
- ↑ Euler, Leonhard; Lucas Willis; and Thomas J Osler (2006). "Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series". The Euler Archive. สืบค้นเมื่อ 2007-03-22.
{{cite web}}: CS1 maint: multiple names: authors list (ลิงก์) Originally published as Euler, Leonhard (1768). "Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques". Memoires de l'academie des sciences de Berlin. 17: 83–106. - ↑ Tao, Terence (April 10, 2010), The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation, สืบค้นเมื่อ January 30, 2014
- ↑ Promoting numbers to functions is identified as one of two broad classes of summation methods, including Abel and Borel summation, by Knopp, Konrad (1990) [1922]. Theory and Application of Infinite Series. Dover. pp. 475–476. ISBN 0-486-66165-2.




