อัตราส่วนทอง
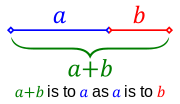
อัตราส่วนทองคำ[1] (อังกฤษ: golden ratio) ในทางคณิตศาสตร์และศิลปะนั้น เลขสองจำนวน (สมมุติให้เป็น a, b และ a>b) จะเป็น "อัตราส่วนทอง" ถ้าอัตราส่วนระหว่างจำนวนมาก (a) ต่อผลรวม (a + b) มีค่าเท่ากับอัตราส่วนระหว่างจำนวนน้อย (b) ต่อจำนวนมาก (a)
"อัตราส่วนทองคำ" เป็นค่าคงที่ทางคณิตศาสตร์ที่ไม่มีเหตุผลชัดเจน มีค่าประมาณ 1.6180339887[2] ชื่ออื่นที่เป็นที่รู้จักของ "อัตราส่วนทองคำ" ในภาษาอังกฤษได้แก่ golden section (ละติน: sectio aurea) และ golden mean[3][4][5], extreme and mean ratio[6], medial section, divine proportion, divine section (ละติน: sectio divina), golden proportion, golden cut[7], golden number, และ mean of Phidias[8][9][10] อัตราส่วนทองคำมักจะแทนด้วยตัวอักษรกรีก "ฟาย" (φ)
โดยค่านี้จะเป็นอัตราส่วนระหว่างค่าของลำดับฟีโบนัชชี 2 ค่า เช่น 610:987 => 1 : 1.618

1. สร้างรูปสี่เหลี่ยมจัตุรัส (สีเหลี่ยมสีแดง)
2. ลากเส้นจากจุดกึ่งกลางของด้านหนึ่งไปยังมุมมุมหนึ่ง
3. ใช้เส้นดังกล่าวเป็นเส้นรัศมีเพื่อสร้างเส้นโค้งและกำหนดเป็นด้านยาวของสี่เหลี่ยมมุมฉาก
อัตราส่วนทองคำในวิธีการเขียนต่าง ๆ[แก้]
เลขฐานสอง : 1.1001111000110111011...
เลขฐานสิบ : 1.6180339887498948482...
เลขฐานสิบหก : 1.9E3779B97F4A7C15F39...
รากไม่รู้จบ :
เศษส่วนไม่รู้จบ :
การเขียนในรูปแบบพีชคณิต :
อ้างอิง[แก้]
- ↑ ศัพท์บัญญัติ ราชบัณฑิตยสถาน เก็บถาวร 2017-07-15 ที่ เวย์แบ็กแมชชีน (สืบค้นออนไลน์)
- ↑ The golden ratio can be derived by the quadratic formula, by starting with the first number as 1, then solving for 2nd number x, where the ratios (x + 1)/x = x/1 or (multiplying by x) yields: x + 1 = x2, or thus a quadratic equation: x2 − x − 1 = 0. Then, by the quadratic formula, for positive x = (−b + √(b2 − 4ac))/(2a) with a = 1, b = −1, c = −1, the solution for x is: (−(−1) + √((−1)2 − 4·1·(−1)))/(2·1) or (1 + √(5))/2.
- ↑ Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5.
- ↑ Piotr Sadowski, The Knight on His Quest: Symbolic Patterns of Transition in Sir Gawain and the Green Knight, Cranbury NJ: Associated University Presses, 1996
- ↑ Richard A Dunlap, The Golden Ratio and Fibonacci Numbers, World Scientific Publishing, 1997
- ↑ Euclid, Elements, Book 6, Definition 3.
- ↑ Summerson John, Heavenly Mansions: And Other Essays on Architecture (New York: W.W. Norton, 1963) p. 37. "And the same applies in architecture, to the rectangles representing these and other ratios (e.g. the 'golden cut'). The sole value of these ratios is that they are intellectually fruitful and suggest the rhythms of modular design."
- ↑ Jay Hambidge, Dynamic Symmetry: The Greek Vase, New Haven CT: Yale University Press, 1920
- ↑ William Lidwell, Kritina Holden, Jill Butler, Universal Principles of Design: A Cross-Disciplinary Reference, Gloucester MA: Rockport Publishers, 2003
- ↑ Pacioli, Luca. De divina proportione, Luca Paganinem de Paganinus de Brescia (Antonio Capella) 1509, Venice.
ดูเพิ่ม[แก้]
แหล่งข้อมูลอื่น[แก้]
- ฟี (Phi) อัตราส่วนทองคำ (Golden ratio) จาก วิชาการ.คอม โดย ดร.ณัฐพันธุ์ ศุภกา
- goldennumber





