ปัญหาการไหลมากสุด
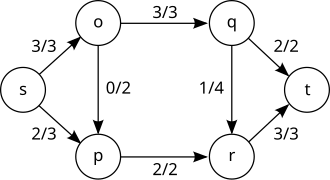
ปัญหาการไหลมากสุด เป็นปัญหาเกี่ยวกับการไหลในเครือข่ายที่ต้องการหาการไหล (เส้นทางน้ำไหน; flow) ซึ่งจะทำให้น้ำที่ไหลออกจากแหล่งต้นทาง (source) ผ่านท่อต่าง ๆ ไปยังแหล่งปลายทาง (sink) มีปริมาณมากที่สุด
ปัญหานี้อาจจะนับเป็นกรณีพิเศษของปัญหาการไหลหมุนเวียนที่ซับซ้อนยิ่งกว่า มีทฤษฎีบทที่สำคัญมากมายเกี่ยวกับปัญหาดังกล่าว หนึ่งในทฤษฎีบทที่เป็นที่รู้จักมากที่สุดคือทฤษฎีบทการไหลมากสุด-คัทต่ำสุดซึ่งกล่าวไว้ว่าปริมาณการไหลที่มากที่สุด (ซึ่งก็คือคำตอบของปัญหาการไหลมากสุด) จะเท่ากับคัทที่ต่ำที่สุด
ประวัติ
[แก้]ส่วนนี้รอเพิ่มเติมข้อมูล คุณสามารถช่วยเพิ่มข้อมูลส่วนนี้ได้ |
นิยามปัญหา
[แก้]ส่วนนี้รอเพิ่มเติมข้อมูล คุณสามารถช่วยเพิ่มข้อมูลส่วนนี้ได้ |
วิธีแก้ไขปัญหา
[แก้]ส่วนนี้รอเพิ่มเติมข้อมูล คุณสามารถช่วยเพิ่มข้อมูลส่วนนี้ได้ |
ทฤษฎีบท
[แก้]ทฤษฎีบทการไหลมากสุด-คัทต่ำสุด
[แก้]ทฤษฎีบทการไหลมากสุด-คัทต่ำสุด กล่าวไว้ว่าปริมาณการไหลที่มากที่สุด จะเท่ากับคัทที่ต่ำที่สุด ทฤษฎีบทนี้ยังเป็นฐานให้กับทฤษฎีบทอีกมากมายเช่นทฤษฎีบทเมนเกอร์
ทฤษฎีบทการไหลที่เป็นจำนวนเต็ม
[แก้]ทฤษฎีบทการไหลที่เป็นจำนวนเต็ม กล่าวไว้ว่าถ้าท่อทั้งหมดมีความจุเป็นจำนวนเต็ม คำตอบของปัญหาการไหลมากสุดก็จะเป็นจำนวนเต็มด้วย
การนำไปใช้
[แก้]ปัญหาการไหลมากสุดหลายแหล่งต้นทาง หลายแหล่งปลายทาง
[แก้]ส่วนนี้รอเพิ่มเติมข้อมูล คุณสามารถช่วยเพิ่มข้อมูลส่วนนี้ได้ |
ปัญหาการจับคู่มากสุด
[แก้]ส่วนนี้รอเพิ่มเติมข้อมูล คุณสามารถช่วยเพิ่มข้อมูลส่วนนี้ได้ |
ปัญหาการไหลมากสุดโดยจุดยอดมีความจุ
[แก้]ส่วนนี้รอเพิ่มเติมข้อมูล คุณสามารถช่วยเพิ่มข้อมูลส่วนนี้ได้ |
