มุมชั่วโมง
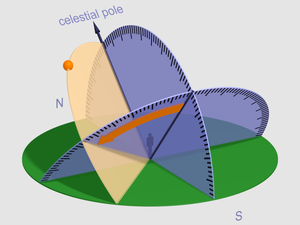
มุมชั่วโมง (อังกฤษ: hour angle) เป็นศัพท์ทางดาราศาสตร์ มุมชั่วโมงของเทห์ฟากฟ้าหมายถึงความแตกต่างระหว่างไรต์แอสเซนชันของเทห์ฟากฟ้า กับเวลาดาราคติในทางดาราศาสตร์และการเดินเรือดาราศาสตร์ มุมชั่วโมงเป็นหนึ่งในพิกัดที่ใช้ใน ระบบพิกัดศูนย์สูตร เพื่อระบุทิศทางของจุดบนทรงกลมท้องฟ้า มุมชั่วโมงของจุดบนทรงกลมท้องฟ้าคือมุมระหว่างระนาบสองระนาบ: ระนาบหนึ่งคือระนาบที่ประกอบด้วยแกนหมุนของโลกและจุดจอมฟ้า (ระนาบเมริเดียน) และอีกระนาบหนึ่งคือระนาบที่ประกอบด้วยแกนหมุนของโลกกับจุดนั้น
มุมชั่วโมงถูกกำหนดโดยเส้นเมริเดียนโดยเป็นลบทางด้านตะวันออกของเส้นเมอริเดียน และเป็นบวกทางด้านตะวันตกของเส้นเมริเดียน หรือนับจากทางตะวันตกไปเรื่อย ๆ เป็นบวกจนถึง 360 องศา วิธีการแปลงมุมชั่วโมงและลองจิจูดคือ 24h = 360°
มุมชั่วโมงถูกนิยามในทางดาราศาสตร์เป็นระยะทางเชิงมุมจากเส้นเมริเดียนตามเส้นศูนย์สูตรท้องฟ้าถึงวงกลมใหญ่บนพื้นผิวทรงกลมที่วัตถุเป้าหมายผ่านขั้วของโลก ระยะทางเชิงมุมควรคำนวณจากทิศตะวันตก[1] หน่วยที่ใช้อาจเป็นชั่วโมง องศา หรือ เรเดียน
ในด้านการเดินเรือดาราศาสตร์ ตามธรรมเนียมแล้วจะยึดตามเส้นเมริเดียนแรก เป็นมุมชั่วโมงเกรนิช (Greenwich hour angle, GHA) หรือเส้นเมอริเดียนท้องถิ่น เป็นมุมชั่วโมงท้องถิ่น (local hour angle, LHA) หรือคำนวณตามต้นยุคอ้างอิง เป็นมุมชั่วโมงดาราคติ (sidereal hour angle, SHA)
มุมชั่วโมงใช้ร่วมกับเดคลิเนชันเพื่อกำหนดพิกัดของจุดบนทรงกลมท้องฟ้าในระบบพิกัดศูนย์สูตรอย่างเที่ยงตรง[2]
ความสัมพันธ์ระหว่างมุมชั่วโมงกับไรต์แอสเซนชัน
[แก้]มุมชั่วโมงท้องถิ่น คำนวณได้โดย
โดยที่ คือเวลาดาราคติท้องถิ่น และ คือไรต์แอสเซนชัน
หรืออาจคำนวณโดย
โดยที่ คือ เวลาดาราคติเกรนิช (Greenwich sidereal time) หมายถึงเวลาดาราคติท้องถิ่นที่เกรนิช ส่วน คือลองจิจูดของผู้สังเกตการณ์ (นับจากเส้นเมริเดียนแรกโดยทิศตะวันออกเป็นค่าบวก)[3]
ถ้ามุมชั่วโมงเป็นค่าลบ (−180° < < 0°) แสดงว่าวัตถุกำลังเข้าใกล้เส้นเมริเดียน และมุมชั่วโมงเป็นบวก (0° < < 180°) แสดงว่าวัตถุกำลังเคลื่อนออกจากเส้นเมริเดียน เมื่อมุมชั่วโมงเป็น 0 แสดงว่าวัตถุอยู่บนเส้นเมริเดียน
นอกจากนี้แล้ว มุมชั่วโมงและมุมไรต์แอสเซนชันมักจะวัดเป็นชั่วโมง นาที และวินาที โดยไม่ใช้ค่าติดลบ การหมุนครบรอบ เทียบเท่ากับ สามารถแปลงไปมากันได้
อ้างอิง
[แก้]- ↑ U.S. Naval Observatory Nautical Almanac Office (1992). P. Kenneth Seidelmann (บ.ก.). Explanatory Supplement to the Astronomical Almanac. Mill Valley, CA: University Science Books. p. 729. ISBN 0-935702-68-7.
- ↑ Explanatory Supplement (1992), p. 724.
- ↑ Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. p. 88. ISBN 0-943396-35-2.









