จำนวนกาตาล็อง
จำนวนกาตาล็อง (อังกฤษ: Catalan numbers) ในคณิตศาสตร์เชิงการจัด ปรากฏอยู่ในปัญหาการนับหลายๆ ปัญหา โดยส่วนใหญ่มักอยู่ในรูปการเรียกซ้ำ (recursive) จำนวนกาตาล็องถูกตั้งชื่อตามชื่อของเออแฌน ชาร์ล กาตาล็อง นักคณิตศาสตร์ชาวฝรั่งเศสและเบลเยียม
จำนวนกาตาล็องตัวที่ n สามารถหาได้โดยใช้สูตรสัมประสิทธิ์ทวินาม ดังนี้
จำนวนกาตาล็องเมื่อ n = 0, 1, 2, 3, … คือ
- 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, … (ลำดับ
 A000108)
A000108)
คุณสมบัติ
[แก้]Cn สามารถเขียนอีกแบบได้
ซึ่งแสดงให้เห็นว่า Cn เป็นจำนวนธรรมชาติ
จำนวนกาตาล็อง เขียนในรูปความสัมพันธ์เวียนเกิด ได้ดังนี้
หรือเขียนอีกแบบได้
จำนวนกาตาล็องมีค่าประมาณ
การประยุกต์ใช้
[แก้]- Cn คือจำนวนของ Dyck word ที่มีความยาว 2n. Dyck word คือ ข้อความที่ประกอบด้วย X และ Y อย่างละ n ตัว และเมื่ออ่านข้อความจากทางซ้ายทีละตัวอักษร จะไม่มีทางนับจำนวนตัว Y ได้มากกว่าตัว X. ตัวอย่าง Dyck words ที่มีความยาว 6
- Cn คือจำนวนวงเล็บ n คู่ทั้งหมดที่อยู่ในลำดับที่ถูกต้อง
- Cn คือจำนวนต้นไม้ทวิภาค (binary tree) ที่มีใบ n + 1 ใบทั้งหมดที่เป็นไปได้

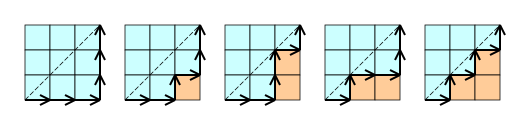
- Cn คือ จำนวนวิถีทางเดียว (monotonic path) ทั้งหมดบนตารางขนาด n × n ช่อง ที่ไม่ตัดเส้นทแยงมุม. วิถีทางเดียว คือ เส้นทางที่เริ่มจากมุมล่างซ้าย และจบที่มุมบนขวา โดยเส้นเชื่อมจะชี้ไปทางขวา หรือข้างบนได้เท่านั้น. ตัวอย่างกรณี n = 3:
- Cn คือจำนวนวิธีตัดรูปหลายเหลี่ยมที่มี n + 2 ด้านให้เป็นรูปสามเหลี่ยม โดยการตัดจะตัดจากจุดยอดของรูป และตัดเป็นเส้นตรง. ตัวอย่าง กรณี n = 4:

ประวัติ
[แก้]ลำดับกาตาล็องถูกค้นพบตั้งแต่คริสต์ศตวรรษที่ 18 โดยเลออนฮาร์ด ออยเลอร์ ซึ่งเขาสนใจจำนวนวิธีตัดรูปหลายเหลี่ยมเป็นรูปสามเหลี่ยม. ลำดับนี้ถูกตั้งชื่อโดย Eugène Charles Catalan เขาได้ค้นพบว่าจำนวนกาตาล็องมีความเกี่ยวข้องกับจำนวนวงเล็บทั้งหมดที่เป็นไปได้
อ้างอิง
[แก้]- Stanley, R.P. (1999): Enumerative Combinatorics, Vol. 2. Cambridge University Press. (pp. 219-229)




![{\displaystyle \sum _{i_{1}+\cdots +i_{m}=n,i_{1},\ldots ,i_{m}\geq 0}C_{i_{1}}\cdots C_{i_{m}}={\begin{cases}{\dfrac {m(n+1)(n+2)\cdots (n+m/2-1)}{2(n+m/2+2)(n+m/2+3)\cdots (n+m)}}C_{n+m/2},&m{\text{ even}}\\[5pt]{\dfrac {m(n+1)(n+2)\cdots (n+(m-1)/2)}{(n+(m+3)/2)(n+(m+3)/2+1)\cdots (n+m)}}C_{n+(m-1)/2},&m{\text{ odd}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05ddd432cab2f6540162cd434b8e22521bbc64a2)

