ความฉลาดแบบกลุ่ม

จากวิกิพีเดีย สารานุกรมเสรี
ภาพแสดงระยะห่างแบบเมตริก (ซ้าย) เทียบกับระยะห่างเชิงลำดับ (ขวา) ของฝูงปลา ปลาจะเกิดปฏิสัมพันธ์แบบไหนขึ้นอยู่กับระยะห่างในแบบเมตริก แต่ในเชิงลำดับ ปฏิสัมพันธ์จะเกิดขึ้นกับปลาจำนวนหนึ่งรอบๆ โดยไม่สนขอบเขตระยะห่าง

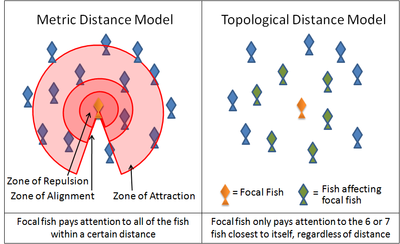
ความฉลาดแบบกลุ่ม (Swarm Intelligence) คือกลุ่มพฤติกรรมของระบบแบบกระจายศูนย์ซึ่งถูกนำมาประยุกต์ใช้ในด้านปัญญาประดิษฐ์ ระบบความฉลาดแบบกลุ่มโดยปกติแล้วจะประกอบขึ้นมาด้วย เอเจนต์ ซึ่งสามารถมีปฏิสัมพันธ์กับเอเจนต์ตัวอื่นหรือสภาวะแวดล้อมได้ เอเจนต์ในระบบทุกตัวจะปฏิบัติตัวตามกฎชุดหนึ่ง แม้ว่าจะไม่มีศูนย์สั่งการที่ควบคุมว่าเอเจนต์แต่ละตัวต้องปฏิบัติอย่างไร แต่การที่เอเจนต์แต่ละตัวมีปฏิสัมพันธ์กันก็ก่อให้เกิดรูปแบบความฉลาดในภาพรวมขึ้นมาซึ่งเอเจนต์แต่ละตัวไม่รู้ แรงบันดาลใจที่ช่วยผลักดันความฉลาดแบบกลุ่มนั้นมักจะมาจากธรรมชาติ โดยเฉพาะจากระบบนิเวศวิทยา ตัวอย่างของความฉลาดแบบกลุ่มที่มาจากธรรมชาติได้แก่ ขั้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยระบบอาณาจักรมด (Ant colony optimization), ขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบกลุ่มอนุภาค (Particle Swarm Optimization), ขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบนกดุเหว่า (Cuckoo search)

เนื้อหา

[แก้] ตัวอย่างความฉลาดแบบกลุ่ม

[แก้] ขั้นตอนวิธีระบบที่มีการเสียสละ

นักวิจัยจากประเทศสวิตเซอร์แลนด์ได้พัฒนาขั้นตอนวิธีขึ้นมาบนพื้นฐานของกฎของฮามิลทันว่าด้วยการเลือกเพื่อดำรงเผ่าพันธ์ (Hamilton's rule of kin selection) ขั้นตอนวิธีนี้ได้แสดงให้เห็นว่าการเสียสละในกลุ่มนั้นจะช่วยให้กลุ่มเจริญเติบโตและมีประสิทธิภาพสูงขึ้นในภาพรวม[1][2]

[แก้] ขั้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยระบบอาณาจักรมด

ขั้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยระบบอาณาจักรมด (Ant colony optimization) นั้นเป็นขั้นตอนวิธีสำหรับหาค่าเหมาะสมที่สุด (Optimization algorithm) ที่มีพื้นฐานมาจากระบบอาณาจักรมด ขั้นตอนวิธีนี้เหมาะที่จะนำไปใช้แก้ปัญหาในการหาเส้นทางไปยังจุดหมายที่ต้องการ มดจำลอง (เทียบได้กับเอเจนต์) จะหาเส้นทางโดยการเคลื่อนที่ผ่านปริภูมิพรารามิเตอร์ (Parameter space) ซึ่งเป็นเซตที่เก็บวิธีการทุกแบบที่เป็นไปได้ไว้ นอกจากการเคลื่อนที่ปกติแล้ว มดจำลองจะบันทึกเส้นทางที่ตัวเองเดินผ่านเอาไว้เหมือนมดในธรรมชาติที่จะปล่อยฟีโรโมนออกมาในระหว่างเดินทางเพื่อนำทางมดตัวอื่นด้วย การบันทึกเส้นทางนี้ช่วยให้มดจำลองสามารถหาคำตอบที่ดีกว่าเดิมได้เมื่อเวลาผ่านไป[3]

[แก้] ระบบภูมิต้านทานประดิษฐ์

ระบบภูมิต้านทานประดิษฐ์ (Artificial immune system) ศึกษาเกี่ยวกับการนำโครงสร้างและหน้าที่ของระบบภูมิคุ้มกันมาปรับใช้ในด้านคอมพิวเตอร์เพื่อแก้ปัญหาคณิตศาสตร์ วิศวกรรม และเทคโนโลยีสารสนเทศ

[แก้] ขั้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยระบบที่มีประจุ

ขั้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยระบบที่มีประจุ (Charged system search) คือขั้นตอนวิธีหาค่าเหมาะสมที่สุดที่สร้างขึ้นมาจากการนำกฎพื้นฐานของฟิสิกส์และกลศาสตร์บางข้อมาปรับใช้งาน[4] ระบบนี้จะจำลองสภาพแวดล้อมที่เอเจนต์เป็นอนุภาคที่มีประจุ ซึ่งจะมีปฎิสัมพันธ์กันในรูปของการดูดและการผลัก ขั้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยระบบที่มีประจุนี้เหมาะกับการนำไปใช้ในการหาค่าเหมาะสมที่สุด โดยเฉพาะเมื่อข้อมูลนำเข้าไม่ลู่ออก

[แก้] ขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบนกดุเหว่า

ขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบนกดุเหว่า (Cuckoo search) เลียนแบบพฤติกรรมการฝากลูกให้คนอื่นเลี้ยงของนกดุเหว่าในแต่ละรุ่น มาปรับใช้ในการค้นหาคำตอบที่ต้องการ การศึกษาเร็วๆ นี้พบว่า CS ทำงานได้เร็วกว่าขั้นตอนวิธีอื่นอย่างเช่น PSO[5]

[แก้] ขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบหิ่งห้อย

ขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบหิ่งห้อย (Firefly algorithm) เป็นอีกหนึ่งขั้นตอนวิธีความฉลาดแบบกลุ่มที่ได้แรงบันดาลใจมาจากพฤติกรรมการเปล่งแสงของหิ่งห้อย ความเข้มของแสงจะผูกกับความน่าดึงดูดของตัวหิ่งห้อย ซึ่งทำให้หิ่งห้อยตัวรอบๆ บินเข้าไปหา ก่อเกิดเป็นกลุ่มย่อยๆ ดังนั้นขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบหิ่งห้อยนี้จึงค่อนข้างเหมาะกับโจทย์ปัญหาหาค่าเหมาะสมที่สุดที่มีผลเฉลยหลายแบบ[6] แต่ก็สามารถนำไปประยุกต์กับปัญหาหาค่าเหมาสมที่สุดที่ข้อมูลนำเข้าเป็นค่าต่อเนื่องเช่นปัญหาการเดินทางของพนักงานขาย (Travelling Salesman Problem)

[แก้] ขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบโน้มถ่วง

ขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบโน้มถ่วง (Gravitational search algorithm) นั้นมีลักษณะคล้ายๆ กับขั้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยระบบที่มีประจุ โดยแตกต่างกันที่ขั้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยระบบที่มีประจุจะใช้กฎด้านไฟฟ้า ส่วนขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบโน้มถ่วงจะใช้กฎด้านแรงโน้มถ่วง เอเจนต์แต่ละตัวจะมีมวลต่างกัน ซึ่งเมื่อเสี้ยวเวลาผ่านไป เอเจนต์แต่ละตัวก็จะดึงดูดซึ่งกันและกัน ทำให้ระบบเคลื่อนที่ไป

[แก้] ขั้นตอนวิธีหาเส้นทางน้ำไหลที่เหมาะสม

ขั้นตอนวิธีหาเส้นทางน้ำไหลที่เหมาะสม (Intelligent Water Drops) คือขั้นตอนวิธีหาค่าเหมาะสมที่สุดโดยใช้ความฉลาดแบบกลุ่มซึ่งได้รับแรงบันดาลใจมาจากการไหลของน้ำในแม่น้ำที่จะเลือกเส้นทางการไหลที่ดีที่สุดเสมอ เอเจนต์แต่ละตัวจะมีปฏิสัมพันธ์กันเหมืนหยดน้ำในแม่น้ำ ซึ่งจะทำให้ได้ผลเฉลยที่ดีขึ้นเรื่อยๆ เมื่อเวลาผ่านไป ขั้นตอนวิธีหาเส้นทางน้ำไหลที่เหมาะสมนี้เป็นขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบเพิ่มพูนและอิงประชากร[7]

[แก้] พลศาสตร์การก่อตัวของลำน้ำ

พลศาสตร์การก่อตัวของลำน้ำ (River formation dynamics)[8] คือวิธีการแบบฮิวริสติกที่คล้ายคลึงกับขั้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยระบบอาณาจักรมด หรืออาจกล่าวได้ว่าพลศาสตร์การก่อตัวของลำน้ำคือขั้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยระบบอาณาจักรมดที่ค่าต่างๆ ไล่ระดับได้ แนวคิดของวิธีการนี้ได้มาจากการกัดเซาะผืนดินของแม่น้ำในระหว่างการก่อตัว วิธีการนี้ยังได้ถูกนำไปใช้ในการแก้ปัญหาเอ็นพีบริบูรณ์หลายๆ อย่างเช่น ปัญหาการค้นหาต้นไม้แผ่กว้างน้อยที่สุดบนกราฟที่มีน้ำหนักแปรผันได้

[แก้] ขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบกลุ่มอนุภาค

ขั้นตอนวิธีหาค่าเหมาะสมที่สุดแบบกลุ่มอนุภาค (Particle Swarm Optimization) เป็นขั้นตอนวิธีหาค่าเหมาะสมที่สุดที่ใช้ได้กับทุกปัญหาที่ผลเฉลยสามารถแทนด้วยจุดหรือระนาบบนปริภูมิขนาด n มิติ เอเจนต์จะถูกวางไว้ในปริภูมิพร้อมกับความเร็วต้นค่าหนึ่งและช่องทางในการติดต่อกับเอเจนท์อื่น[9][10] เอเจนต์จะเคลื่อนที่ไปเรื่อยๆบนปริภูมิผลเฉลย โดยถ้าเอเจนต์ตัวใดเข้าใกล้ผลเฉลยก็จะยิ่งมีความสำคัญมากขึ้น ดึงดูดให้เอเจนต์ตัวอื่นๆ ค่อยๆ เบนเส้นทางมาทางเดียวกัน ข้อดีหลักของขั้นตอนวิธีนี้ต่อขั้นตอนวิธีอื่นที่ใช้ได้กับทุกปัญหาคือขั้นตอนวิธีนี้สามารถหลีกเลี่ยงปัญหาค่าเหมาะสมที่สุดสัมพัทธ์ (Local minima) ได้จากการที่สามารถมีจำนวนเอเจนต์เยอะ

[แก้] ขั้้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยการแพร่เชิงสุ่ม

ขั้้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยการแพร่เชิงสุ่ม (Stochastic diffusion search) คือขั้นตอนวิธีหาค่าเหมาะสมที่สุดที่อาศัยความน่าจะเป็นในการแก้โจทย์ปัญหาประเภทที่ฟังก์ชั่นค่านำเข้าสามารถแยกย่อยเป็นฟังก์ชั่นย่อยๆ ได้ เอเจนต์แต่ละตัวจะมีสมมติฐานของตัวเองว่าผลลัพธ์ใดถูกต้อง ซึ่งสมมติฐานนี้จะถูกทดสอบเรื่อยๆ โดยนำเป้าหมายยย่อยมาพิจารณา ในขั้นตอนวิธีแบบมาตราฐาน ฟังก์ชั่นย่อยแต่ละตัวสามารถให้ผลการทดสอบที่เป็นจริงหรือเท็จเท่านั้น ทำให้เอเจนต์แต่ละตัวมี 2 สถานะคือสถานะทำงานและสถานะไม่ทำงาน ข้อมูลของสมมติฐานจะถูกส่งผ่านไปยังเอเจนต์ตัวอื่นในแบบเดียวกับการแพร่ ขั้้นตอนวิธีหาค่าเหมาะสมที่สุดด้วยการแพร่เชิงสุ่มถือเป็นขั้นตอนวิธีที่มีประสิทธิภาพสูงในด้านการหาค่าเหมาะสมที่สุดตัวหนึ่ง

[แก้] การประยุกต์ใช้

ขั้นตอนวิธีความฉลาดแบบกลุ่มต่างๆ นั้นสามารถนำมาประยุกต์ได้หลากหลาย เช่นการจำลองกลุ่มคนในภาพยนต์ หรือการค้นหาเส้นทางในระบบสื่อสารโดยใช้การเคลื่อนที่แบบมด (อังกฤษ: Ant-based routing) เป็นต้น

ไฟล์:Battle of Helm's Deep.jpg
ภาพฉากสงครามจากภาพยนตร์ไตรภาคเดอะลอร์ดออฟเดอะริงส์

[แก้] การจำลองกลุ่มคน

การจำลองกลุ่มคน (Crowd simulation) คือหนึ่งในวิธีที่ผู้ผลิตภาพยนต์นิยมใช้ในการสร้างฉากที่มีฝูงชนจำนวนมาก หนึ่งในตัวอย่างที่เด่นชัดคือฉากสงครามในภาพยนตร์ไตรภาคเดอะลอร์ดออฟเดอะริงส์ ที่ใช้เทคโนโลยีการจำลองเข้าช่วยในการสร้างฉากที่ดูสมจริง ความฉลาดแบบกลุ่มมักถูกเลือกไปใช้กับงานประเภทนี้เพราะสามารถทำได้ง่าย

[แก้] การค้นหาเส้นทางในระบบสื่อสารโดยใช้การเคลื่อนที่แบบมด

นอกเหนือจากการนำความฉลาดแบบกลุ่มไปใช้ในการแก้ปัญหาหาค่าเหมาะสมที่สุดแล้ว ความฉลาดแบบกลุ่มยังได้ถูกนำมาใช้กับระบบสื่อสารโทรคมนาคมอีกด้วย โดยนำระบบการค้นหาเส้นทางโดยใช้การเคลื่อนที่แบบมด (อังกฤษ: Ant-based routing) ไปใช้ในการหาเส้นทางที่ดีที่สุดในระบบจริงที่ไม่รู้ค่านำเข้า (Input) โดยระบบจะปล่อยเอเจนต์รูปแบบมดให้ท่องไปในระบบเน็ตเวิร์ค

[แก้] อ้างอิง

  1. ^ Altruism helps swarming robots fly better genevalunch.com, 4 May 2011.
  2. ^ Waibel M, Floreano1 D and Keller L (2011) "A quantitative test of Hamilton's rule for the evolution of altruism" PLoS Biology, 9(5): e1000615. doi:10.1371/journal.pbio.1000615
  3. ^ Ant Colony Optimization by Marco Dorigo and Thomas Stützle, MIT Press, 2004. ISBN 0-262-04219-3
  4. ^ Kaveh, A.; Talatahari, S. (2010). "A Novel Heuristic Optimization Method: Charged System Search". Acta Mechanica 213 (ฉบับที่ 3-4): 267–289. doi:10.1007/s00707-009-0270-4. 
  5. ^ P. Civicioglu and E. Besdok, A conception comparison of the cuckoo search, particle swarm optimization, differential evolution and artificial bee colony algorithms, Artificial Intelligence Review, DOI 10.1007/s10462-011-92760, 6 July (2011).
  6. ^ Yang X. S., (2008). Nature-Inspired Metaheuristic Algorithms. Frome: Luniver Press. ISBN 1905986106.
  7. ^ Shah-Hosseini, Hamed (2009). "The intelligent water drops algorithm: a nature-inspired swarm-based optimization algorithm". International Journal of Bio-Inspired Computation 1 (ฉบับที่ 1/2): 71–79. http://www.inderscience.com/filter.php?aid=22775. 
  8. ^ Using River Formation Dynamics to Design Heuristic Algorithms by Pablo Rabanal, Ismael Rodríguez and Fernando Rubio, Springer, 2007. ISBN 978-3-540-73553-3
  9. ^ Parsopoulos, K. E.; Vrahatis, M. N. (2002). "Recent Approaches to Global Optimization Problems Through Particle Swarm Optimization". Natural Computing 1 (ฉบับที่ 2-3): 235–306. doi:10.1023/A:1016568309421. 
  10. ^ Particle Swarm Optimization by Maurice Clerc, ISTE, ISBN 1-905209-04-5, 2006.

[แก้] แหล่งข้อมูลอื่น

ดึงข้อมูลจาก "http://th.wikipedia.org/w/index.php?title=ความฉลาดแบบกลุ่ม&oldid=3482174".
เครื่องมือส่วนตัว

สิ่งที่แตกต่าง
การกระทำ
ป้ายบอกทาง
มีส่วนร่วม
พิมพ์/ส่งออก
เครื่องมือ
ภาษาอื่น