ปัญหาการแบ่งจัตุรัสเป็นจัตุรัส
ปัญหาการแบ่งจัตุรัสเป็นจัตุรัส (อังกฤษ: Squaring the square) เป็นปัญหาทางเรขาคณิต โดยให้แบ่งสี่เหลี่ยมจัตุรัสที่มีความยาวด้านเป็นจำนวนเต็ม ให้เป็นสี่เหลี่ยมจัตุรัสย่อยที่มีความยาวด้านเป็นจำนวนเต็ม ถ้าสี่เหลี่ยมจัตุรัสย่อยเหล่านั้นมีความยาวด้านแตกต่างกันทั้งหมด จะเรียกว่าเป็น "การแบ่งจัตุรัสเป็นจัตุรัสอย่างสมบูรณ์"
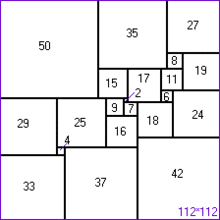
การแบ่งจัตุรัสเป็นจัตุรัสอย่างสมบูรณ์[แก้]
A. J. W. Duijvestijn ใช้คอมพิวเตอร์ในการค้นหาคำตอบของปัญหานี้ และพบคำตอบที่แบ่งเป็นสี่เหลี่ยมจัตุรัส 21 รูป และได้พิสูจน์ว่าเป็นจำนวนรูปที่น้อยที่สุดที่สามารถแบ่งได้
อ้างอิง[แก้]
- Brooks, R. L.; Smith, C. A. B.; Stone, A. H.; and Tutte, W. T. The Dissection of Rectangles into Squares, Duke Math. J. 7, 312-340, 1940
- Martin Gardner, "Squaring the square," in The 2nd Scientific American Book of Mathematical Puzzles and Diversions.
- C. J. Bouwkamp and A. J. W. Duijvestijn, Catalogue of Simple Perfect Squared Squares of Orders 21 Through 25, Eindhoven Univ. Technology, Dept. of Math., Report 92-WSK-03, Nov. 1992.
- C.J.Bouwkamp and A.J.W.Duijvestijn, Album of Simple Perfect Squared Squares of order 26, Eindhoven University of Technology, Faculty of Mathematics and Computing Science, EUT Report 94-WSK-02, December 1994.
แหล่งข้อมูลอื่น[แก้]
- http://www.squaring.net
- http://www.maa.org/editorial/mathgames/mathgames_12_01_03.html
- http://www.math.uwaterloo.ca/navigation/ideas/articles/honsberger2/index.shtml เก็บถาวร 2015-10-16 ที่ เวย์แบ็กแมชชีน
- http://www.math.niu.edu/~rusin/known-math/98/square_dissect เก็บถาวร 2003-04-19 ที่ เวย์แบ็กแมชชีน
- http://www.stat.ualberta.ca/people/schmu/preprints/sq.pdf เก็บถาวร 2015-09-24 ที่ เวย์แบ็กแมชชีน
- http://karl.kiwi.gen.nz/prosqtre.html เก็บถาวร 2012-07-16 ที่ เวย์แบ็กแมชชีน
- http://karl.kiwi.gen.nz/prosqtsq.html เก็บถาวร 2015-10-14 ที่ เวย์แบ็กแมชชีน
