การเรนเดอร์ภาพด้วยคอมพิวเตอร์

ตัวอย่างการให้แสงและเงา ของอาคาร 3 มิติในคอมพิวเตอร์ คำนวณผลออกมาดังรูป

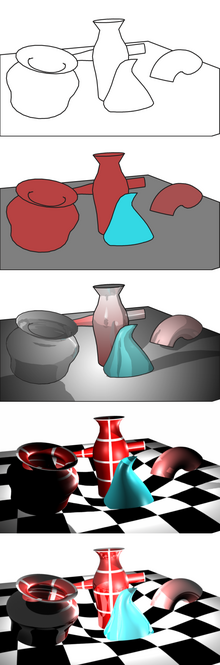
การเรนเดอร์ภาพด้วยคอมพิวเตอร์ หรือ เรนเดอร์ริง (อังกฤษ: rendering) ยังคงเรียกว่า "การสร้างภาพจากแบบจำลอง" หรือ "การสร้างเป็นภาพสุดท้าย" คือกระบวนการสร้างภาพสองมิติจากแบบจำลองกราฟิกในระบบ โดยเริ่มจากการนำเข้าแบบจำลองกราฟิกซึ่งจะบรรยายวัตถุสองมิติ หรือสามมิติโดยบอกโครงสร้างข้อมูลของวัตถุสามมิติ อันประกอบด้วยข้อมูลเชิงเรขาคณิต ได้แก่พิกัด มุมมอง พื้นผิวลวดลาย และข้อมูลเกี่ยวกับความสว่าง และคำนวณเพื่อแสดงผลลัพธ์เป็นภาพสองมิติบนจอ ซึ่งจะเป็นภาพแบบดิจิทัล (ภาพเชิงเลข) หรือ ภาพแบบจุดภาพ (ภาพแรสเตอร์) ทั้งนี้การเรนเดอร์ภาพไม่ได้จำกัดอยู่เฉพาะการให้แสงและเงา ในบางกรณีก็หมายถึงการให้สี หรือการให้เส้น โดยไม่ต้องมีการให้แสงเงาก็ได้

หลักการทำงาน

ในการให้แสงและเงาการเรนเดอร์จะทำการคำนวณค่าสี และความสว่าง ณ ตำแหน่งต่าง ๆ บนแบบจำลอง โดยใช้หลักการคำนวณหาจุดตกกระทบของแสงจากแหล่งกำเนิด หลังจากนั้นจึงเข้าสู่กระบวนการสร้างให้เป็นจุดภาพหรือ แรสเตอไรเซชั่น (Rasterization)ซึ่งจะเป็นการฉาย (Project)แบบจำลองลงบนระนาบสองมิติ ก่อนส่งค่าไปแสดงบนจอภาพ กระบวนการนี้เป็นขั้นตอนสุดท้ายในสายท่อกราฟิก หรือ กราฟิกไปป์ไลน์ (Graphic Pipeline)โดยจะให้ผลลัพธ์เป็นการแสดงรูปหรือการเคลื่อนไหวที่สร้างขึ้น

ความเป็นมา

ในทางคอมพิวเตอร์กราฟิกกระบวนการสร้างภาพจากแบบจำลองเริ่มเป็นประเด็นสำคัญในการศึกษาตั้งแต่ยุค 1970 เนื่องจากความซับซ้อนของเรขภาพคอมพิวเตอร์ โดยกระบวนการนี้มีความสำคัญในแง่ต่าง ๆ เช่น คอมพิวเตอร์เกม การจำลอง เทคนิคพิเศษทางภาพยนตร์หรือโทรทัศน์ และ การออกแบบการสร้างภาพมโนทัศน์ ส่วนซอฟต์แวร์สำเร็จรูปบ้างก็รวมเข้ากระบวนการนี้กับซอฟต์แวร์สำหรับสร้างแบบจำลอง และสร้างแอนิเมชัน บ้างก็แยกเป็นซอฟต์แวร์เฉพาะต่างหาก อีกทั้งยังสามารถหาได้ในรูปแบบของซอฟต์แวร์ไม่จำกัดลิขสิทธิ์ ซึ่งขั้นตอนของการสร้างตัวเรนเดอร์ หรือ ตัวสร้างภาพจากแบบจำลองนั้นอาศัยการรวมศาสตร์ต่าง ๆ หลายแขนงเช่น ฟิสิกส์ของแสง การรับรู้ด้านการมองเห็น คณิตศาสตร์ และ วิศวกรรมซอฟต์แวร์

กรณีของกราฟิกส์สามมิติ การสร้างภาพจากแบบจำลองนั้นเป็นกระบวนการที่ทำได้ช้า และกินเวลาในการคำนวณมาก (เช่นขั้นตอนการสร้างภาพยนตร์) ซึ่งสามารถใช้กราฟิกฮาร์ดแวร์เร่งความเร็วการประมวลผลสามมิติแบบทันกาลเข้าช่วยได้ (เช่นการเพิ่มความเร็วของเกม) ซึ่งคำภาษาอังกฤษว่า"เรนเดอร์"ได้มาจากศัพท์ที่หมายถึงขั้นตอนการลงแสงและเงาภาพของศิลปินหรือ หรือ อาร์ทิส เรนเดอริ่ง (Artist Rendering)แต่ในทางคอมพิวเตอร์กราฟิกขั้นตอนนี้กินความกว้างกว่าดังที่ได้อธิบายไว้

การเรนเดอร์แบบไบแอส (Biased) และ อันไบแอส (Unbiased)

โดยทั่วไปซอฟต์แวร์ที่ใช้ในงานเรนเดอร์จะแบ่งเป็นสองกลุ่มหลัก ได้แก่กลุ่มที่ใช้เทคนิคการเรนเดอร์แบบไบแอส (biased) และแบบอันไบแอส (unbiased) โดยในกลุ่มที่เรียกว่า unbiased จะมีการคำนวณแสงที่ซับซ้อนและใช้เวลานานกว่ากลุ่ม biased และเป็นที่นิยมในการใช้เรนเดอร์ภาพนิ่ง ลักษณะของซอฟต์แวร์ในกลุ่มนี้คือยิ่งให้เวลามาก ภาพก็ยิ่งออกมาดูสมจริง ส่วนกลุ่ม biased นิยมใช้สำหรับการเรนเดอร์ภาพเคลื่อนไหวเพราะกินเวลาน้อยกว่ามากในแต่ละเฟรม และให้ผลที่ค่อนข้างดี เทคนิคที่สำคัญในกลุ่มนี้เช่น photon mapping นอกจากนี้ การเรนเดอร์แบบ biased ยังอาจเปิดช่องให้ผู้สร้างงานบิดเบือนความจริงเพื่อประโยชน์ในเชิงศิลปะได้ง่ายกว่าแบบ unbiased ที่กระบวนการต่างๆล้วนมีเพื่อสร้างภาพให้สมจริงถึงที่สุด จะอย่างไรก็ดี ซอฟต์แวร์สำหรับเรนเดอร์บางตัวก็มีคุณลักษณะจากทั้งสองกลุ่มเทคนิค ดังนั้นการทำความเข้าใจลักษณะเฉพาะของเทคนิคต่างๆจะช่วยให้ผู้สร้างงานสามารถเลือกปรับแต่งคุณลักษณะของซอฟต์แวร์ให้ทำงานตรงตามความต้องการและตรงต่อเวลาได้มากที่สุด และอยู่เหนือแนวคิดที่ว่าจะต้องเลือกใช้การเรนเดอร์ภาพแบบ biased หรือ unbiased

เรนเดอร์ฟาร์ม (Render farm)

การเรนเดอร์ภาพที่ซับซ้อนมากๆหรือภาพเคลื่อนไหวจะกินเวลานานกว่าภาพที่มีองค์ประกอบง่ายๆหรือภาพเดี่ยวๆ ซอฟต์แวร์ที่ใช้ในการเรนเดอร์จึงอาจได้รับการออกแบบเพิ่มเติมมาเพื่อให้สามารถแบ่งงานให้กับคอมพิวเตอร์หลายเครื่องหรือเครื่องเดียวแต่หลายหน่วยประมวลผลกลาง (CPU) ช่วยกันเรนเดอร์เพื่อให้งานเสร็จเร็วยิ่งขึ้น การแบ่งงานนี้อาจเป็นการแบ่งภาพเดียวออกเป็นภาพเล็กๆแล้วกระจายงานให้แต่ละหน่วยประมวลผล ซึ่งเหมาะกับการเรนเดอร์ภาพนิ่ง หรืออาจแบ่งออกเป็นช่วงเวลาหรือเฟรมสำหรับงานแอนิเมชัน มักเรียกกลุ่มของคอมพิวเตอร์หลายๆเครื่องที่ช่วยกันเรนเดอร์ภาพว่าเรนเดอร์ฟาร์ม (render farm)

rendering equation

rendering equation อธิบายถึงจำนวนของแสงที่ออกจากจุด x ไปยังมุมมองหนึ่งๆ

$L_o(x, \vec w) = L_e(x, \vec w) + \int_\Omega f_r(x, \vec w', \vec w) L_i(x, \vec w') (\vec w' \cdot \vec n) d\vec w'$

ในตำแหน่งและทิศทางหนึ่งๆ แสงขาออก หรือ outgoing light (L_o) จะเท่ากับผลรวมของแสงที่ถูกปล่อย หรือ emit (L_e) กับที่ถูกสะท้อนออกมา โดยแสงที่ถูกสะท้อนออกมาคือผลรวมของผลคูณแสงขาเข้า หรือ incoming light (L_i) จากทุกทิศทางกับการสะท้อนของพื้นผิว (bidirectional reflectance distribution function) และมุมขาเข้า

ดูเพิ่ม

• Global illumination
• Diffuse reflection
• Specular reflection