องศา (มุม)

บทความนี้เกี่ยวกับองศาของมุม สำหรับความหมายอื่น ดูที่ องศา (แก้ความกำกวม)

องศา
ข้อมูลทั่วไป
ระบบการวัด	หน่วยที่ยอมรับให้ใช้แก่ระบบเอสไอ
เป็นหน่วยของ	มุม
สัญลักษณ์	° หรือ deg
การแปลงหน่วย
1 ° ใน ...	... มีค่าเท่ากับ ...
รอบ	1/360 รอบ
เรเดียน	π/180 rad ≈ 0.01745.. rad
มิลลิเรเดียน	50·π/9 mrad ≈ 17.45.. mrad
แกร็ด	10/9g

1 องศา (สีแดง) และ 89 องศา (สีน้ำเงิน)

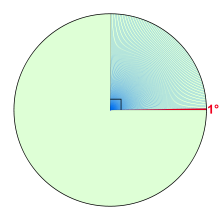
องศา (อังกฤษ: degree) หรือในชื่อเต็มคือ ดีกรีของส่วนโค้ง (อังกฤษ: degree of arc, arcdegree) คือหน่วยวัดมุมชนิดหนึ่งบนระนาบสองมิติ หนึ่งองศา แทนการกวาดมุมรอบจุดศูนย์กลางของวงกลมไปได้ 1 ส่วนใน 360 ส่วน และเมื่อมุมนั้นอ้างอิงกับเส้นเมอริเดียน องศาจะแสดงให้เห็นถึงตำแหน่งต่างๆ บนวงกลมใหญ่ของทรงกลม อย่างที่มีการใช้อ้างอิงตำแหน่งบนโลก ดาวอังคาร หรือทรงกลมท้องฟ้า เป็นต้น สัญลักษณ์วงกลมเล็ก ° ใช้แทนหน่วยองศาในการเขียน และเป็นหน่วยเดียวที่ไม่ต้องเว้นวรรคระหว่างตัวเลขกับสัญลักษณ์ เช่น

ในทางคณิตศาสตร์ มุมที่วัดเป็นหน่วยองศามีที่ใช้น้อย เนื่องจากความสะดวกในการหารเลข 360 ได้ลงตัวนั้นไม่สำคัญ นักคณิตศาสตร์นิยมใช้หน่วยเรเดียน (radian) เป็นแบบฉบับด้วยเหตุผลที่หลากหลาย ในระบบนี้มุมที่มีขนาด 180° และ π เรเดียน จะมีค่าเท่ากันหรือเทียบเท่ากัน ดังนั้น 1° จึงมีขนาดเท่ากับ π/180 เรเดียน นั่นหมายความว่าจำนวนองศาภายในวงกลม (360°) จะมีค่าเท่ากับ 2π เรเดียน และเส้นรอบวงของวงกลมก็จะมีขนาดเท่ากับ 2πr โดยที่ r คือความยาวของรัศมี

ในการคิดค้นระบบเมตริก ซึ่งอยู่บนพื้นฐานของเลขยกกำลังของ 10 ได้มีการพยายามที่จะนิยาม "องศาฐานสิบ" ที่เรียกว่า แกร็ด (grad) ใช้หน่วยเป็น ก็อน (gon) ดังนั้นจำนวนของแกร็ดในมุมฉากจะมีขนาด 100 ก็อน และมีทั้งหมด 400 ก็อนในวงกลม ถึงแม้ว่าแนวความคิดนี้จะไม่ได้รับแรงผลักดัน แต่เครื่องคิดเลขทางวิทยาศาสตร์ยังคงรองรับระบบแกร็ดอยู่

มิล (angular mil) คือมุมที่มีขนาดเป็น 1/1000 ของเรเดียน ซึ่งเป็นหน่วยที่ใช้สะดวกในการสำรวจและการประมาณระยะทางของวิศวกรโดยใช้ตรีโกณมิติอย่างง่าย

ในเกมคอมพิวเตอร์ที่มีการสร้างโลกเสมือนจริงในสามมิติ ความต้องการการประมวลผลที่รวดเร็วส่งผลให้เกิดการยอมรับเลขฐานสองเข้ามาใช้วัดมุม ระบบที่ใช้กันจะมี 256 องศาในวงกลม ดังนั้นมุมฉากจึงมีขนาดเท่ากับ 64 องศา โดยค่าของมุมจะถูกเก็บในที่ว่างขนาด 1 ไบต์ และสำหรับฟังก์ชันตรีโกณมิติที่ถูกเรียกใช้ จะเอาไปเทียบกับค่าในตารางผลลัพธ์ที่กำหนดไว้แล้ว (ไม่ต้องคำนวณ) ในขณะนี้ยังไม่มีชื่อเฉพาะของหน่วยดังกล่าว

ดูเพิ่ม

• ลิปดา
• เรเดียน

แหล่งข้อมูลอื่น

• องศาในนิยามของการวัดมุม พร้อมแสดงแอนิเมชัน (อังกฤษ)