รูปสี่เหลี่ยมคางหมู
| รูปสี่เหลี่ยมคางหมู | |
|---|---|
 รูปสี่เหลี่ยมคางหมูรูปหนึ่ง | |
| ชนิด | รูปสี่เหลี่ยม |
| ขอบและจุดยอด | 4 |
| พื้นที่ | |
| สมบัติ | รูปหลายเหลี่ยมนูน |
ในทางเรขาคณิต รูปสี่เหลี่ยมคางหมู คือรูปสี่เหลี่ยมชนิดหนึ่งที่มีด้านตรงข้ามขนานกันจำนวนหนึ่งคู่ รูปสี่เหลี่ยมคางหมู ABCD เขียนแทนด้วยสัญลักษณ์ที่สำเนียงอังกฤษและออสเตรเลียเรียกว่า trapezoid [1][2]
นิยาม[แก้]
มีข้อถกเถียงกันเกี่ยวกับจำนวนด้านที่ขนานกันในรูปสี่เหลี่ยมคางหมู ปัญหาอยู่ที่ว่ารูปสี่เหลี่ยมด้านขนานซึ่งมีด้านขนานกันสองคู่ควรจัดเป็นรูปสี่เหลี่ยมคางหมูหรือไม่ ผู้แต่งตำรากลุ่มหนึ่ง [3] นิยามว่ารูปสี่เหลี่ยมคางหมูเป็นรูปสี่เหลี่ยมที่มีด้านขนานกัน เพียงหนึ่งคู่เท่านั้น โดยไม่นำรูปสี่เหลี่ยมด้านขนานมารวม ราชบัณฑิตยสถานได้ให้นิยามของรูปสี่เหลี่ยมคางหมูไว้ว่า รูปสี่เหลี่ยมคางหมูคือรูปสี่เหลี่ยมด้านขนานที่มีด้านขนานกันเพียงคู่เดียว [4] และพจนานุกรมศัพท์วิทยาศาสตร์ คณิตศาสตร์ และเทคโนโลยี ของสถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี ได้ให้คำนิยามไว้ว่า รูปสี่เหลี่ยมคางหมูคือรูปสี่เหลี่ยมใด ๆ ที่มีด้านตรงข้ามขนานกันคู่หนึ่ง และคู่เดียวเท่านั้น [5]
ผู้แต่งตำราอีกกลุ่มหนึ่ง [6] นิยามว่ารูปสี่เหลี่ยมคางหมูเป็นรูปสี่เหลี่ยมที่มีด้านขนานกัน อย่างน้อยหนึ่งคู่ ซึ่งทำให้รูปสี่เหลี่ยมด้านขนานเป็นกรณีพิเศษของรูปสี่เหลี่ยมคางหมู (รวมไปถึงรูปสี่เหลี่ยมขนมเปียกปูน รูปสี่เหลี่ยมมุมฉาก รูปสี่เหลี่ยมผืนผ้า และรูปสี่เหลี่ยมจัตุรัสด้วย) นิยามอย่างหลังสอดคล้องกับการใช้งานในคณิตศาสตร์ระดับสูงกว่าเช่นแคลคูลัส แนวคิดการประมาณด้วยหลักเกณฑ์เชิงสี่เหลี่ยมคางหมู (trapezoidal rule) ของปริพันธ์จำกัดเขตจะไม่สมบูรณ์หากใช้นิยามอย่างแรก
พื้นที่[แก้]
พื้นที่ของรูปสี่เหลี่ยมคางหมูใด ๆ สามารถคำนวณได้จาก [6]
เมื่อ a, b คือความยาวของด้านคู่ขนานและ h คือความสูงระหว่างด้านคู่ขนาน เมื่อประมาณ ค.ศ. 499 นักคณิตศาสตร์และนักดาราศาสตร์ชาวอินเดียชื่อ อารยภฏะ ได้ใช้วิธีการคำนวณนี้ในศาสตรนิพนธ์ อารยภฏียะ (ตอนที่ 2.8) [7] สูตรนี้เป็นผลได้มาจากกรณีพิเศษของสูตรพื้นที่รูปสามเหลี่ยมอันเป็นที่รู้จัก โดยพิจารณาว่ารูปสามเหลี่ยมคือภาวะลดรูปของรูปสี่เหลี่ยมคางหมู ซึ่งด้านที่ขนานกันด้านหนึ่งยุบลงจนกลายเป็นจุด
ส่วนของเส้นตรงกึ่งกลางรูปสี่เหลี่ยมคางหมู คือส่วนของเส้นตรงที่เชื่อมระหว่างจุดกึ่งกลางของด้านที่ไม่ขนานกัน ความยาวของส่วนของเส้นตรงนี้ m เท่ากับค่าเฉลี่ยความยาวของด้านคู่ขนานของรูปสี่เหลี่ยมคางหมู
เป็นผลให้พื้นที่ของรูปสี่เหลี่ยมคางหมู เท่ากับความยาวของส่วนของเส้นตรงกึ่งกลางรูปสี่เหลี่ยมคางหมูคูณด้วยความสูง
ถ้าให้ a, b เป็นด้านที่ขนานกันและ c, d เป็นด้านที่ไม่ขนานกัน ในกรณีที่ด้านคู่ขนานยาวไม่เท่ากัน (a ≠ b) จะสามารถคำนวณหาความสูง h ได้จากสูตรนี้
และพื้นที่ของรูปสี่เหลี่ยมคางหมูนี้เท่ากับ
เมื่อด้านคู่ขนานด้านหนึ่งยุบลงจนกลายเป็นจุด (a = 0) สูตรนี้จะลดรูปลงเป็นสูตรของเฮรอนสำหรับคำนวณพื้นที่รูปสามเหลี่ยม
สูตรพื้นที่อีกสูตรหนึ่งที่เทียบเท่า ซึ่งดูคล้ายสูตรของเฮรอนมากกว่าคือ
โดยที่ s คือครึ่งหนึ่งของความยาวรอบรูปของรูปสี่เหลี่ยมคางหมู แม้สูตรนี้จะดูคล้ายสูตรของพรัหมคุปตะแต่ก็มีบางจุดที่ต่างไป เนื่องจากรูปสี่เหลี่ยมคางหมูอาจไม่ใช่รูปสี่เหลี่ยมวงกลมล้อม (บรรจุภายในรูปวงกลมพอดีไม่ได้) สูตรนี้ก็ยังเป็นกรณีพิเศษของสูตรของเบรทชไนเดอร์สำหรับรูปสี่เหลี่ยมทั่วไป
หากใช้สูตรของเบรทชไนเดอร์จะได้
จุดกึ่งกลางของพื้นที่ (ศูนย์กลางมวลของแผ่นเอกรูป) อยู่บนส่วนของเส้นตรงที่เชื่อมโยงระหว่างจุดกึ่งกลางของด้านที่ขนานกัน ในระยะห่างตั้งฉาก d จากด้านที่ยาวกว่า b ดังนี้
สมบัติ[แก้]
- รูปสี่เหลี่ยมคางหมูหน้าจั่ว ซึ่งเป็นรูปสี่เหลี่ยมคางหมูชนิดหนึ่ง มีสมบัติเพิ่มเติมว่ามุมที่ฐานมีขนาดเท่ากัน และด้านที่ไม่ขนานจะยาวเท่ากัน
- รูปสี่เหลี่ยมรูปหนึ่งจะเป็นรูปสี่เหลี่ยมคางหมู ก็ต่อเมื่อมุมที่อยู่ติดกันรวมเป็นมุมประกอบสองมุมฉาก (180 องศา) จำนวนสองคู่ เงื่อนไขอีกอย่างหนึ่งที่สำคัญและเพียงพอคือ เส้นทแยงมุมตัดกันด้วยอัตราส่วนของความยาวเท่ากัน (ค่านี้เป็นค่าเดียวกับอัตราส่วนระหว่างด้านคู่ขนาน)
- เส้นตรงที่ลากผ่านจุดกึ่งกลางของด้านคู่ขนานทั้งสองแบ่งครึ่งพื้นที่ของรูปสี่เหลี่ยมคางหมู

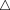 AOD เท่ากับพื้นที่ของ
AOD เท่ากับพื้นที่ของ 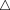 BOC และผลคูณของพื้นที่ระหว่าง
BOC และผลคูณของพื้นที่ระหว่าง 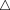 AOD กับ
AOD กับ 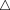 BOC เท่ากับผลคูณของพื้นที่ระหว่าง
BOC เท่ากับผลคูณของพื้นที่ระหว่าง  AOB กับ
AOB กับ  COD อัตราส่วนของพื้นที่ของรูปสามเหลี่ยมแต่ละคู่ที่อยู่ติดกันจะเท่ากับอัตราส่วนของความยาวของด้านคู่ขนาน
COD อัตราส่วนของพื้นที่ของรูปสามเหลี่ยมแต่ละคู่ที่อยู่ติดกันจะเท่ากับอัตราส่วนของความยาวของด้านคู่ขนาน- ความยาวของเส้นทแยงมุม p, q เท่ากับ (a, b คือความยาวของด้านคู่ขนาน)
- กำหนดให้ ABCD เป็นรูปสี่เหลี่ยมคางหมูที่มีจุดยอด A, B, C, D เรียงตามลำดับและมีด้านคู่ขนาน AB กับ DC ; ให้ E เป็นจุดตัดของเส้นทแยงมุม และให้ F กับ G เป็นจุดจุดหนึ่งที่อยู่บนด้าน DA กับ BC ตามลำดับซึ่งทำให้ FEG ขนานกับด้านคู่ขนาน AB กับ DC ; จะได้ว่า FG คือมัชฌิมฮาร์มอนิกของ AB กับ DC นั่นคือ
สถาปัตยกรรม[แก้]

ในสถาปัตยกรรมแบบอียิปต์โบราณ มีการเจาะช่องหน้าต่าง ประตู และการก่อสร้างตัวอาคารเป็นรูปสี่เหลี่ยมคางหมูโดยมีด้านฐานกว้างกว่าด้านยอด
ดูเพิ่ม[แก้]
- polite number หรือในอีกชื่อหนึ่งคือ จำนวนเชิงสี่เหลี่ยมคางหมู
- หลักเกณฑ์เชิงสี่เหลี่ยมคางหมู
อ้างอิง[แก้]
- ↑ "trapezoid". Oxford Dictionaries. April 2010. Oxford University Press. 14 March 2011 <http://oxforddictionaries.com/view/entry/m_en_gb0878690[ลิงก์เสีย]>.
- ↑ "trapezium". Oxford Dictionaries. April 2010. Oxford University Press. 14 March 2011 <http://oxforddictionaries.com/view/entry/m_en_gb0878650[ลิงก์เสีย]>.
- ↑ "American School definition from "math.com"". สืบค้นเมื่อ 2008-04-14.
- ↑ พจนานุกรมราชบัณฑิตยสถาน เก็บถาวร 2009-03-03 ที่ เวย์แบ็กแมชชีน (สืบค้นออนไลน์)
- ↑ ผลการค้นหา สี่เหลี่ยมคางหมู จากพจนานุกรมศัพท์วิทยาศาสตร์ คณิตศาสตร์ และเทคโนโลยี สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี[ลิงก์เสีย] (สืบค้นออนไลน์)
- ↑ 6.0 6.1 เอริก ดับเบิลยู. ไวส์สไตน์, "Trapezoid" จากแมทเวิลด์.
- ↑ Aryabhatiya เก็บถาวร 2011-08-15 ที่ archive.today มราฐี: आर्यभटीय, Mohan Apte, Pune, India, Rajhans Publications, 2009, p.66, ISBN 978-81-7434-480-9
แหล่งข้อมูลอื่น[แก้]
- Trapezoid definition Area of a trapezoid Median of a trapezoid With interactive animations
- Trapezoid (North America) at elsy.at: Animated course (construction, circumference, area)
- [1] on Numerical Methods for Stem Undergraduate
- Autar Kaw and E. Eric Kalu, Numerical Methods with Applications, (2008) [2]














